DSV1_P2_2009_06_08
Werbung
Digitale Signal-Verarbeitung 1
Prüfung 2: 8.6.09
Name:
Zeit: 90 Minuten
Schriftliche Unterlagen und Taschenrechner erlaubt
PC und Handy nicht erlaubt
Jede vollständig richtig gelöste Teilaufgabe gibt 3 Punkte,
wenn nichts anderes angegeben wurde.
Tipps:
Zuerst alle Aufgaben durchlesen und mit der einfachsten beginnen.
Jede Teilaufgabe lässt sich unabhängig von den anderen lösen,
wenn nichts anderes angegeben wurde.
1. Pol-Nullstellen-Darstellung
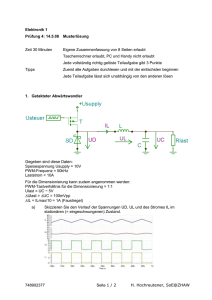
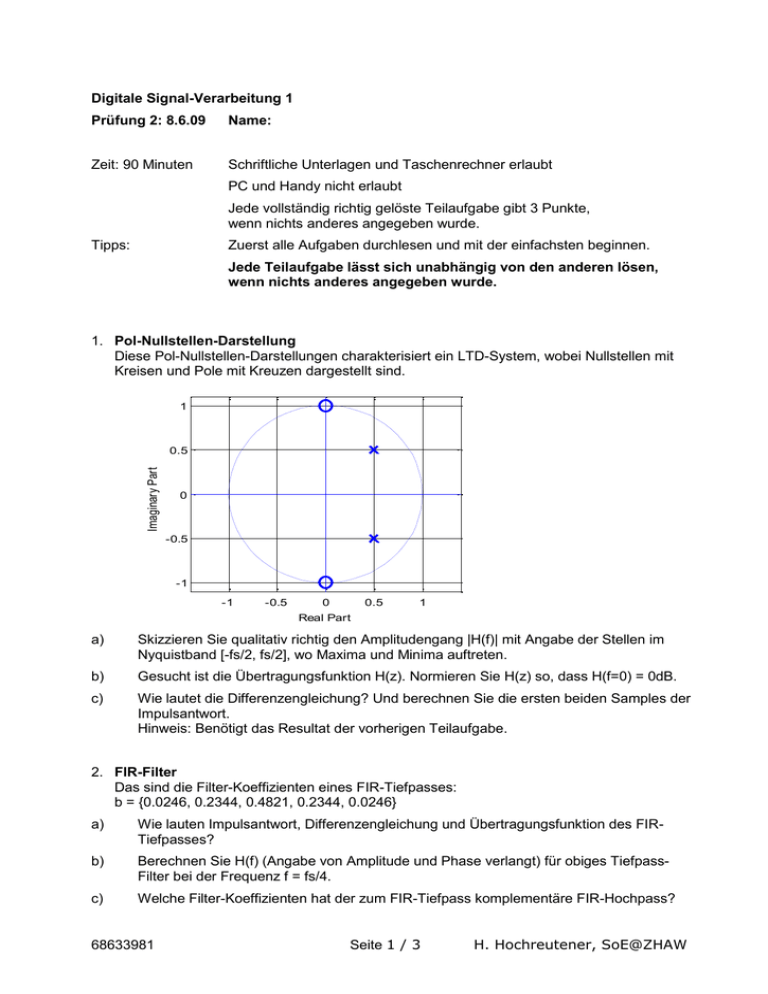
Diese Pol-Nullstellen-Darstellungen charakterisiert ein LTD-System, wobei Nullstellen mit
Kreisen und Pole mit Kreuzen dargestellt sind.
1
Imaginary Part
0.5
0
-0.5
-1
-1
-0.5
0
0.5
1
Real Part
a)
Skizzieren Sie qualitativ richtig den Amplitudengang |H(f)| mit Angabe der Stellen im
Nyquistband [-fs/2, fs/2], wo Maxima und Minima auftreten.
b)
Gesucht ist die Übertragungsfunktion H(z). Normieren Sie H(z) so, dass H(f=0) = 0dB.
c)
Wie lautet die Differenzengleichung? Und berechnen Sie die ersten beiden Samples der
Impulsantwort.
Hinweis: Benötigt das Resultat der vorherigen Teilaufgabe.
2. FIR-Filter
Das sind die Filter-Koeffizienten eines FIR-Tiefpasses:
b = {0.0246, 0.2344, 0.4821, 0.2344, 0.0246}
a)
Wie lauten Impulsantwort, Differenzengleichung und Übertragungsfunktion des FIRTiefpasses?
b)
Berechnen Sie H(f) (Angabe von Amplitude und Phase verlangt) für obiges TiefpassFilter bei der Frequenz f = fs/4.
c)
Welche Filter-Koeffizienten hat der zum FIR-Tiefpass komplementäre FIR-Hochpass?
68633981
Seite 1 / 3
H. Hochreutener, SoE@ZHAW
3. IIR-Filter
a)
Das sind die Filter-Koeffizienten einer IIR-Hochpasses zum Unterdrücken der tiefen
Frequenzen (Netzbrummen: 50Hz-Sperre bei fs = 1000Hz):
b = {0.8203, -2.4439, 2.4439, -0.8203}
a = {-2.6043, 2.2698, -0.6541}
// erster Koeffizient = a1, a0 = 1
Wie müssen die Filter-Koeffizienten skaliert werden, damit sie im Q15-Format dargestellt
werden können?
Um Überlaufen von Zwischenresultaten zu vermeiden soll das Eingangssignal nur mit
1/8 gewichtet in die Berechnungen einfliessen. Das muss auch beim Ausgangssignal
entsprechend berücksichtigt werden.Wie lautet die so modifizierte Differenzengleichung
für die Implementation in der transponierten Direktstruktur II?
b)
Das sind die Filter-Koeffizienten eines IIR-Tiefpasses, der dazu dient die hohen
Frequenzen leicht abzuschwächen, damit man das Rauschen im Signal weniger hört:
b = { 0.4208, 0.4208}
a = {-0.1584}
// erster Koeffizient = a1, a0 = 1
b = { 13789, 13789}
// das Selbe im Q15-Format
a = {-5190}
Weder die Filter-Koeffizienten noch das Eingangs-Signal müssen skaliert werden, da ein
Überlauf sehr unwahrscheinlich ist und der Effekt durch die sättigende Arithmetik
genügend gut abgefangen wird.
Das Filter soll auf dem TI-DSP TMS320C5510 (verwendet im DSV1-Labor) mit Hilfe von
Compiler-Intrinsics (siehe Tabelle unten) implementiert werden.
Schreiben Sie nur den Code-Ausschnitt mit der Filter-Implementation in Direktstruktur II.
c)
Für den Entwurf von IIR-Filtern werden oft analoge Prototypen und die bilineare
Transformation verwendet.
Erklären sie das Verfahren Schritt für Schritt, vom gegebenen Stempel-MatrizenSchema bis zu den gesuchten Filter-Koeffizienten für das digitale System.
d)
Weshalb werden bei der Filter-Realisierung mit Biquads immer die konjugiert komplexen
Pole resp. Nullstellen zu einem Teilfilter zusammengefasst?
68633981
Seite 2 / 3
H. Hochreutener, SoE@ZHAW
4. Windowing und Leakage
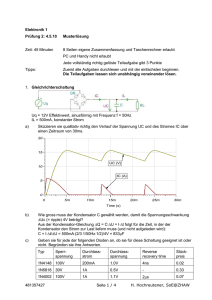
Die Figur zeigt links die Gewichtungs-Faktoren des Hanning-Fensters der Länge 32 und
rechts die Auswirkungen im Frequenzbereich (Frequenzachse: 0 .. fs/2)
Von einem Signal werden 32 Samples erfasst, mit obigem Fenster gewichtet und mittels
FFT das Frequenzspektrum berechnet.
a)
Wie gross ist die Frequenzauflösung f/(fs/2) mit obigem Fenster, wenn Signale mit
20dB unterschiedlicher Amplitude sicher auseinandergehalten werden sollen?
b)
Wie gross wäre die Frequenzauflösung f/(fs/2) der 32-Punkt-FFT alleine? D. h. ohne
Fenster und ohne Leakageeinfluss (= ganzzahlige Anzahl Perioden erfasst).
5. Stempel-Matrizen-Schema
Ein Bandpass soll die Frequenzen von 300Hz bis 3kHz durchlassen. Der Fehler der
Amplitude im Durchlassbereich darf maximal 3dB betragen.
Die Frequenzen unterhalb von 100 Hz und oberhalb von 3.6kHz sollen mit mindestens 40dB
abgeschwächt werden.
Die Samplingfrequenz beträgt 8kHz.
a)
Zeichnen Sie das zugehörige Stempel-Matrizen-Schema und beschriften Sie es mit den
Kennwerten.
b)
Kann das Stempel-Matrizen-Schema auch verwendet werden für die Spezifikation des
Phasenganges? Antwort begründen.
68633981
Seite 3 / 3
H. Hochreutener, SoE@ZHAW