Mechanik für Bachelor plus Aufgabenblatt 10
Werbung

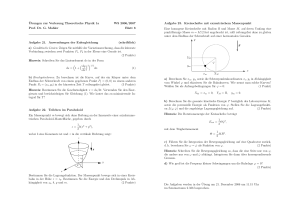
Mechanik für Bachelor plus Ludwig-Maximilians-Universität München Dr. Michael Haack Aufgabenblatt 10 6 Abgabe: 1. Juli 2013 1 MECHANIK 1.4 Seilrollen (F2004) Aufgabe 1: Seilrollen (10 Punkte) Eine Punktmasse m3 hängt an einem EndeEnde eines masselosen Länge,das das über eine Eine Masse m3 hängt an einem eines masselosenSeils Seils fester fester Länge, fixierte, reibungsfreie Scheibereibungsfreie läuft. Am Scheibe anderenläuft. Ende SeilsEnde ist eine masselose über eine fixierte, Amdes anderen des Seils ist eine Scheibe bemasselose Scheibe befestigt, über die einLänge zweitesreibungsfrei masseloses Seil fester festigt,über die ein zweites masseloses Seil fester läuft, an Länge dem wieder zwei reibungsfrei läuft, an dem wieder zwei Massen befestigt sind, nämlich m und die Schwer1 Punktmassen, nämlich m1 und m2 befestigt sind (siehe Figur). Auf alle Massen wirkt m2 (s. Skizze). Auf alle Massen wirkt die Schwerkraft senkrecht nach unten. kraft entlang des Lots (senkrecht nach unten in der Figur). a) Bestimmen Sie die Lagrange-Funktion L(x1 ,L(x x3 ,1ẋ, x1 ,3 ,ẋẋ31), ẋdieses Systems. Sie die (a) Bestimmen Sie die Lagrangefunktion Systems.Beachten Be3 ) dieses achten Sie die Zwangsbedingungen x + x = const. und x + x = const.. 3 1 2 Zwangsbedingungen x + x3 = const., x1 + x2 = const. (10 Punkte) (4 Punkte) b) Bestimmen Sie die Beschleunigung der Masse (b) Bestimmen Sie die Beschleunigung der m Masse 3 . m3 . (4 Punkte) (10 Punkte) (c) Zeigen Sie, daß die Beschleunigung von m3 verschwindet, wenn folgende c) Diskutieren Sie das Ergebnis: Zeigen Sie, dass die Beschleunigung von m 3 verschwindet, Bedingung erfüllt ist: 4m1 m2 wenn folgende Bedingung erfüllt ist: m3 = . (1.1) m1 + m2 4m1 m2 Betrachten Sie nun speziell den Fall Sie qualitativ, warum 1 = m2 . Begründen m3m= . die Beschleunigung von m3 (aus (1.1)) in m diesem Fall verschwindet. (2 Punkte) + m 1 2 Betrachten Sie dabei speziell den Grenzfall m1 = m2 . Begründen Sie qualitativ, warum die Beschleunigung von m3 in diesem Grenzfall verschwindet. (5 Punkte) 1 Aufgabe 2: Massenpunkt auf rotierender Stange∗ (10 Punkte) Wir betrachten einen Massenpunkt der Masse m, der sich längs einer rotierenden Stange bewegen kann (s. Skizze). Die Stange rotiere mit einer konstanten Winkelgeschwindigkeit ω. Außer den dadurch bedingten Zwangskräften sollen keine weiteren Kräfte wirken. Insbesondere soll die Masse reibungsfrei auf der Stange gleiten (vgl. Aufg. 2, Blatt 5). ⇢ Wir wählen den Abstand ρ vom Zentrum als verallgemeinerte Koordinate für den Massenpunkt. (a) Wie lautet der Zusammenhang zwischen den kartesischen Koordinaten x und y mit der verallgemeinerten Koordinate ρ? (2 Punkte) (b) Benutzen Sie diesen Zusammenhang, um die Lagrangefunktion L(ρ, ρ̇) für den Massenpunkt herzuleiten. Wie lautet die Euler-Lagrange Gleichung? (4 Punkte) (c) In der Vorlesung wird gezeigt, daß für ein System, dessen Lagrangefunktion nicht explizit von der Zeit abhängt, d.h. für das ∂L/∂t = 0 gilt, die folgende Größe (die Hamiltonfunktion) eine Erhaltungsgröße ist: H= f X ∂L q̇j − L . ∂ q̇j j=1 (2.1) Dies gilt insbesondere für den Massenpunkt auf der rotierenden Stange. Berechnen Sie H für diesen Fall und zeigen Sie, daß es sich nicht um die Energie des Massenpunktes handelt. (2 Punkte) (d) Benutzen Sie die Bewegungsgleichung aus Teil (b), um explizit zu zeigen, daß das H, das Sie in Teil (c) berechnet haben, erhalten ist. (2 Punkte) Bei Fragen: [email protected] ∗ : Aufgabe wird korrigiert. Die Punkte dienen nur der Orientierung und haben keinerlei praktische Konsequenzen. 2