Trainingsblatt Bestimmung von Potenzfunktionen

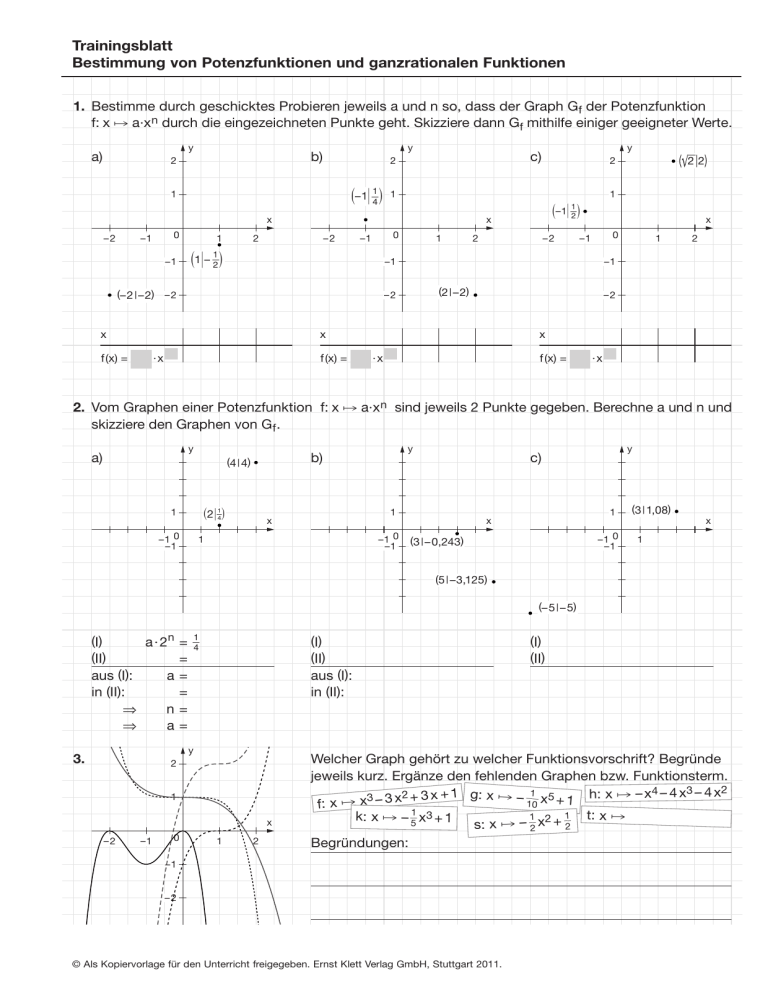
Trainingsblatt
Bestimmung von Potenzfunktionen und ganzrationalen Funktionen
1. Bestimme durch geschicktes Probieren jeweils a und n so, dass der Graph Gf der Potenzfunktion
f: x 哫 a·xn durch die eingezeichneten Punkte geht. Skizziere dann Gf mithilfe einiger geeigneter Werte.
y
a)
y
b)
2
–1 14 1
–2
–1
1
1
–1
1 – 2
–2
0
–1
1
2
–2
x
0
–1
–1
(–2|–2) – 2
(2| –2)
f (x) =
2
–2
x
·x
1
–1
–2
x
f (x) =
–1 1
2
x
1
2
2 2
2
1
x
0
y
c)
2
x
·x
3
f(x) =
·x
2. Vom Graphen einer Potenzfunktion f: x 哫 a·xn sind jeweils 2 Punkte gegeben. Berechne a und n und
skizziere den Graphen von Gf .
y
a)
2 14
1
–1 0
–1
y
b)
(4 | 4)
1
x
–1 0
–1
1
y
c)
1
x
–1 0
–1
1
(3|–0,243
)
(3| 1,08)
x
1
(5|–3,125)
(–5| –5)
(I)
a ·2n =
(II)
=
aus (I):
a=
in (II):
=
⇒
n=
⇒
a=
1
4
(I)
(II)
aus (I):
in (II):
y
3.
2
1
x
–2
–1
0
1
2
(I)
(II)
Welcher Graph gehört zu welcher Funktionsvorschrift? Begründe
jeweils kurz. Ergänze den fehlenden Graphen bzw. Funktionsterm.
2
3
4
3 – 3 x2 + 3 x + 1 g: x 哫 – 1 x5 + 1 h: x 哫 – x – 4 x – 4 x
x
哫
1
0
x
f:
t: x 哫
1 2 1
k: x 哫 – 51 x3 + 1
s: x 哫 – 2 x + 2
Begründungen:
–1
–2
© Als Kopiervorlage für den Unterricht freigegeben. Ernst Klett Verlag GmbH, Stuttgart 2011.