8.) Ringbeschleuniger-Resonatoren (cavities)

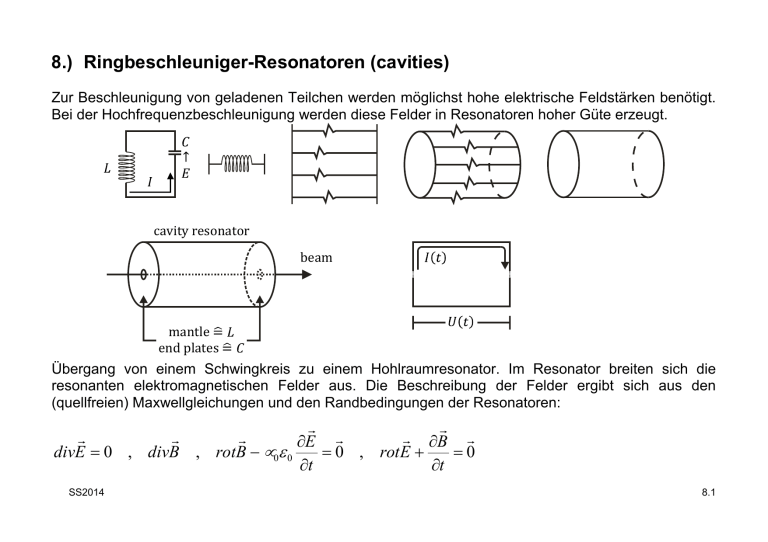
8.) Ringbeschleuniger-Resonatoren (cavities)
Zur Beschleunigung von geladenen Teilchen werden möglichst hohe elektrische Feldstärken benötigt.
Bei der Hochfrequenzbeschleunigung werden diese Felder in Resonatoren hoher Güte erzeugt.
cavity resonator
beam
mantle
end plates
Übergang von einem Schwingkreis zu einem Hohlraumresonator. Im Resonator breiten sich die
resonanten elektromagnetischen Felder aus. Die Beschreibung der Felder ergibt sich aus den
(quellfreien) Maxwellgleichungen und den Randbedingungen der Resonatoren:
r
r
r
r
r
r
r
∂E
∂B r
divE = 0 , divB , rotB − µ0ε 0
= 0 , rotE +
=0
∂t
∂t
SS2014
8.1
r
r r
∂
rot rotB − µ0ε 0 rotE = 0 ⇒
∂t
Ebenso erhält man
r
2
r
r
∂ B r
grad divB − ∆B + µ0ε 0 2 = 0
∂t
r
r
∂2B r
∆B − µ0ε 0 2 = 0
∂t
r
2
r
∂ E r
∆E − µ0ε 0 2 = 0
∂t
(7.1)
1
Außerdem gilt µ0ε 0 = c 2
r r
r r − iωt
r r
r r − iωt
Mit E ( r , t ) = E ( r )e
und B ( r , t ) = B ( r )e
erhält man
r
r
r ω 2 ∂2B r
r ω 2 ∂2E r
∆B − 2 2 = 0 und ∆E − 2
=0
c ∂t
c ∂t 2
Wir teilen nun den Laplaceoperator in einen transversalen und einen longitudinalen Teil auf
∂2
∂2
∂2
∆ = 2 + 2 + 2 = ∇ t2 + ∇ l2
∂x
∂y
∂z
SS2014
dann kann man mit folgendem Ansatz weiterrechnen
8.2
r r
r
E (r ) = E ( x, y )e ± ikz
und
r r
 2 ω2
2
 ∇ t + 2 − k  B = 0
c


r r
r
B(r ) = B( x, y )e ± ikz
und
r r
 2 ω2
2
 ∇ t + 2 − k  E = 0
c


(7.2)
Die speziellen Lösungen ergeben sich aus der Art des Resonators und den Randbedingungen. Diese
Randbedingungen sind:
r
E||
r
E
E|| würde Ladungen verschieben und für E|| = 0 sorgen
r r r
Daher E × n = 0
r
r E⊥
n
r
B||
SS2014
r
B
r
r B⊥
n
B┴ würde über Induktion für einen Strom sorgen, der
Diese Komponente kompensieren würde
r r r
Daher folgt B ⋅ n = 0
8.3
Bei HF-Systemen kommt noch der Skineffekt hinzu. Dieser begrenzt die Tiefe im Metall, indem die
Ströme an der Oberfläche fließen können. Die theoretische Ableitung ergibt eine Diffusionsgleichung
für die Stromdichte entlang der Oberfläche und damit ein exponentieller Abfall der Stromdichte mit
zunehmender Tiefe im Metall. Die Größe, welche den exponentiellen Abfall bestimmt ist die Skintiefe
δ=
2ρR
ωµ 0 µ r
(7.3)
ist die Feldeindringtiefe in den Leiter mit endlichen spezifischen ohmschen Widerstand ρ R
Beispiel:
Kupfer ( ρ Cu = 1.8 ⋅ 10 −8 Ωm) und ω ≈ 108 Hz → δ ≈ 10 µm
Im Allgemeinen betrachtet man nun zwei Resonatorgeometrien, den Rechteckresonator und den
Zylinderresonator:
SS2014
8.4
Bei den Lösungen unterscheidet man H-Wellen und E-Wellen.
E-Welle
B-Welle
E z ≠ 0 , d.h. B hat nur transversale Komponenten --> TM-Mode
B z ≠ 0 , d.h. E hat nur transversale Komponenten --> TE-Mode
Der einfachste Hohlraumresonator ist der Topfkreis (pill box cavity). Dieser zylindrische
Hohlraumresonator entsteht durch den Abschluss eines zylinderförmigen Wellenleiters. Die für die
Hochfrequenzbeschleunigung wichtigste Schwingungsform ist die TM010 Mode. TMnmq bedeutet n
azimutale Perioden, m radiale Knoten und q halbe Perioden in longitudinaler Richtung. Mit der
Grundwelle TM010 erhalten wir die Felder:
a
iω t
′
B
=
0
,
B
=
0
,
B
=
−
i
E
J
(
k
r
)
e
ω
Eφ = 0 , Er = 0 , E z = E0 J 0 (k01r )e
r
φ
0 0
01
und z
(7.4)
x01c 2
Nun gelten J 0′ (k01r ) = − J1 (k01r ) und x01 = 2,40483 ist die Nullstelle J 0 ( x01 ) = 0
iω t
Die Resonanzfrequenz ist durch den Innenradius a und diese Nullstelle bestimmt
ν=
2,40483 ⋅ c
(7.5)
2π a
Bsp. für einen Innenradius
von 0,23 m ergibt sich
ν = 500 MHz
SS2014
8.5
Die Länge der Kavität kann bei dieser Mode nahezu frei gewählt werden. Die Teilchen werden in der
Mitte maximal beschleunigt, da das longitudinale elektrische Feld Ez für r = 0 maximal ist.
8.1. Ferritkavitäten
Eine interessante Variante ist der Koaxialresonator. Dessen Resonanzfrequenz kann durch die
Änderung der Permeabilität µ der Ferritkerne verändert werden. Das Schema einer SIS18 FerritKavität ist untenstehend dargestellt:
1) Die SIS18-Kavität besteht aus zwei Stapeln von je 32 Ferrit-Scheiben.
2) Die Ferrit-Ringe sind vom Typ Ferroxcube FXC 8C12m (Phillips in Eindhoven).
3) Abmessungen der Ferrit-Scheiben: da=498 mm, di=270 mm, l=25 mm.
4) Die beiden Ferrit-Stapel werden über 6 achtförmige Windungen vorbestromt (Änderung von µ).
SS2014
8.6
5) Die Einkopplung der HF erfolgt gemischt, induktive-und kapazitive Einkopplung.
6) Die Gapspannung jeder Gaphälfte wird über einen Gapspannungsteiler gemessen.
7) Die in die achtförmigen Vorbestromungswindungen eingekoppelte HF wird über 3 Blockkondensatoren von 15x5 nF = 75 nF abgeleitet.
8) Die Gapkapazität ist 250 pF, zusätzlich sind nochmal2x150 pF parallel zum Gap geschaltet.
Zur Ferrit-Füllung der Kavität!
SS2014
8.7
Das Schema der SIS18-Ferritkavität mit Tetrodenverstärker
SS2014
8.8
Ein vereinfachtes Kavitätenmodell zur Auswertung der ersten und zweiten Maxwellschen Gleichung ist
nachfolgend gezeigt:
Kavitätengehäuse mit
keramischem Gap wird durch
eine einzige Windung mit
Gapkapazität vereinfacht
SS2014
8.9
Die Einkoppelschleife (grün) koppelt die HF vom Generator in die Kavität ein. Die achtförmige Schleife
sorgt dafür, dass beide Ringkernstapel fest miteinander verkoppelt werden und die gleiche
Flussrichtung zueinander haben. Nachstehend eine Verdeutlichung der Funktion der Achterschleife.
Die Auswertung der ersten Maxwellschen Gleichung am vereinfachten Kavitätenmodell soll nun
durchgeführt werden. Die Lösungen ergeben sich unter Berücksichtigung der Randbedingung, dass an
den elektrisch leitenden Wänden die elektrischen Feldkomponenten parallel zur Wandoberfläche und
die magnetischen Feldkomponenten senkrecht zur Wandoberfläche verschwinden
SS2014
8.10
Wir wenden nun die erste Maxwellsche Gleichung an
r r
∫ H ⋅ d l =iges
i8
Beim rechten Ringkernstapel ergibt sich
H ϕ 2πr = −iA + is + i8 = 0
iS
Beim linken Stapel ergibt sich
Hϕ 2π r = is − i8 = 0
Zieht man beide Gleichungen voneinander ab so gilt
iA=iHF
oder
iA + 2i8 = 0
i
i8 = A
2
Das heißt, die achtförmige Schleife führt den halben HF-Strom. Für das azimuthale Magnetfeld gilt
Hϕ 2π r = −
iHF
+ is
2
Das kann man benutzen die Gapspannung und die Kavitätenimpedanz auszurechnen:
SS2014
8.11
Die Gapspannung ist mit φ = magnetischer Fluss
r
v r
µ0 µ r lres a
U g = −iω 2 ⋅ Φ = −iω 2 ⋅ ∫ B ⋅ dA = −iω 2
H ϕ dr
∫
2
π
A
ri
= −iω 2
µ0 µ r lres  iHF
  ra 
 
−
+
i

s  ln 
2π  2
  ri 
Dabei sind ra und ri die Radien der Ferritkerne.
Die Resonatorimpedanz ist dann
 i

U g = −2iges ⋅ Z = −2 − HF + is  ⋅ Z
 2

is =
Ug
Zg
⇒ Z res =
Ug
iHF
=
Z
1 + 2 ZZg
oder U g = iHF
Z
1 + 2 ZZg
Gapspannung unter Einfluss des Strahlstroms:
SS2014
8.12
Unter Berücksichtigung des Stroms des Teilchenstrahls,
muss der Gesamtstrom zur Berechnung der Gapspannung
modifiziert werden.

iHF
iHF U g 




U g = −2iω ⋅ Φ = −2 Z  ib −
+ is  = −2 Z  ib −
+
2
2 ZG 



Ug =
2Z
1 + 2 ZZg
 iHF

− ib  = Z Kav ⋅ iHF − 2Z Kav ⋅ ib

 2

Der Strahl entnimmt dem Resonator Leistung und vermindert
dadurch die gap-Spannung. Daher muss mehr HF-Leistung
eingespeist werden --> Beam loading
8.2. Phasenfokussierung und TT
Die HF-Beschleunigung kann nur funktionieren, wenn die Teilchen longitudinal in Pakete (Bunche)
gebündelt sind, ein Auseinanderlaufen der Teilchenpakete verhindert wird und die Synchronisation der
Teilchenpakete mit dem beschleunigenden HF-Feld erhalten bleibt.
Phasenfokussierung
SS2014
8.13
Immer dann, wenn die Teilchen mit unterschiedlichem Impuls unterschiedliche Laufzeiten haben, tritt
die Phasenfokussierung in Erscheinung. Linearbeschleuniger, Synchrozyklotron, Synchrotron und
Mikrotron sind z.B. HF-Beschleuniger mit Phasenfokussierung. Immer dann, wenn auch Teilchen mit
unterschiedlichem Impuls gleiche Laufzeiten (Isochron Modus in Ringen) haben, entfallen die
Notwendigkeit und die Möglichkeit der Phasenfokussierung. Das Isochronzyklotron ist z. B. ein HFBeschleuniger ohne Phasenfokussierung.
Synchronisationsbedingung: ω HF = h ⋅ ωs
wobei ωs die Kreisfrequenz des Teilchens ist und ωHF die HF-Frequenz der Beschleunigungscavities
darstellt. h ist die Harmonische Zahl
Der Fahrplan für die Hochbeschleunigung wird von der Magnetfeldrampe für die Ablenkmagnete
vorgegeben. Aus der Geschwindigkeit, mit der das Magnetfeld der Ablenkmagnete hochgefahren wird,
ergibt sich für das synchrone Teilchen der Energiezuwachs [∆Es]U pro Umlauf.
[∆Es ]U
= Cs
dps
dt
; Cs = Umlauflänge Synchronteilchen
dp s
= q ⋅ R ⋅ B&
dt
C
∆p s = q ⋅ R ⋅ B& τ s = q ⋅ R ⋅ B& ⋅ s
E 2 = p 2 c 2 + m02 c 4 ⇒ ∆E = cβ ⋅ ∆p
cβ
mit p s = q ⋅ R ⋅ B ⇒
SS2014
8.14
dp
∆E = cβ ⋅ ∆p s = q ⋅ R ⋅ B& ⋅ C s = s ⋅ C s
dt
Wir ermitteln nun den Energiegewinn
beim Durchqueren eines
Beschleunigungsspaltes.
Das elektrische Wechselfeld ist
E s (0, s, t ) = E s (0, s) sin(ω HF ⋅ t + ϕ s )
sin (ω HF t + ϕ s )
dps
= qE s (0, s, t ) = qE s (0, s ) sin(ω HF ⋅ t + ϕ s )
dt
Phasendefinition Ringbeschleuniger:
Diese folgt einer Sinusfunktion und
nicht wie bei den Linearbeschleunigern
einer Kosinusfunktion.
D.h. Nullgrad Sollphase ist der Nulldurchgang und nicht wie bei den Linac
Gaps das Maximum der Beschleunigungsspannung.
SS2014
0o
90o
180o
360o
8.15
g/2
∆E
HF
s
=q
g/2
∫ E (0, s) sin(ω
s
HF
−g / 2
⋅ t + ϕ s )ds = q
∫ E (s)[sin(ω
s
HF
⋅ t ) cos ϕ s + cos(ωHF ⋅ t ) sin ϕ s )]ds
−g / 2
g/2
1
E0 =
E s ( s)ds
∫
Mit
folgt
g −g / 2
∆E sHF
g/2
 g/2

E s ( s) cos(ω HF ⋅ t )ds
 ∫ E s ( s) sin(ω HF ⋅ t )ds

∫
−g / 2
−g / 2
 = q ⋅ g ⋅ E T sin ϕ
= q ⋅ g ⋅ E0 
cos
ϕ
+
sin
ϕ
s
s
0
s
g/2
g/2


E s ( s)ds
E s ( s )ds
∫
∫


−g / 2
−g / 2
mit
g/2
 g/2

E s ( s) cos(ω HF ⋅ t )ds 
 ∫ E s ( s) sin(ω HF ⋅ t )ds
∫
−g / 2
−g / 2
 ≤1
T = 
cot
+
ϕ
s
g/2
g/2



E s ( s )ds
E s ( s )ds
∫
∫


−g / 2
−g / 2
SS2014
8.16
Dies ist der sogenannte Transit-Time-Factor (TTF). E0*g ist die durchfallene Spannung für ein
Teilchen, wenn sich das elektrische Feld zeitlich nicht ändert. Der TTF misst das Verhältnis zwischen
dem realen Energiegewinn des Teilchens zu dem in einem dc-Feld mit der Spannung E0 gT sin ϕ s .
Der TTF ist ein Maß für die Reduzierung des Energiegewinns durch das zeitlich variierende elektrische
g/2
Feld im Spalt. Nun gilt
∫ E (s) sin(ω
s
HF
⋅ t )ds = 0
−g / 2
, wenn das Feld symmetrisch zu s=0 ist, denn
sin(ω HF ⋅ t ) ist antimetrisch in s. Damit erhält man für den TTF:
 g/2

 ∫ E s ( s) cos(ω HF ⋅ t )ds 
−g / 2
 ≤1
T = 
g/2



E s ( s )ds
∫


−g / 2
Ist der Geschwindigkeitszuwachs gering, so gilt
ω HF ⋅ t = ω ⋅ ∫
ds
s
2π ⋅ s 2π ⋅ s
=ω⋅
=
=
βλ
v( s )
v( s ) THF βc
βλ ist der Weg, den ein Teilchen mit der Geschwindigkeit β*c in einer HF-Periode zurücklegt.
SS2014
8.17
Damit und für ein konstantes Feld folgt:
g/2
Es 0
T=
∫
cos(
2π ⋅ s
−g / 2
βλ
)ds
Es 0 g
g /2
=
βλ  2π 
βλ
π ⋅g
sin
s
=
sin
2π ⋅ g  βλ  − g / 2 π ⋅ g
βλ
Der Energiegewinn durch einen Resonator bei einem Umlauf ist
∆E sHF = q ⋅ g ⋅ E0T sin ϕ s = q ⋅U eff sin ϕ s = q ⋅ RB& ⋅ C s
Beispiel SIS18: R = 10 m, Cs = 216,72 m,
U eff sin ϕ s = RB& ⋅ C s
B& = 10 T/s
⇒ U eff sin ϕ s = 22 kV
SS2014
8.18