Berechnungen in der Astronomie - Schulen

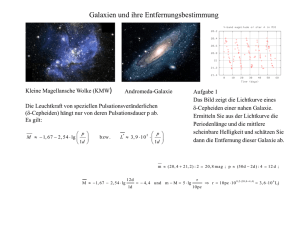
Inhaltsverzeichnis
1.: Die Bestimmung des Erdumfanges
1
2.: Die Entfernung des Mondes
1
2.1: Die Entfernungsberechnung durch Aristarch
1
2.2: Die Entfernungsberechnung durch Hipparchos
1
2.3: Die Entfernungsberechnung durch Lalande und Lacaille
2
3.: Die Keplerschen Gesetze
3
3.1: Die Planetengesetze
3
3.2: Die Keplersche Gleichung
3
4.: Das Newtonsche Gravitationsgesetz
3
5.: Die Bestimmung der Lichtgeschwindigkeit
4
6.: Die Entfernung offener Sternhaufen
5
7.: Delta-Cepheiden als Meilensteine
6
8.: Das Hubblesche Expansionsgesetz
7
9.: Die spezielle und allgemeine Relativitätstheorie
8
9.1: Die spezielle Relativitätstheorie
8
9.1.1: Zeitdilatation
8
9.1.2: Äquivalenzbeziehung
8
9.2: Die allgemeine Relativitätstheorie
9
9.2.1: Schwarze Löcher
9
1.: Die Bestimmung des Erdumfanges
Zur Zeit der Sommersonnenwende stand in
mittelpunkt einen Winkel von 7,2° bilde-
der Antike im damaligen Syene, dem heu-
ten, schloss Eratosthenes auf einen Erdum-
tigen Assuan, die Sonne zu Mittag exakt
fang von 252000 Stadien (40320 km).
im Zenit, da man ihr Spiegelbild in einem
Damit war schon im 3. Jhdt v. Chr. der
tiefen Brunnen sehen konnte. Hingegen
Erdumfang erstaunlich genau bekannt.1 2
sah man in Alexandria zur selben Zeit den
1
Schatten eines Obelisken unter einem mittäglichen Zenitwinkel der Sonne von 1/50
des Vollkreises (7,2°). Da die beiden Orte
ca. 5040 Stadien (1 Stadion160m) vonei-
Vgl. PCE-NET GMBH: Erdradius nach
Eratosthenes und Posidonius. Online im Internet:
URL: http://www.erft.de /schulen/abteigym/physik/radius.htm [Stand: 2002-11-11]
2
Vgl. SCHAMAGL, Reinhard: Die Mogelei des
Erathostenes. Online im Internet: URL:
http://www.rescon.de /Wissen/AstroErat2.html
[Stand: 2002-11-11]
nander entfernt waren und mit dem Erd-
2.: Die Entfernung des Mondes
2.1: Die Entfernungsberechnung durch Aristarch von Samos (310 bis 230 v. Chr.)
Aristarch berechnete das Verhältnis der
Aristarch fand für  den Wert 87°. Dem-
Mondentfernung zur Sonnenentfernung,
entsprechend fand er für das Entfernungs-
indem er den Winkel  maß, den die bei-
verhältnis Mond : Sonne = cos(87°) einen
den Himmelskörper zum Zeitpunkt des
Wert von 0,052…. Das ergab, dass die
Halbmondes bilden. In dieser Konstellation
Sonne 19 mal weiter entfernt ist als der
bilden Sonne und Mond mit der Erde ein
Mond. (In Wirklichkeit ist der Winkel  =
rechtwinkeliges Dreieck, wobei der rechte
89°51’, was ein Verhältnis von 1 : 382
Winkel im Mond liegt.
ergibt.)
2.2: Die Entfernungsberechnung durch Hipparchos von Nikaia (190 bis 120 v. Chr.)
Hipparchs Berechnung der Mondentfer-
2.) Der scheinbare Sonnenradius,
den
nung ist ein Meilenstein in der Astronomie.
Archimedes zu  = 15’ bestimmt hat.
Die wenigen Informationen, die ihm über
3.) Die Winkelgeschwindigkeit, mit der
Sonne und Mond zur Verfügung standen,
sich der Mond relativ zu den Fixster-
waren folgende:
nen bewegt (30,5’ pro h).
1.) Das Entfernungsverhältnis Mond :
4.) Die Zeit, die der Mondmittelpunkt bei
Sonne, das Aristarch von Samos schon
einer
ca. hundert Jahre zuvor zu 1:19 be-
Durchlaufen des Erdschattens benötigt
stimmt hatte.
(2h 40min = 8/3 h).
totalen
Mondfinsternis
zum
Im Zentrum seiner Überlegung steht fol-
Erdschattens in der Entfernung des Mon-
gende Frage: Unter welchem Winkel sieht
des. Für  berechnet man unmittelbar:  =
man vom Mond aus
30,5’*
8/3*1/2
=
den Erdradius?
(81,333...’)/2. Zwischen
Ansatz: , .....Winkel, unter denen der
den vier Winkeln besteht folgende Bezie-
Erdradius auf der Sonne bzw. dem Mond
hung:  +  =  + 
erscheint (In der eingescannten Grafik3
Da  und  sehr kleine Winkel sind, gilt in
wird  durch ein  mit einer Sonne und 
guter Näherung:
durch ein  mit einem Mond ersetzt.). .....
*(1 + 1/19) = 15’ + (81,333...’)/2.
Scheinbarer
Bildet man von diesem Wert für  den
halber
Durchmesser
des
3
DIE FASZINIERENDE WELT DER ASTRONOMIE, Infoware Multimedia Ltd., KOCH Media
Ges.m.b.H. Austria, 1999
 :  = 1 : 19
Tangens, so erhält man, dass der Mond 65
Erdradien entfernt ist.
2.3: Die Entfernungsberechnung durch Lalande und Lacaille
Mit Hilfe genauerer Messinstrumente war
Winkeln: 1 + 2 = 1 + 2 - 1 - 2.
es im neunzehnten Jahrhundert möglich,
Die Anwendung des Sinussatzes ergibt:
die Entfernung des Mondes durch Triangu-
sin(1) / sin(180 - 1) = r / e bzw.
lierung zu bestimmen. Dazu peilt man von
sin(2) / sin(180 - 2) = r / e.
zwei möglichst weit entfernten Punkten der
Wegen der Kleinheit der Winkel 1 und 2
Erdkugel (z.B. Wien mit der nördlichen
darf man vereinfachen zu:
geografischen Breite 1 = 48°15’ und
1 = (r / e)*sin(1) und 2 = (r / e)*sin(2).
Kapstadt mit der südlichen Breite 2 =
Setzt man diese Terme in die Gleichung
33°58’), die etwa dieselbe geografische
zwischen den Winkeln ein, so erhält man:
Länge haben, einen markanten Punkt des
e = r*(sin(1)+sin(2)) / (1 + 2 - 1- 2).
Mondes an, wie zum Beispiel den hellen
Mit den obigen Daten ergibt das für die
Krater des Mondes, genannt Kepler. Dabei
Entfernung des Mondes von der Erde einen
hat man folgende Zenitdistanzen gemes-
Wert von etwas mehr als 60 Erdradien.4 5
sen: Wien 1 = 27°41’ und Kapstadt 2 =
55°45’.
Ansatz: 1, 2.....Winkel, unter dem die
Strecke Erdmittelpunkt – Wien (bzw.
Kapstadt) am Messpunkt auf dem Mond
erscheint. r.....Erdradius, e.....Entfernung
des Mondes. Beziehung zwischen den
Vgl. RUPRECHT GYMNASIUM  LEIFI: Bestimmung der Mondentfernung durch Triangulierung. Online im Internet: URL:
http://www.physik.uni-muenchen.de
/didaktik/U_materialien/leifiphysik/web_ph11/umw
elt-technik/10entfernungen/mondentfernung.htm
[Stand: 2002-11-12]
5
Vgl. HERRMANN, Dieter B.: Kosmische Weiten.
Geschichte der Entfernungsmessung im Weltall. 2.
Aufl. Leipzig: Johann Ambrosius Barth, 1981.
4
3.: Die Keplerschen Gesetze
3.1: Die Planetengesetze
b2 = r*(2a – r)*sin2()
Tycho Brahe war kaiserlicher Astronom
am Hofe Rudolfs II. in Prag. Er machte
2. Der von der Sonne zu einem Planeten
ohne Fernrohr genaue Aufzeichnungen
gezogene Radiusvektor überstreicht in
über den Lauf der Planeten. Sein Nachfol-
gleichen
ger Johannes Kepler stellte beim Studium
r*v*sin()/2 = a*b*/T
Zeiten
gleiche
Flächen.
dieser Tabellen Unregelmäßigkeiten bei
3. Die Kuben der großen Bahnachsen
den Zahlenwerten der Marsbahn fest. Die
verhalten sich wie die Quadrate der
Lösung dieses Problems führte ihn zur
Umlaufszeiten.
Aufstellung der nach ihm benannten Ge-
a3 : T2 = C
setze.
(C ist im Sonnensystem konstant und
1. Die Planeten bewegen sich auf Ellipsen
kann aus den Daten der Erdbahn
um die Sonne als Brennpunkt.
berechnet werden.)
3.2: Die Keplersche Gleichung
Schwieriger als die Berechung der Bahn-
Gleichung transzendent, sodass E nur
elemente gestaltete sich für Kepler die Be-
durch eine Approximation berechnet wer-
stimmung der Position eines Planeten zu
den kann. Aus E kann schließlich mit der
einem bestimmten Zeitpunkt. Die Lösung
dieses Problems gelang ihm durch Einfüh-
Gleichung

1 
E
tan( ) 
tan( )
2
1 
2
der
rung einer Hilfsgröße, der exzentrischen
Polarwinkel  ermittelt werden. Das ist
Anomalie E. Diese kann aus der numeri-
jener Winkel, den die Strecke Sonne – Pla-
schen Exzentrizität und der Umlaufszeit
net mit der Bahnachse bildet.6
für jeden Zeitpunkt aus der Keplerschen
Gleichung
E   * sin( E ) 
berechnet
werden:
2 * t
. Leider ist diese
T
6
Vgl. UNSÖLD, Albrecht / BASCHEK, Bodo: Der
neue Kosmos. 5., überarb., erw. Aufl. Berlin, Heidelberg u.a.: Springer Verlag, 1991.
4.: Das Newtonsche Gravitationsgesetz
Isaac Newton hat sein Gravitationsgesetz
aus den Keplerschen Gesetzen abgeleitet:
K G
m1 * m2
. G bedeutet die unir2
verselle Gravitationskonstante, deren Wert
6,67259*10-11m3kg-1s-2 beträgt. Die Leis-
man für die Halbachse a 42239km. Zieht
tung Newtons besteht darin, dass er durch
man den Erdradius ab, so ergibt das eine
das Gravitationsgesetz die gesamte Him-
Höhe von knapp 36000km.
melsmechanik auf ein einziges Grundprin-
Die Masse eines Himmelskörpers – etwa
zip
die
der Sonne – kann leicht berechnet werden,
Keplerschen Gesetze in ihrer ursprüngli-
wenn man die mittlere Entfernung a und
chen Form nur für das Sonnensystem gal-
die Umlaufszeit T eines (massearmen) Sa-
ten, können sie nun auf eine allgemein
telliten kennt. Setzt man die Umlaufszeit
gültige Form gebracht werden. Es muss
der Erde und ihre Entfernung von der Son-
nur das 3.Keplersche Gesetz umgeformt
ne ein, diesmal bleibt die Erdmasse unbe-
werden zu:
rücksichtigt, erhält man für die Masse der
a 3 G * (m1  m2 )

.
T2
4 2
Sonne unmittelbar 2*1030 kg.7 8
zurückgeführt
hat.
Während
7
Die Bedeutung dieser Formel soll nun an
zwei
Beispielen
demonstriert
werden:
Standortsatteliten für Television und Meteorologie umkreisen die Erden in genau
24h, sodass sie von der Erde aus gesehen
Vgl. GROSSMANN, Alexander, Dr.: Physikalische Konstanten für Naturwissenschaft und Technik [Datenstand 2000]. Berlin: Wiley-VCH Verlag,
2001.
8
Vgl. SCHAIFERS, Karl / TRAVING, Gerhard:
Meyers Handbuch über das Weltall. 5. bearb., wesentl. erw. Aufl. Wien u.a.: Meyers Lexikonverlag,
1973.
scheinbar immer an der gleichen Stelle des
Himmels stehen. Setzt man für die Erdmasse 5,977*1024 kg ein (Die Satellitenmasse
wird
vernachlässigt),
erhält
5.: Die Bestimmung der Lichtgeschwindigkeit
Die Philosophen der Antike und auch noch
Erfolg. Daher gelang die Messung erst
der Physiker Newton glaubten, dass sich
durch Benutzung der ungeheuren Distan-
das Licht mit unendlicher Geschwindigkeit
zen zwischen den Himmelskörpern im
ausbreite. Zwar hatte Galilei schon um
Sonnensystem.
1604 die Vermutung
Olaf Römer war 1676
gehabt,
die
der erste, der die Licht-
Lichtgeschwindigkeit
geschwindigkeit c aus
endlich sei und er
astronomischen
versuchte sie auch zu
obachtungen,
messen,
den Verfinsterungen der
dass
aber
ohne
Benämlich
Jupitermonde, berechnet hat. Eine Verfins-
nete 144. Verfinsterung mit einer Ver-
terung ereignet sich immer dann, wenn ein
spätung von 17min (1000sec) eintritt.
Mond in den Schatten des Jupiter eintritt.
Römer fand die richtige Erklärung.
Diese Ereignisse finden in gleichen zeitli-
Der Weg, den das Licht vom Jupitermond
9
chen Abständen statt. Bei Io(Bild) , dem
bis zur Erde zurücklegt, ist ein halbes Jahr
innersten Jupitermond, beträgt diese Zeit
später um den Durchmesser der Erdbahn
1d 6h 21min 16sec. Dementsprechend ver-
länger. Für diese zusätzliche Strecke
schwindet er in Laufe eines Jahres 288-mal
braucht das Licht also 1000 Sekunden län-
im Schatten des Planeten. Zählt man nun
ger. Das ergibt für die Lichtgeschwindig-
seine Verfinsterungen, beginnend im Zeit-
keit den Wert c = 2*150*106 km /
punkt geringster Jupiterentfernung zur Er-
1000sec.Das sind exakt 300000km/sec.10
de (Opposition) bis zum Zeitpunkt der
größten Jupiterentfernung (Konjunktion),
so stellt man fest, dass die vorausberech-
Ges.m.b.H. Austria, 1999
10
Vgl. BORN, Max (Hrsg.): Die Relativitätstheorie
Einsteins. 4.Aufl. Berlin, Göttingen, Heidelberg:
Springer-Verlag, 1964.
9
DIE FASZINIERENDE WELT DER ASTRONOMIE, Infoware Multimedia Ltd., KOCH Media
6.: Die Entfernung offener Sternhaufen
So wie man in der Physik den Kraftauf-
obachtungspunkt B aus beobachten wir bei
wand in eine Richtung in eine horizontale
dieser Sterngruppe den Fluchtpunkt des
und eine vertikale Kraft zerlegen kann, so
Sternhaufens. Wir kennen also die Flug-
funktioniert dieses Prinzip auch bei der
richtung und daher die Richtung der Ge-
Entfernung
offener
schwindigkeit
des
Sternhaufen. Man zer-
Sterns S. Der Dopp-
legt hierbei die Ge-
ler-Effekt
gibt
schwindigkeit
seine
Radialge-
in
die
Radialgeschwindigkeit
uns
schwindigkeit an. Das
und in die Geschwindigkeit quer zur Blick-
in (a) grau gezeichnete Dreieck ist damit
richtung. Bei der abgebildeten Grafik11
eindeutig bestimmt, denn wir kennen die
geht es dreimal um rechtwinklige Drei-
Radialgeschwindigkeit und den Winkel bei
ecke, bei denen aus zwei Teilstücken ein
S, der gleich dem Winkel zwischen Vertex
drittes bestimmt wird. Von unserem Be-
und S ist. Daraus folgt die wahre Geschwindigkeit. In (b) wird dasselbe Drei-
11
KIPPENHAHN, Rudolf: Licht vom Rande der
Welt. Das Universum und sein Anfang. Durchgesehene Neuaufl.(1987) München u.a.: Piper 1984. S.
eck, von dem wir jetzt alles wissen, be-
messen wir etwa in Parsec pro Jahrhundert,
nützt, um die Geschwindigkeit quer zur
die Eigenbewegung in Bogensekunden pro
Blickrichtung zu bestimmen, die wir in (c)
Jahrhundert. Damit ist das graue Dreieck in
benützen. Diese Geschwindigkeit ist in (c)
(c) eindeutig bestimmt. Die Entfernung des
von S ausgehend eingezeichnet. Nehmen
offenen Sternhaufens berechnet man jetzt
wir jetzt noch die durch direkte Beobach-
einfach mit der Tangensfunktion:
tung bestimmte Eigenbewegung dazu. Die
Entfernung e = tan (Eigenbewegung) / Ge-
Geschwindigkeit quer zur Blickrichtung
schwindigkeit quer zur Blickrichtung.12
337.
12
Vgl. KIPPENHAHN, Rudolf: A. a. O., S.337.
7.: Delta-Cepheiden als Meilensteine
Bei den Delta-Cepheiden handelt es sich
ligkeit ihre Entfernung berechnen kann.
um pulsationsveränderliche Sterne, die
Noch bis ins 20. Jhdt. glaubte man, dass
periodisch in Zeiträumen von ein bis hun-
der Andromedanebel, der eigentlich eine
dert Tagen ihre Helligkeit verändern. Die
eigene Galaxie ist, ein Nebel innerhalb
Sterne blähen sich auf und fallen wieder
unserer Galaxis sei. Edwin Hubble ent-
zusammen. Als erste erkannte Henrietta
deckte am seinerzeit größten Teleskop der
Leavit, dass die absolute Helligkeit und die
Erde auf dem Mt.Wilson einige Delta-
Periodendauer
von
Cepheiden, aus deren
sich
proportional
verhalten. Sie hat
insbesondere DeltaCepheiden
Großen
in
der
Helligkeit
Delta-Cepheiden
14,0
12,0
10,0
8,0
6,0
4,0
2,0
0,0
Periode und scheinbarer Helligkeit er die
Entfernung der Sterne,
und damit auch die
0
10
Magellan-
20
Zeit in Tagen
30
Entfernung
Andromedanebels,
des
zu
schen Wolke untersucht und mit der
einer Million Lichtjahre bestimmte. Hub-
Leuchtkraft - Perioden-Beziehung ein Re-
ble lag zwar mit einer Million Lichtjahre
ferenzsystem für die Entfernung von Ga-
weit unter dem heutigen Wert von 2,2 Mil-
laxien und Nebeln mit Delta-Cepheiden
lionen Lichtjahren, konnte aber nachwei-
geschaffen. Somit wurden die Cepheiden
sen, dass der Andromedanebel kein Nebel
zu Meilensteinen im Universum, da man
in unserer Galaxis, sondern eine eigene
aus der Länge ihrer Periodendauer die ab-
Galaxie ist. Es wurde nicht nur die Entfer-
solute Helligkeit, und aus der Differenz
nung des Andromedanebels mit Hilfe von
zwischen scheinbarer und absoluter Hel-
Delta-Cepheiden berechnet, sondern auch
die Entfernung weit entfernter Galaxien,
ta-Cepheiden zu finden und ihre Periode zu
bei denen die Delta-Cepheiden durch lang-
bestimmen.13
belichtete Photoplatten erfasst wurden.
13
Doch umso weiter eine Galaxie von uns
Vgl. STUMPFF, Karl (Hrsg.): Astronomie.
Hamburg u.a.: Fischer Bücherei, 1957.
entfernt ist, desto schwieriger wird es Del-
8.: Das Hubblesche Expansionsgesetz
Wie schon erwähnt, arbeitete Edwin Hub-
dass sich fast alle Galaxien von uns fort-
ble am seinerzeit größten Teleskop der
bewegen. Die Rotverschiebung z = ( -
Erde am Mt. Wilson. Er beschäftigte sich
0)/0 war dabei um so größer, je weiter
in erster Linie mit Galaxien. Er untersuchte
entfernt man die Galaxie vermutete - wo-
die Formen der Galaxien und klassierte sie
bei  die astronomisch gemessene Wellen-
in elliptische, Spiral- und balkenförmige
länge und 0 die im Labor gemessene Wel-
Galaxien. Er untersuchte auch die Spektren
lenlänge ist. Dies war der Zeitpunkt, als
der Galaxien und entdeckte die chemischen
das Modell für das expandierende Univer-
Elemente, die auch in unserer Galaxie ge-
sum geschaffen wurde. Zwar hätte schon
funden wurden. Allerdings fiel ihm auf,
Albert Einstein die Expansion des Univer-
dass die Spektrallinien, die durch die Ele-
sums durch die allgemeine Relativitätsthe-
mente der Materie der fernen Galaxien
orie vorhersagen können, doch selbst Al-
erzeugt werden, leicht verschoben sind.
bert Einstein war Zeit seines Lebens fest
Die bekannten Spektrallinien waren in den
von einem stationärem Universum über-
meisten Galaxien etwas in den roten Be-
zeugt. Um nun die Entfernung einer Ga-
reich verschoben. Es gab allerdings auch
laxie zu bestimmen, muss man die gemes-
Galaxien mit einer Verschiebung der
sene Rotverschiebung kennen und als
Spektrallinien in den blauen Bereich des
zweiter Faktor muss die Größe oder die
Spektrums, wie etwa die Andromeda-
Geschwindigkeit der Expansion bekannt
galaxie. Hubble selbst hatte schon die rich-
sein. Diesen Faktor nennt man Hubble-
tige Idee. Die Rotverschiebung wird durch
Konstante. Sie gibt an, mit wie viel Kilo-
den Dopplereffekt verursacht; bewegt sich
metern pro Sekunde sich das Universum
eine Galaxie von uns weg, so kommt ihr
pro Megaparsec (Mpc) ausdehnt. Heute
Licht bei uns mit vergrößerter Wellenlänge
schätzt man die Hubble-Konstante auf et-
an – und umgekehrt. Wie Hubble erkannte,
wa 60-75 km/s pro Mpc. Die Hubble Kon-
findet man bei den meisten Galaxien eine
stante ist deshalb so schwer bestimmbar,
Rotverschiebung. Dies würde bedeuten,
weil sich schon ein kleiner Messfehler
stark auswirkt. Wichtig ist die Hubble-
Hubble-Konstante kommt man auf ein
Konstante auch für die Bestimmung des
Weltalter von ca. 15 Mrd. Jahren.14
Weltalters. Um so kleiner ihr Wert ist, des14
to langsamer verläuft die Expansion und
desto älter ist das Universum. Mit der
heutzutage
gebräuchlichen
Größe
Vgl. UNSÖLD, Albrecht / BASCHEK, Bodo:
Der neue Kosmos. 5., überarb., erw. Aufl. Berlin,
Heidelberg u.a.: Springer Verlag, 1991.
der
9.: Die Relativitätstheorie
9.1: Die spezielle Relativitätstheorie
Albert Einstein ist bei der Ausarbeitung
gleichwertig.
dieser fundamentalen Theorie im Jahre
Die Newtonsche Mechanik stellt einen
1905 von zwei experimentell abgesicherten
Spezialfall
Grundannahmen ausgegangen:
theorie dar. Man erhält die alten, klassi-
1. Die Lichtgeschwindigkeit kann nicht
schen Gesetze, wenn man in den neuen
überschritten werden.
der speziellen Relativitäts-
Formeln für die Lichtgeschwindigkeit den
2. Alle Inertialsysteme sind physikalisch
Wert unendlich annimmt.
9.1.1: Zeitdilatation
Die Relativitätstheorie enthält mehrere
len mit einer Halbwertszeit von 2,15*10-6
merkwürdige Aussagen. Zum Beispiel
sec und bewegen sich mit 99,98% der
folgt aus ihr, dass bewegte Uhren gemäß
Lichtgeschwindigkeit. Ohne Berücksichti-
der Beziehung t  t R 1  v 2 / c 2 langsamer
gung der Zeitdilatation könnten die -
gehen. Darin ist v die Geschwindigkeit der
Mesonen nur einen Weg von 3*108*2*106
bewegten Uhr, t und tR sind die Zeitanga-
m = 600m zurücklegen. Die korrekte
ben der bewegten bzw. der ruhenden Uhr.
Rechnung ergibt jedoch für den Wurzel-
Ein interessanter Effekt ist die Existenz der
ausdruck
-Mesonen in der kosmischen Strahlung,
geht für diese Teilchen die Zeit 50mal
die auf der Erdoberfläche registriert wird.
langsamer und sie legen bis zu ihrem Zer-
Diese Teilchen entstehen infolge hoch-
fall 50*600m = 30km zurück. Sie können
energetischer Strahlung aus dem Weltall in
also nur auf Grund dieses relativistischen
der Stratosphäre in 30 km Höhe. Sie zerfal-
Effekts auf der Erde beobachtet werden.
9.1.2: Äquivalenzbeziehung
1  0.9998 2  0,02 . Daher ver-
Die bekannteste Formel der Relativitäts-
luss
von
der
Sonne
beträgt
daher
theorie ist wohl E = m*c2. Eine einfache
4*(1,5*1011m)2*1,4*103W/m2
Rechnung ergibt, dass 1kg Materie einer
3.8*1026W. Dividiert man diesen Wert
Energie von 9*1016 Joule entspricht. Das
durch das Massenäquivalent für 1kg, so
bedeutet, dass Sterne infolge ihrer Strah-
erhält man als überraschendes Ergebnis,
lung Masse verlieren. Die Strahlungsleis-
dass die Sonne in jeder Sekunde 4000000t
tung der Sonne wird durch die Solarkon-
Masse verliert! Wenn man das Alter der
stante angegeben. Man misst, dass auf ei-
Sonne mit 15 Milliarden Jahren stark über-
nen m2 in der Entfernung der Erde bei
schätzt, dann hat die Masse der Sonne in
senkrechtem Lichteinfall 1400 Watt Son-
dieser Zeit durch Abstrahlung trotzdem nur
nenenergie fallen. Der gesamte Energief-
um weniger als 0,1% abgenommen.
oder
9.2: Die allgemeine Relativitätstheorie
In
der
allgemeinen
Relativitätstheorie
stand des Beobachters wesentlich bestimmt
(ART), die Einstein im Jahr 1915 aufge-
werden. Diese Theorie gehört zu den
stellt hat, erklärte er die Gravitationskraft
schwierigsten in der gesamten Physik, weil
durch eine Krümmung der Raum-Zeit.
ihr mathematischer Aufbau die Riemann-
Während Isaac Newton noch von der Exis-
sche Geometrie verwendet und ihre voll-
tenz einer überall gleich laufenden Zeit
ständige Darstellung nur mittels der Ten-
und einem absoluten Raum überzeugt war
sorrechnung möglich ist. Trotzdem können
und der große Philosoph Immanuel Kant
ihre wesentlichen Aussagen auch mit „ge-
diese sogar als denknotwendige Kategorien
wöhnlicher Mathematik“ verstanden wer-
ansah, fasste sie Einstein zu einer Einheit
den.
zusammen, deren Eigenschaften vom Zu-
9.2.1: Schwarze Löcher
Zur sicherlich merkwürdigsten Konse-
Größe nennt man seinen Schwarzschildra-
quenz der ART gehört die Existenz
dius. Seine Berechnung ist einfach, da man
„Schwarze Löcher“.
lediglich die kinetische und die potentielle
Wird eine Masse auf eine bestimmte Größe
Energie eines Photons gleichsetzen muss.
komprimiert, so wird die Gravitationskraft
Physikalisch bedeutet das, dass die Bewe-
so groß, dass das Objekt in sich zusam-
gungsenergie des Lichtteilchens gerade
menstürzt und nichts kann aus ihm entwei-
nicht mehr zum Verlassen des Schwarzen
chen – auch kein Licht. Diese kritische
Lochs ausreicht:
1
M *m
. Daraus folgt für den
m *c2  G *
2
R
Schwarzschildradius: R 
2*G * M
.
c2
Für die Erde ergibt das:
R
2 * 6,67259 *10 11 * 5,977 *10 24
=
300000000 2
0.00886 m ≈ 1 cm.15 16
Cygnus X1 im Sternbild Schwan war das
erste Schwarze Loch, das von den Astronomen entdeckt wurde.
15
Vgl. GERTHSEN, Christian / KNESER, Hans
O.: Physik. Ein Lehrbuch zum Gebrauch neben
Vorlesungen. 9.Aufl. Berlin u.a.: Springer Verlag,
1966.
16
Vgl. TEAM C007571, Angie, Matthias and Thorsten: Black Holes aren’t black – After Hawking
they shine. Online im Internet: URL:
http://www.thinkquest.org/C007571/german/advanc
e/formulas.htm [13.08.2000]
Literaturverzeichnis:
Born, Max (Hrsg.): Die Relativitätstheorie Einsteins. 4. Aufl. Berlin, Göttingen,
Heidelberg: Springer Verlag, 1964
DIE FASZINIERENDE WELT DER ASTRONOMIE, Infoware Multimedia
Ltd., KOCH Media Ges.m.b.H. Austria, 1999
Gerthsen, Christian / Kneser, Hans O.: Physik. Ein Lehrbuch zum Gebrauch neben Vorlesungen. 9. Aufl. Berlin u.a.: Springer Verlag, 1966
Grossmann, Alexander, Dr.: Physikalische Konstanten für Naturwissenschaft
und Technik [Datenstand 2000]. Berlin: Wiley-VCH Verlag, 2001
Herrmann, Dieter B.: Kosmische Weiten. Geschichte der Entfernungsmessung
im Weltall. 2. Aufl. Leipzig: Johann Ambrosius Barth, 1981
Kippenhahn, Rudolf: Licht vom Rande der Welt. Das Universum und sein Anfang. Durchgesehene Neuaufl. (1987) München, Zürich: Piper, 1984
PCE-Net Gmbh: Erdradius nach Erathostenes und Posidonius. Online im Internet: URL: http://www.erft.de/schulen/abtei-gym/physik/radius.htm [11.11.02]
Ruprecht Gymnasium  LEIFI: Bestimmung der Mondentfernung durch Triangulierung. Online im Internet: URL: http://www.physik.unimuenchen.de/didaktik/U_materialien/leifiphysik/web_ph11/umwelttechnik/10entfernungen/mondentfernung.htm [11.11.02]
Schaifers, Karl / Traving, Gerhard: Meyers Handbuch über das Weltall. 5. bearb., wesentl. erw. Aufl. Wien u.a.: Meyers Lexikonverlag, 1973
Schamagl, Reinhard: Die Mogelei des Eratosthenes (Messprinzip). Online im
Internet: URL: http://www.rescon.de/Wissen/AstroErat2.html [11.11.02]
Stumpff, Karl (Hrsg.): Astronomie. Hamburg u.a.: Fischer Bücherei, 1957
Team c007571, Angie, Matthias and Thorsten: Black Holes aren’t black – After
Hawking they shine. Online im Internet: URL:
http://www.thinkquest.org/C007571/german/advance/formulas.htm [13.08.2000]
Unsöld, Albrecht / Baschek Bodo: Der neue Kosmos. 5., überarb., erw. Aufl.
Berlin, Heidelberg u.a.: Springer Verlag, 1991