Übungsblatt für die 2. Übung am 28.10. bzw. 04.11. Kontrollfragen

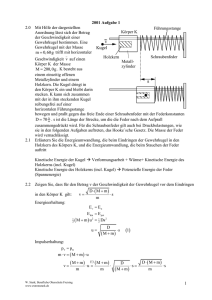
Übungsblatt für die 2. Übung am 28.10. bzw. 04.11.
Kontrollfragen:
1.) Was versteht man unter Kinematik?
2.) Nennen Sie Grundgrößen und abgeleitete Größen für die Kinematik?
3.) Warum ist der Drehwinkel kein (axialer) Vektor?
Rechenaufgaben:
Translation
1.) Wie groß ist die Beschleunigung eines aus der Ruhelage zum Zeitpunkt
t=0 startenden Körpers, der in der 6. Sekunde einen Weg von 6 Meter
zurücklegt?
2.) Die Bremse soll einen PKW, der die Geschwindigkeit v = 30 km/h hat,
innerhalb eines Weges von 10 Metern zum Stehen bringen. Berechnen
Sie a) die dazu erforderliche Zeit und
b) die Bremsbeschleunigung!
3.) Die Geschwindigkeit eines in einem Gefäß mit einer zähen Flüssigkeit
fallenden Körpers hängt in folgender Weise von der Zeit t ab:
v(t)=v0(1-e-qt) mit v0=4 cm/s und q=0,4/s
a) Wie groß ist die Geschwindigkeit zu den Zeitpunkten t = 0 s, t = 10 s
und für t gegen Unendlich?
b) Man bestimme allgemein die zeitlichen Abhängigkeiten s(t) und a(t)!
Man beachte dabei, dass zum Zeitpunkt t = 0 s bereits ein Weg s0= v0/q
zurückgelegt ist.
c) Stellen Sie a(t), v(t) und s(t) grafisch dar; diskutieren Sie die zeitlichen
Verläufe hinsichtlich der vorliegenden Bewegungsarten!
Drehbewegung – Rotation
4.) Eine Achse mit zwei kreisförmigen Papierscheiben, die voneinander den
Abstand l = 0,5 m haben, dreht sich mit einer Drehzahl von 1600/min.
Eine Gewehrkugel, die parallel zur Drehachse fliegt, durchschießt beide
Scheiben, wobei das Einschussloch der Kugel auf der zweiten Scheibe
gegenüber dem auf der ersten Scheibe um den Winkel 𝞅=12° verschoben
ist. Berechnen Sie die als konstant angenommene Geschwindigkeit der
Gewehrkugel! Welche Modellannahme ist hierzu nötig?
5.) Eine Schnecke kriecht mit der konstanten Geschwindigkeit v auf einem
kugelförmigen Luftballon entlang eines gedachten Meridians vom
Nordpol zum Südpol. Durch Aufblasen wächst der Radius des Ballons mit
konstanter Geschwindigkeit u. Kann die Schnecke den Südpol erreichen,
wenn ja, nach welcher Zeit? Begründen Sie Ihre Antwort!