Listen und Binäre Bäume

Binäre Bäume
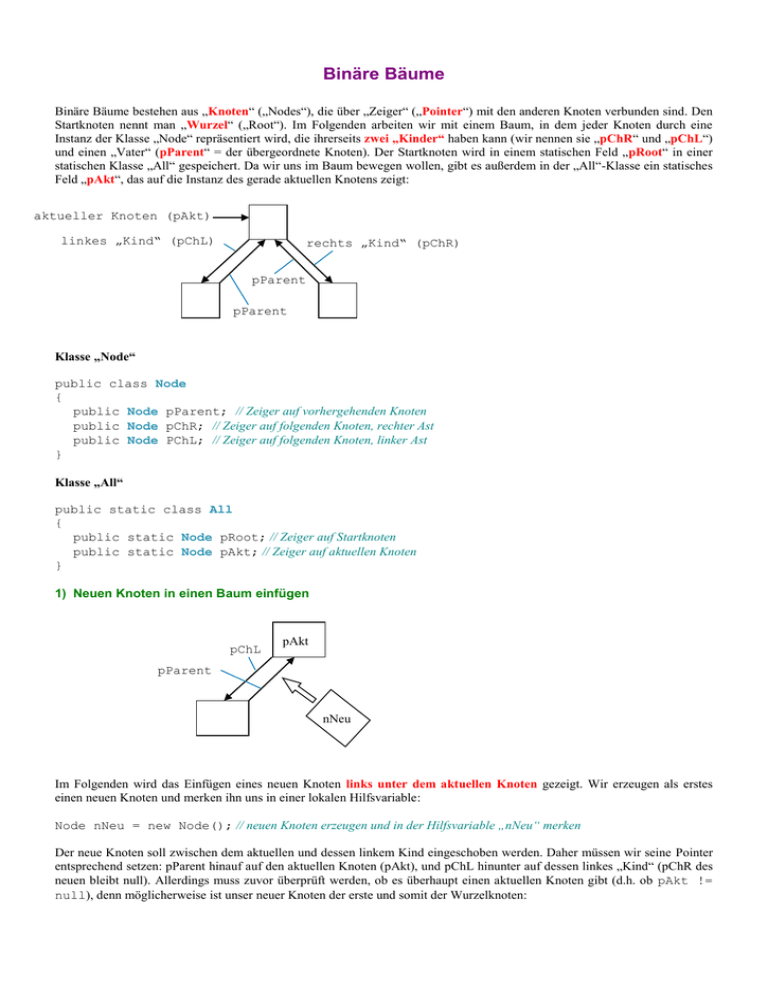
Binäre Bäume bestehen aus „Knoten“ („Nodes“), die über „Zeiger“ („Pointer“) mit den anderen Knoten verbunden sind. Den
Startknoten nennt man „Wurzel“ („Root“). Im Folgenden arbeiten wir mit einem Baum, in dem jeder Knoten durch eine
Instanz der Klasse „Node“ repräsentiert wird, die ihrerseits zwei „Kinder“ haben kann (wir nennen sie „pChR“ und „pChL“)
und einen „Vater“ (pParent“ = der übergeordnete Knoten). Der Startknoten wird in einem statischen Feld „pRoot“ in einer
statischen Klasse „All“ gespeichert. Da wir uns im Baum bewegen wollen, gibt es außerdem in der „All“-Klasse ein statisches
Feld „pAkt“, das auf die Instanz des gerade aktuellen Knotens zeigt:
aktueller Knoten (pAkt)
linkes „Kind“ (pChL)
rechts „Kind“ (pChR)
pParent
pParent
Klasse „Node“
public class Node
{
public Node pParent; // Zeiger auf vorhergehenden Knoten
public Node pChR; // Zeiger auf folgenden Knoten, rechter Ast
public Node PChL; // Zeiger auf folgenden Knoten, linker Ast
}
Klasse „All“
public static class All
{
public static Node pRoot; // Zeiger auf Startknoten
public static Node pAkt; // Zeiger auf aktuellen Knoten
}
1) Neuen Knoten in einen Baum einfügen
pChL
pAkt
pParent
nNeu
Im Folgenden wird das Einfügen eines neuen Knoten links unter dem aktuellen Knoten gezeigt. Wir erzeugen als erstes
einen neuen Knoten und merken ihn uns in einer lokalen Hilfsvariable:
Node nNeu = new Node(); // neuen Knoten erzeugen und in der Hilfsvariable „nNeu“ merken
Der neue Knoten soll zwischen dem aktuellen und dessen linkem Kind eingeschoben werden. Daher müssen wir seine Pointer
entsprechend setzen: pParent hinauf auf den aktuellen Knoten (pAkt), und pChL hinunter auf dessen linkes „Kind“ (pChR des
neuen bleibt null). Allerdings muss zuvor überprüft werden, ob es überhaupt einen aktuellen Knoten gibt (d.h. ob pAkt !=
null), denn möglicherweise ist unser neuer Knoten der erste und somit der Wurzelknoten:
if (All.pAkt != null) // gibt´s überhaupt einen aktuellen Knoten?
{
nNeu.PChL = pAkt.pChL; // das linke Kind des aktuellen wird zum linken Kind des neuen
nNeu.pParent = All.pAkt; // der aktuelle wird zum Parent des neuen
}
else
{
All.pRoot = pNeu; // falls es noch gar keinen Knoten gibt, wird unser neuer der Wurzelknoten des Baums
}
pChL
pAkt
pParent des neuen Knotens auf den aktuellen
Knoten hinaufzeigen lassen
pParent
nNeu
pChR des neuen Knotens
bleibt null
pChL des neuen Knotens auf den pChL des
aktuellen Knoten hinunterzeigen lassen
Die Pointer des neuen Knoten zeigen jetzt auf die richtigen Nachbarn (oben und unten), aber diese noch nicht auf ihn. Um ihn
in den Baum einzuhängen, müssen wir zwei Zeiger seiner Nachbar auf ihn „verbiegen“:
a) den pChL des aktuellen (hinunter auf den neuen)
b) den pParent vom Kind des aktuellen (hinauf auf den neuen)
Dabei ist zu überprüfen, ob der aktuelle Knoten überhaupt ein Kind besitzt, denn von einem nicht existierenden können wir
natürlich keinen Zeiger bearbeiten:
if (pChL != null)
{
pChL.pParent = nNeu;
}
All.pAkt.PChL = nNeu;
pChL
pAkt
pChL des aktuellen Knotens
auf den neuen hinunterzeigen
lassen
pParent
nNeu
null
Fertig:
pAkt
pChL
pParent des Kindes des aktuellen Knotens
auf den neuen hinaufzeigen lassen
pParent
pNeu
pChL
pParent
null
Zuletzt den neuen Knoten zum aktuellen machen:
All.pAkt = nNeu; // der neue Knoten ist ab jetzt der aktuelle Knoten
2) Element aus einem Baum entfernen
Wenn die Nachbarn des aktuellen Knotens ihre Zeiger von ihm „wegbiegen“, hängt er in der Luft und hat keine Verbindung
mehr zum Baum. Allerdings ist auf die Neuzuordnung dieser Zeiger zu achten:
if (All.pAkt != null) // gibt´s überhaupt einen aktuellen Knoten?
{
if (All.pAkt.pParent != null) // hat der aktuelle Knoten einen Parent?
{
Node nP = All.pAkt.pParent; // Hilfsvariable für den übersichtlicheren Zugriff auf den Parent
if (All.pAkt == nP.pChR) nP.pChR = null; // ist der aktuelle Knoten das rechte Kind seines Parents?
- dann dessen pChR auf null setzen
else nP.PChL = null; // andernfalls dessen pChL auf null setzen
All.pAkt = nP; // der Parent des aktuellen wird zum neuen aktuellen Knoten
}
else
{
All.pRoot = null; // wenn der aktuelle keinen Parent hat, ist er der Wurzelknoten. Nach dessen Entfernen
gibt´s keinen mehr ...
All.pAkt = null; // ... und auch keinen aktuellen
}
}
3) Einen Baum traversieren
Um alle Knoten eines Baumes zu zeichnen, genügt keine einfache Schleife, denn nach jedem Knoten kann sich der Baum
verzweigen. Man benutzt daher „rekursive“ Methoden, um Bäume zu durchlaufen („traversieren“).
Rekursion bedeutet, dass eine Methode sich selbst aufruft.
Im Eventhandler der PictureBox rufen wir eine solche rekursive Methode auf, die 4 Parameter erwartet: das Graphics-Objekt,
den Wurzelknoten und die Koordinaten dieses Wurzelknotens (hier: oben Mitte der PictureBox).
private void pBox_Paint(object sender, PaintEventArgs e)
{
int x = pBox.Width / 2; // Mitte der PictureBox
int y = 8; // Abstand vom oberen Rand
if (All.pRoot != null)
{
knotenRekZeichnen(e.Graphics, All.pRoot, x, y); // rekursive Methode aufrufen
}
}
Die rekursive Methode überprüft als erstes, ob der übergeben Knoten gültig (!= null) ist und ruft sich anschließend
zweimal selbst auf: einmal für den rechten Ast (x-Koord wird erhöht), einmal für den linken Ast (x-Koord wird verringert).
Erst danach erfolgt der eigentliche Zeichnen-Befehl (hier: Aufruf einer entsprechenden Methode in der Klasse Node):
private void knotenRekZeichnen(Graphics g, Node n, int x, int y)
{
if (n != null)
{
knotenRekZeichnen(g, n.pChR, x + 32, y + 32); // rechten Ast durchlaufen
knotenRekZeichnen(g, n.PChL, x - 32, y + 32); // linken Ast durchlaufen
n.zeichnen(g, x, y); // Aufruf der eigentlichen Zeichnen-Methode in der Klasse Node
}
}
Gezeichnet wird in diesem Fall von unten nach oben, weil der Baum zuerst bis zum Ende eines Astes durchlaufen wird, bevor
die Zeichnen-Methode zum Zug kommt.
Wie funktioniert die Rekursion?
Jedes Programm bekommt bei seinem Start einen speziellen, kleinen Speicherbereich zugewiesen (den „Stack“ oder „Stapel“),
der von zwei Zeigern verwaltet wird: einer zeigt auf den Beginn des Stacks, ein zweiter (der „Stackpointer“ - SP) auf die
aktuelle Position im Stack. Bei jedem Sprung in eine Methode werden an der aktuellen Position des Stacks drei Informationen
abgelegt:
 die „Rücksprungadresse“ (d.h. die Stelle im Quellcode, von der in die Methode gesprungen wurde), damit das Programm
nach Beendigung der Methode wieder zurückfindet
 die Parameter, die der Methode mitgegeben werden
 die lokalen Variablen, falls vorhanden
Dieser Bereich auf dem Stack wird erst nach Beendigung der Methode (durch Verschieben des „Stackpointers“) ungültig.
Genau das machen wir uns zu Nutze, indem wir die Methode nicht sofort verlassen, sondern sie solange immer wieder mit
dem nächsten Zeiger (PChR bzw. PChL) aufrufen, bis wir am Ende eines „Astes“ des Baumes angelangt sind (d.h. bis PChR
bzw. PChR == null). Auf diese Weise bleiben die Pointer eines jeden Knoten erhalten (für jeden Knoten wurde ein neuer
Block auf dem Stack angelegt und noch nicht gelöscht, da wir die Methode ja noch nicht verlassen haben).