SymbolischeSuche

Spezialvorlesung
Suchalgorithmen
Thema:
Symbolische Suche
Stefan Edelkamp
Struktur des Buchs
Überblick





BDDs und BDD-basierte Suche
Symbolische Exploration
BDD-BFS, BDD-Dijkstra, BDDA*
Symbolische Musterdatenbanken
Musterauswahlproblem



Bin-Packing
Genetische Algorithmen
Hybrid-Ansatz (BDDs + Externe Suche)
a1 : (at package p c)
a2 : (in package p t)
Zustand : ¬ a1  a2
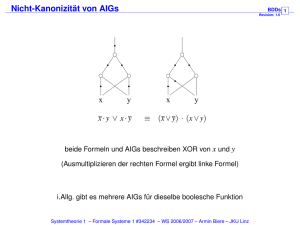
BDDs
a1
a1
a2
a2
a2
0
1
Binärer
Entscheidungsbaum
(RO)BDD
0
1
0
0
BDD-basierte Suche



Symbolische Repräsentation von
Zustandsmengen
Boole‘sche Formel States(a1,…,an)
Effiziente Zustandskodierung:

States(v1,…,vk), mit „finite domain“ variablen vi
Reduziert # möglicher, nicht # erreichbarer
Zustände

Variablenordnung wichtig, vgl.

Beispiel Kodierung Zustände
States(x) =
Zustandsmengen:
Symbolische Breitensuche

BFS: Si(x) repräsentiert alle Zustände die in i
Schritten erreichbar sind

Relationales Produkt:
Symbolische Exploration

Trans(x,x‘) beschreibt Transition Relation für
Image(x‘) = x States(x) Trans(x,x‘)
 Pre-Image(x) = x States(x‘)  Trans(x,x‘)
 Forwärts- and Rückwärtssuche sehr ähnlich

Pseudo-Code
Bidirektionale symbolische
Breitensuche
Schnitt
gefunden
s
g
Verfeinerungen:
Duplikatserkennung (BFS vs. BF-Tree Search):
 Terminierung
Partitionierte Berechnung:



1 Relation Trans-O für jeden Operator O
( and v commutieren)  Disjunktive Partition
Image(x‘) = VO (x States(x) Trans-O (x,x‘))
Symbolische Berechnung
kürzester Pfade

Vorraussetzungen:


Relation
Gewichtete
Transitionsrelation:
T(x,x‘,w) = 1, Übergang
von x nach x‘ hat
Kosten w  {0,1,…,C}
Pseudo-Code
Symbolischer Schätzer

Heuristische Relation:
H(w,x) = 1, Schätzwert
von x zum Ziel hat
Kosten w  {0,1,…,C}
Symbolisches A*

Idee:
Symbolische
Musterdatenbanken


Abstrakter Zustand (STRIPS): Original S  AP
„geschnitten“ mit Träger R  AP
Abstrakter Operator (P  R,A  R,D  R)
 Pfade bleiben erhalten!





Akkurate Zieldistanzen für jeden abstrakten Zustand
Untere Schranke für Zieldistanzen in Originalraum
BDD H[i] represäntiert Zustandsmenge { S | h(S) = i }
Konstruktion: Rückwärts-BFS
Symbolisch Musterdatenbanken: Wesentlich größere
DB können in geringerer Zeit berechnet werden
Speicher- und Zeitgewinn
(250 mio states/sec)
1600000
1400000
1200000
1000000
800000
600000
400000
200000
0
# States
# BDD Nodes
Approximierung der
Datenbankgröße
Addition von vi zum Träger korrespondiert zur
Multiplikation seines Wertebereichs zur
Abstraktionsraumgröße
v1
|v2|*|v3|
1. Füge Variable
gierig hinzu, bis
geschätzter
Speicherbedarf
überschritten
wird
2. Konstruiere
DB mit
ausgewähltem
|v1|*|v2|*|v3|
Träger
Musterauswahl durch
„BinPacking“
Abstract Zustandsraumgröße < Speichergrenze
Approximationen
z.B. „first fit“
Größen = |v1|*|v2|*|v4| |v6|*|v7|
*|v10|
|v3|*|v8|
|v5|*|v9|
Genetische
Musterdatenbanken
Problem:
 Auswahlstrategie beeinflusst
Effizienz
 Viele Muster
Vorschlag:
 GA mit Variablen Auswahl
Genen
 Initialisiert mit Bin Packing
 Spalte beschreibt Variable
 Zeile beschreibt Muster
Genetische Operatoren
Mutation (wichtigster Operator):
•Hinzufügen/Löschen von Variablen durch Bit-flippen
•Hinzufügen/Löschen von Mustern/Zeilen
Rekombination (selten genutzt):
•1-Bit „cross-over“
Auswahl:
•Abstracter Zustandsraum zu groß geringe Fitness
•Basiert auf mittleren Heuristisch Wert als Fitness
Während des Lernens werden PDBs konstruiert not benutzt!
Symbolisch Gerichtete Suche
Schätzer H: Relation von Paaren
H(value,state) = 1  h(state)=value
Beispiel: h(00 ) = h(01 ) = 1, h(10 ) = h(11 ) = 0
 H = {(value state ),(value ,¬state )}
Implementation: Alle Mengen-A*
Fachoperations auf BDDs
Optimalität und completeness: Von A*/IDA*
geerbt (konsistenter Schätzer)
2
0,
2
0
2
1
2
0
Greedy Best-First
BDDA*





BDD B(g,h,x) für Zustandsmenge mit f=g+h
BDD für Transitionsrelation T(x,x´)
- ein Ti für jeden Operator Oi, i = 1..k
Nachfolgermenge berechnet mit
Succ = Vi x Ti(x,x´) ^ B(g,h,x)
(partitionierte Berechnung)
BDD für H[i] (partitioniert, i = BFS Schicht)
BDD für min. Fach
B(g+1,h,x) = Succ ^ H[h]
Synergien

Mengen A*

BDD für Zustandsmenge
und (partitionierter)
Übergangsrelation
BDDA*

Duplikatserkennung mit
Boole’schen Operationen

Symbolische
Musterdatenbanken:
Schätzer mit Symbolic BFS
berechnet
BDDA*

h
Voraussetung:


0
Ungewichteter
Problemgraph
Konsistenter
Schätzer
1
2
3
4
BDD für
Zustände
5
6
0
1
g
 ∆h ={-1,0,1,2,…}
2
3
4
5
Schnitt der Nachfolger mit
H[0]H[1]H[2]H[3]H[4]H[5]H[6]
Pseudo-Code
B(0,h(I))  {I}
fmin  h(I)
while (fmin ≠ ∞)
g  min{i | B(i, fmin − i) ≠ }
h  fmin − g
B(g, h)  Reduziere(B(g, h))
Succ  GenerateNeighbors(B(g, h),T)
for each i = 1,...,max
B(g + 1, i)  B(g + 1, i) v (Succ ^ H[i])
fmin  min{i + j > fmin | Open(i, j) ≠ } U {∞}
Anzahl Iterationen
Quadratisch in optimaler
Lösungslänge
Symbolisches Branch-andBound (BFHS)
Gegeben untere Schranke U,
Berechnung entweder intern oder extern
Branching Partitioning

Wert eines Bits hängt nicht von den anderen ab

Heuristische Differenz in die Transitionsfunktion



▲1 T(x‘,x) = T(x‘,x)  ▲1 H(x,x‘)
▲0 T(x‘,x) = T(x‘,x)  ▲0 H(x,x‘)
▲-1 T(x‘,x) = T(x‘,x)  ▲-1 H(x,x‘)
Kostenoptimale symbolische
Suche

BDDs für lineare Ausdrücke (Bulzan, Barzis,
STTT 2005)

Metrik/Constraint: F(x) = a1*v1 + … an*vn




Berechne minF,maxF
Kodiere Wertebereich [0,maxF-minF]
Konstruiere BDD für F
Komplexität


Platz & Zeit: O(n *(a1+…+an))
… oft besser als mit ADDs
Gemischte symbolischexplizite Exploration
Viele disjunkte Musterdatenbanken als BDDs
(generiert in symbolischer Breitensuche)
 bilde Maximum über additive
Musterdatenbanken
 Externe und parallele explizite Suche
 Look-up: BDD-Repräsentation(state) 
BDD-Repräsentation(heuristik)
… H[i]

Beispiel: 35-Puzzle
1
3
2
18
20
4
5
6
7
25
24
8
15
10
11
21
28
12
13
14
9
27
28
22
30
34
35
17
16
29
31
33
34
26
32
Externalisierung





Packtierte Zustandscodierung: 32 Byte
(8 ints wobei 1 int = 5 Plättchen x 6 bits)
Datenbanken: 2x6er (je 5x6+1x5), 2x5er (je 7x5),
inkrementell generiert auf 16 GB,
7er gross, entspricht 36 x 35 x 34 x 33 x 32 x 31 x 30
Zuständen)
Symmetrischer Lookup: Transponierte Stellung wird
auch nachgeschaut
Inkrementelle Berechnung: Pro additiver Datenbank
zwei Einträge in den Zustandsvektor
Verteilte Berechnung




Annahme: Generierung schnell, Bewertung
langsam
Abwechselnd: Generierung (Master, kein
Datenbankzugriff) / Bewertung (Client)
Jeder Prozess ist für ein Plättchen zuständig
 35 + 1 Prozesse
Prozess muss laut Plättchen pro Menge
additiver DBen nur 1e ansprechen
 geringer Speicherplatz
Zusammenfassung
Ausblick: Suche mit
Automaten
Presburger Arithmetik (lineare Ausdrücke über den
natürlichen Zahlen) kann mit regulären Ausdrücken
beschrieben werden
 z.B. 4x + 5y ≤ 5
 Menge der akzeptierten Wörter im Automaten
entsprechen Zustandsmengen
 Idee: Tausche BDD durch EA, um unendliche
Zustandsräume zu traversieren
 Relationales Produkt: Konjunktion und Projektion
 Automatenminimierung nach jedem Schritt, um
Eindeutigkeit zu erhalten