Feststoffe:
Werbung

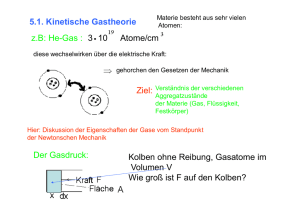
Aggregatzustände Inhaltsverzeichnis: Atomares Modell der Aggregatzustände Kräfte zwischen den Molekülen (Atomen) Feststoffe Flüssigkeiten Van der Waals – Kraft Elektrostatische Kraft zwischen Ionen H – Brückenbindungen Kovalente Bindungen (=Atombindungen) Unpolare Flüssigkeiten Polare Flüssigkeiten Beispiel Wasser Gase Ideales Gas Reales Gas Atomares Modell der Aggregatzustände: Zwischen zwei neutralen Atomen treten anziehende und abstoßende Kräfte auf, deren Überlagerung zu einer resultierenden Kraft F(r) und einer potentiellen Energie Ep(r) führt. Abhängig vom Abstand r zwischen den Kernen. Potentielle Energie Ep hängt von der Anordnung der wechselwirkenden Atome ab. F = - grad Ep Bei r0 besitzt Ep(r) ein Minimum; hier ist auch F(r) = 0! Bei kleineren Abständen → Abstoßung → Potential! Bei größeren Abständen → Anziehung → Potential! Kräfte zwischen den Molekühlen Van der Waals – Kraft Elektrostatische Kraft zwischen Ionen (400 – 700 kJ/mol) H – Brückenbindungen (0,5 - 5 kJ/mol ) (10-20kJ/mol ) Kovalente Bindungen (=Atombindungen) (100 – 400 kJ/mol) Van der Waals - Kraft: Zwischen unpolaren (ungeladenen) Molekühlen Die freien Elektronen in einem Molekül können sich frei bewegen, was zu einer ungleichmäßigen Ladungsverteilung im Molekül führt (temporärer Dipol). Grob, beziehungsweise in erster Näherung, kann ein Molekül mit Ladungsverschiebung als ein elektrischer Dipol (Zweipol) betrachtet werden. Dipole richten sich aus und gehen eine elektrostatische Wechselwirkung miteinander ein H – Brückenbindungen: Sie sind elektrostatischer Natur Moleküle treten über Wasserstoffatome (H) in Wechselwirkung Dazu muss das H kovalent an ein stark elektronegatives Atom (z. B. N, O, F und in manchen Fällen auch Cl) gebunden sein, was dem H eine positive Partialladung und dem Bindungspartner des H eine negative Partialladung verschafft, weil das elektronegativere Atom eine starke Anziehungskraft auf das gemeinsame Elektronenpaar ausübt. Man spricht von der Ausbildung eines positiven Pols (beim H) und eines negativen Pols (beim Bindungspartner des H), oft auch von einem starken Dipol. Die elektrostatischen Kräfte der Dipole führen zu einer Ausrichtung und gegenseitigen Anziehung der Dipole (der + Pol eines Dipols zieht den - Pol eines anderen Dipols an). Die Wasserstoffbrücke ist gebildet. Feststoffe: Kristalliner Festkörper: Atome in regelmäßigen Gitter angeordnet. Amorphe Festkörper: Atome mehr oder weniger statistisch verteilt. Bei einer absoluten Temperatur T schwingen die Atome um ihre Ruhelage mit Ekin= 12 kT Bei Temperaturen unterhalb des Schmelzpunktes ist die mittlere kinetische Energie klein gegen den Betrag der negativen potentiellen Energie Ep(r0). Federmodell eines Festkörpers: Flüssige Stoffe: Die kinetische Energie der Atome so groß, dass die Bindungsenergie nicht mehr ausreicht, um die Atome auf ihren Gitterplätzen festzuhalten. keine kristalline Ordnung, sondern Abstandsverteilung Rechts: Wahrscheinlichkeit W(r), dass ein Atom A0 einen Abstand r vom Nachbaratom hat: es ist noch eine gewisse Ordnung vorhanden! (Nahordnung) Energieminimum bei r0! Unpolare (einfache) Flüssigkeiten: quasi kugelförmige Teilchen z. B. Argon Ar, Stickstoff N2, Methan CH4 gegenseitige Abstoßung wegen Pauli-Prinzip für kleine Abstände gleichzeitig Anziehung durch Van der Waals Kräfte für große r Beschreibung durch Lennard-Jones-Potential: u(r ) 4 (( ) ( ) ) r r 12 6 Polare Flüssigkeiten: Moleküle ohne Symmetriezentrum (z.B. NH3,CO) tragen einen elektrischen Dipol μ Elektrostatische Kräfte wirken! In polaren Flüssigkeiten spielen kooperative Effekte eine Rolle: es entsteht ein neuartiges Verhalten. Bei der Berechnung des Potentials sind zusätzlich zu beachten: Ladungswechselwirkung im Nahfeld: Columbpotential weit entfernte Moleküle werden durch ihr Dipolmoment p repräsentiert. sehr weit entfernte Molekülgruppen werden durch ihr Dipol- und Quadrupolmoment Q beschrieben. Beispiel Wasser: 1. Berechnung des Dipolfeldes des H2O Moleküls 2. Berechnung der Dipol-Dipol-Wechselwirkungsenergie für zwei spezielle Stellungen der Dipole gegeneinander entlang x: entlang y: 3. Einfaches Modell für die Struktur von H2O und Summation über die nächsten Nachbarn Dipolfeld: pR 3 D ( R) 4 0 R Potential des Dipolfeldes: Dipolfeld als Gradient des Potentials: E ( R) 1 4 0 R ˆ (3 pR cos( ) p) 3 In x – Richtung: R̂ und p haben gleiche Richtung 0 1 2p also : E ( x) 4 0 R 3 Wechselwirkungsenergie: Entspricht der potentiellen Energie des Dipols im Feld des anderen: W P E E ( R) 1 4 0 R ˆ (3 pR cos( ) p) 3 p 4 0 R ˆ ˆ (3R cos( ) p) 3 W1 2P2/r3 = 0.145 eV W2 P2/r3 = 0.072 eV mit P = 6.21030 Cm r = 3.11010 m Keine 2, da p und R nicht mehr die selbe Richtung! Struktur des Wassers: Versuche folgendes einfache Modell in z dieselbe Lage nochmals, aber um 1 Zeile verschoben betrachte nur die nächsten Nachbarn Energie der nächsten Nachbarn: z-Dimension nicht gezeichnet! um ein Molekül aus dem Verband zu entfernen braucht man folgende Energie: Wentf = 2W1 + 2W2 + 2W2 Aber: nachdem einige Moleküle entfernt wurden, braucht man für den Rest weniger Energie, daher systematisches Abzählen notwendig. Abzählen in x - Richtung: Energie W1 2 W1 (N1) W1 N Moleküle pro Molekül: Beitrag zur Energie = (N1)/N W1 W1 Abzählen: in y - Richtung: Energie W2 2 W2 N W2 2N Moleküle 2 N W2 3N Moleküle Bei M Zeilen beträgt der Beitrag pro Molekühl: ( M 1) N W W 2 2 MN Analoges gilt für die Beiträge zwischen verschiedenen Lagen in z – Richtung: ( L 1) NM W2 W2 LNM Aufbau: Die Struktur wird von einer Ecke her aufgebaut: : : : ... ... ... es werden nur die Wechselwirkungsenergien für die sich links, unten und unterhalb (in z) befindlichen Moleküle frei (d.h. der Faktor 2 tritt nicht auf) Wges = W1 + W2 + W2 = 0.29 eV/H2O experimentell: es fehlen EV = 0.42 eV/H2O 0.13 eV /H2O Gase Die mittlere kinetische Energie der Teilchen wird groß gegen die Bindungsenergie. Die Moleküle werden völlig frei bewegbar, sie bilden ein Gas, das jeden ihm angebotenen Raum annimmt. Der mittlere Abstand der Teilchen, und damit die Dichte hängen davon ab, welches Volumen zur Verfügung steht!! Ideale Gas: Gas besteht aus Atomen oder Molekühlen, die sich mit statistisch verteilten Geschwindigkeiten bewegen und sich wie kleine Kugeln mit Radius r0 verhalten. Bei Stößen gelten Energie- und Impulssatz. Stöße sind vollkommen elastisch. Wechselwirkung erfolgt nur über Stöße. Beschreibung: Ideale Gasgleichung: PV=NkBT Kommt zur Anwendung, wenn r0 klein gegen den mittleren Abstand der Teilchen. Zurück zu den fehlenden 0.13 eV /H2O naiv: betrachte flüssiges Wasser als ein Gas mit Volumen V0 = 0 bei der Gas-Temperatur T0 = 0 (Moleküle sollen sich kaum bewegen) Volumsarbeit: pV = RT kinetische Energie: kT/2 W PdV pro Mol pro Freiheitsgrad und H2O H2O hat 33 Freiheitsgrade Schwerpunktsbewegung: 3 allgemeine Rotation: 3 interne Schwingungen: 3 (bei T=100°C noch nicht angeregt) insgesamt: kT + 6kT/2 = 4kT = 0.13 eV pro H2O perfekt, aber nur fast! V V0 Reales Gas: Eigenvolumen der Teilchen nicht vernachlässigbar! Korrekturen an der idealen Gasgleichung: Volumen: Atom in Volumen V=L3 Mittelpunkte der Atome können nicht näher als r an die Wand! Zwei Atome können nicht am gleichen Ort sein! Daher: Volumen für das 2 –te Atom: V2=(L-2r)3-8Va Für das 3 -te Atome: V3=(L-2r)3-2*8Va Für n -te Atome: Vn=(L-2r)3-(n-1)*8Va Summation über alle N Atome: N N Vn Vn ( L 2r ) (n 1)8Va L3 4 NVa 3 n 1 n 1 Vom Volumen b = 4NVa abziehen!! Reales Gas: Korrektur beim Druck: Bei tiefen Temperaturen oder größeren Dichten potentielle Energie aufgrund gegenseitiger Anziehung nicht vernachlässigbar! Daher Binnendruck: pb=a/V2 Daraus ergibt sich die van-der-Waals-Gleichung: a ( p 2 )(VM b) RT VM Superfluidität: Eine Flüssigkeit bezeichnet man dann als Superfluide, wenn sie an Körpern vorbeifließt, ohne eine Kraft auf diese auszuüben, oder wenn Körper, die sich in der Flüssigkeit bewegen, nicht abgebremst werden. superfluidität zeigt sich bei extrem tiefen Temperaturen dadurch, dass eine Flüssigkeit die Wände eines Becherglases emporkriecht und ihre Viskosität verliert.