x %in% y
Werbung

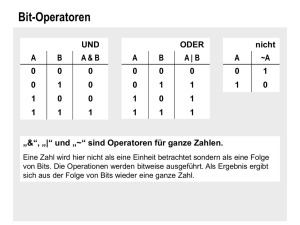
Grundlagen der R Programmiersprache Jonathan Harrington Objekte Vektor Besteht aus einem oder mehrerern Elementen x = 3 meinedatei = c(10, 20, -4) foo = c("IPSK", "Phonetik", "Schellingstr 3", 2006, "WS") Matrix Eine Zusammensetzung aus Vektoren rbind() und cbind() Logischer Vektor Besteht aus TRUE und FALSE Vektoren: Zugriff auf Elemente foo = c("IPSK", "Phonetik", "Schellingstr 3", 2006, "WS") foo[2] foo[2:4] foo[-3] Alle Elemente außer "Schellingstr 3" Elemente 2 und 5 foo[c(2, 5)] oder a = c(2, 5) foo[a] Arithmetische Funktionen werden immer parallel auf Vektoren angewendet x = c(10, 20, 30) y = c(-5, 0, 10) x * y [1] -50 0 300 Die length() Funktion wieviele Elemente in einem Vektor? length(x) [1] 3 length(y) [1] 3 length(x)==length(y) [1] TRUE Matrizen rbind(): Reihenverbindung x = c(10, 20, 30) y = c(-5, 0, 10) mat = rbind(x, y) mat [,1] [,2] [,3] x 10 20 30 y -5 0 10 Reihenanzahl nrow(mat) [1] 2 Spaltenanzahl ncol(mat) [1] 3 cbind(): Spaltenverbindung mat2 = cbind(x, y) mat2 x y [1,] 10 -5 [2,] 20 0 [3,] 30 10 Dimensionenanzahl dim(mat) [1] 2 3 Matrizen und Dimensionennamen mat2 x y [1,] 10 -5 [2,] 20 0 [3,] 30 10 Dimensionen-Namen geben: dimnames() xnamen = c("Gruppe A", "Gruppe B", "Gruppe C") ynamen = c("Erg. 1", "Erg. 2") dimnames(mat2) = list(xnamen, ynamen) mat2 Erg. 1 Erg. 2 Gruppe A 10 -5 Gruppe B 20 0 Gruppe C 30 10 Dimensionen-Namen entfernen... dimnames(mat2) = NULL mat2 [,1] [,2] [1,] 10 -5 [2,] 20 0 [3,] 30 10 Matrizen und Arithmetische Vorgänge werden wie bei Vektoren parallel durchgeführt mat [,1] [,2] [,3] x 10 20 30 y -5 0 10 mat -20 [,1] [,2] [,3] x -10 0 10 y -25 -20 -10 a [,1] [,2] [,3] [,4] 10 3 8 7 11 45 20 -1 b [,1] [,2] [,3] [,4] 20 6 16 14 22 90 40 -2 a + b [,1] [,2] [,3] [,4] 30 9 24 21 33 135 60 -3 Anwendung von Funktionen auf Matrizen mat [,1] [,2] [,3] x 10 20 30 y -5 0 10 mean(mat) [1] 10.83333 (Durchschnitt aller Elemente) Durchschnitt der Reihen apply(mat, 1, mean) x y 20.000000 1.666667 Zentralwert der Spalten apply(mat, 2, median) [1] 2.5 10.0 20.0 Zugriff auf Elemente einer Matrix mat [,1] [,2] [,3] x 10 20 30 y -5 0 10 mat[2,3] bedeutet: Reihe 2, Spalte 3 [1] 10 Nur Reihe 2 mat[2,] [1] -5 0 10 Nur Spalte 3 mat[,3] x y 30 10 Reihen: Vor dem Komma Spalten: Nach dem Komma Vektoren: Eine einzige Zahl OHNE KOMMA Zugriff auf Elemente einer Matrix bridge ist eine Matrix bridge[2:8,] Reihen 2 bis 8 bridge[,c(1,3)] Spalten 1 und 3 bridge[2:8,c(1,3)] Reihen 2 bis 8 von Spalten 1 und 3 bridge[c(2,4),1] Spalte 1 von Reihen 2 und 4 bridge[1:3,-2] Reihen 1-3 aller Spalten außer Spalte 2 Logische Vektoren 410 Vokal-Labels vowlax.l length(vowlax.l) [1] 410 table(vowlax.l) vowlax.l a E I O 126 82 170 32 Dimension-namen (die Zeiten, zu denen diese Werte vorkommen) eine 410 x 4 Matrix der F1-F4 Werte dieser Vokale zum zeitlichen Mittelpunkt F1-F4 der ersten 3 Vokale vowlax.fdat.5[1:3,] T1 T2 T3 T4 897.5 562 1768 2379 3399 1127.5 648 1463 2523 3346 1462.5 684 1274 2505 3477 die Werte dieser Vokale: vowlax.l[1:3] Wir wollen den durchschnittlichen F2 aller "a“ Vokale berechnen. Dafür werden logische Vektoren benötigt… Logischer Vektor = Ein Vektor aus TRUE und FALSE Elementen temp = c(T, F, T) temp [1] TRUE FALSE TRUE Logische Vektoren folgen einer Boolean-Logik & bedeutet "und" Das Ergebnis von T & T TRUE und [1] T TRUE ist TRUE F & F [1] F T & F [1] F | bedeutet "oder" T | T [1] T F | F [1] F T | F [1] T Klammern Material innerhalb ( ) wird zuerst bearbeitet (T & F) | T [1] TRUE ( (T | F ) [1] TRUE & (T & T) | F) Logische Vektoren, sum() und any() Wieviele T? Wieviele F? sum() vec = c(T, T, F, T, F) sum(vec) [1] 3 sum(!vec) [1] 2 Gibt es mindestens einen T? Oder mindestens einen F? any() vec2 = c(F, F, F, F) any(vec) [1] TRUE any(!vec) [1] TRUE any(vec2) [1] FALSE any(!vec2) [1] TRUE sum(any(!vec2)) [1] 1 Vergleichungs-Operator x == y x < gleicht x y? ist x weniger als y? y x %in% y != gleicht nicht > größer als <= weniger oder gleicht ist y in x enthalten? Erster Fall: y besteht aus einem Element x = c(10, 20, 30) y = 20 x == y [1] FALSE TRUE FALSE x == 20 [1] FALSE TRUE FALSE Vergleichungs-Operator Zweiter Fall. x und y sind zueinander parallel (und bestehen daher aus der selben Anzahl von Elementen) x = c(10, 20, 30) y = c(9, 50, 30) x == y [1] FALSE FALSE TRUE Vergleichungs-Operator %in% labs = c("I", "E", "O", "O", "O","I", "E") labs %in% "E" [1] FALSE (kommt "E" in labs vor?) TRUE FALSE FALSE FALSE FALSE labs %in% c("I", "E") [1] TRUE TRUE (kommen "E" oder "I" in labs vor?) TRUE FALSE FALSE FALSE TRUE TRUE TRUE TRUE Dasselbe: y = c("I", "E") labs %in% y [1] TRUE TRUE FALSE FALSE FALSE Zugriff auf Elemente durch [logische Vektoren] x = c(23, 5, 45, -10, 11) lvec = x > 20 [1] TRUE FALSE TRUE FALSE FALSE > x[lvec] bedeutet: die Elemente in x, für die lvec TRUE ist [1] 23 45 x[!lvec] [1] 5 -10 11 Meine Freunde freunde = c("Paul", "Karin", "Elke", "Georg", "Peter") Die Dauer (Min.) um in die Arbeit zu kommen zeit = c(50, 11, 35, 41, 12) Welche Dauern sind größer als 40? temp = zeit > 40 temp [1] TRUE FALSE FALSE TRUE FALSE Was ist (a) die Bedeutung (in Wörtern) und (b) das Ergebnis von: freunde[temp] (a) Bedeutung: die Freunde, die länger als 40 Minuten brauchen, um in die Arbeit zu kommen. (b) [1] "Paul" "Georg" freunde = c("Paul", "Karin", "Elke", "Georg", "Peter") zeit = c(50, 11, 35, 41, 12) Schreiben Sie R-Befehle für: Welche Freunde brauchen 41 Minuten, um in die Arbeit zu kommen? temp = zeit == 41 freunde[temp] [1] "Georg" oder freunde[zeit == 41] [1] "Georg" Schreiben Sie R-Befehle für: Welcher Freund braucht am längsten? Hier muss auch die max() Funktion verwendet werden: y = c(10, 20, 30) max(y) [1] 30 temp = zeit == max(zeit) freunde[temp] [1] "Paul" Oder freunde[zeit == max(zeit)] [1] "Paul" R-Befehle für: welcher Freund braucht zwischen 25 und 45 Minuten? (die Freunde, die mehr als 25 Minuten brauchen) & (die Freunde, die weniger als 45 Minuten brauchen) temp = (zeit > 25) & (zeit < 45) freunde[temp] [1] "Elke" "Georg" R-Befehle für: Wieviele Freunde brauchen weniger als 40 Minuten? sum() temp = zeit < 40 sum(temp) [1] 3 Oder sum(zeit < 40) Gibt es Freunde, die mehr als 45 Minuten brauchen? any() temp = zeit > 45 any(temp) [1] TRUE oder in einer Zeile: any(zeit > 45) [1] TRUE dim(bridge) [1] 13 3 Die Elemente von Reihe 1, die größer als 30 sind (logischer Vektor verwenden) temp = bridge[,1] > 30 bridge 0 1 2 3 4 5 6 7 8 9 10 11 12 Mon Tues Wed 9 1 0 35 1 1 68 5 7 94 4 27 90 27 68 76 28 87 62 62 108 28 76 111 27 90 57 4 94 28 5 68 6 1 35 0 1 9 0 bridge[temp,1] 1 2 3 4 5 6 35 68 94 90 76 62 Alle Reihen von bridge, für die die Werte in Reihe 1 größer als 30 sind bridge[temp,] Mon Tues Wed 1 35 1 1 2 68 5 7 3 94 4 27 4 90 27 68 5 76 28 87 6 62 62 108 Logische Vektoren Ein Vektor von 410 VokalEtikettierungen vowlax.l table(vowlax.l) x = c(10, 15, 18) mean(x) [1] 14.33333 F2- Durchschnitt aller "a" Vokale? temp = vowlax.l == "a" mean(vowlax.fdat.5[temp,2]) [1] 1437.214 Eine Matrix der F1-F4 Werte zum zeitlichen Mittelpunkt vowlax.fdat.5 dim(vowlax.fdat.5) Seite 31 von Aufgaben 1 (Vektoren) und 2 (Matrizen) von: A sketch of the R Programming language and environment (in Harrington, J. forthcoming, The Phonetic Analysis of Speech Corpora. Blackwell): doc, pdf. http://www.phonetik.unimuenchen.de/~jmh/lehre/emur.htm