p - Softwaretechnik und Programmiersprachen

Aussagenlogik
Schnelldurchlauf
Michael Leuschel
Softwaretechnik und Programmiersprachen
27/10/15
Lecture 3
Teil 1:
Sprache (Syntax)
27/10/15
Bestandteile
n 
Atomare Aussagen (atomic propositions)
n 
Entweder wahr oder falsch (Wahrheitswert, truth
value auf Englisch; true oder false)
n 
n 
zwei-wertig
Wahrheitswert einer komplexen Aussage:
n 
bestimmt von Wahrheitswerten der Bestandteile
it rains and it is cold
27/10/15
it rains
it is cold
Alphabet der Aussagenlogik
n 
Junktoren
n 
n 
n 
n 
n 
n 
Atomare Aussagen
n 
n 
Und (Konjunktion): ∧
Oder (Disjunktion): ∨
Wenn (Implikation): →
←
Not (Negation):
¬
Äquivalenz ⟺, Exklusives Oder, . . .
Bezeichner:
p
q
(
)
Klammerung
n 
27/10/15
Klammern
rains ...
Well Formed Formulas (WFF)
n 
n 
alle atomare Aussagen sind in der Menge WFF
Wenn α und β in WFF sind, dann sind folgende
Formeln auch in WFF:
n 
n 
n 
n 
n 
n 
(¬ α)
(α ∧ β)
(α ∨ β)
(α → β)
Keine anderen Forrmeln sind in WFF
Anmerkung: α, β sind Meta-Variablen (ausserhalb der
Aussagenlogik)
27/10/15
Präzedenz
1. Negation ¬ bindet am stärksten
2. Dann kommen ∧ und ∨
3. Am schwächsten bindet →
Anstatt:
n 
(((¬ p) ∧ (¬ q)) → ((¬ p) ∨ (¬ q)))
kann man auch dies schreiben:
n 
n 
27/10/15
(¬ p ∧ ¬ q) → (¬ p ∨ ¬ q)
¬p∧¬q → ¬p∨¬q
Teil 2:
Semantik der Aussagenlogik
Interpretationen, Modelle, logische
Schlussfolgerung
27/10/15
Wahrheitswert einer Formel
n 
n 
Zuweisung: WFF↝ Wahrheitswert
Junktoren:
n 
n 
n 
n 
feste Bedeutung
Bsp: true ∧ false ergibt false
Wahrheitstabellen (truth tables)
Atomare Aussagen:
n 
n 
27/10/15
egal (wahr oder falsch)
(die Logik kümmert sich um die Form, nicht den
Inhalt !)
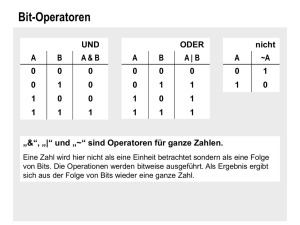
Wahrheitstabellen
α
β
¬α
α∧ β
α∨ β
α→ β α⇔ β
true
true
false
true
true
true
true
true
false
false
false
true
false
false
false
true
true
false
true
true
false
false
false
true
false
false
true
true
27/10/15
Interpretationen und Modelle
n 
Eine Interpretation v ist eine Abbildung von atomaren
Aussagen nach {true,false}
Beispiel: v(p) = true, v(q) = false
n 
Erweiterung von v auf WFF mit den Wahrheitstabellen:
Beispiel: v(p ∨ q) = ?
n  1. Berrechne v for Bestandteile:
n 
n 
v(p) = true, v(q) = false
2. Wende Wahrheitstabelle an: true ∨ false = true
n 
v(p ∨ q) = true
Für v’(p) = false, v’(q) = false: v’(p ∨ q) = false
n 
Interpretation v ist ein Modell für α gdw v(α) = true
27/10/15
Übungen:
n 
n 
v(p) = true,v(q) = false
v’(p) = false,v’(q) = false
n 
n 
n 
n 
n 
n 
n 
27/10/15
v(p ∧ (q ∨ (¬p) )) =
v(p → (p → q )) =
v’(p → (p → q )) =
v(p ∨ (¬p)) =
v’(p ∨ (¬p)) =
v(p ∧ (¬p)) =
v’(p ∧ (¬p)) =
Übungen: Lösung
n 
n 
v(p) = true,v(q) = false
v’(p) = false,v’(q) = false
n 
n 
v(p ∧ (q ∨ (¬p) )) false
n 
n 
v(p)
v(q ∨ (¬p) )
true
n 
v(p ∧ (q ∨ (¬p) )) = false
v(p → (p → q )) = false
v’(p → (p → q )) = true
v(p ∨ (¬p)) = true
v’(p ∨ (¬p)) = true
false
v(q)
false
27/10/15
v(¬p) false
n 
n 
v(p)
true
v(p ∧ (¬p)) = false
v’(p ∧ (¬p)) = false
Satisfaction, Tautology,
Contradiction
n 
Eine Formel α ∈ WFF ist
erfüllbar (satisfiable) gdw es mindestens
ein Modell gibt
n  unerfüllbar oder ein Widerspruch
(unsatisfiable or a contradiction) gdw es
kein Modell gibt
n  eine Tautologie gdw alle Interpretationen
auch Modelle sind
n 
p ∨ (¬p)
27/10/15
p ∧ (q ∨ (¬p) )
p ∧ (¬p)
Consequence and
Equivalence
n 
Zwei Formeln α and β sind logisch
äquivalent, α ≡ β, gdw sie die gleichen
Modelle haben (d.h. gleiche Wahrheitstabelle)
(p ∧ q) ≡ (q ∧ p)
(p → q) ≡ (¬p ∨ q)
n 
Die Formel α ist eine logische Konsequenz
von β, β ⇒ α, gdw jedes Modell von β auch
ein Modell von α ist
p ⇒ (q ∨ p)
27/10/15
oft
anstatt ⇒
Erweiterung für Mengen
n 
Eine Interpretation v ist ein Modell für eine
Menge S an Formeln in WFF gdw sie ein
Modell für jede Formel in S ist
v(p)=true,
n 
v ist ein Modell von {(p ∨ q), (¬p → ¬q)}
Eine Menge A ist eine logische Konsequenz
einer anderen Menge B, B ⇒ A,
gdw jedes Modell von B auch ein Modell von
A ist
{p} ⇒ {(p ∨ q), (¬p → ¬q)}
27/10/15
Beispiel
Ja
{p → q , ¬q} ⇒ {¬p}
?
auch Modell von {¬p}
v(p)=true,
v(q)= true
v(p)=true,
v(q)=false
v(p)= false,
v(q)= true
4 mögliche Interpretationen
27/10/15
v(p)= false,
v(q)= false
einziges Modell von
{p → q , ¬q}
Ein anderes Puzzle
Ein Zettel sagt die
Wahrheit der
andere nicht.
?
In dieser Zelle befindet
sich eine Prinzessin und
ein Tiger in der anderen
Zelle
27/10/15
?
?
?
In einer der Zellen
befindet sich eine
Prinzessin und in der
anderen ein Tiger
Erläuterungen
n 
Notationen:
n 
n 
n 
Unterschied zwischen ⇔ und ≡
n 
n 
n 
p ⇔ q ist eine erfüllbare Formel
p ≡ q ist keine Formel (und ist falsch)
Unterschied zwischen → und ⇒
n 
n 
n 
α ⇔ β steht für (α → β) ∧ (β → α)
α ← β steht für (β → α)
p → ¬p ist eine erfüllbare Formel
p ⇒ ¬p ist keine Formel (und ist falsch)
→, ⇔ sind Junktoren ≡, ⇒ sind math.
(Meta-)Aussagen über Formeln
27/10/15
Achtung: mathematische
Logik vs Sprachgebrauch
n 
n 
Kommutativität: p ∧ q ≡ q ∧ p
Aber:
n 
n 
n 
n 
He got scared and he killed the intruder.
Er bekam Angst und tötete den Eindringling.
He killed the intruder and he got scared.
Er tötete den Eindringling und bekam Angst.
(kausale und temporale Bedeutung von
“und”)
n 
Implikation
Falls 1 = 2 dann bin ich Bundespräsident.
27/10/15
Zusammenfassung
n 
Syntax der Aussagenlogik
n 
n 
Semantik der Aussagenlogik
n 
n 
n 
27/10/15
WFF
Wahrheitstabellen, Interpretationen, Modelle
Erfüllbarkeit, Tautologie, Widerspruch
logische Äquivalenz und Konsequenz