Experimentalphysik 3

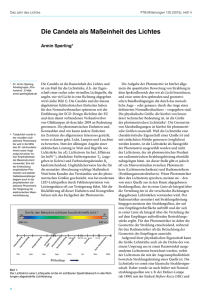
Optik
Experimentalphysik 3
Dr. Georg von Freymann
20. Oktober 2009
Matthias Blaicher
Dieser Text entsteht wärend der Vorlesung „Klassische Experimentalphysik 3“
im Wintersemester 2009/2010 an der Universität Karlsruhe, a.k.a KIT. Wie die
Vorlesung, so ist auch dieses Skript in zwei Teile „Optik“ sowie „Thermodynamik“
geteilt.
1
1 WAS IST LICHT
1 Was ist Licht
Licht kann als elektro-magnetische Welle oder als Quanten (Photon) beschrieben werden
(Dualität). Ein LASER verscheidener Wellenlänge und gleicher Leistung kann unterschiedlich
hell erscheinen, man muss also unterscheiden ob eine Lichtquelle hell ist (physikalische Größe)
oder ob sie hell erscheint (physiologische Größe). Wegen der offenkundigen Wichtigkeit des
subjektiven Eindrucks sind photometrische Größen von Bedeutung.
1.1 Photometrische Größen
Basiseinheiten der Optik
Lichtstärke 1 Candela (Cd), 1 Candela ist die Lichtstärke mit der ein 6001000 Quadratmeter
eines schwarzen Strahlers bei der Temperatur des beim Druck von 101325 Kilogram
durch Meter und durch Sekundequadrat erstarten Platins senkrecht zu seiner Oberfläche
leuchtet.
Abgeleiteten photometrische Größen
Lichtstrom 1 Lumen (lm) = Cd * sr, 1 Lumen ist gleich dem Lichtstrom, den eine punktförmige Lichtquelle der Lichtstärke 1 Cd gleichmäßig nach allen Richtungen in den
Raumwinkel 1 sr ( = 4π) aussendet.
Beleuchtungsstärke 1 Lux (lx) = lm * m−2 . Über das planksche Strahlungsgesetz (siehe
6.2, schwarze Strahler) kann 1 Cd mit der physikalischen Größe 1 Watt in Verbindung
gebracht werden. Bei einer Frequenz von 540 THz (=555 nm Wellenlänge) gilt
1 Cd =
1 W
683 sr
Spektrale Empfindlichkeit des Auge (hell-adaptiert) Bild 1, sichtbares Licht
Beispiel
λ = 555 nm
λ = 750 nm
physikalischen
W
1m
2
W
1m
2
physiologisch
683 Lx
0, 1 Lx
Wärend bei der Beleuchtungsindustrie phisiologische Größen im Vordergrund stehen, wollen
wir uns im Folgenden auf die physikalischen Größe konzentrieren.
Energieflussdichte ist verknüpft mit der elektromagnetischen Welle, und gegeben durch den
~ mit S
~=E
~ ×H
~ [s] = W2 . Bei elektromagnetischen Wellen gilt im
Poynting-Vektor S
m
Vakuum
~
r
E µ0
=
= Vakuum-Impedanz Z0 = 376 Ω = Z0
~
ε0
H 2
1.2 Kohärenz von Licht
1 WAS IST LICHT
und somit mit
2 r ε
~ ~ 0
S = E µ0
~s k ~k
~ mit der Frequenz ω, so oszilliert auch auch S.
~ Mittelt man über diese
Oszilliert E
zeitliche Oszillation, dann spricht man von der Intensität I des Lichts.
1.2 Kohärenz von Licht
Licht breitet sich in Form elektromagnetischer Wellen aus. Eine ideale ebene Welle, sogenanntes kohärentes Licht, könnte z.B. sein:
~ =E
~ 0 cos ~k · ~r − ωt
E
Veranschaulichung
Ort, bei fester Zeit
Bild 2, Amplitude über Zeit, bei festem ~r
Bild 3, Amplitude über
Das Licht aus Lasern kommt idealen ebenen Wellen sehr nahe. Das Licht einer Glühlampe
weist hingegen eine endliche Kohärenzzeit und eine endliche Koherenzlänge auf.
Bild 4, Glühlampe, Amplitude über Zeit
Kohärenzzeit =
Kohärenzlänge
Lichtgeschwindigkeit
1.2.1 Experiment: Michelson Interferometer
Bild 5, Strahlengang
Bild 6, Intensität über ∆x, für Laser und Weißlicht
3