r - Institut für Experimentelle Physik
Werbung

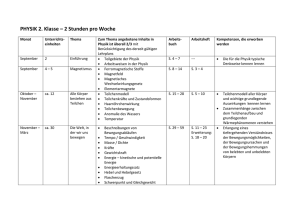
PHYS3100 Grundkurs IIIb für Physiker Othmar Marti Experimentelle Physik Universität Ulm [email protected] Vorlesung nach Tipler, Gerthsen, Alonso-Finn, Halliday Skript: http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 Übungsblätter und Lösungen: http://wwwex.physik.uni-ulm.de/lehre/gk3b-2003-2004/ueb/ue# 23. Oktober 2003 Universität Ulm, Experimentelle Physik http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Übungsgruppen Gruppe 1 Montag, 8-10, O25/202 Dr. Bernd Heise, ungerade Wochen Gruppe 2 Montag, 8-10, O25/202 Dr. Bernd Heise, gerade Wochen Gruppe 3 Montag, 8-10, N24/252 Oliver Crasser, ungerade Wochen Gruppe 4 Montag, 8-10, N24/252 Oliver Crasser, gerade Wochen Gruppe 5 Montag, 14-16, ? Holger Schieferdecker, ungerade Wochen Gruppe 6 Montag, 8-10, N24/254 Holger Schieferdecker, gerade Wochen Universität Ulm, Experimentelle Physik 1 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Elektrostatische Kräfte Auslenkung zweier mit identischer q Ladung geladener Kugeln. Universität Ulm, Experimentelle Physik 2 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Henry CAVENDISH (1731 - 1810) Universität Ulm, Experimentelle Physik 3 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Ladungsarten • Zwei Ladungen ziehen sich an, wenn sie verschiedener Art sind (positiv und negativ oder negativ und positiv) • Zwei Ladungen stossen sich ab, wenn sie gleichnamig sind (positiv und positiv oder negativ und negativ) Universität Ulm, Experimentelle Physik 4 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Elektrostatische Kräfte und Gravitationskräfte Genaue Messungen zeigen, dass für Elektronen die elektrostatischen Kräfte etwa 4.1681 × 1042 mal stärker als die Gravitationskräfte sind. Gravitation: FG(r) = 10−71N m2r −2. m2 G r2e = 6.670 × Elektrostatische Kraft: FE (r) = = 2.3068 × 10−28N m2r −2. 2 1 qe 4π²0 r 2 ³ ´ −31 kg 2 9.1091×10 2 10−11 Nkgm2 r2 = 1 2 4π8.8544×10−12 C 2 Nm = 5.5345 × ³ ´2 1.6021×10−19 C r2 Die Gravitationskräfte können also nur beobachtet werden, da die Ladungen sich im Mittel sehr genau kompensieren. Universität Ulm, Experimentelle Physik 5 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Coulombgesetz F1 q1 = q2 F2 (1) r12 q1 · q2 ~ ~ (~ F r) = K 2 r12 r12 (2) K= 1 4π²0 −12 ²0 = 8.8544 × 10 Universität Ulm, Experimentelle Physik (3) C2 N m2 (4) 6 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Charles Augustin de COULOMB (1736 - 1806) Universität Ulm, Experimentelle Physik 7 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Coulomb-Gesetz erraten ~ (~ • F r ) ist ein Vektorfeld. ~ ist • Der mathematische Fluss dieses Vektorfeldes durch ein Flächenelement dA ~ ·F ~ (~ ~ die Richtung der Normalen zu dΦ(~ r ) = dA r), wobei die Richtung von A diesem Flächenelement ist. 2 • RR Der gesamte Fluss durch die Kugeloberfl äche A(r) = 4πr ist durch Φ(r) = RR ~ (~ ~ gegeben. dΦ(~ r) = A F r)dA A ~ (~ • Da das Problem kugelsymmetrisch ist, kann F r) nicht von der Richtung abhängen und muss radial sein. Damit kann die Kraft vor das Integral genommen werden. RR • Φ(r) = F (r) A dA = 4πr 2F (r) ~ unabhängig von r sein soll, so muss die Kraft • Wenn der Fluss des Vektorfeldes F umgekehrt proportional zu r 2 sein. Universität Ulm, Experimentelle Physik 8 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Coulomb-Gesetz Das Coulombsche Gesetz lautet 1 q · q ~ r 1 2 12 ~ F (~r) = (5) 2 r 4π²0 r12 12 Universität Ulm, Experimentelle Physik 9 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Ladungserhaltung Ladungen können nur paarweise entstehen (jeweils die gleiche negative und positive Ladung). Die Gesamtladung in einem abgeschlossenen System ist konstant. Universität Ulm, Experimentelle Physik 10 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Elektrische Felder in der Natur V E/ N = C m −2 Stromleitung in Wohnhäusern 10 Radiowellen 10−1 Atmosphäre 102 Sonnenlicht 103 Unter einer Gewitterwolke 104 In einer Röntgenröhre 106 Laser bis 1012 Am Ort des Elektrons im Wasserstoffatom 6 · 1011 Auf der Oberfläche eines Urankerns 2 · 1021 Universität Ulm, Experimentelle Physik 11 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Feldlinien Feldlinien. Links von einer positiven Ladung, rechts von einer negativen Ladung. Die Feldlinien zeigen von der positiven Ladung zu der negativen Ladung. Universität Ulm, Experimentelle Physik 12 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Michael FARADAY (1791 - 1867) Universität Ulm, Experimentelle Physik 13 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Feldlinien für zwei positive Ladungen Feldlinien bei zwei gleichen positiven Ladungen. Universität Ulm, Experimentelle Physik 14 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Feldlinien zweier entgegengesetzter Ladungen Feldlinien bei einer positiven Ladung und einer vom Betrage her gleichgrossen negativen Ladung. Universität Ulm, Experimentelle Physik 15 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Konventionen 1. Elektrische Feldlinien beginnen bei positiven Ladungen und enden bei negativen Ladungen. 2. Um eine einzelne Punktladung herum sind alle Feldlinien kugelsymmetrisch verteilt 3. Die Anzahl der Feldlinien, die von positiven Ladungen ausgehen, oder auf negativen Ladungen enden, ist proportional zu der Grösse der Ladung. 4. An jedem Punkt des Raumes ist die Feldliniendichte proportional zur Feldstärke in diesem Punkt. 5. In grosser Entfernung wirkt ein System von Ladungen wie eine einzige Punktladung, deren Grösse der Gesamtladung des Systems entspricht. 6. Feldlinien schneiden sich nicht. Universität Ulm, Experimentelle Physik 16 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Elektrostatisches Feld ~ (~ F r) ~ E(~ r) = lim q→0 q (6) Wir definieren Das elektrische Feld der Ladung Q ist durch ~ r) = E(~ 1 Q ~r12 2 r 4π²0 r12 12 (7) gegeben. Universität Ulm, Experimentelle Physik 17 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Elektrische Felder von Ladungsverteilungen N X N X 1 qi ~r − ~ri ~ ~ E(~r) = E(~r − ~ri) = 2 |~ 4π² |~ r − ~ r | r − ~ri| 0 i i=0 i=0 (8) ∆Q(~r) ρel(~r) = lim ∆V →0 ∆V (9) ~ r0) = E(~ 1 4π²0 Universität Ulm, Experimentelle Physik ZZZ ρel(~r) ~r0 − ~r dV 2 |~r0 − ~r| |~r0 − ~r| (10) 18 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Berechnung der eingeschlossenen Ladung Universität Ulm, Experimentelle Physik 19 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Carl Friedrich GAUSS (1777 - 1855) Universität Ulm, Experimentelle Physik 20 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Approximation von beliebigen Oberflächen durch Kugelsegmente. Approximation einer kontinuierlichen Ladungsverteilung durch Punktladungen. Universität Ulm, Experimentelle Physik 21 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Dipole Kräfte auf einen Dipol im homogenen elektrischen Feld Universität Ulm, Experimentelle Physik 22 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Geladene Kugelschale Universität Ulm, Experimentelle Physik 23 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Robert Jemison VAN DE GRAAFF (1901 - 1967) Universität Ulm, Experimentelle Physik 24 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Kugelschale E-Feld einer Kugelschale 2 E(x) E 1.5 2 Er = Q/(4π ε0 r ) 1 Er = 0 0.5 0 0 2 4 6 8 10 r Universität Ulm, Experimentelle Physik 25 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 geladene Kugel E-Feld einer homogen geladenen Kugel 2 Er = Qr/(4π ε0 R2) Ek(x) E 1.5 2 Er = Q/(4π ε0 r ) 1 0.5 0 0 2 4 6 8 10 r Universität Ulm, Experimentelle Physik 26 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Integrationsfläche Universität Ulm, Experimentelle Physik 27 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Elektrisches Feld ungleich geladener Flächen Universität Ulm, Experimentelle Physik 28 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Elektrisches Feld gleich geladener Flächen Universität Ulm, Experimentelle Physik 29 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Inneres eines Leiters Leiter haben in ihrem Inneren keine statischen elektrischen Felder. Universität Ulm, Experimentelle Physik 30 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Integrationsfläche Universität Ulm, Experimentelle Physik 31 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Existenz der potentielle Energie Eine potentielle Energie existiert, wenn • Die Arbeit W (~r1 → ~r2)unabhängig vom Weg ist. • Die Arbeit für jede geschlossene Bahn null ist. ~ × F~ (~r) = 0 für alle ~r •∇ Universität Ulm, Experimentelle Physik 32 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Beziehungen /q F~ (~r) R − F~ d~ry x ~ −∇Epot −→ ←− ·q ~ (~r) E ~ r − Ed~ y R x ~ −∇U /q Epot (~r) −→ ←− U (~r) = U (~r) ·q (11) Universität Ulm, Experimentelle Physik 33 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Potential eines Kreisringes Kreisring: Potential entlang der Symmetrieachse 0.6 U(x) 0.5 U 0.4 0.3 0.2 0.1 0 0 2 4 6 8 10 x Universität Ulm, Experimentelle Physik 34 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Potential einer Kreisscheibe Kreis: Potential entlang der Symmetrieachse 2 U(x) U 1.5 1 0.5 0 0 2 4 6 8 10 x Universität Ulm, Experimentelle Physik 35 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Potential einer Ebene Homogen geladene Ebene: Potential 2 U(x) 1 U 0 -1 -2 -3 -4 -2 0 2 4 x Universität Ulm, Experimentelle Physik 36 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Potential einer Kugelschale Homogen geladene Kugelschale: Potential 2 U(x) U 1.5 1 0.5 0 0 2 4 6 8 10 x Universität Ulm, Experimentelle Physik 37 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Potential einer Linienladung Homogene Linienladung: Potential 2 U(x) 1 U 0 -1 -2 -3 1 2 3 4 5 6 7 8 9 10 x Universität Ulm, Experimentelle Physik 38 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Kapazität: Integrationsfläche Integrationsoberfläche an der Grenze Metall-Vakuum Universität Ulm, Experimentelle Physik 39 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Plattenkondensator Geometrie eines Plattenkondensators. Wir betrachten auf beiden Seiten eine Fläche A die jeweils in eine unendlich ausgedehnte Fläche eingebettet ist. Universität Ulm, Experimentelle Physik 40 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Parallelschaltung von Kondensatoren Parallelschaltung von Kondensatoren Universität Ulm, Experimentelle Physik 41 http://wwwex.physik.uni-ulm.de/Lehre/gk3b-2003-2004 23. Oktober 2003 Reihenschaltung von Kondensatoren Reihenschaltung oder Serienschaltung von Kondensatoren Universität Ulm, Experimentelle Physik 42