Einführung in die Astronomie und Astrophysik I

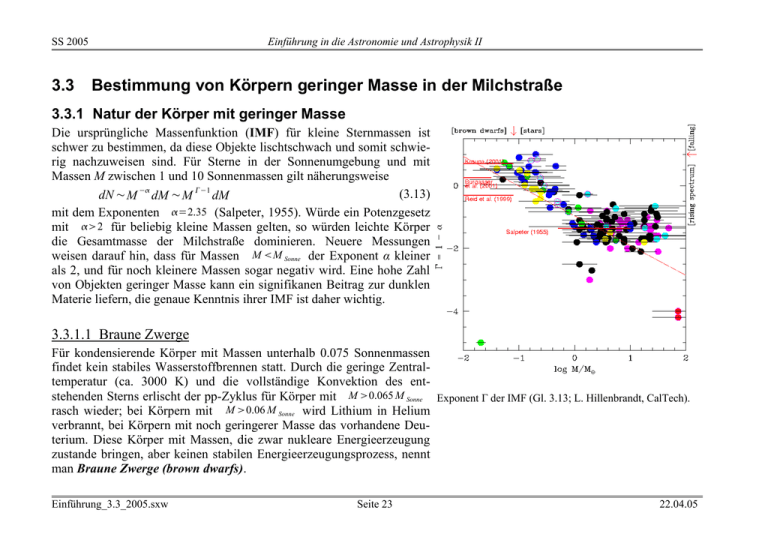
SS 2005
3.3
Einführung in die Astronomie und Astrophysik II
Bestimmung von Körpern geringer Masse in der Milchstraße
3.3.1 Natur der Körper mit geringer Masse
Die ursprüngliche Massenfunktion (IMF) für kleine Sternmassen ist
schwer zu bestimmen, da diese Objekte lischtschwach und somit schwierig nachzuweisen sind. Für Sterne in der Sonnenumgebung und mit
Massen M zwischen 1 und 10 Sonnenmassen gilt näherungsweise
(3.13)
dN ~M ­ dM ~M ­1 dM
mit dem Exponenten =2.35 (Salpeter, 1955). Würde ein Potenzgesetz
mit 2 für beliebig kleine Massen gelten, so würden leichte Körper
die Gesamtmasse der Milchstraße dominieren. Neuere Messungen
weisen darauf hin, dass für Massen M M Sonne der Exponent α kleiner
als 2, und für noch kleinere Massen sogar negativ wird. Eine hohe Zahl
von Objekten geringer Masse kann ein signifikanen Beitrag zur dunklen
Materie liefern, die genaue Kenntnis ihrer IMF ist daher wichtig.
3.3.1.1 Braune Zwerge
Für kondensierende Körper mit Massen unterhalb 0.075 Sonnenmassen
findet kein stabiles Wasserstoffbrennen statt. Durch die geringe Zentraltemperatur (ca. 3000 K) und die vollständige Konvektion des entstehenden Sterns erlischt der pp-Zyklus für Körper mit M 0.065 M Sonne Exponent Γ der IMF (Gl. 3.13; L. Hillenbrandt, CalTech).
rasch wieder; bei Körpern mit M 0.06 M Sonne wird Lithium in Helium
verbrannt, bei Körpern mit noch geringerer Masse das vorhandene Deuterium. Diese Körper mit Massen, die zwar nukleare Energieerzeugung
zustande bringen, aber keinen stabilen Energieerzeugungsprozess, nennt
man Braune Zwerge (brown dwarfs).
Einführung_3.3_2005.sxw
Seite 23
22.04.05
SS 2005
Einführung in die Astronomie und Astrophysik II
Man erkennt Braune Zwerge an spektralen Signaturen im nahen Infrarot,
insbesondere an Absorptionslinien von Molekülen und Alkaliatomen. Für
sie wurden extra die neuen Spektralklassen L und T eingeführt. Da
empfindliche Messungen in diesen Spektralbereichen aufwendige
technische Einrichtungen benötigen, sind Braune Zwerge erst Mitte der
Neunziger Jahre entdeckt worden. Mittlerweile sind einige Hundert
Braune Zwerge entdeckt worden.
Farb-Helligkeitsdiagramm (J,K) und Entwicklungslinien
von Braunen Zwergen (Burgasser et al.)
Spektrum eines Braunen Zwerges des Spektraltyps T.
Einführung_3.3_2005.sxw
Seite 24
22.04.05
SS 2005
Einführung in die Astronomie und Astrophysik II
3.3.1.2 Extrasolare Planeten
Körper mit noch geringerer Masse erzeugen keine Kernreaktionen mehr und haben einen planetenähnlichen Charakter. Die
Grenzmasse liegt bei etwa 0.013 Sonnenmassen oder etwa 13 Jupitermassen. Die Radien der Planeten von Jupitergröße
entspricht den Radien von späten M-Zwergen und Braunen Zwergen. Die Oberflächentemperaturen sind – mit Ausnahme von
sehr jungen Planeten – von der Einstrahlung eines Zentralsterns und damit vom Radius der Planetenbahn abhängig.
Extrasolare Planeten werden bislang vorwiegend durch ihre Gravitation nachgewiesen; direkte Abbildungen sind wegen des
hohen Kontrasts zum Zentralstern ausgesprochen schwierig.
Gegenwärtig sind über 150 extrasolare Planeten“kandidaten“ nachgewiesen, vorwiegend durch Messung der
Radialgeschwindigkeit. Die Extrasolar Planets Encyclopedia (http://www.obspm.fr/encycl/encycl.html) hält die neuesten
Entdeckungen zu extrasolaren Planeten bereit.
Darstellung der Größen der Sonne (links), eines M-Zwergs, zweier Brauner Zwerge (L und T) und Jupiter (rechts). Bild: Caltech.
Einführung_3.3_2005.sxw
Seite 25
22.04.05
SS 2005
Einführung in die Astronomie und Astrophysik II
3.3.2 Nachweismethoden
3.3.2.1 Microlensing
Als Microlensing bezeichnet man den Effekt der Lichtablenkung einer entfernten Quelle durch einen sich zwischen Quelle
und Beobachter befindenden massiven Körper, speziell im Bereich der Masse M = 10-8 ... 102 MSonne. Dabei spielt das
Gravitationsfeld des Körpers die Rolle einer "Linse". Die beobachtete Wirkung ist eine Ablenkung des Bildes der Quelle von
der Position ohne Linse, eine Deformation des Bildes und u. U. Mehrfachbilder.
Ursache des Linseneffekts ist die Raumkrümmung durch die Gravitationskraft. Nach der Allgemeinen Relativitätstheorie
ergibt sich das Weltlinienelement ds in der Nähe einer Punktmasse, ausgedrückt in Schwarzschild-Koordinaten (r,θ,ϕ) zu
−1
(
 R 
 R 
ds = − 1 − S  c 2 dt 2 + 1 − S  dr 2 + r 2 dθ 2 + sin 2 θ dϕ 2
r 
r 


Dabei ist
2GM
RS =
c2
der Schwarzschild-Radius der Linse mit der Masse M.
2
)
(3.14)
(3.15)
Lichtfelder breiten sich längs Geodätischer Linien aus, für die gilt: ds 2 = 0 . Integriert man (3.14) geeignet über die Zeit und
betrachtet man das Problem in einem Koordinatensystem, für welches θ fest ist, so läßt sich die Trajektorie eines Lichtstrahls
durch z. B. eine gegenseitige Abhängigkeit von r
und ϕ darstellen. Eine Lösung ist
r
b
α
RS
b
ϕ
= sin ϕ +
(1 − cosϕ )
(3.16)
b
r
Dabei spielt b die Rolle eines "impact"-Parameters.
Zum Microlensing.
Einführung_3.3_2005.sxw
Seite 26
22.04.05
SS 2005
Einführung in die Astronomie und Astrophysik II
Die Änderung des Sehwinkels ist gegeben mit
R
δα = S (1+ cos α ) .
b
(3.17)
Betrachtet man eine Quelle, die sich im Abstand Ds befindet, in der Nähe einer (punktförmigen) Linse, welche den Abstand Dl
hat, so ergeben wenigstens zwei Lösungen für Lichtwege zum Beobachter. Im dem Fall, wo Beobachter, Linse und Quelle auf
einer Linie liegen, ist das Bild sogar ein Ring ("Einsteinring"). Die Abstände der Bilder r von der Richtung zur Linse im
Bogenmaß ergeben sich aus der Gleichung
r 2 − r0 r − R02 = 0
(3.18)
wobei r0 der "wahre" scheinbare Abstand der Quelle zur Linse,
(D − Dl )
4GM (Ds − Dl )
= 2RS s
R02 =
Ds Dl
Ds Dl
c2
(3.19)
der Radius des Einsteinrings im Bogenmaß ist. Hieraus ergibt sich für die Positionen der Bilder relativ zur Linse
r± = 1 r0 ± r02 + 4R02 
2 

Die Intensität der Bilder wird um einen Faktor A verstärkt:
A± = 1 1±
2
(3.20)
2 R02 + r02
(3.21)
r0 4R02 + r02
Die folgenden Abbildungen zeigen Positionen und relative Intensitäten der Bilder. Man beachte, dass bei geringen Abständen
die Helligkeit der Quelle um mehrere Größenordnungen von der Linse verstärkt werden kann.
Einführung_3.3_2005.sxw
Seite 27
22.04.05
SS 2005
Einführung in die Astronomie und Astrophysik II
Positionen der Bilder
6
1 .10
3
4
100
Verstärkungsfaktor
Scheinbarer Abstand [E. R.]
Intensität der Bilder
4
1 .10
2
10
1
0
0.1
0.01
2
0
1
r_plus
r_minus
klassisch
2
3
Wahrer Abstand [E. R.]
4
5
1 .10
0
1
I_plus
I_minus
Abbg. 3.2.4-1: r als Funktion von r0
Einführung_3.3_2005.sxw
3
2
3
Wahrer Abstand [E. R.]
4
5
Abbg. 3.2.4-2: Intensität als Funktion von r0.
Seite 28
22.04.05
SS 2005
Einführung in die Astronomie und Astrophysik II
Abbg. 3.2.4-3: Lichtkurven (links) und Sternkarten (rechts) des OGLE-Surveys für Mikrolinsen
(http://sirius.astrouw.edu.pl/~ogle/).
Einführung_3.3_2005.sxw
Seite
22.04.05
SS 2005
Einführung in die Astronomie und Astrophysik II
Die Dauer ∆T eines Ereignisses hängt ab von der Geschwindigkeit vl der Linse relativ zur Verbindungslinie BeobachterQuelle in der dazu senkrechten Ebene. Sie kann abgeschätzt werden mit
∆T =
2 Dl R0
vl
(3.22)
Die Entfernung DS zu einer galaktischen Quelle - i. A. ein Hintergrundstern - läßt sich der Abstand mit photometrisch einer
Präzision von ca. 20% bestimmen. Bei einer extragalaktischen
Quelle, z. B. bei Sternen in den Magellanschen Wolken, ist der
Abstand mit ähnlicher relativer Genauigkeit bekannt. Die Linse
hingegen ist i. a. unsichtbar.
Man kennt daher mit (3.19) einen Zusammenhang zwischen
Masse, Abstand Dl und Geschwindigkeit der Linse, aber keine
dieser Größen unabhängig. Bei der Beobachtung eines Ereignisses muss man daher aus der Lichtkurve und aus den Parametern der Quelle auf die Linsenmasse schliessen.
Bei einem Ereignis von 40 Tagen Dauer in Richtung des
Milchstraßenzentrums (8.5 kpc) ergibt sich der schraffierte Bereich für das Verhältnis von Abstand und Masse der Linse in
der Abbildung 3 (links). Dies gilt, wenn man eine Geschwindigkeit der Linse von 100 ... 300 km/s zugrunde legt.
Abb. 3.2.4-4: Masse-Abstandsdiagramm.
Einführung_3.3_2005.sxw
Seite
22.04.05
SS 2005
Einführung in die Astronomie und Astrophysik II
Weitere Schlüsse auf die Natur von Linse und Quelle kann man anhand sogen. Anomalien der Lichtkurven schließen.. Da die
Lichtablenkun ein geometrischer Effekt ist, ist sie unabhängig von der Wellenlänge. Ist der scheinbare Durchmesser des
Quellstern aufgelöst, so kann die Mitte-Rand-Variation der Effektivtemperatur auf der Sternscheibe zu Abweichungen der
Lichtkurven als Funktion der Wellenlänge führen.
Abbg. 3.2.4-5: Mitte-Rand-Variation von Sternen im I- und V-Band.
Einführung_3.3_2005.sxw
Seite
22.04.05
SS 2005
Einführung_3.3_2005.sxw
Einführung in die Astronomie und Astrophysik II
Seite
22.04.05
SS 2005
Einführung_3.3_2005.sxw
Einführung in die Astronomie und Astrophysik II
Seite
22.04.05
SS 2005
Einführung in die Astronomie und Astrophysik II
Andere, drastischere Modifikationen treten auf, wenn die Linse eine Doppelquelle ist. Etwa 10% der bisher beobachteten
Ereignisse sind Doppelquellen. Beträgt ihr scheinbarer Abstand ein Vielfaches der jeweiligen Einstein-Radii, so erzeugt jede
Linse eine eigene Aufhellung der Quelle, die Effekte überlagern. Ist der Abstand geringer, so entsteht eine gemeinsame
Kaustik, die für drastische Sprünge in der Helligkeit sorgt.
Gemeinsame Kaustik gleich schwerer Linsen.
Einführung_3.3_2005.sxw
Lichtkurven.
Seite
22.04.05
SS 2005
Einführung_3.3_2005.sxw
Einführung in die Astronomie und Astrophysik II
Seite
22.04.05
SS 2005
Einführung in die Astronomie und Astrophysik II
Ein besonderer Fall tritt ein, wenn bei einer
Binärlinse ein Partner eine sehr geringe Masse
hat, d. h., eins substellare Komponente ist. In
diesem Fall ist das Ereignis aufgrund der
masseärmeren Komponente von sehr kurzer
Dauer, die Intensitätsänderung aber durchaus
von vergleichbarer Größenordnung.
Einführung_3.3_2005.sxw
Seite
22.04.05
SS 2005
Einführung in die Astronomie und Astrophysik II
3.3.2.2 Nachweis von gebundenen Körpern geringer Masse
Bei gebundenen Körpern kleiner Masse handelt es sich in der Regel um Begleiter eines normalen Einzelsterns. Aus
verschiedenen Gründen waren solche Körper bis vor kurzem praktisch unbeobachtbar und wenig war über ihre Eigenschaften
bekannt, insbesondere über ihre Masseverteilung N(M). Das Problem ist häufig die Masse und die alles beherrschende
Strahlung des Hauptkörpers des Systems, des Sterns.
Die folgenden Techniken der Detektion von gebundenen Körpern geringer Masse werden eingesetzt:
• Astrometrische Messung der Reflex-Eigenbewegung des Hauptkörpers,
• Spektroskopische Messung der Reflex-Radialgeschwindigkeit des Hauptkörpers,
• Okkultation des Hauptkörpers durch den Begleiter,
• Direkte Abbildung des Begleiters,
• Korrelierte Mikrolinsenereignisse.
Diese werden im folgenden besprochen.
Astrometrische Reflex-Eigenbewegung:
In einem System aus zwei Körpern mit Massen M1 und M2 bewegen sich
beide auf elliptischen Bahnen mit großen Halbachsen a1, a2 um den
gemeinsamen Schwerpunkt mit der Periode P. Dabei gilt:
M2
M 1a1 = M 2 a2
M1 + M 2 =
4π (a1 + a2 )
G
P2
2
3
,
(3.20)
a2
a1
M1
Ist M2 gegenüber M1 vernachlässigbar, so gilt näherungsweise
Einführung_3.3_2005.sxw
Seite
22.04.05
SS 2005
Einführung in die Astronomie und Astrophysik II
M 23
4π 2 a13 2
=
M1
2
G P
(3.23)
Diese Gleichung erfordert auf der rechten Seite ausschließlich Größen, die den Hauptkörper betreffen. Man kann aus der
abgeschätzten Masse des Hauptkörpers (meist ein Hauptreihenstern), der gemessenen großen Halbachse seiner Bahn und der
Periode die Masse des Begleiters ermitteln. Aus der astrometrische Messung läßt sich der Inklinationswinkel und die
Exzentrizität bestimmen, wenn die Reflexbahn des Hauptkörpers und ihr zeitlicher Ablauf hinreichend genau gemessen
werden kann. Das macht die Bestimmung der Begleitermasse sehr sicher.
Bei bekannter Parallaxe p des Systems, Angabe der Periode P in Jahren sowie von M1 in Sonnenmassen erhält man aus der
Messung von a1 in Bogensekunden die Begleitermasse M2 in Massen der Erde mit
M 23
Planet
4π 2 a13
2
=
M
1
G p3 P2
Masse [MSonne]
Jupiter
Saturn
Uranus
Neptun
9.5 10-4
2.9 10-4
4.4 10-5
5.1 10-5
.
Umlaufzeit
[yr]
11.9
29.6
84.7
165.5
(3.24)
Gr. HA [AU] Gr. HA Sonne Gr. HA Sonne bei
[AU]
10 pc [10-3 arcsec]
5.2
4.9 10-3
0.49
-3
9.6
2.8 10
0.28
-4
19.3
8.5 10
0.09
30.1
1.5 10-3
0.15
V1 [m / s]
12.3
2.8
0.30
0.27
Das Planetensystem, insbesondere die großen Planeten, gibt auch für die Sonne Anlaß zu einer Reflexbewegung. Dabei
bewegt sich der Schwerpunkt auf Bahnen von der Größenordnung von 5 10-3 Astronomischen Einheiten (s. Tabelle). Dies
entspricht etwa einem Sonnenradius, d. h. der gemeinsame Schwerpunkt befindet sich noch innerhalb der Sonne in der Nähe
der Sonnenoberfläche! Beobachtet man unser Sonnensystem aus einer Entfernung von 10 pc, so ergibt sich eine
Einführung_3.3_2005.sxw
Seite
22.04.05
SS 2005
Einführung in die Astronomie und Astrophysik II
Reflexbewegung von etwa 500 Mikro-Bogensekunden, mit Perioden von 11 Jahren und darüber. Diese Zahlen führen einem
die Anforderungen an die instrumentelle Präzision bei astrometrischen Detektionen kleiner Körper vor Augen.
Bis heute sind noch keine substellaren Körper mit M < 90 MJupiter auf diese Weise entdeckt worden. Trotzdem ist die Methode
wegen ihres absoluten Charakters von besonderem Interesse. Mit Interferometern auf der Erde (PTI, VLTI und Keck) sowie
im Weltraum (SIM) hofft man, die erforderliche astrometrische Präzision zu erreichen.
Einführung_3.3_2005.sxw
Seite
22.04.05
SS 2005
Einführung in die Astronomie und Astrophysik II
Reflexbewegung in Radialgeschwindigkeiten:
Ähnlich wie bei der Reflexbewegung misst man mit der Radialgeschwindigkeitsmethode den Einfluß des Begleiters auf den
Hauptkörper und sucht nach der radialen Komponente dieser Bewegung durch den Dopplereffekt. Die dabei auftretenden
maximalen Geschwindigkeiten lassen sich für die Sonne ebenfalls aus der obigen Tabelle ersehen. Es handelt sich bei
Körpern von Planetenmassen (MJupiter = 1.9 1027 kg) und bei sonnenähnlichen Sternen offenbar um Effekte von wenigen m/s,
und mit Perioden von vielen Jahren.
Seit Ende der 80er Jahre gab es mehrere Programme, bei welchen die Spektren einiger Dutzend naher Sterne über viele Jahre
hinweg vermessen wurden mit dem Ziel, Reflexbewegungen von einigen Dutzend m/s nachzuweisen. Zu diesem Zweck
wurden spezielle Spektrographen mittlerer Auflösung und sehr hoher Stabilität gebaut. Insbesondere muss die absolute
Kalibration über viele Jahre hin mit hoher Genauigkeit erhalten bleiben. Dabei haben sich zwei Methoden durchgesetzt:
1. Absolute Eichung des Spektrographen an simultan mit der Beobachtung gemessenen Spektren von Laborquellen
2. Standardsterne bekannter Radialgeschwindigkeit, welche zeitlich stabil bleiben
Heute wird eine Kombination beider Methoden verwendet. Als Laborquellen eignen sich Th-Ar-Lampen sowie in den
Strahlengang eingebrachte Jodküvetten, wobei dem Sternspektrum eine Vielzahl von Moleküllinien des J2 überlagert werden.
Die Bestimmung der Begleitermasse erfordert eine wiederholte Messung der Radialgeschwindigkeit des Hauptkörpers. Bei
einer charakteristischen periodischen Schwankung bestimmt man Periode P und Geschwindigkeitsamplitude K. Legt man die
Sternenmasse nach seinem Spektraltyp zugrunde, so lässt sich der Radius der Begleiterbahn nach dem 3. Keplerschen Gesetz
ermitteln
a 23 =
GM 1 2
P
2
4π
(3.25)
Die Bahngeschwindigkeit des Planeten ergibt sich aus dem Gravitationsgesetz:
V2 =
GM 1
a2
(3.26)
und damit die Masse des Planeten aus der Impulserhaltung mit
Einführung_3.3_2005.sxw
Seite
22.04.05
SS 2005
Einführung in die Astronomie und Astrophysik II
M 2 = M1
V1
V2
, mit
V1 =
K
sin i
(3.27)
In der Tat entspricht die gemessene Geschwindigkeitsamplitude der wahren Geschwindigkeit des Hauptkörpers nur bis auf
einen Faktor sin i, wobei i der Inklinationswinkel der Bahnnormalen zur Richtung zum Beobachter ist. Die eigentliche
Bestimmungsgröße ist daher M 2 sin i .
Bis in die Mitte der 90er Jahre ist man davon ausgegangen, dass Planeten mit nennenswerter Masse keine sternennahe Bahnen
haben können, da sie sich nicht in unmittelbarer Nähe zum Stern hätten bilden können. Daher musste man davon ausgehen,
dass nur geduldige Arbeit und lange Beobachtungsprogramme erfolgreich massearme Körper werden nachweisen können.
Umso erstaunter war man, als mit einem Begleiter von etwa (0.5 sin i) Jupitermassen um den Stern 51 Pegasi der erste
extrasolare Planet um einen sonnenähnlichen Stern nachgewiesen wurde, der eine Umlaufperiode von nur 4.23 Tagen hatte!
Dieser Orbit hat eine Halbachse von nur 0.05 AU, weit näher am Zentralstern als für möglich gehalten.
Durch Analyse vorhandenen Datenmaterials und mit der Gewinnung neuer Beobachtungen ist bis heute die Entdeckung von
ca. 40 extrasolaren Planeten im Bereich von 0.1 bis 10 Jupitermassen in Orbits bis ca. 3 AU gelungen. Die meisten befinden
sich auf sehr sternennahen Bahnen, deren Erklärung ein wichtiges Thema der Hydrodynamik geworden ist.
Modell eines entstehenden Planeten.
Geschwindigkeitskurve von 51 Peg.
Einführung_3.3_2005.sxw
Seite
22.04.05
SS 2005
Einführung in die Astronomie und Astrophysik II
Kreuzdispergiertes Echelle-Spektrum eines Sterns.
Einführung_3.3_2005.sxw
Seite
22.04.05
SS 2005
Einführung in die Astronomie und Astrophysik II
Keck HIRES Spektrograph.
Einführung_3.3_2005.sxw
Seite
22.04.05
SS 2005
Einführung in die Astronomie und Astrophysik II
Messung von Radialgeschwindigkeiten mit
Hilfe eines dem Sternspektrum überlagerten
Molekülspektrum des J2. Oberste Linie:
Spektrum
des
Jod-Moleküls
mit
Absorptionslinien durch Vibrations- und
Rotationszuständen, die einem elektronischem Übergang überlagert sind. Zweite
Linie: Spektrum des Sterns. Die breiteren
Linien sind durch die höhere Temperatur in
der Sternatmosphäre bedingt. Dritte Linie:
gemessenes
Spektrum
(Punkte)
der
Überlagerung
beider
oberer
Linien,
verschmiert durch die Auflösung des
Spektrographen, und modelliertes Spektrum
mit gefitteter Verschiebung des Sternspektrums gegenüber den Linien des J2. Punkte
ganz unten: um einen Faktor 10 überhöhte
Residuen der Differenz Messung - Modell.
Quellen:
G. Marcy, San Francisco State University, "Discovery of Extrasolar Planets",
http://www.physics.sfsu.edu/~gmarcy/planetsearch/planetsearch.html
S. Udry, Univ. Genf, " Extrasolar Planet Search Programmes", http://obswww.unige.ch/~udry/planet/planet.html
J. Schneider, Obs. de Paris, " Extrasolar Planets Encyclopedia", http://www.obspm.fr/encycl/encycl.html
Einführung_3.3_2005.sxw
Seite
22.04.05
SS 2005
Einführung in die Astronomie und Astrophysik II
Okkultationen:
Befindet sich die Sehlinie zum Hauptkörper in der Bahnebene des Begleiters, so kann dieser den Hauptkörper bedecken und
somit eine charakteristische Schwankung der Helligkeit hervorrufen. Ähnlich den Bedeckungsveränderlichen. Dieser Effekt
ist selten und vermutlich sehr klein. Bei einer Bedeckung durch den Jupiter würde die Helligkeit der Sonne um ca. 1%
schwanken, dies ist aber innerhalb der Nachweisgrenze präziser photometrischer Methoden. Bislang konnte ein Transit an
einem Planetensystem um dem G0-Stern HD 209458, welches schon vorher bekannt war, mit einer Amplitude von 0.017 mag
nachgewiesen werden. Neuerdings gelingen Transitnachweise auch mit den Microlensing-Experimenten.
Schema eines Planeten-Transits.
Einführung_3.3_2005.sxw
Seite
22.04.05
SS 2005
Einführung in die Astronomie und Astrophysik II
Direkte Abbildung:
Die Leuchtkraft eines Sterns in einem Planetensystem übersteigt je
nach Wellenlänge die eines Planeten um viele Größenordnungen.
Dabei ist ein Teil des Lichtes des Planeten reflektiertes
Sternenlicht, ein anderer Teil die je nach Oberflächentemperatur
mehr oder weniger langwellige thermische Eigenstrahlung des
Begleiters. In der näheren Sonnenumgebung entsprechen die
Bahnradien von sonnensystemähnlichen Planeten einige Zehntel
bis Hundertstel Bogensekunden (Jupiter: 0.5 arcsec bei 10 pc).
Eine direkte Abbildung eines Planeten erfordert daher die Messung
sehr großer Helligkeitsunterschiede von Objekten mit sehr
geringem Winkelabstand. Dies ist mit herkömmlichen
erdgebundenen Teleskopen unmöglich.
Trotzdem gibt es gewichtige Gründe für direkte Beobachtungen, da
nur durch die Analyse des Lichtes von Planeten Aussagen über die
physikalische Beschaffenheit ihrer Oberflächen gemacht werden
können. Es gibt daher mehrere Projektvorschläge zu deren
Realisierung.
Die Grafik zeigt die geschätzte Rückstreuung und Eigenstrahlung
der Erde und der Sonne, dabei ist die Erde typischerweise 7 bis 10
Größenordnungen dunkler als die Sonne. Im Spektrum der Erde
lassen sich Signaturen für Moleküle finden. Davon gilt die Signatur
von O3 als sicheres Anzeichen von Leben. Liessen sich ähnliche Beobachtungen auf anderen Sternen machen, so könnte man
dort ggf. Leben nachweisen.
Um das Licht des Planeten zu messen, muss das Sternenlicht um viele Größenordnungen unterdrücht werden. Eine
Möglichkeit, das mit Hilfe eines Interferometers zu tun, wurde von R. Bracewell 1979 vorgeschlagen ("NullingInterferometrie").
Einführung_3.3_2005.sxw
Seite
22.04.05
SS 2005
Einführung_3.3_2005.sxw
Einführung in die Astronomie und Astrophysik II
Seite
22.04.05
SS 2005
Einführung in die Astronomie und Astrophysik II
Terrestrial Planet Finder (TPF): dieses Konzept eines Weltraum-Interferometers soll mit Hilfe der
nulling - Technik das Licht des zentralen Sterns unterdrücken und nahe Planeten sichtbar machen. Das
Licht eines Planeten kann spektroskopisch auf Vorhandensein von Spuren einer Sauerstoff-Atmosphäre
untersucht werden. Die Simulation des mit einem Interferometer gewonnenen Bildes unseres
Planetensystems ist rechts dargestellt. Die vier inneren Planeten, Merkur bis Mars, sind zu sehen.
Einführung_3.3_2005.sxw
Seite
22.04.05
SS 2005
Einführung_3.3_2005.sxw
Einführung in die Astronomie und Astrophysik II
Seite
22.04.05