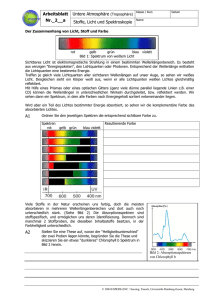
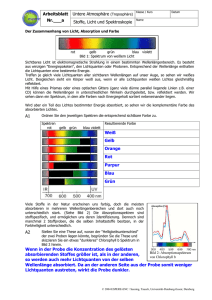
ZIP - FreiDok - Albert-Ludwigs

Nematische Elastomere:
Untersuchungen zur Kopplung
der flüssigkristallinen Phase an
das Polymernetzwerk
Dissertation zur Erlangung der Doktorwürde
der Fakultät für Chemie, Pharmazie und Geowissenschaften
der Albert-Ludwigs-Universität Freiburg im Breisgau
Dezember 2006
vorgelegt von
Stefanie Müller
geboren in Völklingen
Vorsitzender der Promotionsausschusses:
Prof. Dr. Georg E. Schulz
Dekan:
Prof. Dr. Andreas Bechthold
Referent:
Prof. Dr. Heino Finkelmann
Korreferent:
Prof. Dr. Eckhard Bartsch
Tag der Bekanntgabe des Prüfungsergebnisses:
08.02.2006
Die vorliegende Arbeit entstand in der Zeit von März 2004 bis Dezember 2006
am Institut für Makromolekulare Chemie der Albert-Ludwigs-Universität
Freiburg im Breisgau
„So, finished!“
R. Zentel zum Abschluss seines Vortrages, ILCC 2006
Posterpräsentationen
Stefanie Müller, H. Finkelmann
Coupling between Order and Dimension in Nematic Elastomers
34. Arbeitstagung Flüssigkristalle, Freiburg im Breisgau , 29.-31.03.2006
Stefanie Müller, H. Finkelmann
Coupling between Order and Dimension in Nematic Elastomers
International Liquid Crystal Conference, Keystone (CO), USA, 02.-07.07.2006
Vorträge
Stefanie Müller, H. Finkelmann
Thin films of photocrosslinked nematic side chain elastomers
SFB 428 Doktorandenkolleg, Waldau, 22.06.2006
Inhaltsverzeichnis
1. EINLEITUNG UND ZIELSETZUNG........................................................ 1
2. GRUNDLAGEN ............................................................................................ 3
2.1. Physikalische Eigenschaften isotroper Netzwerke .............................................. 3
2.1.1. Mechanische Eigenschaften ................................................................................. 3
2.1.2. Doppelbrechung .................................................................................................... 7
2.2. Niedermolekulare Flüssigkristalle .......................................................................... 8
2.3. Flüssigkristalline Polymere..................................................................................... 10
2.4. Flüssigkristalline Seitenkettenpolymere ............................................................. 11
2.4.1. odd-even-Effekt...................................................................................................... 11
2.4.2. Knäuelanisotropie ............................................................................................... 12
2.4.3. Steuerung der Knäuelanisotropie und Nullkopplung................................... 13
2.5. Flüssigkristalline Elastomere.................................................................................. 15
2.6. Eigenschaften flüssigkristalliner Elastomere ...................................................... 17
2.6.1. Ordnungsgrad...................................................................................................... 17
2.6.2. Doppelbrechung .................................................................................................. 19
2.6.3. Bestimmung des Ordnungsgrades aus der Doppelbrechung ...................... 23
2.6.4. Landau-de Gennes Theorie................................................................................ 25
2.7. Dielektrische Eigenschaften von Flüssigkristallen ............................................ 32
3. SYNTHESE NEMATISCHER POLYMERE UND ELASTOMERE ... 35
3.1. Nomenklatur der Monomere .................................................................................. 35
3.2. Polymersynthesen ..................................................................................................... 36
3.2.1. Polymere mit unterschiedlicher Vernetzerkonzentration............................. 37
3.2.2. Copolymere mit reduzierter Kopplung ........................................................... 38
3.2.3. E-Feld-sensitive Copolymere............................................................................. 40
3.3. Herstellung dünner Monodomänenfilme ............................................................ 43
3.3.1. Probenpräparation als dünne Filme ................................................................. 43
3.3.2. Orientierung im Magnetfeld.............................................................................. 44
3.3.3. Vernetzungsreaktion........................................................................................... 45
3.4. Präparation der Proben zur Untersuchung im elektrischen Feld .................... 46
3.5. Synthese der Mesogene............................................................................................ 48
3.5.1. M3OCH3............................................................................................................... 48
3.5.2. M4OCH3............................................................................................................... 49
3.5.3. M3CN/M4CN....................................................................................................... 50
4. ERGEBNISSE UND DISKUSSION......................................................... 51
4.1. Prinzipien der Auswertung ..................................................................................... 51
4.1.1. Relative Länge als Funktion des Ordnungsgrades ........................................ 52
4.1.2. Elastischer Modul................................................................................................ 54
4.2. Einfluss der Vernetzerkonzentration auf die Kopplung................................... 58
4.2.1. Orientierungs- und thermisches Verhalten der linearen Polymere............. 58
4.2.2. Untersuchung der Netzwerke ........................................................................... 60
4.3. Beeinflussung der Kopplung durch Copolymerisation .................................... 70
4.3.1. Charakterisierung der linearen Polymere ....................................................... 70
4.3.2. Untersuchung der Elastomere........................................................................... 75
4.4. E-Feld-sensitive Polymere und Elastomere.......................................................... 90
4.4.1. E-Feld-sensitives Polymer/Elastomer mit C4-Spacer..................................... 90
4.4.2. E-Feld-sensitives Copolymer/elastomer .......................................................... 95
5. ZUSAMMENFASSUNG.......................................................................... 101
6. EXPERIMENTELLER TEIL ..................................................................... 103
6.1. Synthese der Monomere ........................................................................................ 103
6.1.1. 4-But-3-enyloxybenzoesäure (M4COOH)...................................................... 103
6.1.2. 4-But-3-enyloxybenzoesäure-4-methoxyphenylester (M4OCH3).............. 105
6.1.3. 4-But-3-enyloxybenzoesäure-4-cyanophenylester (MC4CN) ..................... 106
6.1.4. 4-Allyloxybenzoesäure (M3COOH) ............................................................... 107
6.1.5. 4-Allyloxybenzoesäure-4-methoxyphenylester (M3OCH3) ....................... 109
6.1.6. 4-Allyloxybenzoesäure-4-cyanophenylester (M3CN).................................. 110
6.2. Synthese des Vernetzers ........................................................................................ 111
6.3. Synthese der linearen Polymere........................................................................... 111
6.3.1. Zusammensetzung ............................................................................................ 112
6.3.2. Durchführung der Synthese ............................................................................ 112
6.4. Präparation der dünnen Filme .............................................................................. 113
6.4.1. Vorbereitung der Glasplatten .......................................................................... 113
6.4.2. Präparation der dünnen Polymerproben....................................................... 113
6.4.3. Orientierung der Polymerproben im Magnetfeld ........................................ 113
6.4.4. Herstellung der freistehenden Elastomerfilme............................................. 114
6.5. Präparation der Proben zur Untersuchung im elektrischen Feld .................. 114
6.6. Untersuchungs- und Auswertmethoden und dazugehörige Geräte ............. 115
6.6.1. Thermoelastik-Messungen............................................................................... 116
6.6.2. Doppelbrechungsmessungen .......................................................................... 117
6.6.3. Spannungs-Dehnungs-Messungen................................................................. 120
6.6.4. Röntgenmessungen........................................................................................... 121
6.6.5. Weitere Geräte, Untersuchungsmethoden und Materialien....................... 121
6.7. Gefahren- und Sicherheitshinweise.................................................................... 124
7. LITERATUR ............................................................................................... 131
1. Einleitung und Zielsetzung
Die nematisch-isotrope Phasenumwandlung flüssigkristalliner Elastomere kann mit
der Landau-de Gennes-Theorie[1-5] beschrieben werden. Dabei handelt es sich um
einen rein phänomenologischen Ansatz, der auf der Landau-Theorie[6] basiert,
welche Phasenumwandlungen zweiter Ordnung beschreibt. In der Landau-Theorie
wird die Freie Energiedichte in einer Reihe nach dem Ordnungsparameter
entwickelt. Dieser Reihenentwicklung werden in der Modifikation nach de Gennes
einige Terme hinzugefügt, welche die Eigenschaften der flüssigkristallinen Phase
und des Netzwerks einbeziehen. So gelangt man zu einer Formulierung für die Freie
Energiedichte, die auf die Phasenumwandlung flüssigkristalliner Elastomere
anwendbar ist. Zur Beschreibung der Kopplung der flüssigkristallinen Phase an das
Polymernetzwerk wird eine Kopplungskonstante eingeführt. Außerdem wird
angenommen, dass sowohl die Kopplungskonstante als auch der Young-Modul
linear abhängig von der Dichte der Vernetzungspunkte in einer Probe sind[5].
In der nematischen Phase weicht die Knäuelkonformation der Polymerkette von der
sphärischen Konformation in der isotropen Phase ab[7-12]. Grund hierfür ist die
parallele
Ausrichtung
der
Mesogenlängsachsen,
die
durch
die
Dispersionswechselwirkung der Mesogene untereinander zustande kommt. Die
Richtung der Deformation bezogen auf den Direktor hängt von der Länge der
Spacerkette zwischen Polymerrückgrat und Mesogen ab (odd-even-Effekt)[13-18].
Untersuchungen von Guo et al.[19] zeigten, dass eine sphärische Konformation des
Polymers in der flüssigkristallinen Phase durch die Einbindung zweier Mesogene
erreicht werden kann, die einzeln betrachtet eine entgegengesetzte Deformation des
Knäuels bewirken.
Flüssigkristalline Polymere, die Mesogene mit dielektrischer Anisotropie enthalten,
können im elektrischen Feld orientiert werden. Es wird vermutet, dass dies bei
1
Einleitung und Zielsetzung
vernetzten Proben mit positiver Kopplung bei Präparation zwischen zwei Elektroden
mit definiertem Abstand nicht möglich ist, da die mit der Orientierung verbundene
Längenänderung der Probe aufgrund der Fixierung durch die Vernetzungspunkte
und dem festen Abstand zwischen den beiden Elektroden nicht erfolgen kann.
Um zu überprüfen, inwieweit die Annahmen von de Gennes bezüglich der
Vernetzungsdichte auf das Verhalten realer Seitenkettenelastomere anwendbar sind,
soll eine systematische Untersuchung der Kopplungskonstanten an einer Reihe von
Elastomeren mit unterschiedlichem Vernetzergehalt durchgeführt werden.
Weiterhin soll durch systematische Variation des Konzentrationsverhältnisses zweier
Mesogene, die eine entgegengesetzte Ausrichtung ihrer Längsachsen im Bezug auf
das Polymerrückgrat aufweisen, eine Reihe von Polymeren und Elastomeren
synthetisiert werden, deren Kopplung stetig bis auf eine Nullkopplung reduziert
wird. Die Vernetzerkonzentration soll dabei konstant gehalten werden, um die
Abhängigkeit der Kopplungskonstanten vom Gehalt der Mesogene genau
untersuchen zu können.
Durch den Einbau von Mesogenen mit dielektrischer Anisotropie soll ein Elastomer
synthetisiert werden, das im elektrischen Feld orientiert werden kann. Es soll
zunächst die Vermutung überprüft werden, dass eine Orientierung eines Elastomers
mit positiver Kopplung im elektrischen Feld nicht möglich ist. Anschließend soll auf
der Grundlage der gewonnenen Ergebnisse zur Nullkopplung ein E-Feld-sensitives
Elastomer
mit
Nullkopplung
untersucht werden.
2
synthetisiert
und
sein
Orientierungsverhalten
2. GrundlagenFormel-Kapitel 2 Abschnitt 2
In diesem Kapitel werden die theoretischen Grundlagen, die zum Verständnis der
Arbeit wichtig sind, beschrieben. Nach einer Betrachtung der physikalischen
Eigenschaften isotroper Netzwerke erfolgt die Beschreibung der Grundzüge
niedermolekularer
Charakteristika
Schwerpunkt
flüssigkristalliner
flüssigkristalliner
stellt
hierbei
die
Phasen.
Polymere
Behandlung
Anschließend
und
wird
Elastomere
der
auf
die
eingegangen.
Knäuelkonformation,
der
Doppelbrechung und der Landau-de Gennes-Theorie der nematisch-isotropen
Phasenumwandlung dar. Abschließend wird auf die dielektrischen Eigenschaften
von flüssigkristallinen Substanzen eingegangen.
2.1. Physikalische Eigenschaften isotroper Netzwerke
Oberhalb ihrer Klärtemperatur verhalten sich flüssigkristalline Elastomere wie
isotrope
Netzwerke,
weshalb
hier
auf
deren
physikalische
Eigenschaften
eingegangen wird. Die mechanischen Eigenschaften isotroper Netzwerke werden in
erster Linie durch den Elastizitätsmodul beschrieben. Charakteristisch für die
optischen Eigenschaften ist die durch eine angelegte Spannung induzierte
Doppelbrechung, deren Ursache in der teilweisen Ausrichtung der Polymerkettensegmenten liegt.
2.1.1. Mechanische Eigenschaften[20, 21]
Die Elastizität von Polymernetzwerken beruht im Gegensatz zur Elastizität anderer
Festkörper auf deren Streben nach maximaler Entropie. Dies wird anhand folgender
Ableitung deutlich.
3
Grundlagen
Wird auf ein isotropes Netzwerk eine uniaxial wirkende Kraft ausgeübt, so wird es
deformiert. Die Kraft f lässt sich als Ableitung der Freien Energie F nach der
absoluten Ausdehnung L beschreiben.
∂F
f =  
 ∂L T ,V
(2.1)
Die Freie Energie F des Systems ist gegeben durch
F = U − T ⋅S
(2.2)
wobei U die Innere Energie des Systems, S die Entropie und T die Temperatur sind.
Damit wird unter Vernachlässigung der Volumenänderung und bei konstanter
Temperatur die aufzuwendende Kraft zur Deformation eines Netzwerks zu
∂U 
 ∂S 
f = 
 −T  
 ∂L T
 ∂L T
(2.3)
erhalten.
Bei den meisten Festkörpern, bei denen durch die Deformation Bindungswinkel und
–längen verändert werden, dominiert dabei der erste Term dieses Ausdruckes,
welcher der Ableitung der Inneren Energie nach der Länge entspricht. Er beschreibt
die übliche Form der Energieelastizität.
Bei Polymernetzwerken kann die Änderung der Inneren Energie allerdings
vernachlässigt werden, da hier die entscheidende Größe für die Änderung der Freien
Energie die Änderung der Entropie ist. Durch Deformation eines Elastomers wird
eine Veränderung der statistischen Knäuelkonformation der Polymere induziert.
Dies führt zu einer Entropieverringerung, da die Polymerketten nur noch eine
geringere Zahl von Konformationen einnehmen können. Nach der BoltzmannStatistik ist diese Verringerung der Konformationsmöglichkeiten mit einer
Entropieabnahme verbunden. Dadurch entsteht eine entropische Rückstellkraft, die
der angelegten Deformationskraft entgegenwirkt und bei hohen Dehnungen zu einer
Erhärtung des Elastomers führt. Wird die Temperatur unter konstanter Deformation
erhöht, nimmt diese Kraft zu, da durch die größere thermische Energie auch die
4
Grundlagen
Kettenbeweglichkeit erhöht und somit die Deformation des Polymerknäuels kleiner
wird.
Nach Entfernen der äußeren Kraft wird durch das Streben der Polymerknäuel nach
einem Zustand höchster Entropie der Ausgangszustand wieder hergestellt. Die
Deformation eines Netzwerks ist daher vollständig reversibel.
Anhand des affinen Netzwerkmodells lassen sich die Eigenschaften eines Elastomers
ableiten. In diesem Modell ist das Netzwerk aus Ketten aufgebaut, die aus frei
beweglichen Segmenten bestehen. Die End-zu-End-Vektoren der Ketten sind im
spannungsfreien Zustand isotrop verteilt. Wird eine mechanische Spannung
angelegt, ordnen sie sich. Die Lage der Vernetzungspunkte ändert sich dabei affin
mit der makroskopischen Deformation. Da von einem konstanten Volumen
ausgegangen wird, ändert sich durch eine Dehnung der Probe neben ihrer
ursprünglichen Länge auch die ursprüngliche Querschnittsfläche.
Die Dehnung λ bezeichnet die Dehnung in Zugrichtung z, λzz und stellt den
Quotienten aus der eigentlichen Länge L und der Ausgangslänge L0 dar.
λ = λzz =
L
L0
(2.4)
Senkrecht zur Zugrichtung z ändern sich die Dimensionen um den Faktor (1/λ)1/2.
λxx = λyy =
1
λ
(2.5)
Das bedeutet, die Querschnittsfläche nimmt um den Faktor 1/λ ab.
A=
A0
λ
(2.6)
Die Änderung der Dimensionen bei Dehnung eines Netzwerks sind in Abbildung 2.1
dargestellt.
5
Grundlagen
1λ
1
1 λ
1
1 λ
1
λ
1
Abbildung 2.1
Dimensionsänderung bei Dehnung eines Netzwerks
Die wahre Spannung ist der Quotient der auf die Probe wirkende Kraft f und der
Querschnittsfläche A. Für sie ergibt sich somit
σw =
f
f
=
λ
A A0
(2.7)
Der Faktor f/A0 wird auch als Nominalspannung σnom bezeichnet. Beide Größen
können mit Hilfe der Kautschuktheorie folgendermaßen beschrieben werden.
σ w = σ nom ⋅ λ =
kB ⋅ T ⋅ N
ρ ⋅ R ⋅T
⋅ ( λ 2 − λ −1 ) =
⋅ ( λ 2 − λ −1 ) = G ⋅ ( λ 2 − λ −1 )
V
MC
(2.8)
Dabei sind kB die Boltzmannkonstante, T die Temperatur, N/V die Anzahl der
Netzketten pro Volumen, ρ die Dichte, R die allgemeine Gaskonstante und MC das
mittlere Netzkettenmolekulargewicht.
Der Vorfaktor von Gleichung (2.8) kann zum Schermodul G zusammengefasst
werden. Als charakteristische Größe eines Netzwerks hängt dieser stark von der
Vernetzungsdichte bzw. dem mittleren Netzkettenmolekulargewicht ab. Je höher die
Vernetzungsdichte bzw. je niedriger das mittlere Netzkettenmolekulargewicht ist,
desto höher ist der Schermodul.
Zur Formulierung des Elastizitätsmoduls E muss die wahre Spannung σw nach der
relativen Längenänderung λ abgeleitet werden[21].
6
Grundlagen
E=
∂σ w ρ ⋅ R ⋅ T
=
⋅ ( 2 ⋅ λ − λ −2 )
∂λ
MC
(2.9)
Bei kleinen Dehnungen (λ≈1) nimmt der Elastizitätsmodul das Dreifache des Wertes
des Schermoduls an. Außerdem kann bei kleinen Dehnungen die Zunahme der
Spannung mit der Dehnung als linear angenommen werden. Die Steigung der
Geraden der Auftragung von σw gegen λ entspricht dem Elastizitätsmodul.
2.1.2. Doppelbrechung
In einem undeformierten Netzwerk ist die Ausrichtung der Kettensegmente
statistisch. Eine makroskopische Deformation des Netzwerks führt zur teilweisen
Ausrichtung der Kettensegmente, so dass diese nicht mehr isotrop verteilt sind.
Aufgrund der richtungsabhängigen Polarisierbarkeit der Polymerkettensegmente ist
die
makroskopische
richtungsunabhängig.
Polarisierbarkeit
Die
der
Brechungsindizes
Probe
n
dann
in
den
nicht
mehr
verschiedenen
Raumrichtungen sind infolge dessen nicht mehr identisch, es tritt Doppelbrechung
auf. Die Doppelbrechung ∆n ist definiert als die Differenz der Brechungsindizes
parallel ( n ) und senkrecht zur Zugrichtung ( n⊥ ).
∆n = n − n⊥
Nach
einer
theoretischen
Betrachtung
von
(2.10)
Kuhn
und
Grün[22] kann
die
Doppelbrechung unter Annahme einer Gauß-Verteilung des Ketten-End-zu-EndAbstandes, eines affinen Netzwerkmodells sowie des Vorliegens von isolierten,
einzelnen
Ketten
ohne
Wechselwirkungen
untereinander
folgendermaßen
beschrieben werden
2
2
2π ( n + 2 )
∆n = n|| − n⊥ =
O ⋅ (α 1 − α 2 ) ⋅ λ
15
n
(2.11)
Dabei sind n der Brechungsindex des unverstreckten Netzwerks, O die
Orientierungsverteilungsfunktion der Kettensegmente, α1 die Polarisierbarkeit
7
Grundlagen
entlang der Längsachse eines Fadenelementes und α2 die Polarisierbarkeit senkrecht
dazu.
Bei der experimentellen Überprüfung der Theorie von Kuhn und Grün treten in
vielen Fällen Ungenauigkeiten auf, die auf die Annahmen, die zur Herleitung der
Doppelbrechung gemacht wurden, zurückgeführt werden können. Ersetzt man die
Gauß-Verteilung durch eine Langevin-Funktion, berücksichtigt außerdem die
Beweglichkeit der Netzpunkte (Phantom-Netzwerkmodell) sowie Verschlaufungen
(Constrained Chain/Junction-Modell), gelangt man zu einem Ausdruck, der eine gute
Beschreibung für das reale Verhalten der Netzwerke liefert[23-25].
∆nred =
∆nph 
∆nc 
1+

λ  ∆nph 
(2.12)
∆nph ist dabei der Anteil der Doppelbrechung, der seinen Ursprung im PhantomNetzwerkmodell hat. ∆nc beschreibt den Anteil des Constrained Chain/JunctionModell. Der Verlauf der Doppelbrechung ist nicht länger linear von der Dehnung
abhängig.
Die Spannungsdoppelbrechung von Poly(dimethylsiloxan), das dem in dieser Arbeit
verwendete Polymerrückgrat in seiner Struktur sehr ähnlich ist, liegt bei einer
Dehnung von 25 % im Bereich von 6⋅10-5 [26]. Wie später gezeigt wird, kann diese von
der
Polymerkette
ausgehende
Doppelbrechung
im
Vergleich
zu
der
Doppelbrechung, die durch die mesogenen Seitengruppen verursacht wird,
vernachlässigt werden.
2.2. Niedermolekulare Flüssigkristalle
Moleküle mit ausreichender Formanisotropie können zwischen dem festen,
kristallinen Zustand und dem flüssigen, isotropen Zustand eine sogenannte
Mesophase ausbilden. Diese kombiniert den flüssigen Charakter einer Flüssigkeit mit
den anisotropen Eigenschaften des Kristalls. Flüssigkristalle können verschiedene
flüssigkristalline Phasen ausbilden[5].
8
Grundlagen
Bei kalamitischen (stäbchenförmigen) Flüssigkristallen, die in dieser Arbeit
untersucht
werden,
erfolgt
die
Anordnung
der
Stäbchenmoleküle
durch
Dispersionswechselwirkungen untereinander in einer Vorzugsrichtung, die als
Direktor n bezeichnet wird. Es kann zwischen drei Hauptklassen unterschieden
werden. In nematischen Flüssigkristallen sind die Molekülschwerpunkte regellos
angeordnet,
es
existiert
neben
der
ein-
oder
dreidimensionalen
Orientierungsfernordnung keine Positionsfernordnung (Abbildung 2.2 a). In der
smektischen Phase sind die Molekülschwerpunkte in Schichten angeordnet, wobei
die
Moleküle
innerhalb
Orientierungsfernordnung
dreidimensional.
Durch
der
ist
die
wie
Schichten
in
der
Anordnung
in
frei
beweglich
nematischen
Schichten
Phase
ist
der
sind.
Ihre
ein-
oder
Grad
der
Positionsfernordnung höher, es liegt eine eindimensionale Positionsfernordnung vor.
Die smektische Phase kann in mehrere Arten unterteilt werden. Die wichtigsten
Phasen sind die smektisch-A- (Abbildung 2.2 b) und die smektisch-C-Phase
(Abbildung 2.2 c). Während in der smektisch-A-Phase die Direktorrichtung n mit der
Flächennormalen A der Mesogenschichten zusammenfällt, ist in der smektisch-CPhase die Flächennormale der Mesogenschichten in Bezug auf den Direktor verkippt.
Nematische Phasen enthalten oft smektische Cluster. Solche Phasen werden als
cybotaktisch-nematische Phasen bezeichnet.
a)
Abbildung 2.2
b)
c)
Verschiedene niedermolekulare flüssigkristalline Phasen; a) nematische Phase,
b) smektisch-A-Phase, c) smektisch-C-Phase
Eine weitere Art von Flüssigkristallen sind die cholesterischen oder chiral
nematischen Phasen. Sie werden gebildet, wenn alle Mesogene oder ein Teil davon
9
Grundlagen
chirale Zentren besitzen. Man kann sich cholesterische Flüssigkristalle aus
nematischen Schichten mit planarer Orientierung aufgebaut vorstellen. Der Direktor
übereinanderliegender Schichten wird immer um einen konstanten Winkel gedreht.
Eine charakteristische Größe ist die Höhe, die überwunden wird, bis eine Drehung
von 360° erreicht ist. Diese wird pitch genannt und ist entscheidend für die optischen
Eigenschaften der cholesterischen Phase.
2.3. Flüssigkristalline Polymere
Verbindet
man
mesogene
Einheiten
durch
flexible
Molekülgruppen
zu
Makromolekülen, entstehen flüssigkristalline Polymere. Diese haben ähnliche
Eigenschaften wie ihre niedermolekularen Analoga und können je nach Art der
Anbindung der Mesogene an die Polymerkette in verschiedene Typen unterteilt
werden. Die Klassifizierung ist in Abbildung 2.3 gezeigt.
Seitenkettenpolymer
Hauptkettenpolymer
„end-on“
„side-on“
Abbildung 2.3
Klassifizierung von flüssigkristallinen Polymeren
Sind die Mesogene mit Hilfe eines Spacers seitlich an das Polymerrückgrat befestigt,
spricht man von Seitenkettenpolymeren, sind sie Bestandteil des Polymerrückgrats,
werden sie Hauptkettenpolymere genannt. Ein weiteres Unterscheidungskriterium
ist die Lage des Befestigungspunktes der Mesogene. Ist das Mesogen am Ende seiner
Längsachse mit dem Spacer verbunden, spricht man von end-on-Fixierung. Ist es
10
Grundlagen
relativ mittig an seiner Längsseite aufgehängt, handelt es sich um eine side-onFixierung.
In der vorliegenden Arbeit werden Seitenkettenpolymere untersucht, deren
Mesogene end-on mit dem Polymerrückgrat verbunden sind und eine nematische
Phase aufweisen.
2.4. Flüssigkristalline Seitenkettenpolymere
Da flüssigkristalline Seitenkettenpolymere und –elastomere synthetisiert und
untersucht werden sollen, werden diese hier gesondert betrachtet. Hauptaugenmerk
wird dabei auf die lokale und globale Netzkettenkonformation gelegt, sowie auf
Möglichkeiten, diese zu steuern.
2.4.1. odd-even-Effekt
Flüssigkristalline Seitenkettenpolymere kann man sich aus zwei Subsystemen
aufgebaut vorstellen: dem Polymerrückgrat und den mesogenen Seitengruppen. Bei
nicht allzu langen Alkylspacerketten zwischen den beiden Einheiten ist die
Wechselwirkung der beiden Subsysteme sterischer Natur. Da 2H-NMR-Messungen
an Seitenkettenpolymeren mit deuteriertem Alkylspacer einen hohen Ordnungsgrad
der Spacerketten zeigen[27], geht man von einer all-trans-Konfiguration der Ketten
aus. Die Orientierung der Mesogene in Bezug auf die Polymerhauptkette hängt dann
von der Anzahl der Spacer-Atome ab[13-18]. Ist die Anzahl der Alkylspacer-Atome
ungerade
(z.
B.
C3-Spacer),
orientiert
sich
das
Mesogen
senkrecht
zur
Polymerhauptkette. Ist sie gerade (z. B. C4-Spacer) nimmt das Mesogen bevorzugt
eine parallele Lage zum Polymerrückgrat ein. Man spricht vom odd-even-Effekt. Dies
ist in Abbildung 2.4 anhand der hier verwendeten Mesogene gezeigt.
11
Grundlagen
a)
b)
n
Si
Si
Si
Si
Si
Si
Abbildung 2.4
n
Veranschaulichung des odd-even-Effektes; a) ungerade Anzahl von AlkylspacerAtomen (C3), b) gerade Anzahl von Alkylspacer-Atomen (C4)
2.4.2. Knäuelanisotropie
Isotrope Polymere bzw. flüssigkristalline Polymere in der isotropen Phase nehmen
die entropisch begünstigte Konformation eines sphärischen Knäuels ein. In der
flüssigkristallinen Phase findet man ohne äußeren Einfluss eine Abweichung von der
sphärischen Konformation[7-12]. Die Dispersionswechselwirkung zwischen den
Mesogenen, die zu einer Orientierungsfernordnung führt, übt eine Kraft aus, die
dem Bestreben des Polymers, sich in der entropisch günstigeren Weise anzuordnen,
entgegengesetzt ist. Die Richtung der dadurch resultierenden Deformation bezüglich
des Direktors hängt von der lokalen Anordnung von Mesogen und Polymerrückgrat
relativ zueinander gemäß des odd-even-Effekts ab. Dieser Zusammenhang wird durch
die Theorie von Warner et al.[28,
29]
beschrieben und ist in Abbildung 2.5
veranschaulicht. Liegt eine ungerade Anzahl von Alkylspaceratomen vor, nimmt das
Polymerknäuel
eine
im
Bezug
zum
Direktor
abgeflachte
Form
an.
Der
Trägheitsradius parallel zum Direktor ist kleiner als der senkrecht dazu. Man spricht
von einer global oblaten Knäuelkonformation. Bei uniaxialer Deformation richtet sich
das Polymerknäuel mit seiner Längsachse entlang der Zugrichtung aus, die
Mesogene somit senkrecht dazu. Man spricht von einer negativen Kopplung.
12
Grundlagen
lokal oblat
n
lokal prolat
global oblat
global prolat
n
Abbildung 2.5
Lokale und globale Konformation in Seitenkettenpolymeren
Bei geradzahligem Alkylspacer ist das Polymerknäuel gestreckt und der
Trägheitsradius parallel zum Direktor größer als der senkrecht dazu. Es liegt eine
global prolate Konformation des Knäuels vor. Bei einer uniaxialen Deformation
kommt es zu einer parallelen Orientierung sowohl der Polymerhauptkette als auch
der Mesogene relativ zur Zugrichtung. In diesem Fall ist die Kopplung positiv.
2.4.3. Steuerung der Knäuelanisotropie und Nullkopplung
Mitchell et al. untersuchten eine Reihe von nematischen Seitenkettenpolymeren auf
Acrylatbasis bezüglich des Zusammenhangs zwischen der Länge ihres Spacers
zwischen Polymerrückgrat und Mesogen und dem Vorzeichen der Kopplung der
flüssigkristallinen Phase an das Polymernetzwerk[18]. Das Resultat war ein streng
alternierendes Vorzeichen der Kopplung mit regelmäßiger Variation der Spacerkette
um jeweils ein Atom. Basierend auf dem gleichen Polymersystem zeigten Guo et al.,
dass durch gleichzeitige Anbindung von Mesogenen mit unterschiedlicher lokaler
Netzkettenkonformation an das Polymerrückgrat die Knäuelanisotropie gesteuert
13
Grundlagen
werden kann[19]. Die Monomere des untersuchten Systems sind in Abbildung 2.6
gezeigt. Mesogen I und II unterscheiden sich lediglich in der Anzahl der C-Atome in
der Spacerkette. Der Einbau von Molekül III in die Polymerkette dient dazu, die
Polymere später zu vernetzen.
Die Polymere und Elastomere wurden mit Hilfe von Röntgenstreuung untersucht.
Aus den Diffraktogrammen wurde der Ordnungsgrad bestimmt (s. Abschnitt 2.6.1).
O
O
O
O
O
CN
Mesogen I
O
O
O
O
O
CN
Mesogen II
O
O
OH
III
Abbildung 2.6
Von Guo et al. untersuchtes System zur Reduktion der Knäuelanisotropie
Homopolymere, die ausschließlich aus Mesogen I bestehen, zeigen bei uniaxialer
Deformation eine Ausrichtung des Direktors senkrecht zur Zugrichtung, während
Homopolymere aus Mesogen II eine Ausrichtung des Direktors parallel zur
Zugrichtung zeigen. Bei gleichzeitiger Einbindung der beiden Mesogene in ein
Polymer erhält man ein Orientierungsverhalten, das vom Konzentrationsverhältnis
der Mesogene abhängt. Wird ausgehend vom Homopolymer mit Mesogen I der
Anteil an Mesogen II erhöht, nimmt in den uniaxial deformierten Proben der
parallel zur Zugrichtung bestimmte Ordnungsparameter zunächst leicht, dann
sprunghaft ab. Bei einer Konzentration von Mesogen II von ca. 72 mol-% ist der
Ordnungsparameter praktisch null. Bei weiterer Erhöhung des Anteils an Mesogen
II wird der Ordnungsparameter negativ. Die Tatsache, dass die Nullkopplung nicht
14
Grundlagen
bei einem Verhältnis der Mesogene von 50:50 auftritt, zeigt die unterschiedliche
Stärke der Kopplung abhängig von der Länge des Spacers. Der kürzere Spacer in
Mesogen I führt zu einer viel stärkeren Kopplung der Mesogene an das
Polymerrückgrat als der um eine C-Einheit längere Spacer in Mesogen II.
Auch in den entsprechenden Coelastomeren kann der Effekt der Kopplungsvariation
beobachtet werden, wobei die Größe des Ordnungsparameters im Vergleich zu den
unvernetzten
Polymeren
unverändert
ist.
Allerdings
verschiebt
sich
die
Konzentration, bei der die Nullkopplung auftritt, auf einen Anteil von 81 mol-%
Monomer
II.
Der Verlauf der Ordnungsparameterkurve für verschiedene
Coelastomere ist in Abbildung 2.7 gezeigt.
1,0
Maximaler Ordnungsgrad
0,8
n
0,6
0,4
0,2
0,0
-0,2
n
-0,4
0
20
40
60
80
100
mol % II
Abbildung 2.7
Ornungsgrad parallel zur Zugrichtung bei Coelastomeren verschiedener
Zusammensetzung
2.5. Flüssigkristalline Elastomere
Durch einen weiteren Fixierungsschritt erhält man aus flüssigkristallinen Polymeren
flüssigkristalline Elastomere. Es gibt verschiedene Synthesemethoden, durch die
solche Netzwerke hergestellt werden können. Der konventionelle Weg zur
Herstellung
von
Seitenkettenelastomeren
auf
Polysiloxanbasis
ist
eine
Eintopfreaktion, in der ein Präpolymer in einer polymeranalogen Reaktion mit dem
15
Grundlagen
Mesogen und einem Vernetzer direkt zum Netzwerk umgesetzt wird[30]. Eine andere,
in dieser Arbeit verwendete Variante liefert das Elastomer in zwei Schritten[31].
Zunächst wird ein lineares Polymer hergestellt, indem Präpolymer, Mesogen und ein
Photovernetzer zusammen in einer polymeranalogen Reaktion umgesetzt werden.
Da der Vernetzer durch Licht im ultravioletten Bereich aktiviert wird, und die
Reaktion unter Lichtausschluß durchgeführt wird, reagiert dabei der Vernetzer nicht.
Erst in einem zweiten, separaten Schritt erfolgt die gezielte Bestrahlung mit UVLicht, was zu einer Aktivierung des Vernetzers und so zu einer Vernetzungsreaktion
führt.
Erfolgt die Synthese des Netzwerks ohne die Einwirkung eines externen
mechanischen, elektrischen oder magnetischen Feldes, wird eine sogenannte
Polydomäne erhalten. Innerhalb der Probe sind die Mesogene in kleinen Domänen
gleich ausgerichtet, die Direktoren der einzelnen Domänen sind aber statistisch
verteilt. Makroskopisch ist die Probe nicht orientiert. Da die Größe der Domänen im
Bereich der Wellenlänge von sichtbarem Licht liegt, wird das Licht gestreut und die
Probe erscheint trüb.
Wird das Elastomer in Gegenwart eines externen Feldes synthetisiert, liegen die
Direktoren der Domänen nicht mehr statistisch verteilt vor, es erfolgt eine
einheitliche Ausrichtung durch die ausgeübte Kraft. Man bezeichnet eine einheitlich
orientierte Probe als Monodomäne. Es wird hierfür auch der Begriff liquid single
crystal elastomer (LSCE) verwendet, auch wenn dies ein idealisierter Begriff ist, da ein
perfekter Einkristall nie erreicht wird.
Eine Monodomäne wird bei der zuerst beschriebenen Eintopfsynthese dadurch
erhalten, dass die Elastomere, sobald sie schwach vernetzt sind, aus der zur Synthese
verwendeten Zentrifugenform genommen werden, und ein mechanisches Feld
angelegt wird. Unter der Krafteinwirkung lässt man das Netzwerk nachvernetzen,
bis die Reaktion vollständig ist[32].
Bei der Herstellung der Elastomere in zwei Schritten erfolgt die Orientierung des im
ersten Schritt erhaltenen linearen Polymers in einem magnetischen oder elektrischen
16
Grundlagen
Feld. Aufgrund der hohen Viskosität der Polymere muss die Orientierung bei
erhöhter Temperatur knapp unterhalb des Klärpunkts durchgeführt werden. Die
Fixierung dieser Orientierung erfolgt durch Bestrahlung mit UV-Licht[31].
2.6. Eigenschaften flüssigkristalliner Elastomere
In diesem Abschnitt wird auf die doppelbrechende Eigenschaft flüssigkristalliner
Elastomere und die Möglichkeit eingegangen, daraus den temperaturabhängigen
Ordnungsgrad einer Probe zu bestimmen. Außerdem wird die Landau-de GennesTheorie behandelt, die die Phasenumwandlung von der nematischen in die isotrope
Phase beschreibt.
2.6.1. Ordnungsgrad
Die Orientierung der Mesogene in einem nematischen Flüssigkristall kann durch den
Ordnungsgrad S[33-35] charakterisiert werden, der als das zweite Legendre-Polynom
der Orientierungsverteilungsfunktion der Mesogenlängsachsen in Bezug auf den
Direktor definiert ist.
S = P2 ( cos θ ) =
1
3 ⋅ cos 2 θ − 1
2
(2.13)
Dabei stellt θ den Winkel zwischen einer Bezugsrichtung (üblicherweise dem
Direktor n) und der Moleküllängsachse eines betrachteten Mesogens dar (Abbildung
2.8). Die statistische Mittelung über alle θ-Werte erfolgt, um die zeitlichen
Fluktuationen
der
Orientierung
aufgrund
von
thermischer
Bewegung
zu
berücksichtigen.
Man kann drei theoretische Grenzfälle betrachten. Sind alle Mesogene einheitlich
ausgerichtet, d. h. θ nimmt einen Wert von 0° an, ist die Probe perfekt geordnet, und
der Ordnungsgrad ist S=1. Ist die Probe völlig ungeordnet, wie es in der isotropen
Phase der Fall ist, nimmt der Winkel einen Mittelwert von 54,7° zur betrachteten
Richtung ein. Daraus errechnet sich ein Ordnungsgrad von S=0. Der Ordnungsgrad
17
Grundlagen
einer Probe kann auch negative Werte annehmen. Ein Grenzfall stellt die senkrechte
Ausrichtung der Mesogene zur Bezugsrichtung dar. Der Winkel θ hat also einen
Wert von 90°, und der Ordnungsgrad ist gemäß Gleichung (2.13) S=-0,5.
Θ
n
Abbildung 2.8 Graphische Erläuterung zur Definition des Ordnungsgrades
Die Bestimmung des Ordnungsgrades wird häufig mit Hilfe von Röntgenstreuung
durchgeführt. Durch den regelmäßigen Lateralabstand der Mesogene kommt es zu
konzentrischen Reflexen im Weitwinkelbereich, die in der Richtung senkrecht zum
Direktor Maxima aufweisen. Je geordneter die Probe ist, desto schmaler sind diese
Maxima. Aus der azimuthalen Intensitätsverteilung kann der Ordnungsgrad
berechnet werden[36,
Ordnungsgrad
. Dabei kann allerdings nicht zwischen dem nematischen
37]
innerhalb
der
mesoskopischen
Domänen
SN
und
dem
makroskopischen Ordnungsgrad der Direktoren der einzelnen Domänen SD
unterschieden werden. Es kann nur das Produkt S=SN⋅SD bestimmt werden.
Röntgenstreuung zur Ordnungsgradbestimmung kann angewandt werden, wenn
die Proben eine gewisse Dicke haben und so deutliche Reflexe auftreten. Die hier
untersuchten Elastomere haben lediglich eine Dicke von ca. 20 µm, was auch bei
langer Bestrahlungszeit zu nicht auswertbaren Streuintensitäten führt.
18
Grundlagen
2.6.2. Doppelbrechung
Die Bestimmung des Ordnungsgrades kann neben der Röntgenstreuung auch mit
Hilfe von Doppelbrechungsmessungen durchgeführt werden[38].
Die Doppelbrechung ∆n ist definiert als
∆n = ne − no
(2.14)
Dabei ist ne der Brechungsindex des außerordentlichen Strahls und no der
Brechungsindex des ordentlichen Strahls. Nimmt ∆n Werte größer als null an, spricht
man von einer optisch positiven Substanz. Ist ∆n negativ, nennt man sie optisch
negativ.
Die Doppelbrechung eines Flüssigkristalls ist abhängig von der Temperatur. Mit
steigender Temperatur nimmt sie ab und verschwindet sprunghaft bei der
Phasenumwandlungstemperatur. Der Verlauf der beiden Brechungsindizes ist
beispielhaft für einen optisch positiven uniaxialen Flüssigkristall in Abbildung 2.9
skizziert. Der Brechungsindex der isotropen Phase wird als ni bezeichnet.
Die Doppelbrechung in flüssigkristallinen Polymeren oder Elastomeren ist
hauptsächlich auf die Anisotropie der Brechungsindizes der mesogenen Einheiten
zurückzuführen. Der Beitrag, der durch die Ausrichtung von Kettensegmenten des
Polymerrückgrats auftritt, ist wesentlich kleiner. Während die Doppelbrechung bei
einer Dehnung von Poly(dimethylsiloxan) um 25 % im Größenordnungsbereich von
6⋅10-5 liegt[26], tritt bei den in dieser Arbeit untersuchten flüssigkristallinen
Elastomeren, die ebenfalls auf einem Polysiloxan als Polymerrückgrat basieren, je
nach Probendicke eine Doppelbrechung zwischen 0,10 und 0,12 auf. Die von der
Polymerkette
ausgehende
Doppelbrechung
kann
also
gegenüber
der
Doppelbrechung der flüssigkristallinen Phase vernachlässigt werden.
19
Grundlagen
Brechungsindex n
ne
ni
no
Temperatur T
Abbildung 2.9
Schematischer Verlauf des außerordentlichen (ne) und des ordentlichen
Brechungsindexes (no) in Abhängigkeit der Temperatur am Beispiel eines
optisch positiven uniaxialen Flüssigkristalls
Die Anisotropie der Brechungsindizes parallel und senkrecht zur optischen Achse
der
flüssigkristallinen
Phase
kommt
durch
die
anisotropen
molekularen
Polarisierbarkeiten in den Mesogenen parallel und senkrecht zur Moleküllängsachse
zustande.
Eine
allgemeine
Verknüpfung
zwischen
molekularer
Polarisierbarkeit
und
Brechungsindex in einer isotropen Flüssigkeit wird durch die Lorenz-LorentzGleichung hergestellt.
n2 − 1 4
= π ⋅ N ⋅α
n2 + 2 3
(2.15)
Ν ist die Anzahldichte der Moleküle und α die mittlere Polarisierbarkeit der
Flüssigkeit. In dieser Gleichung ist berücksichtigt, dass das auf die Moleküle
wirkende Feld Eloc in der kondensierten Phase vom angelegten externen Feld E
abweicht, was für Flüssigkeiten oft durch Verwendung des Lorentz-Felds
berücksichtigt wird.
Eloc =
20
n2 + 2
⋅E
3
(2.16)
Grundlagen
Bei Flüssigkristallen sind die Polarisierbarkeiten parallel und senkrecht zur optischen
Achse unterschiedlich. Sie sind verknüpft mit dem Ordnungsgrad S und den
molekularen Polarisierbarkeiten.
2
3
(2.17)
1
3
(2.18)
α e = α + ∆α ⋅ S
α o = α − ∆α ⋅ S
Dabei ist α die mittlere molekulare Polarisierbarkeit
α=
1
(α + 2α ⊥ )
3
(2.19)
und ∆α die molekulare Polarisierbarkeitsanisotropie
∆α = α − α ⊥
(2.20)
α ist die molekulare Polarisierbarkeit parallel zur Längsachse des Mesogens, α ⊥ die
senkrecht zur Längsachse.
Die beiden Gleichungen (2.17) und (2.18) können als Definition des Ordnungsgrades
angesehen
werden[39,40]
und
sind
kompatibel
mit
der
Formulierung
des
Ordnungsgrades nach Gleichung (2.13), wenn die molekularen Polarisierbarkeiten
für den betrachteten Temperaturbereich als unabhängig von der Umgebung
angesehen werden können.
Will
man
die
Temperaturabhängigkeit
des
Ordnungsgrades
und
die
Polarisierbarkeiten bestimmen, muss man das lokale Polarisationsfeld in einem
anisotropen Medium berücksichtigen. Es muss ein passendes Modell gefunden
werden.
Das unkomplizierteste Modell basiert darauf, die Lorentz-Lorenz-Beziehung (2.15)
auf jede Richtung bezüglich der optischen Achse einzeln anzuwenden.
nj 2 − 1
4
= π ⋅ N ⋅α j
nj + 2 3
2
(2.21)
Der Index j steht entweder für außerordentlich e oder ordentlich o. Allerdings erweist
sich diese Beziehung sowohl theoretisch als auch experimentell als unpassend[41].
21
Grundlagen
Für qualitative Interpretationen der experimentellen Ergebnisse scheint es passend,
die von Vuks[42] empirisch für Kristalle entwickelten Gleichungen zu verwenden[43].
Sie werden häufig in optischen Studien an Flüssigkristallen (vor allem an
nematischen Systemen) angewandt, obwohl das lokale Feld in dieser Näherung
isotrop ist.
ne 2 − 1 4
= π ⋅ N ⋅α e
n2 + 2 3
(2.22)
no 2 − 1 4
= π ⋅ N ⋅α o
n2 + 2 3
(2.23)
Der Unterschied zu der Methode, die Lorentz-Lorenz-Gleichung auf die beiden
optischen Achsen getrennt anzuwenden (2.21), ist der Gebrauch des mittleren
Brechungsindex n statt des richtungsabhängigen Brechungsindexes im Nenner.
Der mittlere Brechunsindex ist gegeben durch
n2 =
1 2
ne + 2n02 )
(
3
(2.24)
Der größte Vorteil des Modells von Vuks ist, dass experimentelle Daten ohne die
Einführung zusätzlicher Parameter mit innerer Konsistenz beschrieben werden
können.
Kombination der Gleichungen (2.17) und (2.18) mit Gleichung (2.24) ergibt
n2 − 1 4
= π ⋅ N ⋅α
n2 + 2 3
(2.25)
ne 2 − no2 4
= π ⋅ N ⋅ S ⋅ ∆α
n2 + 2
3
(2.26)
und
Die bewiesene Konsistenz der Daten impliziert, dass sich die Anisotropie des inneren
Feldes bei der Umwandlung von der nematischen in die isotrope Phase nicht ändert.
Diese Annahme ist plausibel, da das innere Feld von den nächsten Nachbarn eines
Moleküls aufgebaut wird und die Nahordnung in der flüssigen Phase auch oberhalb
der Umwandlungstemperatur weiterbesteht.
22
Grundlagen
Die
Temperaturabhängigkeit
des
Ordnungsgrades
multipliziert
mit
der
Polarisierbarkeitsanisotropie kann aus refraktometrischen Daten mit Hilfe von
Gleichung (2.26) erhalten werden.
2.6.3. Bestimmung des Ordnungsgrades aus der Doppelbrechung
Gleichung (2.26) ist ein Ausdruck, mit dessen Hilfe man den Verlauf des
Ordnungsgrads mit der Temperatur bestimmen kann. Um absolute Werte des
Ordnungsgrades zu erhalten sind weitere Annahmen notwendig.
Sind für eine flüssigkristalline Substanz Brechungsindizes und Strukturdaten des
entsprechenden Kristalls verfügbar, kann die Polarisierbarkeitsanisotropie des
Kristalls auch für die nematische Phase verwendet werden. Dabei wird die Annahme
gemacht, dass innere Feldeffekte bei der Umwandlung von der kristallinen Phase in
die
nematische
analog
zur
nematisch-isotropen
Phasenumwandlung
vernachlässigbar sind.
Alternativ kann eine Extrapolationsmethode angewandt werden. Haller beobachtete,
dass im Bereich tiefer Temperaturen der Logarithmus des Ordnungsgrades
multipliziert mit der Polarisierbarkeitsanisotropie proportional zum Logarithmus
der negativen reduzierten Temperatur τ ist[44].
log ( S ⋅ ∆α ) ∼ log ( −τ )
(2.27)
Dabei ist
τ=
T − Tn ,i
Tn ,i
(2.28)
Unter der Annahme, dass der lineare Zusammenhang in Gleichung (2.27) auch in
einer hypothetischen unterkühlten nematischen Phase bis zu einer Temperatur von 0
K, bei der der Ordnungsgrad 1 beträgt, bestehen bleibt, erhält man durch
Extrapolation der experimentellen Daten auf τ =-1 die Polarisierbarkeitsanisotropie
∆α.
23
Grundlagen
Stehen keine Dichtedaten zur Verfügung, mit deren Hilfe zusammen mit dem aus
obiger Extrapolation ermittelten Wert für ∆α der Ordnungsgrad nach Gleichung
(2.26) berechnet werden kann, kann der Quotient aus den Gleichungen (2.26) und
(2.25) zur Extrapolation herangezogen werden.
 ne2 − no2 
S ⋅ ∆α 
log 
=
log

 2
 = C + A ⋅ log τ
 α 
 n −1 
(2.29)
Extrapolation auf τ =-1 liefert das Verhältnis ∆α / α .
Bei der Auftragung gemäß Gleichung (2.29) kann bei höheren Temperaturen eine
leichte Krümmung in der Geraden auftreten. Diese lässt sich beseitigen, indem man
die reduzierte Temperatur statt auf die Phasenumwandlungstemperatur Tn,i auf eine
Temperatur T* bezieht, bei der der Ordnungsgrad null wäre, wenn der
kontinuierliche
Abfall
nicht
durch
die
Diskontinuität
aufgrund
der
Phasenumwandlung erster Ordnung gestoppt würde. Dies ist äquivalent zu der
Aussage, dass die experimentell ermittelten Brechungsindizes mit folgender
dreiparametrigen Formel gefittet werden können[45].
 n2 − n2 
log  e 2 0  = C + A ⋅ log ( 1 − B ⋅ T )
 n −1 
(2.30)
Formel (2.30) ist anwendbar auf den kompletten Temperaturbereich.
Den Messungen in dieser Arbeit wird Gleichung (2.29) zugrundegelegt. Die
reduzierte Temperatur wird auf die Phasenumwandlungstemperatur Tn,i bezogen
und Temperaturen nahe der Phasenumwandlungstemperatur vernachlässigt.
Aus dem refraktometrischen Messprinzip werden die Brechungsindizes nicht separat
erhalten, sondern die Doppelbrechung direkt bestimmt. Es ist daher notwendig, die
Gleichung (2.29) umzuformen.
Die Differenz der Quadrate des außerordentlichen und des ordentlichen
Brechungsindexes ist proportional zur Doppelbrechung ∆n.
ne2 − n02 = n ⋅ ∆n
(2.31)
Setzt man (2.31) in (2.29) ein, kann der konstante Teil aus dem Logarithmus der
linken Seite mit in die Konstante auf der rechten Seite einbezogen werden.
24
Grundlagen
log ( ∆n ) = C '+ A ⋅ log τ
(2.32)
Extrapolation auf eine Temperatur von 0 K liefert die Doppelbrechung am absoluten
Nullpunkt zu
∆n0 = exp ( C ' )
(2.33)
Bildet man den Quotienten aus Gleichung (2.26) bei einer beliebigen Temperatur und
der Temperatur am absoluten Nullpunkt und setzt Gleichung (2.31) ein, erhält man
∆n(T ) S(T )
=
∆n0
S0
(2.34)
Der Ordnungsgrad am absoluten Nullpunkt wird als perfekt angenommen und hat
somit einen Wert von S0=1. Ist die Doppelbrechung einer Probe in Abhängigkeit der
Temperatur bekannt, lässt sich durch die umgeformte Gleichung (2.34) in
Kombination mit Gleichung (2.33) der Ordnungsgrad in Abhängigkeit der
Temperatur bestimmen.
S(T ) =
∆n
exp ( C ' )
(2.35)
2.6.4. Landau-de Gennes Theorie
2.6.4.1 Freie Energie eines nematischen Systems
Bereits 1975 schlug de Gennes vor, nematische Polymere könnten in Netzwerke mit
außergewöhnlichen
Eigenschaften
Charakteristika
nannte
er
überführt
werden
.
[46]
Als
mögliche
nicht-lineares oder diskontinuierliches Spannungs-
Dehnungs-Verhalten, spontane Dimensionsänderung und Kopplung zwischen
mechanischen, optischen und elektrischen Feldern.
Die von de Gennes vorgeschlagene rein phänomenologische Theorie war sehr
allgemein auf alle Typen von nematischen Polymeren bezogen und basierte auf
starken und einfachen Symmetrieargumenten unabhängig von mikroskopischen
Modellen.
25
Grundlagen
Die Basis der Arbeiten von de Gennes bildete die Landau-Theorie[6], die
Phasenumwandlungen zweiter Ordnung beschreibt. Dabei wird die Freie Energie F
eines Systems in einer Reihe nach einem Ordnungsparameter S entwickelt. De
Gennes modifizierte die Theorie dahingehend, dass sie auch auf die nematischisotrope Phasenumwandlung, die schwach erster Ordnung ist, angewandt werden
kann[39, 40].
Die Freie Energie F eines nematischen Systems ohne Einwirkung eines äußeren
Feldes kann nach
F ( S , p , T ) = F0 ( p , T )S =0 +
1
1
1
A (T ) ⋅ S2 + B ⋅ S 3 + C ⋅ S 4 + ⋅⋅⋅
2
3
4
(2.36)
beschrieben werden, wobei p der Druck, T die Temperatur, F0 die Freie Energie der
isotropen Phase sind. B und C sind in guter Näherung temperaturunabhängige
Konstanten sind. Der Parameter A ist temperaturabhängig und gegeben durch
A = A0 ⋅ (T − T * )
Der
Koeffizient
A
ändert
sein
Vorzeichen
(2.37)
bei
der
hypothetischen
Phasenumwandlungstemperatur T*. Dies ist die Temperatur, bis zu der die isotrope
Phase maximal unterkühlt werden kann. A0 ist nur schwach temperaturabhängig
und kann in der Umgebung der Phasenumwandlung als konstante Größe angesehen
werden.
Aus der Reihenentwicklung (2.36) resultiert ein Verlauf der Freien Energie in
Abhängigkeit des Ordnungsgrades für verschiedene Temperaturbereiche, wie er in
Abbildung 2.10 dargestellt ist.
26
Grundlagen
0.01
*
Freie Energie F
3
Freie Energie F [J/cm ]
T>>T
T=T
0.00
+
T=T n,i>T
*
T=T
*
T n,i = 57.8°C
T<T
*
*
T = 56.6°C
-0.01
-0.4
-0.2
0.0
0.2
0.4
0.6
0.8
1.0
Ordnungsgrad
Ordnungsgrad S S
Abbildung 2.10
Freie Energie in Abhängigkeit vom Ordnungsgrad für verschiedene
Temperaturen
Es existieren drei charakteristische Temperaturen T+, Tn,i und T*. Liegt die
Temperatur oberhalb von T+, befindet sich die Probe in der isotropen Phase. Der
Verlauf der Freien Energie weist ein Minimum bei einem Ordnungsgrad S=0 auf.
Entspricht die Temperatur exakt T+, besteht neben einem lokalen Minimum bei S=0
ein Sattelpunkt bei einem Ordnungsgrad von S>0. Bei Temperaturen zwischen T+
und Tn,i tritt zusätzlich zum Minimum bei S=0 ein weiteres lokales Minimum bei S>0
auf, das den Bereich der überhitzten, metastabilen nematischen Phase charakterisiert.
Das Minimum wird mit abnehmender Temperatur zu kleineren Werten der Freien
Energie verschoben, bis es bei T=Tn,i energiegleich mit dem Minimum bei S=0 ist. Das
bedeutet, die isotrope und die nematische Phase koexistieren. Erniedrigt man die
Temperatur weiter, beobachtet man in einem Bereich zwischen Tn,i und T* ein
Minimum bei einem Ordnungsgrad von S>0 und ein lokales Minimum bei S=0.
Dieser Bereich entspricht der unterkühlten, metastabilen isotropen Phase. Das
Minimum geht in einen Sattelpunkt über, wenn die Temperatur T* erreicht ist. Bei
27
Grundlagen
Temperaturen T<T* weist der Verlauf der Freien Energie zwei Minima auf, von
denen das eine bei Ordnungsgraden von S<0 und das andere bei Ordnungsgraden
von S>0 liegt.
2.6.4.2 Freie Energie eines nematischen Netzwerks
Die Formulierung der Freien Energie F in Gleichung (2.36) muss um einige Terme
erweitert werden, um sie auf Netzwerke nematischer Flüssigkristalle anwenden zu
können. Diese Terme beschreiben die elastischen Eigenschaften und die Kopplung
der flüssigkristallinen Phase an das Polymernetzwerk. Zusätzlich wird ein Term
eingeführt, der die Änderung der Freien Energie bei Anlegen eines äußeren
mechanischen Feldes berücksichtigt. Die modifizierte Form der Freien Energie ist
gegeben durch
1
1
1
A (T ) ⋅ S2 + B ⋅ S 3 + C ⋅ S 4 + ⋅⋅⋅
2
3
4
1
+U ⋅ S ⋅ e + ⋅ E ⋅ e 2 − σ ⋅ e
2
F ( S , p , T ) = F0 ( p , T )S =0 +
(2.38)
F0 ist wie in (2.36) die Freie Energie der isotropen Phase, U die Kopplungskonstante,
e=L/L0 die relative Längenänderung, E der elastische Modul des Netzwerks und σ die
angelegte mechanische Spannung.
Der erste zusätzliche Term beschreibt den Anteil der Freien Energie, der durch die
Bindung der Mesogene an das Netzwerk auftritt. Eine charakteristische Größe ist die
Kopplungskonstante U. Diese hängt von der Anbindung der Mesogene an die
Polymerhauptkette ab, d. h. von der Länge und der Natur des Spacers, der das
Mesogen mit dem Rückgrat verbindet. Weiterhin wird von de Gennes angenommen,
dass sie proportional zur Vernetzungsdichte ist[5]. Der zweite zusätzliche Term
entspricht der elastischen Energie des Netzwerks. Der dritte geht aus der
Energieänderung bei Anlegen eines externen mechanischen Feldes hervor.
28
Grundlagen
Betrachtet man die Probe in Abwesenheit eines externen Feldes, kann eine spontane
Verformung eintreten, bis ein Zustand minimaler Freier Energie erreicht ist
( ∂F / ∂e =0). Die Dehnung lässt sich berechnen zu
em =
U ⋅S
E
(2.39)
Durch Einsetzen dieser Gleichgewichtslänge in Formel (2.38) erhält man die Landaude Gennes-Entwicklung der Freien Energie ohne externes Feld in der Form
1
1
1
U 2 ⋅ S2
2
3
4
F ( S , p , T ) = F0 ( p , T )S =0 + A(T ) ⋅ S + B ⋅ S + C ⋅ S + ⋅⋅⋅ −
2
3
4
2⋅E
(2.40)
Der Term, der den Faktor –U2/2E beinhaltet, ist wie der Term mit dem Faktor A(T)
proportional zu S2. Er ist eine Ergänzung zu A(T) und stellt somit eine Verschiebung
von T* in Richtung von Tn,i dar.
In Gegenwart eines externen Feldes gibt die Minimierung der Freien Energie einen
Gleichgewichtswert der Dehnung von
em =
σ + U ⋅S
(2.41)
E
an, der unter Vernachlässigung der Terme mit σ2 zu folgender Formulierung der
Freien Energie führt
F (S ) =
Der
erste
1
1
1
U 2 ⋅ S2 σ ⋅U ⋅ S
A ⋅ S2 + B ⋅ S 3 + C ⋅ S4 + ⋅⋅⋅ −
−
2
3
4
2⋅E
E
Zusatzterm
repräsentiert
wieder
eine
Verschiebung
(2.42)
in
der
Übergangstemperatur, der zweite entspricht exakt einem konventionellen Nematen,
an den ein externes magnetisches oder elektrisches Feld angelegt wird (mit E2 oder
B2=σ).
Durch Minimierung der Freien Energie F, wie sie in Gleichung (2.42) formuliert ist,
nach der Spannung σ wird ein Ausdruck für die Kopplungskonstante U erhalten,
durch den deren Berechnung aus der Auftragung der relativen Länge λ gegen den
Ordnungsgrad S möglich ist. Die relative Länge e wird meist durch die Dehnung
λ=1+e ersetzt.
∂e
∂λ
U = E ⋅   = E ⋅  
 ∂S 
 ∂S 
(2.43)
29
Grundlagen
2.6.4.3 Kritische Größen
Die der Landau-de Gennes Theorie zugrunde liegende Idee ist, dass bei Anlegen
eines schwachen externen Feldes an eine isotrope Phase eine schwache nematische
Ordnung erzeugt wird. Dieser Zustand wird als paranematische Phase bezeichnet.
Der Übergang von der paranematischen in die nematische Phase weist bei nicht allzu
großen Feldern den üblichen Sprung auf, der mit zunehmender Feldstärke kleiner
wird. Außerdem ist der Phasenübergang zu höheren Temperaturen verschoben.
Übersteigt das angelegte Feld eine bestimmte kritische Stärke, wird der Übergang
von der isotropen in die nematische Phase kontinuierlich.
Experimentell wurde an nematischen Elastomeren eine spannungsinduzierte
Doppelbrechung oberhalb der Phasenumwandlungstemperatur[15,
47, 48]
und eine
S
Verschiebung der Phasenumwandlungstemperatur[47, 49] nachgewiesen.
S
σ>σcp
Scp
σcp
Tn,i
Abbildung 2.11
Tcp
T
Verlauf des Ordnungsgrades S mit der Temperatur für verschieden große
angelegte externe Felder
Eine Beschreibung des Verlaufs des Ordnungsgrades mit der Temperatur abhängig
vom angelegten Feldes, wie in Abbildung 2.11 gezeigt, erhält man durch
Minimierung der Freien Energie F nach dem Ordnungsgrad S.
∂F
B 2  A U2 
σ ⋅U
3
= S + ⋅S +  −
=0
 ⋅S −
∂S
C
E ⋅C
 C E ⋅C 
30
(2.44)
Grundlagen
Die kritischen Parameter Scp, Tcp und σcp können durch die höheren Ableitungen der
Freien Energie erhalten werden[50].
∂F ∂ 2 F ∂ 3 F
=
=
=0
∂S ∂S 2 ∂S3
(2.45)
Sie ergeben sich zu
Scp = −
Tcp − Tn0,i = −
B
3C
(2.46)
B2
9 ⋅ a0 ⋅ C
(2.47)
B3 ⋅ E
σ cp = −
27 ⋅ C 2 ⋅ U
(2.48)
2.6.4.4 finite-size-Effekt
Ein ähnliches Verhalten wie das, das durch Anlegen eines externen Feldes
hervorgerufen wird, kann auch durch die Vernetzung der Probe selbst verursacht
werden. Die Vernetzungsstellen führen lokal zu einer reduzierten Mobilität und
beeinflussen
so
die
Orientierung
und
Dynamik
der
Mesogene
in
ihrer
Nachbarschaft[51], sie wirken wie interne Grenzflächen. Der Einfluss ordnender
Grenzflächen auf die nematisch-isotrope Phasenumwandlung in niedermolekularen
Flüssigkristallen wurde von Sheng beschrieben
. Dieses Phänomen wird als
[52, 53]
finite-size-Effekt bezeichnet. Das Unterschreiten einer kritischen Probendicke führt zu
einer
kontinuierlichen
Phasenumwandlung
von
der
nematischen
in
die
paranematische Phase. Der Ordnungsgrad in Abhängigkeit der Temperatur verhält
sich dabei ähnlich wie in der Landau-de Gennes Theorie oberhalb des kritischen
Punktes.
31
Grundlagen
2.7. Dielektrische Eigenschaften von Flüssigkristallen[54]
Die statische, dielektrische Permittivität ε einer isotropen, nicht assoziierten
Flüssigkeit kann näherungsweise durch die Onsager-Gleichung ausgedrückt werden.

ε 0 ( ε − 1) = N ⋅ F ⋅ h ⋅  α +


⋅F
3 kT 
µ2
(2.49)
Darin ist α die molekulare Polarisierbarkeit, µ das Dipolmoment des Moleküls, N die
Anzahl der Moleküle pro Einheitsvolumen, k die Boltzmann-Konstante und T die
Temperatur. Der Feldfaktor F und der Kavitätsfaktor h sind Parameter der Onsager
Theorie.
In Flüssigkristallen sind die dielektrischen Eigenschaften anisotrop. Die Anisotropie
der Dielektrizitätskonstanten ist von großem Interesse, da die meisten praktisch
relevanten elektrooptischen Effekte auf dielektrischer Anisotropie basieren.
In uniaxialen Flüssigkristallen wie nematischen Phasen ist die dielektrische
Anisotropie definiert als
∆ε = ε − ε ⊥
(2.50)
wobei ε die Dielektrizitätskonstante parallel, ε ⊥ die Dielektrizitätskonstante
senkrecht zum Direktor ist.
Größe und Vorzeichen der dielektrischen Anisotropie werden von der molekularen
Struktur des Flüssigkristalls bestimmt. Eine allgemeine theoretische Interpretation
der dielektrischen Anisotropie als Funktion der molekularen Parameter ist durch die
Maier-Meier-Theorie möglich, die eine Erweiterung zur Onsager-Theorie zur
Anwendung auf Flüssigkristalle darstellt. Diese Theorie geht zur Vereinfachung von
einer sphärischen Molekülgeometrie aus, die Polarisierbarkeit ist allerdings
anisotrop. Der Punktdipol µ in der Mitte des Moleküls schließt mit der
Moleküllängsachse einen Winkel β ein. Es wird angenommen, dass ∆ε sehr viel
kleiner als die mittlere dielektische Permittivität ε ist.
ε =
32
ε + 2 ⋅ ε ⊥
3
(2.51)
Grundlagen
Dies bedeutet, dass die Umgebung des Moleküls als kontinuierlich angenommen
wird.
Des weiteren wird angenommen, dass die nematische Phase vom angelegten
elektrischen Feld nicht beeinflusst wird. Basierend auf diesen Näherungen wurden
folgende Gleichungen für die dielektrischen Permittivitäten ε und ε ⊥ eines
nematischen Einkristalls erhalten.


F ⋅µ2
1 − ( 1 − 3 cos 2 β ) ⋅ S  


3 kT

(2.52)

1
F ⋅µ2
1 − ( 1 − 3 cos 2 β ) ⋅ S  
∆α ⋅ S +


3
3 kT

(2.53)
2
3
(ε − 1) ε 0 = N ⋅ F ⋅ h α + ∆α ⋅ S +


(ε ⊥ − 1) ε 0 = N ⋅ F ⋅ h α −

Die dielektrische Anisotropie ist gegeben zu
(ε


F ⋅µ2
−
ε
ε
=
N
⋅
F
⋅
h
⋅
S
∆
α
−
1 − 3 cos 2 β ) 
)
(
⊥
0

2 kT


(2.54)
Darin ist α die mittlere Polarisierbarkeit und ∆α die Anisotropie der molekularen
Polarisierbarkeiten. Die beiden Größen sind durch die Gleichungen (2.19) bzw. (2.20)
gegeben.
Der erste Term in Gleichung (2.54) entspricht der Anisotropie der induzierten
Polarisation, die aufgrund der Verschiebung der Elektronen durch den Einfluss des
externen elektrischen Feldes auftritt. Der zweite Term beschreibt die Anisotropie der
Orientierungspolarisation, die mit der Orientierung der permanenten molekularen
Dipole in Richtung des Feldes unter Berücksichtigung der Ordnung in der Probe
verknüpft ist.
In durch stäbchenförmige Moleküle gebildeten flüssigkristallinen Phasen nimmt die
Polarisierbarkeitsanisotropie ∆α positive Werte an. Der Beitrag der induzierten
Polarisation zu ∆ε ist also positiv. Das bedeutet, dass nichtpolare Substanzen (µ=0)
eine positive dielektrische Anisotropie besitzen.
Der Beitrag der Orientierungspolarisation ist abhängig von der Größe des
Dipolmoments µ und dem Winkel β zwischen µ und der Moleküllängsachse. Nimmt
der Winkel β die Größe des magischen Winkels von 54,74° ein, trägt das
33
Grundlagen
Dipolmoment gleichermaßen zu ε und ε ⊥ bei. Bei kleineren Werten von β ist der
Beitrag zu ∆ε positiv, für größere Winkel negativ.
Ein starker Dipol in Richtung der Moleküllängsachse (β=0) führt also zu hohen
Werten für ∆ε. Dies ist für Substanzen der Fall, die eine elektronegative Gruppe, wie
z. B. eine Nitrilgruppen parallel zur Moleküllängsachse tragen. Deshalb wurden hier
solche Mesogene für die Untersuchung im elektrischen Feld gewählt.
34
3. Synthese nematischer Polymere und Elastomere
In
der
vorliegenden
Arbeit
sollen
flüssigkristalline
Polymere
und
ihre
korrespondierenden Elastomere hergestellt werden, um sie im Hinblick auf die
Kopplung der flüssigkristallinen Phase an das Polymerrückgrat zu untersuchen. Es
soll der Zusammenhang zwischen der Kopplung und der Vernetzerkonzentration
bzw. der Zusammensetzung des Mesogengemischs geprüft werden. Weiterhin soll
ein im elektrischen Feld orientierbares Elastomer synthetisiert werden.
Alle
verwendeten
Systeme
sind
nematische
Seitenkettensysteme
auf
Polysiloxanbasis. Es wurden zunächst lineare Polymere hergestellt, die anschließend
als dünne Proben präpariert und in einem Magnetfeld orientiert wurden. Die so
erhaltenen Monodomänen wurden in einem separaten Schritt mit Hilfe von UV-Licht
vernetzt.
Grund für die Bevorzugung dieses Systems gegenüber den konventionell
hergestellten Elastomeren aus einer Eintopfreaktion war einerseits die bessere
Möglichkeit zur Kontrolle der Orientierung. Die Beobachtung und Beurteilung der
Orientierung dünner Proben kann mit Hilfe der Mikroskopie erfolgen, was bei den
um einen Faktor zehn dickeren Proben aus der Eintopfreaktion nicht möglich ist.
Außerdem erwartet man durch den statistischen Einbau des Vernetzers eine
homogenere Vernetzungsdichte.
3.1. Nomenklatur der Monomere
Zur besseren Verständlichkeit soll hier die Nomenklatur der verwendeten Mesogene,
des Vernetzers und der hergestellten Polymere und Elastomere erläutert werden.
In Abbildung 3.1 sind die Struktur der verwendeten Mesogene und des Vernetzers
dargestellt. In der Nomenklatur der Mesogenen steht das M für mesogene Gruppe,
35
Synthesen
die durch einen Benzoesäurephenylester aufgebaut wird. Die dahinterstehende Zahl
gibt die Anzahl der Kohlenstoffatome in der Alkylspacerkette an. Dahinter folgt die
Abkürzung der terminalen Gruppe der Mesogene. OCH3 steht für eine entständige
Methoxygruppe, CN für eine endständige Nitrilgruppe.
In der Bezeichnung des Vernetzers steht C11 für eine Alkylkette, die aus elf
Kohlenstoffatomen
besteht.
Die
über
eine
Ethergruppe
daran
gebundene
Benzophenoneinheit wird durch OBP abgekürzt.
O
O
O
O
O
O
O
CN
M3CN
M3OCH3
O
O
O
O
O
O
O
M4OCH3
CN
M4CN
O
O
C11OBP
Abbildung 3.1
Struktur der verwendeten Mesogene und des Vernetzers
3.2. Polymersynthesen
Das allgemeine Synthesekonzept zur Herstellung der linearen Polymere ist in
Abbildung 3.2 gezeigt. Als Polymerrückgrat dient ein Poly(hydrogenmethylsiloxan)
(PHMS) mit einem Polymerisationsgrad von ca. 105 Einheiten. In einer
Hydrosilylierungsreaktion als polymeranaloge Umsetzung wird ein olefinischer
Benzoesäurephenylester als Mesogen und die olefinische Benzophenonverbindung
C11OBP als UV-aktiver Vernetzer an das Polymerrückgrat addiert. Die Reaktion
36
Synthesen
wird in konzentrierter Lösung in absolutiertem, thiophenfreien Toluol durchgeführt.
Als Katalysator dient ein PtCODCl2-Komplex. Das Reaktionsgemisch wird 12-24
Stunden bei 40°C gerührt.
CH3
Si
Mesogen
O
O
Pt-COD-Cl2Katalysator
lineares Polymer
H
PHMS
O
C11OBP
Abbildung 3.2
Konzept zur Herstellung linearer Polymere durch eine
Hydrosilylierungsreaktion
Der Fortschritt der Additionsreaktion wurde durch IR-Spektroskopie detektiert. Es
wurde die Abnahme der Si-H-Schwingungsbande bei einer Wellenzahl von ν=2165
cm-1 beobachtet. Der Abbruch der Reaktion erfolgte, sobald diese Bande nicht mehr
zu sehen war. Zur Trennung des erhaltenen Polymers von nicht umgesetzten
Monomer wurde anschließend mehrmals aus Methanol umgefällt, bis in der
Dünnschichtchromatographie kein Monomer mehr nachweisbar war. Das Polymer
wurde in Benzol aufgenommen, durch Filtrieren von eventuellen Staubpartikeln und
anderen festen Verunreinigungen getrennt und gefriergetrocknet.
Während aller Syntheseschritte wurde auf Lichtausschluss geachtet, um eine
Aktivierung des Vernetzers auszuschließen und so eine vorzeitige Vernetzung des
Systems zu vermeiden.
3.2.1. Polymere mit unterschiedlicher Vernetzerkonzentration
Zur Untersuchung des Einflusses der Vernetzerkonzentration auf die Eigenschaften
der Polymere und Elastomere wurde das in Abbildung 3.1 gezeigte Mesogen
M4OCH3 verwendet. Da diese Polymere im Gegensatz zu den in späteren
37
Synthesen
Abschnitten betrachteten Polymeren nur eine Art von Mesogen enthalten, werden sie
hier auch Homopolymere genannt.
Es wurden sechs verschiedene Polymere hergestellt, in denen der Vernetzer C11OBP
in verschiedenen Konzentrationen zwischen 3 und 10 mol-% eingebaut wurde. Für
diese
Polymere
wurden
die
P1
Bezeichnungen
bis
P6
gewählt.
Die
Zusammensetzung und die DSC-Daten der hergestellten Homopolymere ist in
Tabelle 1 dargestellt.
Die Vernetzerkonzentration hat auf die Glasübergangstemperatur nur einen
geringen Einfluss. Die Werte für Tg liegen für alle Proben in derselben
Größenordnung.
Der
Einfluss
auf
die
Phasenumwandlungstemperatur
ist
gravierender. Mit höherer Vernetzerkonzentration sieht man eine Tendenz zu
geringeren Umwandlungstemperaturen.
Tabelle 1
Zusammensetzung und DSC-Daten der Homopolymere P1 bis P6 und Name der
korrespondierenden Elastomere
mol-% M4OCH3
mol-% C11OBP
Tg [°C]
Tn,i [°C]
Elastomer
97
95
94
93
92
90
3
5
6
7
8
10
11
11
9
9
8
8
92
93
87
82
83
78
E1
E2
E3
E4
E5
E6
P1
P2
P3
P4
P5
P6
3.2.2. Copolymere mit reduzierter Kopplung
Zur Untersuchung der Reduktion der Kopplungskonstanten mit dem Ziel, eine
Kopplungskonstante von U=0 zu erreichen, wurde das Konzept der Herstellung von
Copolymeren verfolgt. Durch geeignete Kombination zweier Mesogene, die einzeln
als Homopolymere eine entgegengesetzte Knäuelkonformation aufweisen, soll eine
Knäuelkonformation erreicht werden, die sphärisch ist. Das Prinzip ist in Abbildung
3.3 dargestellt.
38
Synthesen
M4OCH3
M3OCH3
Abbildung 3.3
Kombinierter Einbau von M4OCH3 und M3OCH3 zum Erreichen einer
sphärischen Knäuelkonformation
Es wurden analog zu den Homopolymeren aufgebaute Copolymere mit den in
Abbildung 3.1 gezeigten Mesogenen M3OCH3 und M4OCH3 hergestellt.
Da sie eine unterschiedliche Anzahl von Alkylspaceratomen aufweisen, haben sie
gemäß des odd-even-Effektes eine entgegengesetzte Ausrichtung bezüglich des
Polymerrückgrates. M4OCH3 orientiert sich parallel dazu, was bei alleinigem
Einbau in ein Polymer zu einer prolaten Knäuelkonformation führt. M3OCH3
orientiert sich senkrecht zum Polymerrückgrat, was eine oblate Konformation zur
Folge
hat.
Durch
Einbau
der
beiden
Mesogene
in
verschiedenen
Konzentrationsverhältnissen ist eine gezielte Steuerung der Knäuelanisotropie in den
Polymeren möglich. Wählt man ein passendes Verhältnis, ist eine sphärische
Knäuelkonformation, wie in Abbildung 3.3 gezeigt, erreichbar.
Es wurden fünf verschiedene Copolymere hergestellt, für die die Bezeichnungen
PCo1 bis PCo5 gewählt wurden. Die Konzentration des Vernetzers C11OBP beträgt
in allen Copolymeren 5 mol-%. Als Referenz wird das Homopolymer P2
herangezogen, das ebenfalls 5 mol-% Vernetzer enthält.
Die Zusammensetzungen der Copolymere und ihre durch DSC ermittelten
Übergangstemperaturen sind in Tabelle 2 zusammengestellt. Die Prozentangabe der
39
Synthesen
Mesogene bezieht sich auf die Zusammensetzung des mesogenen Anteils im
Polymer.
Tabelle 2
P2
PCo1
PCo2
PCo3
PCo4
PCo5
Die
Zusammensetzung und DSC-Daten der untersuchten Copolymere und Namen
der korrespondierenden Elastomere
95 mol-% Mesogen, davon
mol-%
% M4OCH3 % M3OCH3
C11OBP
5
5
5
5
5
5
100
75
50
25
20
10
0
25
50
75
80
90
Glasübergangstemperaturen
der
Tg [°C]
Tn,i [°C]
Elastomer
11
13
18
20
19
19
93
80
78
73
74
74
E2
ECo1
ECo2
ECo3
ECo4
ECo5
Copolymere
sind
im
Vergleich
zum
Homopolymer P2 höher, was auf die verringerte Beweglichkeit der Moleküle
aufgrund des kürzeren Spacers in M3OCH3 im Vergleich zum Mesogen M4OCH3
zurückzuführen ist. Man erkennt außerdem einen deutlichen Abfall der nematischisotropen Phasenumwandlungstemperatur der Copolymere im Vergleich zum
Homopolymer. Die flüssigkristalline Phase wird durch die geringere Flexibilität des
kürzeren Spacers destabilisiert. Das Streben der Mesogene nach paralleler
Ausrichtung bedeutet bei kürzerem Alkylspacer eine stärkere Verformung des
Polymerknäuels, was entropisch ungünstiger ist.
3.2.3. E-Feld-sensitive Copolymere
E-Feld-sensitive Polymere sollen hergestellt werden, indem Mesogene eingebaut
werden, die eine Anisotropie in der Dielektrizitätskonstanten ∆ε>0 aufweisen. Das
bedeutet,
bei
Anlegen
eines
elektrischen
Feldes
Mesogenlängsachsen entlang des elektrischen Feldes.
40
orientieren
sich
die
Synthesen
Ziel der Untersuchung dieser flüssigkristallinen Polymerklasse ist es, ein Polymer zu
synthetisieren, das zu einem im elektrischen Feld orientierbaren Elastomer vernetzt
werden kann. Es wird vermutet, dass dies der Fall ist, wenn das Elastomer ohne
Längenänderung bei der Umwandlung von der nematischen in die isotrope Phase
übergeht.
Wie in Abschnitt 2.7 erläutert, muss eine dielektrische Anisotropie im Mesogen
vorliegen, um es im elektrischen Feld orientieren zu können. Diese ist in den
Mesogenen M3OCH3 und M4OCH3 kaum vorhanden. Durch die Substitution der
endständigen Methoxy- durch eine Nitrilgruppe wird eine positive dielektrische
Anisotropie hervorgerufen, die zu einer Orientierbarkeit der Mesogenlängsachse
parallel
zum
elektrischen
Feld
führt.
Die
zu
M3OCH3
und
M4OCH3
korrespondierenden nitrilsubstituierten Mesogene M3CN und M4CN werden
zusätzlich zu den beiden in die Polymere eingebaut. Alle eingebauten Mesogene sind
in Abbildung 3.1 gezeigt.
Es wurden zwei E-Feld-sensitive Polymere synthetisiert, die jeweils 5 mol-%
Vernetzer enthalten. 10 % des Mesogens einer Alkylkettenlänge wurde als Mesogen
mit Nitrilgruppe eingebaut. PCN1 enthält als Mesogene M4OCH3 und M4CN. Es ist
daher das zum Homopolymer P2 korrespondierende E-Feld-sensitive Polymer.
PCN2 ist analog zum Copolymer PCo5 aufgebaut, da dieses eine Längenänderung
von annähernd null bei der Phasenumwandlung zeigt. Es enthält 90 % Mesogene mit
C3-Alkylspacer
und
10
%
Mesogene
mit
C4-Alkylspacer.
Die
genaue
Zusammensetzung und die DSC-Daten finden sich in Tabelle 3. Zum Vergleich sind
die korrespondierenden Polymere ohne Nitrilgruppen ebenfalls in der Tabelle
aufgeführt.
41
Synthesen
Tabelle 3
Zusammensetzung und DSC-Daten der hergestellten E-Feld-sensitiven Polymer
und deren Referenzpolymere
95 mol-% Mesogen, davon
PCN1
P2
PCN2
PCo5
mol-%
Tg [°C]
Tn,i [°C]
17
11
16
19
99
93
84
74
%M4OCH3 %M4CN %M3OCH3 %M3CN C11OBP
90
10
5
100
5
9
1
81
9
5
90
10
5
Der Glasübergang der beiden E-Feld-sensitiven Polymere PCN1 und PCN2 liegt im
gleichen Bereich. Der Glasübergang von PCN1 ist höher als von dessen
Referenzpolymer P2 ohne nitrilhaltige Mesogene. Die Einführung der Nitrilgruppen
führt wahrscheinlich durch die verstärkten Wechselwirkungen der Mesogene
untereinander
zu
einer
Glasübergangstemperatur
eingeschränkteren
von
PCN2
liegt
Beweglichkeit
der
etwas niedriger
Ketten.
als die
Die
seines
Referenzpolymers PCo5.
Die Phasenumwandlungstemperatur nimmt bei beiden Copolymeren PCN1 und
PCN2 im Vergleich zu P2 bzw. PCo5 zu, was wahrscheinlich ebenfalls auf die
stärkeren Wechselwirkungen der Mesogene untereinander zurückzuführen ist.
Vergleicht man PCN1 und PCN2 untereinander, so nimmt Tn,i mit der Einführung
der Mesogene mit C3-Alkylspacer ab. Grund hierfür ist wahrscheinlich wie in
Abschnitt
3.2.2
diskutiert,
die
eingeschränktere
Flexibitität
des
kürzeren
Alkylspacers.
Die zu PCN1 und PCN2 korrespondierenden Elastomere wurden mit ECN1 und
ECN2 bezeichnet.
42
Synthesen
3.3. Herstellung dünner Monodomänenfilme
3.3.1. Probenpräparation als dünne Filme
Um eine einheitliche Vernetzung der Proben zu gewährleisten, muss das UV-Licht in
der Probe möglichst homogen sein. Da die Mesogene ebenfalls UV-Licht absorbieren
und dadurch eine Abschwächung der Strahlung zum Inneren der Probe hin
stattfindet,
wurden dünne Filme von ca. 20 µm Dicke hergestellt. Die
Probenpräparation erfolgte nach einer von A. Komp entwickelten Methode [31], die in
Abbildung 3.4 skizziert ist. Zunächst wird eine gereinigte Glasplatte mit einer
Opferschicht aus Poly(ethyloxazolin) (PEOx) in einem Spincoatingverfahren
beschichtet. Zwei Streifen einer Spacerfolie von 20 µm Dicke werden anschließend an
zwei gegenüberliegenden Seiten der Glasplatten aufgebracht. Sie dienen dazu, eine
konstante Dicke der Probe über den gesamten Film zu gewährleisten. Zwischen die
beiden Folienstreifen wird das Polymer aufgebracht. Dazu ist es notwendig, die
Glasplatte etwas zu erwärmen, um die Viskosität des Polymers herabzusetzen,
sodass es sich beim Aufsetzen einer zweiten, mit einer PEOx-Opferschicht
versehenen Glasplatte verteilen und bis zur gewünschten Dicke komprimieren lässt.
Wie in den folgenden Abschnitten beschrieben wird, werden die Proben
anschließend im Magnetfeld orientiert, die resultierende Monodomäne mit Hilfe von
UV-Strahlung vernetzt und in destilliertes Wasser gegeben, um die Opferschicht
aufzulösen. Auf diese Weise erhält man einen freistehenden, dünnen Elastomerfilm.
43
Synthesen
Glasplättchen
PEOx-Beschichtung
Spacer-Folie
Spin-Coating
freistehender
Elastomerfilm
PEOx-beschichtetes
Glasplättchen
Polymer
1. Orientierung
2. Vernetzung
3. Wasser
Abbildung 3.4
Probenpräparation als dünne Filme
3.3.2. Orientierung im Magnetfeld
Die Orientierung der Polymere erfolgte im Magnetfeld eines Elektromagneten von
ca. 1,7 Tesla Stärke. Um die bei Raumtemperatur hohe Viskosität der Polymere
herabzusetzen und so eine Orientierung zu ermöglichen, wurde sie bei
Temperaturen
von
Umwandlungstemperatur
ca.
5°C
unterhalb
durchgeführt.
der
Das
nematisch-isotropen
Fortschreiten
des
Orientierungsprozesses wurde mittels Polarisationsmikroskopie unter gekreuzten
Polarisatoren verfolgt. Bei paralleler und senkrechter Stellung der Direktorrichtung
zum Analysator erscheint die vollständig orientierte Probe dunkel zwischen
gekreuzten Polarisatoren. In 45°-Stellung ist ein Intensitätsmaximum der Helligkeit
zu beobachten.
In Abbildung 3.5 a) ist beispielhaft eine Probe gezeigt, die sich einige Stunden im
Magneten befand. Auf der linken Seite ist die Direktorrichtung parallel zum
Analysator, auf der rechten Seite in 45°-Stellung dazu. Es hat schon eine Orientierung
stattgefunden, allerdings sind noch Defektlinien zu sehen. Lässt man die Probe über
Nacht im Magnetfeld, verschwinden die Defektlinien und die Probe liefert ein
Mikroskopbild wie in Abbildung 3.5 b) gezeigt. Es sind keine Defektlinien mehr zu
erkennen.
44
Synthesen
a)
b)
Abbildung 3.5
Beobachtung des Orientierungsprozesses im Polarisationsmikroskop zwischen
gekreuzten Polarisatoren: a) Probe mit Defektlinien nach einigen Stunden im
Magneten in paralleler (links) und 45°-Stellung (rechts) des Analysator; b)
Orientierte Probe in paralleler (links) und 45°-Stellung (rechts) des Analysators
Nachdem die Orientierung der Probe abgeschlossen war, wurden die linearen
Polymere mit Hilfe von UV-Strahlung vernetzt. Dazu bestrahlte man je zweimal 20
Minuten von jeder Seite. Anschließend gab man die Probe in Wasser, um die
Opferschicht zu lösen und einen freistehenden Elastomerfilm zu erhalten.
3.3.3. Vernetzungsreaktion
Als Vernetzer wurde das Benzophenonderivat C11OBP in die linearen Polymere
eingebaut, das durch UV-Strahlung aktiviert werden kann. Die Vernetzung erfolgt
über eine radikalische Reaktion. Das Reaktionsschema ist in Abbildung 3.6 gezeigt.
Durch die UV-Strahlung wird in der Benzophenoneinheit ein Diradikal gebildet,
welches
im
Polymerkette
zweiten
Schritt
abstrahiert.
Es
ein
Wasserstoffatom
resultiert
ein
von
einer
radikalisches
benachbarten
Zentrum
am
Kohlenstoffatom in der Benzophenongruppe und an der Polymerkette. Diese beiden
45
Synthesen
Radikale rekombinieren im dritten Schritt, was zur Verknüpfung der beiden
Polymerketten führt.
O
O
hυ
C
H
OH
Abbildung 3.6
C
OH
C
Vernetzungsreaktion des Benzophenonvernetzers
Anschließend wurden die Proben in destilliertes Wasser gegeben. Innerhalb von drei
bis fünf Tagen hat sich die wasserlösliche PEOx-Schicht aufgelöst und man erhält
den freistehenden Elastomerfilm.
Der Vernetzer wurde von A. Komp synthetisiert und zur Verfügung gestellt.
3.4. Präparation der Proben zur Untersuchung im elektrischen Feld
Die Polymere, die im elektrischen Feld untersucht wurden, wurden zwischen zwei
Glasplatten präpariert, die mit einer dünnen Schicht aus Indium-Zinn-Oxid (ITO)
beschichtet waren. Ein gereinigtes Glasplättchen wurde an den beiden Rändern auf
der beschichteten Seite mit Spacerfolie einer Dicke von 20 µm versehen. Das
Glasplättchen wurde erwärmt und etwas Polymer daraufgegeben. Die Erwärmung
war notwendig, um die Viskosität des Polymers herabzusetzen. Anschließend wurde
ein zweites ITO-beschichtetes Glasplättchen mit der beschichteten Seite zum Polymer
gewandt daraufgelegt, und die Probe zusammengepresst. Nach Erkalten der Probe
46
Synthesen
wurden die beiden Plättchen mit Zweikomponentenkleber zusammengeklebt, damit
sich der Abstand bei Einbringen in das elektrische Feld nicht ändern kann.
Um ein elektrisches Feld an die Probe anlegen zu können, wurden zwei Elektroden
aufgeklebt, die mit einem Wechselspannungsgenerator und einem Verstärker
verbunden
werden
können.
Als
Kleber
wurde
ein
leitfähiger
Zweikomponenetenkleber mit Silberpartikeln benutzt.
Die Probenpräparation ist in Abbildung 3.7 skizziert.
Spacer-Folie
Polymer
ITO-Beschichtung
Glasplättchen
Glasplättchen
Leitender Zweikomponenten-Kleber
mit Ag-Partikeln
ITO-Beschichtung
Zweikomponenten-Kleber
U
Elektroden
Wechselspannungsgenerator
Abbildung 3.7
Probenpräparation für die Untersuchung im elektrischen Feld
47
Synthesen
3.5. Synthese der Mesogene
Insgesamt wurden vier verschiedene Mesogene (M4OCH3, M4CN, M3OCH3 und
M3CN) verwendet. Ihre Synthesewege werden in diesem Abschnitt erläutert.
Quantitative Beschreibungen und Charakterisierung finden sich im Abschnitt 6.1.
3.5.1. M3OCH3
In Abbildung 3.8 ist die Synthese des Mesogens M3OCH3 gezeigt.
O
Br
+
HO
O
K2CO3
KI
Aceton
O
O
O
1
NaOH
Ethanol
O
+
O
HO
O
OH
2
3
DCC
CH2Cl2
DMAP
O
O
O
O
M3OCH3
Abbildung 3.8
Synthesestrategie zur Herstellung des Mesogens M3OCH3
Zunächst wurde eine Williamsonveretherung durchgeführt, in der Allylbromid mit
4-Hydroxybenzoesäuremethylester
zu
4-Allyloxybenzoesäuremethylester
1
umgesetzt wurde. Es folgte die alkalische Verseifung der Methylestergruppe in
48
Synthesen
wässrigem Medium zu 4-Allyloxybenzoesäure 2. Anschließend wurde 2 mit 4Methoxyphenol 3 mit Hilfe von N,N’-Dicyclohexylcarbodiimid (DCC) und 4-N,NDimethylaminopyridin
(DMAP)
statt.
Als Produkt
wird das Mesogen 4-
Allyloxybenzoesäure-4-methoxyphenylester (M3OCH3) erhalten.
3.5.2. M4OCH3
Das Synthesekonzept zur Herstellung des Mesogens M4OCH3 ist in Abbildung 3.9
gezeigt.
O
+
OH
HO
O
PPh3,
THF Azodicarbonsäurediisopropylester
O
O
O
4
NaOH
Ethanol
O
+
O
HO
O
OH
5
3
CH2Cl2
DCC
DMAP
O
O
O
O
M4OCH3
Abbildung 3.9
Synthesekonzept zur Herstellung des Mesogens M4OCH3
Im ersten Schritt erfolgte eine Mitsunobu-Reaktion von 4-Butenol und 4Hydroxybenzoesäuremethylester
zum
4-Butenoxybenzoesäuremethylester
4.
49
Synthesen
Anschließend wurde die methylgeschützte Carbonsäuregruppe mit Hilfe von NaOH
und Ethanol entschützt und man erhielt 4-Butenoxybenzoesäure 5, die im nächsten
Schritt mit 4-Methoxyphenol 3 in einer Kupplungsreaktion mit Hilfe von N,N’Dicyclohexylcarbodiimid
(DCC)
und
4-N,N-Dimethylaminopyridin
(DMAP)
unterzogen wurde. Als Produkt wird das Mesogen 4-But-3-enyloxy-benzoesäure-4methoxyphenylester (M4OCH3) erhalten.
3.5.3. M3CN/M4CN
In Abbildung 3.10 ist das Konzept zur Synthese der beiden Mesogene mit
Nitrilgruppe M3CN und M4CN dargestellt. Die Herstellung der olefinischen
Benzoesäurederivate 2 und 5 wurde analog zu den in den Abschnitten 3.5.1 bzw.
3.5.2 beschrieben Synthesen durchgeführt. Die Mesogene 4-Allyloxybenzoesäure-4cyanophenylester
M3CN
und
4-But-3-enyloxybenzoesäure-4-cyanophenylester
M4CN wurden anschließend in einer Veresterungsreaktion zwischen 2 bzw. 5 und 4Hydroxybenzonitril 6 mit N,N’-Dicyclohexylcarbodiimid (DCC) und 4-N,NDimethylaminopyridin (DMAP) hergestellt.
O
O
+
HO
CN
OH
n
n=1: 2
n=2: 5
6
CH2Cl2
DCC
DMAP
O
O
n
O
CN
n=1: M3CN
n=2: M4CN
Abbildung 3.10
50
Synthesekonzept zur Herstellung der Mesogene M3CN und M4CN
4. Ergebnisse und DiskussionFormel-Kapitel 4 Abschnitt 4
Es
wurden
drei
Arten
von
flüssigkristallinen
Seitenkettenpolymeren
und
-elastomeren synthetisiert und untersucht. Die Ergebnisse werden in diesem Kapitel
gezeigt und diskutiert. Abschnitt 4.1 erläutert die Prinzipien der Auswertung, die bei
den verschiedenen Messmethoden angewandt wurden. Abschnitt 4.2 beschäftigt sich
mit Homopolymeren und -elastomeren, die sich in ihrer Vernetzerkonzentration
unterscheiden. Es soll die Gültigkeit der Landau-de Gennes-Theorie im Bezug auf
die Kopplung der flüssigkristallinen Phase an das Polymerrückgrat in Abhängigkeit
der Vernetzerkonzentration geprüft werden. Im Abschnitt 0 werden Copolymere
und -elastomere mit konstanter Vernetzungsdichte diskutiert, deren Kopplung durch
den Einbau zweier unterschiedlicher Mesogene reduziert ist. Ziel ist die
systematische Reduktion der Kopplungskonstanten bis zu einem Wert von U = 0 . Im
Abschnitt 4.4 werden Polymere und Elastomere untersucht, die im elektrischen Feld
orientierbare Mesogene enthalten. Es soll ein Elastomer synthetisiert werden, das
eine Nullkopplung aufweist und sich im elektrischen Feld orientieren lässt.
4.1. Prinzipien der Auswertung
In diesem Kapitel wird der Weg erläutert, auf dem aus den Parametern, die aus
Messungen zugänglich sind, die
Größen erhalten werden können, die zur
Berechnung der Kopplungskonstanten U benötigt werden.
Die Kopplungskonstante U wird durch die folgende Gleichung (s. Abschnitt 2.6.4)
beschrieben
∂λ
U = E0 ⋅  
 ∂S 
(4.1)
E0 ist der elastische Modul bei der Phasenumwandlungstemperatur, λ die relative
Länge und S der Ordnungsgrad der Probe.
51
Ergebnisse und Diskussion
Sind der E-Modul an der nematisch-isotropen Phasenumwandlung, E0, und die
Änderung der relativen Länge mit dem Ordnungsgrad (∂λ/∂S),wie in den nächsten
beiden Abschnitten beschrieben, ermittelt worden, kann die Kopplungskonstante
nach Gleichung (4.1) berechnet und mit der Konzentration an Vernetzer oder mit
dem Konzentrationsverhältnis der eingesetzten Mesogene in Beziehung gesetzt
werden.
Der Fehler der Kopplungskonstanten, ∆U, wird jeweils durch die Gaußsche
Fehlerfortpflanzung aus dem Fehler des E-Moduls, ∆E0, und dem Fehler der
Steigung, ∆(∂λ/∂S), ermittelt.
4.1.1. Relative Länge als Funktion des Ordnungsgrades
Zur Berechnung der Kopplungskonstanten nach Gleichung (4.1) wird die
Abhängigkeit der relativen Länge λ vom Ordnungsgrad S benötigt. Der Weg, auf
dem die Größe erhalten und die Ableitung berechnet wird, wird im Abschnitt 4.1.1.1
erläutert. Im Abschnitt 4.1.1.2 erfolgt eine Fehlerbetrachtung.
4.1.1.1 Vorgehensweise
Zur Bestimmung der relativen Länge λ in Abhängigkeit vom Ordnungsgrad S
werden die relative Länge λ und der Ordnungsgrad S separat in Abhängigkeit von
der Temperatur bestimmt. Zieht man statt der absoluten Temperatur die reduzierte
Temperatur Tred=T/Tn,i heran, eliminiert man Fehler der absoluten Temperaturen
aufgrund von Ungenauigkeiten in den Temperiereinheiten der verschiedenen
Messapparaturen. Die bei gleicher reduzierter Temperatur gemessenen Werte von λ
und S werden korreliert, man erhält λ als Funktion von S. Da λ und S die gleiche
Änderung mit der Temperatur zeigen, ergibt ihre Auftragung gegeneinander eine
Gerade. Die Steigung der Geraden wird in Gleichung (4.1) eingesetzt.
Das Prinzip der Kombination ist in Abbildung 4.1 dargestellt.
52
Ergebnisse und Diskussion
λ
S
Kombination
1
Tred
Tred
1
λ
S
Abbildung 4.1
Kombinationsprinzip von Thermoelastik- und Doppelbrechungsmessungen
Die
Länge
relative
λ
in
Abhängigkeit
von
der
Temperatur
wird
aus
Thermoelastikmessungen bestimmt (s. Abschnitt 6.6.1.). Den temperaturabhängigen
Ordnungsgrad S erhält man aus Doppelbrechungsmessungen (s. Abschnitt 6.6.2.)
Für
die
Kombination
der
beiden
Messmethoden
ist
es
wichtig,
die
Phasenumwandlungstemperatur von der nematischen in die isotrope Phase in
beiden Messungen nach einer einheitlichen Methode zu bestimmen. Es wird die
relative Länge bzw. die direkt aus der Messung zugängliche Phasenverschiebung der
Probe
gegen
die
absolute
Temperatur
aufgetragen
und
eine
graphische
Differenzierung vorgenommen. Im Bereich der Phasenumwandlung wird die
Ableitungskurve mit einem polynominellen Fit angenähert. Der Grad des Fits wird
jeweils so gewählt, dass der Verlauf der Fitkurve bestmöglich mit der abgeleiteten
Kurve
übereinstimmt.
Das
Maximum
der
Fitkurve
wird
als
Phasenumwandlungstemperatur Tn,i definiert.
Zur Kombination wird die gemessene relative Länge λ aus der Thermoelastik mit
Hilfe von Gleichung (6.1) (s. S. 117) angefittet. Für die reduzierten Temperaturen der
Doppelbrechung werden mit der resultierenden Fitfunktion die entsprechenden
Werte für λ berechnet und gegen die berechneten Werte für den Ordnungsgrad S
aufgetragen.
53
Ergebnisse und Diskussion
Aus der linearen Regression erhält man Werte für die Steigung (∂λ/∂S).
4.1.1.2 Fehlerbetrachtung
Bei der Fehlerabschätzung der Auftragung der relativen Länge λ gegen den
Ordnungsgrad S können Fehler bei der Längenbestimmung der Elastomere und bei
der Bestimmung des Ordnungsgrades vernachlässigt werden. Die Hauptursache des
Gesamtfehlers ist eine fehlerhafte Kombination der Temperaturachsen. Werden die
Phasenumwandlungstemperaturen nicht exakt ermittelt, kommt es zu starken
Verschiebungen in der Auftragung von λ gegen S. Daher werden die Fehlerbalken
ermittelt,
indem
die
Phasenumwandlungstemperatur
für
die
Doppelbrechungsmessung um 1°C in positive und negative Richtung verschoben
werden, und die Auswertung für die so erhaltenen reduzierten Temperaturen
wiederholt wird. Für eine positive Verschiebung liegt die Kurve λ gegen S oberhalb
der eigentlichen Kurve, für eine negative Verschiebung unterhalb.
Der Mittelwert aus der Differenz der beiden Kurven zur eigentlichen Kurve wird als
Fehlerbalken festgelegt.
Als Fehler der Steigung (∂λ/∂S), ∆(∂λ/∂S), wird der Mittelwert der Differenzen der
Fehlerkurvensteigungen zur Steigung der eigentlichen Kurve angenommen.
4.1.2. Elastischer Modul
Um die Kopplungskonstante nach Gleichung (4.1) zu berechnen, ist die Kenntnis des
elastischen Moduls bei der Phasenumwandlungstemperatur, E0, nötig. In Abschnitt
4.1.2.1 wird die Vorgehensweise bei der Bestimmung erläutert, in Abschnitt 4.1.2.2
erfolgt eine Erklärung zur Fehlerberechnung.
54
Ergebnisse und Diskussion
4.1.2.1 Vorgehensweise zur Bestimmung von E0
Der elastische Modul bei der Phasenumwandlungstemperatur, E0, wird aus
Spannungs-Dehnungs-Messungen erhalten. Die direkte Bestimmung bei der
Temperatur Tn,i ist allerdings aufgrund des Prätransformationsverhaltens nicht
möglich. Durch die angelegte Spannung wird eine Ordnung der Mesogene induziert,
und die Phasenumwandlungstemperatur zu höheren Temperaturen verschoben. Der
typische Verlauf des E-Moduls mit der Temperatur ist in Abbildung 4.2 gezeigt. Bei
hohen Temperaturen steigt er linear mit der Temperatur an. Kommt man in den
Bereich der Phasenumwandlung, nimmt die Steigung zu. Den theoretischen Wert
des elastischen Moduls bei der Phasenumwandlungstemperatur, E0, erhält man,
wenn man den E-Modul bei verschiedenen Temperaturen in der isotropen Phase
bestimmt und aus dem linearen Bereich auf eine reduzierte Temperatur Tred=1
extrapoliert.
E
E0
1
Abbildung 4.2
Tred
Bestimmung des E-Moduls bei der Phasenumwandlungstemperatur durch
lineare Extrapolation
Die Werte der E-Moduli in der isotropen Phase werden durch Spannungs-DehnungsMessungen bei verschiedenen Temperaturen bestimmt. Es wird in Abhängigkeit von
der Dehnung eine Kraft detektiert, die unter Verwendung der bekannten Breite und
Dicke der Probe in die korrespondierende nominale Spannung σnom umgerechnet
werden kann. Wie in Abbildung 4.3 gezeigt, wird die Spannung σnom gegen die
relative Länge λ=L/L0 aufgetragen. L ist die aktuelle, absolute Länge der Probe, L0 ist
die absolute Länge der ungedehnten Probe.
55
Ergebnisse und Diskussion
σ
T1>T2>T3
T1
T2
T3
E
λ
Abbildung 4.3
Bestimmung des E-Moduls aus Spannungs-Dehnungs-Messungen bei
verschiedenen Temperaturen
Der E-Modul ist definiert als die Ableitung der wahren Spannung σw nach der
Dehnung (Gleichung (2.9)). Da sich der Querschnitt der Probe bei kleinen
Dehnungen kaum ändert, kann statt der wahren die nominelle Spannung verwendet
werden.
In allen durchgeführten Messungen stieg die nominale Spannung linear mit der
Dehnung an. Eine beispielhafte Kurve ist in Abbildung 4.4 gezeigt.
1,4
1,2
2
0,8
5
σnom [10 N/m ]
1,0
0,6
0,4
0,2
0,0
1,00
1,02
1,04
1,06
1,08
1,10
1,12
1,14
λ
Abbildung 4.4
56
Beispiel einer Spannungs-Dehnungs-Kurve bei konstanter Temperatur in der
isotropen Phase
Ergebnisse und Diskussion
4.1.2.2 Fehlerbetrachtung
Der Fehler der Modulbestimmung bei einer konstanten Temperatur durch die
Auftragung der Spannung gegen die Dehnung wird überwiegend durch die
Schwankungen der gemessenen Kraft bestimmt, die auf Ungenauigkeiten der
Kraftmessdose zurückzuführen sind. Die Fehlerbalken wurden aus der Schwankung
der Kraftwerte ohne Zugbelastung ermittelt.
Als Fehler von E0, ∆E0,wurde die Standardabweichung der linearen Regression
angenommen.
57
Ergebnisse und Diskussion
4.2. Einfluss der Vernetzerkonzentration auf die Kopplung
In der Landau-de Gennes-Theorie wird ein Ausdruck für die Innere Energie eines
nematischen Netzwerks hergeleitet. Dieser enthält im Gegensatz zur Beschreibung
einer
niedermolekularen
Substanz
einen
Term,
der
die
Kopplung
der
flüssigkristallinen Phase an das Polymernetzwerk beschreibt. Die Kopplung wird
durch die Kopplungskonstante U quantifiziert. Die Theorie geht von der Annahme
aus, dass die Kopplung von der Vernetzungsdichte des Elastomers abhängt. Die
Kopplungskonstante soll proportional zur Vernetzungsdichte, also auch zur
Vernetzerkonzentration sein. Diese Annahme sollte durch die systematische
Untersuchung einer Reihe von Elastomeren geprüft werden.
Es wurden aus einem Poly(hydrogenmethylsiloxan), dem Vernetzer C11OBP und
dem Mesogen M4OCH3 sechs lineare Polymere P1 bis P6 mit unterschiedlicher
Vernetzerkonzentration hergestellt. Ihre Zusammensetzung ist in Tabelle 4 gezeigt.
Tabelle 4
Zusammensetzung und DSC-Daten der hergestellten linearen Polymere
mol-% M4OCH3
mol-% C11OBP
Tg [°C]
Tn,i [°C]
97
95
94
93
92
90
3
5
6
7
8
10
11
11
9
9
8
8
92
93
87
82
83
78
P1
P2
P3
P4
P5
P6
4.2.1. Orientierungs- und thermisches Verhalten der linearen Polymere
Zur Ermittlung der flüssigkristallinen Phasen und der Knäuelkonformation wurden
mittels Röntgenstreuung uniaxial verstreckte Fasern untersucht. Als repräsentatives
Beispiel ist in Abbildung 4.5 das Röntgendiffraktogramm des Polymers P3 mit 6 %
Vernetzer gezeigt.
58
Ergebnisse und Diskussion
Zugrichtung
Abbildung 4.5
Typisches Röntgendiffraktogramm der Polymere einer uniaxial verstreckten
Faser (Beispiel P3); der Pfeil deutet in Richtung der Verstreckung
Die Reflexe im Weitwinkelbereich sind typisch für eine nematische Phase. Neben den
Weitwinkelreflexen sind schwache Intensitätsmaxima im Kleinwinkelbereich zu
erkennen. Sie deuten auf das Vorliegen von smektischen Clustern in der nematischen
Phase hin. Es liegt also keine reine nematische, sondern eine cybotaktisch-nematische
Phase vor.
Die Intensitätsmaxima im Weitwinkelbereich liegen senkrecht zur Verstreckungsrichtung. Die Mesogene richten sich demnach parallel zur Zugrichtung aus, es kann
auf eine prolate Knäuelkonformation der Polymerketten geschlossen werden. Aus
den Weitwinkelreflexen kann mit Hilfe der Braggschen Gleichung der laterale
Mesogen-Mesogen-Abstand bestimmt werden. Er liegt für die Polymere P1 bis P6 im
Bereich von 2–3 Å.
Tabelle 4 fasst die thermischen Eigenschaften der hergestellten Polymere zusammen.
Die Glasübergangstemperaturen bleiben im Rahmen der Messgenauigkeit ungefähr
gleich. Bei den Phasenumwandlungstemperaturen von der nematischen in die
isotrope Phase ist eine Tendenz zu kleineren Werten mit zunehmender
Vernetzerkonzentration zu erkennen. Dies ist darauf zurückzuführen, dass der
59
Ergebnisse und Diskussion
Vernetzer nicht flüssigkristallin ist und somit die Ordnung der nematischen Phase
stört. Die Störung ist umso größer, je höher die Konzentration des Vernetzers ist.
4.2.2. Untersuchung der Netzwerke
Die orientierten, linearen Polymere P1 bis P6 wurden durch Bestrahlung mit UVLicht in die korrespondierenden Elastomere E1 bis E6 überführt. Alle Proben wurden
als dünne Monodomänenfilme von ca. 20 µm Dicke hergestellt. Sie wurden
verschiedenen
Charakterisierungsmethoden
unterzogen,
um
die
Beziehung
zwischen Kopplungskonstante und Vernetzerkonzentration zu untersuchen.
Es liegen keine exakten thermischen Daten für die Elastomere vor. Um
aussagekräftige und reproduzierbare Temperaturwerte für die Übergänge zu
erhalten, wird eine gewisse Menge an Probe benötigt, welche durch die nur sehr
geringe Dicke der Probe und die begrenzte Probenfläche nicht aufzubringen war.
Aus
den
DSC-Messungen
konnten
lediglich
grobe
Abschätzungen
der
Übergangstemperaturen vorgenommen werden. Der Glasübergang steigt um ca. 5
bis 10°C an, die nematisch-isotropen Phasenumwandlungstemperaturen sinken um
ca. 20 bis 30°C ab.
4.2.2.1 Spontane Längenänderung
Zur Bestimmung der relativen Länge in Abhängigkeit der Temperatur wurden
Thermoelastikmessungen durchgeführt. Das Mess- und Auswertprinzip ist in
Abschnitt 6.6.1 erklärt.
Die Thermoelastikkurven für die Proben mit unterschiedlichem Vernetzergehalt sind
in Abbildung 4.6 gezeigt. Die relative Länge λ=L/Liso ist gegen die reduzierte
Temperatur Tred=T/Tn,i aufgetragen. Liso ist die Länge der Probe in der isotropen Phase.
60
Ergebnisse und Diskussion
1,25
E1
E2
E3
E4
E5
E6
1,20
λ
1,15
1,10
1,05
1,00
0,85
0,90
0,95
1,00
1,05
1,10
Tred
Abbildung 4.6
Thermoelastikkurven für die Elastomere E1 bis E6 mit verschiedener
Vernetzerkonzentration
Alle Elastomere zeigen eine positive Längenänderung, d. h. sie kontrahieren beim
Übergang von der nematischen in die isotrope Phase. Daraus kann auf eine prolate
Knäuelkonformation geschlossen werden. Dies steht im Einklang mit den
Ergebnissen der Röntgenmessungen der linearen Polymere, sowie dem odd-evenEffekt und der damit zu erwartenden globalen Knäuelkonformation (s. Abschnitte
2.4.1 und 2.4.2.)
Abbildung 4.6 ist außerdem zu entnehmen, dass die spontane Längenänderung λ mit
zunehmender Vernetzerkonzentration abnimmt.
Die Breite der Phasenumwandlung nimmt mit steigender Vernetzerkonzentration
zu. Während bei der Probe E1 mit 3 % Vernetzer die relative Länge entsprechend
einer Phasenumwandlung 1. Ordnung sprunghaft abnimmt, ist der Übergang bei der
Probe E6 mit 10 % Vernetzer kontinuierlich. Die Ursache ist der in Abschnitt 2.6.4
behandelte finite-size-Effekt.
Bei der Probe E6 ist auffällig, dass ab einer reduzierten Temperatur kleiner 0,92 keine
weitere Verlängerung mehr auftritt. Der Grund hierfür ist wahrscheinlich die hohe
Glasübergangstemperatur der Probe. Noch bevor der theoretisch maximale Wert der
61
Ergebnisse und Diskussion
relativen Länge erreicht ist, erstarrt das Elastomer glasartig und kann sich nicht
weiter ausdehnen. Die Länge wird in einem Nicht-Gleichgewichtszustand bestimmt.
Derselbe Effekt ist schwächer ausgeprägt und bei niedrigerer reduzierter Temperatur
beim Elastomer E5 zu finden.
4.2.2.2 Ordnungsgrad
Der
Ordnungsgrad
von
flüssigkristallinen
Elastomeren
wird
meist
durch
Röntgenstreuexperimente bestimmt. Bei Proben geringer Dicke ist dies allerdings
nicht möglich, da die Streuintensität auch bei langer Belichtungszeit zu schwach ist.
Wie in Abschnitt 2.6.3 ausgeführt, ist die Bestimmung des Ordnungsgrades auch mit
Hilfe von Doppelbrechungsmessungen möglich. Die Erläuterung der genauen
Messmethode sowie des Vorgehens bei der Auswertung ist in Abschnitt 6.6.2
gegeben.
Gemäß dem Haller-Plot wurde der natürliche Logarithmus der Doppelbrechung ∆n
gegen den negativen natürlichen Logarithmus von –τ=(Tn,i-T)/Tn,i aufgetragen. Als
Beispiel ist diese Auftragung für die Probe E2 mit 5 % Vernetzer in Abbildung 4.7
gezeigt. Die Extrapolation erfolgte für die Proben E1 bis E4 in einem Bereich
ln(Tn,i/(Tn,i-T)) von 2,0 bis 3,0. In diesem Bereich verläuft die Kurve linear.
62
Ergebnisse und Diskussion
-2,0
-2,2
ln(∆n)
-2,4
-2,6
-2,8
-3,0
-3,2
2,0
2,5
3,0
3,5
4,0
4,5
5,0
5,5
ln(Tn,i/(Tn,i-T))
Abbildung 4.7
Auftragung und Extrapolation nach Haller der Probe E2
Für die Proben E5 und E6 wurde der Bereich zwischen 2,5 und 3,5 festgelegt, da
diese Proben im Bereich von 2,0 bis 2,5 eine veränderte Steigung aufwiesen, was ein
typisches Verhalten bei der glasartigen Erstarrung ist. Der Haller-Plot für die Probe
E6 ist in Abbildung 4.8 gezeigt.
-2,0
-2,2
ln(∆n)
-2,4
-2,6
-2,8
-3,0
-3,2
2,0
2,5
3,0
3,5
4,0
4,5
5,0
5,5
ln(Tn,i/(Tn,i-T))
Abbildung 4.8
Auftragung und Extrapolation nach Haller der Probe E6
63
Ergebnisse und Diskussion
Wie in Abschnitt 2.6.3 erläutert, ist der temperaturabhängige Ordnungsgrad der
Probe als Quotient aus der temperaturabhängigen Doppelbrechung und der
Doppelbrechung bei 0 K, ∆n0, die man aus dem y-Achsenabschnitt der linearen
Extrapolation des Hallerplots erhält, nach Gleichung (2.35) errechenbar.
In Abbildung 4.9 ist der Ordnungsgrad der Proben E1 bis E6 gegen die reduzierte
Temperatur aufgetragen.
0,6
E1
E2
E3
E4
E5
E6
0,5
S
0,4
0,3
0,2
0,1
0,0
0,85
0,90
0,95
1,00
1,05
1,10
Tred
Abbildung 4.9
Temperaturabhängigkeit des Ordnungsgrades der Proben E1 bis E6
Im Verlauf der Kurven in Abbildung 4.9 ist eine Tendenz zu kleineren
Ordnungsgraden
in
der
nematischen
Phase
mit
zunehmender
Vernetzerkonzentration zu sehen. Diese Beobachtung stimmt mit den Ergebnissen
der
Thermoelastikmessungen
überein,
in
denen
die
Längenänderung
mit
zunehmender Vernetzerkonzentration sinkt. Die Ordnung der flüssigkristallinen
Phase wird durch die Anwesenheit des nicht flüssigkristallinen Vernetzers gestört.
Mit höherer Konzentration an Vernetzer ist dies in größerem Ausmaß der Fall.
Der Ordnungsgrad für die Proben E1 bis E5 liegt bei einer reduzierten Temperatur
von Tred=0,88 im Bereich von 0,54 bis 0,59. Das Elastomer E6 stellt wie in der
Thermoelastik eine Ausnahme dar. Bei reduzierten Temperaturen Tred≤ 0,92 steigt der
64
Ergebnisse und Diskussion
Ordnungsgrad nicht weiter an, sondern bleibt bei einem Wert von 0,45, was auf den
Übergang in den Glaszustand zurückzuführen ist.
4.2.2.3 Relative Länge als Funktion des Ordnungsgrades
Aus der Kombination von Thermoelastik- und Doppelbrechungsmessungen (s.
Abschnitt 4.1.1) erhält man die relative Länge λ als Funktion des Ordnungsgrades S.
Als Ergebnis wird für die Proben E1 bis E6 die in Abbildung 4.10 gezeigte
Auftragung erhalten.
Die relative Länge λ verläuft annähernd linear mit dem Ordnungsgrad S.
Abweichungen
vom
linearen
Verhalten
treten
hauptsächlich
bei
kleinen
Ordnungsgraden bzw. im Bereich der Phasenumwandlung auf. Sie sind einerseits
auf das Prätransformationsverhalten zurückzuführen, das eine Abweichung vom
idealen Verhalten zur Folge hat. Andererseits haben Fehler bei der Bestimmung von
Tn,i gerade im Bereich der Phasenumwandlung einen großen Einfluss auf den Verlauf
der Kurven. Die Ermittlung der Fehlerbalken ist in Abschnitt 4.1.1.2 erläutert.
E1
E2
E3
E4
E5
E6
1,25
1,20
λ
1,15
1,10
1,05
1,00
0,0
0,1
0,2
0,3
0,4
0,5
0,6
S
Abbildung 4.10
Relative Länge λ gegen Ordnungsgrad S für die Proben E1 bis E6 durch
Kombination von Thermoelastik und Doppelbrechungsmessungen
65
Ergebnisse und Diskussion
Die Steigungen der Kurven für die Elastomere E1 bis E5 wurden durch lineare
Regression im Bereich des Ordnungsgrades zwischen 0,3 und 0,5 bestimmt. Der
Prätransformationsbereich, bei dem die größten Fehler auftreten, wurde ebenso wie
der Bereich hoher Ordnungsgrade, bei dem häufig schon ein Einfluss des
Glasübergangs festzustellen ist, ausgeschlossen. Für die Probe E6 wurde ein Bereich
von 0,2 bis 0,4 gewählt, da die erreichten Ordnungsgrade bei dieser Probe insgesamt
niedriger sind. Der gewählte Bereich entspricht dem betrachteten Bereich bei den
anderen Proben, da der Prätransformationsbereich und der Bereich mit möglichem
Einfluss des Glasübergangs ebenfalls ausgeschlossen wurde. In Abbildung 4.11 ist
die
Steigung
(∂λ/∂S)
gegen
die
Vernetzerkonzentration
aufgetragen.
Das
Zustandekommen der Fehlerbalken wird in Abschnitt 4.1.1.2 beschrieben.
Die Werte der Steigungen sowie die Fehler sind in Tabelle 5 aufgelistet.
0.5
0.4
dλ/dS
0.3
0.2
0.1
0.0
2
3
4
5
6
7
8
9
10
11
mol-% Vernetzer
Abbildung 4.11
Steigungen (∂λ/∂S) in Abhängigkeit von der Vernetzerkonzentration
Es ist zu erkennen, dass die Steigungen im Rahmen ihres Fehlers gleich sind. Eine
Ausnahme ist die Probe E6 mit 10 % Vernetzer. Die in Abbildung 4.11 eingezeichntet
Gerade stellt den Mittelwert der Steigungen der Proben E1 bis E5 dar und liegt bei
0,384. Zur Mittelwertbildung wurde die Probe E6 außer Acht gelassen.
66
Ergebnisse und Diskussion
4.2.2.4 Elastischer Modul
Die Vorgehensweise zur Ermittlung der elastischen Moduli E in der isotropen Phase
sowie die des elastischen Moduls bei der nematisch-isotropen Phasenumwandlung,
∆E0, ist in Abschnitt 4.1.2.1 beschrieben. Die Fehlerbetrachtung findet sich in
Abschnitt 4.1.2.2.
Die Moduli der Elastomere E1 bis E6 bei verschiedenen Temperaturen in der
isotropen Phase sind in Abbildung 4.12 zu sehen.
E1
E2
E3
E4
E5
E6
5
3
6
E [10 N/m
2
]
4
2
1
0
1,00
1,05
1,10
1,15
Tred
Abbildung 4.12
E-Moduli in der nematischen Phase der Elastomerproben E1 bis E6
Aus Gründen der Übersichtlichkeit sind nur einige Fehlerbalken in das Diagramm
eingezeichnet.
Aus Abbildung 4.12 ist zu erkennen, dass die E-Moduli mit höherer Vernetzerdichte
zunehmen. Ab reduzierten Temperaturen größer 1,05 zeigen sie im Rahmen der
Fehler eine lineare Abhängigkeit von der reduzierten Temperatur. Zur Ermittlung
des E-Moduls bei der Phasenumwandlungstemperatur, E0, wird daher bei den
Elastomeren E2 bis E6 eine lineare Extrapolation in diesem Bereich durchgeführt. Ein
Sonderfall stellt die Probe E1 dar. Durch den geringen Gehalt an Vernetzer ist sie bei
hohen Temperaturen nicht stark belastbar, sondern reißt schnell. Spannungs67
Ergebnisse und Diskussion
Dehnungs-Messungen waren daher bei hohen Temperaturen nicht möglich. Der
lineare Bereich wird bei dieser Probe im Gegensatz zu den übrigen bei viel
niedrigeren Temperaturen erreicht, sodass eine lineare Extrapolation bereits ab einer
reduzierten Temperatur von 1,015 möglich ist. Die resultierenden E0-Werte der
Elastomere E1 bis E6 sind in Tabelle 5 aufgelistet und Abbildung 4.13 dargestellt. Als
Fehler der einzelnen Werte wurde die Standardabweichung der linearen Regression
angenommen. Eine lineare Regression der E0-Werte zeigt, dass die E-Moduli im
Rahmen der Fehler linear mit der Vernetzerkonzentration ansteigen. Aus der
Regression ergibt sich außerdem, dass bei einem Vernetzergehalt von 0 % ein
theoretischer elastischer Modul von E0≈0 erreicht wird.
3,5
3,0
2,0
6
E0 [10 N/m
2
]
2,5
1,5
1,0
0,5
0,0
0
1
2
3
4
5
6
7
8
9
10
11
mol-% Vernetzer
Abbildung 4.13
E-Modul-Werte bei der Phasenumwandlungstemperatur Tn,i durch lineare
Extrapolation aus der isotropen Phase
4.2.2.5 Kopplungskonstante
Aus den Ergebnissen für die Steigung (∂λ/∂S) und den E0-Werten kann die
Kopplungskonstante U nach Gleichung (4.1) berechnet werden. Sie ist in Abbildung
4.14 für die Elastomerproben gegen ihre Vernetzerkonzentration aufgetragen. Die
Fehler errechnen sich aus der Gaußschen Fehlerfortpflanzung unter der Verwendung
der Fehler aus der Bestimmung der Steigung, ∆(∂λ/∂S), und der Modulbestimmung,
68
Ergebnisse und Diskussion
∆E0. Die Werte der Kopplungskonstanten und ihrer Fehler sind in Tabelle 5
zusammengestellt.
1,4
1,2
6
U [10 N/m
2
]
1,0
0,8
0,6
0,4
0,2
0,0
0
1
2
3
4
5
6
7
8
9
10
11
mol-% Vernetzer
Abbildung 4.14
Kopplungskonstanten für die Elastomere E1 bis E6
Man erkennt aus Abbildung 4.14 im Rahmen der Fehler einen linearen
Zusammenhang
zwischen
Kopplungskonstante
und
Vernetzerkonzentration.
Extrapoliert man die Kopplungskonstante auf einen Vernetzergehalt von 0 %, erhält
man eine theoretische Kopplungskonstante von ungefähr null.
Tabelle 5
E1
E2
E3
E4
E5
E6
Ergebnisse für die Elastomerproben E1 bis E6
(∂λ/∂S)
0,391
0,367
0,393
0,376
0,393
0,368
∆(∂λ/∂S)
0,032
0,019
0,012
0,014
0,013
0,010
E0[106N/m2] ∆E0[106N/m2] U[106N/m2] ∆U[106N/m2]
1,04
0,05
0,41
0,05
1,67
0,06
0,61
0,05
1,97
0,07
0,77
0,05
2,37
0,08
0,89
0,06
2,67
0,05
1,05
0,05
3,46
0,01
1,27
0,08
Dieser Zusammenhang wurde in der Landau-de Gennes-Theorie angenommen.
Durch die systematische Untersuchung von Elastomeren mit unterschiedlicher
Vernetzerkonzentration konnte die Annahme experimentell bestätigt werden.
69
Ergebnisse und Diskussion
4.3. Beeinflussung der Kopplung durch Copolymerisation
Die im Abschnitt 4.2 untersuchten Elastomere zeigten bei der Umwandlung von der
nematischen in die isotrope Phase Längenänderungen zwischen 19 und 24 %, die auf
die Knäuelanisotropie aufgrund der Kopplung der Flüssigkristallphase an das
Polymernetzwerk zurückgeführt wurden. Da der odd-even-Effekt beim verwendeten
Mesogen M4OCH3 zu einer prolaten globalen Knäuelkonformation führt,
verringerte sich die Länge der Probe beim Erwärmen.
Es sollte durch die Copolymerisation zweier Mesogene ein Elastomer hergestellt
werden, das eine Kopplungskonstante von U=0 hat, also bei der Phasenumwandlung
keine Längenänderung zeigt. Als eines der Mesogene wurde das schon in Abschnitt
4.2 verwendete M4OCH3 mit einer prolaten Knäuelkonformation verwendet. Als
zweites Mesogen sollte das um eine C-Einheit im Alkylspacer kürzere M3OCH3
eingesetzt werden, das zu einer oblaten Knäuelkonformation führt.
Zur systematischen Untersuchung wurde ausgehend vom M4OCH3-Homopolymer
eine Reihe von Copolymeren und korrespondierenden Coelastomeren mit
steigendem Gehalt an M3OCH3 hergestellt.
4.3.1. Charakterisierung der linearen Polymere
Die
Zusammensetzung
der
verschiedenen
Polymere
ist
in
Tabelle
6
zusammengefasst. Alle Proben enthalten 5 mol-% des Benzophenonvernetzers
C11OBP und 95 % Mesogengemisch. Die Prozentangaben in der Tabelle beziehen
sich auf die prozentuale Zusammensetzung des Mesogengemisches.
70
Ergebnisse und Diskussion
Tabelle 6
Zusammensetzung der synthetisierten Copolymere mit DSC-Daten; alle
Polymere enthalten 5 mol-% des Vernetzers C11OBP
P2
PCo1
PCo2
PCo3
PCo4
PCo5
% M4OCH3
100
75
50
25
20
10
% M3OCH3
0
25
50
75
80
90
Tg [°C]
11
13
18
20
19
19
Tn,i [°C]
93
80
78
73
74
74
Es wurde zudem ein Homopolymer mit M3OCH3 als Mesogen hergestellt. Es gelang
allerdings nicht, dieses im Magnetfeld zu orientieren. Eine mögliche Ursache wird im
Abschnitt 4.3.1.3 diskutiert.
4.3.1.1 Thermisches Verhalten
Die
DSC-Daten
der
linearen
Polymere
finden
sich
in
Tabelle
6.
Die
Glasübergangstemperaturen der Copolymere sind im Vergleich zum Homopolymer
P2 höher, was auf eine verringerte Beweglichkeit der Moleküle aufgrund des
kürzeren Spacers verglichen mit dem Mesogen M4OCH3 schließen läßt. Man
erkennt
außerdem
einen
deutlichen
Abfall
der
nematisch-isotropen
Phasenumwandlungstemperatur der Copolymere mit steigendem Gehalt an
M3OCH3. Die flüssigkristalline Phase wird durch die geringere Flexibilität des
kürzeren Spacers destabilisiert. Die parallele Ausrichtung der Mesogene bedeutet bei
kürzerem Spacer eine stärkere Verformung des Polymerknäuels, was entropisch
ungünstiger ist.
4.3.1.2 Orientierungsverhalten
Zur
Charakterisierung
der
vorliegenden flüssigkristallinen Phase und des
qualitativen Orientierungsverhalten bei Dehnung wurden Röntgenuntersuchungen
71
Ergebnisse und Diskussion
an uniaxial verstreckten Fasern durchgeführt. Die Röntgendiffraktogramme sind in
Abbildung 4.15 gezeigt.
a)
b)
c)
Zugrichtung
d)
e)
Abbildung 4.15
f)
Röntgendiffraktogramme der in vertikaler Richtung verstreckten Polymerfasern
a) P2; b) PCo1; c) PCo2 d) PCo3; e) PCo4; f) PCo5.
Alle Polymere zeigen einen Weitwinkelreflex, wie er für nematische Phasen typisch
ist. Es sind zusätzlich schwache Reflexe im Kleinwinkelbereich zu sehen, die auf
smektische Cluster hinweisen. Wie in den Homopolymeren auch liegt hier eine
cybotaktisch nematische Phase vor.
Bei
dem
Homopolymer
P2
und
dem
Copolymer
PCo1
erkennt
man
Intensitätsmaxima im Weitwinkelbereich senkrecht zur Zugrichtung. Die Mesogene
sind parallel zur Zugrichtung orientiert. Da sich die Polymerknäuel mit ihrem
größeren Trägheitsradius entlang der Verstreckungsrichtung ausrichten, kann auf
eine global prolate Knäuelkonformation geschlossen werden. Ab einem Gehalt von
50 % M3OCH3 im Polymer ist ein anderes Orientierungsverhalten zu erkennen. Die
Intensitätsmaxima der Weitwinkelreflexe liegen hier in der Zugrichtung. Die
72
Ergebnisse und Diskussion
Mesogene sind also senkrecht zur Deformationsrichtung orientiert, was einer global
oblaten Knäuelkonformation entspricht.
Eventuelle
Verkippungen
der
Intensitätsmaxima
aus
der
vertikalen
oder
horizontalen Richtung in den Röntgenstreubildern sind auf Ungenauigkeiten beim
Einbringen der Probe in den Strahlengang zurückzuführen. Die unterschiedlichen
Breiten der Intensitätsmaxima sowie die unterschiedliche Intensität der Signale sind
Folgen der Präparation der Proben. Der genaue Betrag der Deformation sowie die
Dicke der Probe können nicht kontrolliert werden. Die vermessenen Proben haben
sowohl einen unterschiedlichen Verstreckungsgrad als auch unterschiedliche Dicken.
Aus den Intensitätsmaxima lässt sich der laterale Mesogen-Mesogen-Abstand
berechnen. Er liegt für alle Proben im Bereich von ca. 3 Å.
4.3.1.3 β -Addition
Die Hydrosilylierungsreaktion der Polysiloxankette mit dem Mesogen M3OCH3
findet nicht ausschließlich an der endständigen CH2-Gruppe statt. Es kann auch zur
β-Addition kommen. Der Alkylspacer im Polymer wird auf 2 C-Einheiten verkürzt,
d. h. seine Ausrichtung ist nach dem odd-even-Effekt nicht mehr senkrecht, sondern
parallel zur Polymerkette.
Mittels 1H-NMR-Spektroskopie kann der Anteil der in β-Position eingebauten
Mesogene abgeschätzt werden. Als Beispiel ist das Spektrum des Polymers PCo3 in
Abbildung 4.16 gezeigt. Das Signal der entstehenden CH3-Gruppe bei der β-Addition
liegt isoliert bei einer chemischen Verschiebung von 0,8 ppm. Das Integral kann mit
dem Integral eines aromatischen H-Atoms verglichen werden. Dabei muss
berücksichtigt werden, dass die aromatischen H-Atome der Mesogene M3OCH3 und
M4OCH3 gleiche chemische Verschiebungen haben.
73
Ergebnisse und Diskussion
Abbildung 4.16
1
H-NMR-Spektrum des Polymers PCo3
Es wird angenommen, dass der Einbau der Mesogene in dem gleichen Verhältnis
stattfindet, wie es in der Monomermischung vorliegt. Es ergeben sich die in Tabelle 7
aufgelisteten Anteile an β-eingebautem Mesogen. Sie liegen zwischen 7 und 17 %.
Die erhaltenen Werte sind allerdings nur grobe Abschätzungen. Die Signalbreite in
den Spektren von Polymerlösungen ist relativ groß. Damit ist die genaue
Bestimmung der Integrale schwierig. Es wurde ein Fehler bei der Bestimmung des
Anteils der β-Addition von 10 % angenommen. Die Spektren der Proben PCo1 und
PCo4 weisen zusätzlich ein schlechtes Signal-Rausch-Verhältnis auf, wodurch gerade
diese beiden Werte des β-Additionanteils mit einem hohen Fehler behaftet sind. Für
sie wurde ein Fehler von 15 % abgeschätzt.
74
Ergebnisse und Diskussion
Prozentualer Anteil an β -Addition von M3OCH3
Tabelle 7
PCo1
PCo2
PCo3
PCo4
PCo5
β-Addition
16 ± 2%
7 ± 1%
8 ± 1%
17 ± 3%
10 ± 1%
Die β-Addition wird auch als Ursache für den erfolglosen Orientierungsversuch des
M3OCH3-Homopolymers angenommen. Durch die teilweise Verkürzung der
ohnehin schon kurzen Spacerkette eines Teils der Mesogene wird die Orientierung
weiter
erschwert.
Die
Abwesenheit
jeglichen
M4OCH3-Mesogens
bedingt
wahrscheinlich auch das Fehlen von „Orientierungskeimen“ zur kollektiven
Orientierung.
4.3.2. Untersuchung der Elastomere
Die Copolymere PCo1 bis PCo5 wurden im Magnetfeld orientiert und durch
Bestrahlung mit UV-Licht zu ihren korrespondierenden Elastomeren ECo1 bis ECo5
vernetzt. Alle Elastomere wurden als Monodomänenfilme einer Dicke von ca. 20 µm
hergestellt.
4.3.2.1 Spontane Längenänderung
Die spontane Längenänderung wurde durch Thermoelastikmessungen bestimmt.
Die genaue Beschreibung des Verfahrens erfolgt in Abschnitt 6.6.1.
Die relative Länge λ=L/Liso (L: aktuelle absolute Länge, L0: absolute Länge in der
isotropen Phase) in Abhängigkeit der reduzierten Temperatur Tred=T/Tn,i ist in
Abbildung 4.17 gezeigt.
75
Ergebnisse und Diskussion
1,25
E2
ECo1
ECo2
ECo3
ECo4
ECo5
1,20
λ
1,15
1,10
1,05
1,00
0,85
0,90
0,95
1,00
1,05
1,10
1,15
Tred
Abbildung 4.17
Thermoelastikkurven des Elastomers E2 und der Coelastomere ECo1 bis ECo5
Man erkennt eine starke Abnahme der relativen Längenänderung mit Erhöhung des
Gehalts an M3OCH3. Die Werte für λ bei einer reduzierten Temperatur von 0,9 sind
in Tabelle 8 zusammengestellt und in Abbildung 4.18 gegen die Konzentration an
M3OCH3 aufgetragen.
Tabelle 8
Relative Länge bei einer reduzierten Temperatur von Tred=0,9 für die Elastomere
E1 und ECo1 bis ECo5
λ (Tred=0,9)
E2
ECo1
ECo2
ECo3
ECo4
ECo5
1,2
1,13
1,09
1,04
1,02
1,01
Wie in Abbildung 4.18 zu sehen, verläuft die Abnahme der relativen Länge linear mit
dem Gehalt an M3OCH3. Bei Probe ECo5 mit einem Gehalt von 90 % M3OCH3 ist
die Längenänderung nahe 0 %. Die Knäuelkonformation sollte hier annähernd
sphärisch sein. Anhand einer linearen Regression kann man den theoretischen Wert
76
Ergebnisse und Diskussion
der Längenänderung für das Homopolymer, das nur M3OCH3 enthält, berechnen.
Er ergibt sich zu 2 %.
1,20
λ (Tred=0,9)
1,15
1,10
1,05
1,00
0
20
40
60
80
100
% M3OCH3
Abbildung 4.18
Relative Länge einer reduzierten Temperatur von Tred=0,9
Die Ergebnisse aus den Thermoelastikmessungen sind bemerkenswert im Vergleich
mit den Ergebnissen aus den Röntgenmessungen der verstreckten Fasern der
linearen Polymere. Bei den Polymeren ist schon bei einem Gehalt von 50 % M3OCH3
eine Orientierung der Mesogene senkrecht zur Zugrichtung entsprechend einer
oblaten Konformation des Polymers festzustellen. Außerdem scheint die theoretische
Längenänderung von 2 % durch Extrapolation auf 100 % M3OCH3 zu gering. Man
erwartet einen mit den aus M4OCH3 bestehenden Homoelastomeren vergleichbaren
Betrag.
Schon in früheren Arbeiten von Greve[55] wurde für Elastomere, die ausschließlich
M3OCH3 als Mesogen enthielten, gefunden, dass trotz oblater Kettenkonformation
im linearen Polymer die entsprechenden Elastomere eine positive Längenänderung
zeigten. Diese Beobachtung führte Greve auf eine Ausrichtung des Vernetzers in der
Flüssigkristallphase zurück, was zu einer anisotropen Vernetzung führen könnte.
In den Arbeiten von Kniesel[56] wurde die Reduktion der Kopplung in cholesterischen
Systemen untersucht. Auch in diesen Fällen wurde in Coelastomeren trotz hoher
77
Ergebnisse und Diskussion
Konzentration an M3OCH3 kein negativer Thermoelastikeffekt gefunden. Im
Elastomer, das nur aus M3OCH3 als Mesogen bestand, erfolgte eine nur sehr geringe
negative Längenänderung.
Greve und Kniesel führten diese Beobachtungen auf den Vernetzungsschritt zurück.
Durch Ausrichtung des Vernetzers in der Flüssigkristallphase kommt es zu einer
anisotropen Vernetzung.
Eine ähnliche Ursache könnte auch hier vorliegen. Ordnet sich der BenzophenonVernetzer
wie in Abbildung
4.19 gezeigt
entlang
des Direktors in der
Flüssigkristallphase an, könnte die Vernetzung hauptsächlich in der Ebene senkrecht
zum Direktor stattfinden. Das würde bedeuten, die oblaten Knäuel vernetzen in
größerem Maße senkrecht zu ihrem größeren Trägheitsradius als parallel dazu.
Dadurch findet eine „Prolatisierung“ der oblaten Knäuel statt, was in den
Thermoelastikkurven zu einer positiven statt zu der erwarteten negativen
Längenänderung führt.
Inwieweit die Länge des Alkylspacers im Benzophenonvernetzer und somit auch der
odd-even-Effekt einen Einfluss auf die Vernetzung hat, könnte durch Variation der
Spacerkettenlänge untersucht werden.
BP
BP
UV
BP
Abbildung 4.19
78
BP
Schematische Darstellung der anisotropen Vernetzungsreaktion im Falle einer
oblaten Knäuelkonformation im Polymer
Ergebnisse und Diskussion
4.3.2.2 Ordnungsgrad
Die Bestimmung des Ordnungsgrades erfolgte durch Doppelbrechungsmessungen.
Das genaue Messprinzip ist in Abschnitt 6.6.2 beschrieben.
Da die Proben beim Haller-Plot die lineare Region in unterschiedlichen Bereichen der
reduzierten Temperatur aufwiesen, wurde der Fitbereich für die lineare Regression
für jedes Elastomer separat festgelegt. Der Ordnungsgrad in Abhängigkeit von der
reduzierten Temperatur Tred=T/Tn,i für das Homoelastomer E2 und die Coelastomere
ECo1 bis ECo5 sind in Abbildung 4.20 gezeigt.
0,6
E2
ECo1
ECo2
ECo3
ECo4
ECo5
0,5
S
0,4
0,3
0,2
0,1
0,0
0,85
0,90
0,95
1,00
1,05
1,10
Tred
Abbildung 4.20
Ordnungsgrad in Abhängigkeit der reduzierten Temperatur für die Proben E2
und ECo1 bis ECo5
Im Vergleich zum Homoelastomer E2 sind die Ordnungsgrade der Coelastomere
niedriger. Vergleicht man die Coelastomere untereinander, ist die Größe des
Ordnungsgrads ungefähr gleich. Die Kurven der Proben ECo3 und ECo4 flachen bei
reduzierten Temperaturen Tred≤0,92 ab. Dies ist auf den Übergang in den Glaszustand
zurückzuführen. Noch bevor die flüssigkristalline Phase ihren maximal möglichen
Ordnungsgrad erreicht hat, erstarrt das Elastomer glasartig. Die Werte des
Ordnungsgrades bei einer reduzierten Temperatur von Tred=0,9 sind in Tabelle 9
zusammengestellt.
79
Ergebnisse und Diskussion
Tabelle 9
Ordnungsgrade der Proben E2 und ECo1 bis ECo5 bei einer reduzierten
Temperatur von Tred=0,9
E2
ECo1
ECo2
ECo3
ECo4
ECo5
S (Tred=0,9)
0,54
0,49
0,49
0,47
0,45
0,50
Die Abnahme des Ordnungsgrades ist vermutlich auf die erschwerte Orientierung
der eingebauten Mesogene mit kürzerem Alkylspacer zurückzuführen. Die direktere
Anbindung der Mesogene erfordert eine stärkere Deformation des Polymerrückgrats
bei der Orientierung. Hinzu kommt, dass ein Teil der M3OCH3-Mesogene in einer βAddition in das Polymer eingebaut wurde (s. Abschnitt 4.3.1.3). Die um eine
Methylgruppe kürzere Kette ist vermutlich noch schwerer zu orientieren.
80
Ergebnisse und Diskussion
4.3.2.3 Relative Länge als Funktion des Ordnungsgrades
Die relative Länge λ kann mit dem Ordnungsgrad S korreliert werden. Die
Vorgehensweise sowie die Fehlerbetrachtung sind in Abschnitt 4.1.1 erläutert. Die
resultierenden Graphen für die Elastomere E2 und ECo1 bis ECo5 sind in Abbildung
4.21 gezeigt.
E2
ECo1
ECo2
ECo3
ECo4
ECo5
1,25
1,20
λ
1,15
1,10
1,05
1,00
0,0
0,1
0,2
0,3
0,4
0,5
0,6
S
Abbildung 4.21
Relative Länge λ in Abhängigkeit des Ordnungsgrades S für die Elastomere E2
und ECo1 bis ECo4
Die Änderung der relativen Länge λ mit dem Ordnungsgrad S zeigt wie bei den
Homoelastomeren
einen
linearen
Verlauf.
Sie
nimmt
mit
zunehmender
Konzentration von M3OCH3 kontinuierlich ab, bis bei ECo5 eine Steigung von etwa
null erreicht ist.
Zur quantitativen Ermittlung der Steigung (∂λ/∂S) wurden die Kurven im
Ordnungsgradbereich zwischen 0,2 und 0,4 linear angefittet. Im Unterschied zu den
Homoelastomeren wurde ein Gebiet kleiner Ordnungsgrade ausgewählt, da der
maximal erreichte Ordnungsgrad kleiner ist. Die Werte der Steigungen sind in
Tabelle 10 aufgelistet.
81
Ergebnisse und Diskussion
In Abbildung 4.22 ist die Änderung der relativen Länge mit dem Ordnungsgrad
gegen den prozentualen Gehalt an M3OCH3 im Elastomer aufgetragen. Im Rahmen
der Fehler nimmt die Steigung (∂λ/∂S) mit dem Anteil an M3OCH3 linear ab.
0,4
(dλ/dS)
0,3
0,2
0,1
0,0
0
20
40
60
80
100
% M3OCH3
Abbildung 4.22
Änderung der relativen Länge λ mit der Steigung S in Abhängigkeit des Gehalts
an M3OCH3 im Elastomer
4.3.2.4 Elastischer Modul
Zur
Bestimmung
des
elastischen
Moduls
an
der
nematisch-isotropen
Phasenumwandlung, E0, wurden Spannungs-Dehnungs-Messungen in der isotropen
Phase durchgeführt. Die Vorgehensweise sowie die Fehlerbetrachtung sind in
Abschnitt 4.1.2 beschrieben.
Die Auftragung des E-Moduls in Abhängigkeit von der reduzierten Temperatur ist
für die Proben E2 und ECo1 bis ECo3 in Abbildung 4.23 gezeigt.
82
Ergebnisse und Diskussion
E2
ECo1
ECo2
ECo3
2,5
1,5
6
2
E [10 N/m ]
2,0
1,0
0,5
0,0
1,00
1,05
1,10
1,15
Tred
Abbildung 4.23
E-Modul in Abhängigkeit der reduzierten Temperatur für die Proben E2 und
ECo1 bis ECo3
Es ist zu erkennen, dass die E-Moduli der Coelastomere ECo1 bis ECo3 kleiner sind
als der des Homoelastomers. Auch der Anstieg des Moduls mit der reduzierten
Temperatur ist für das Homoelastomer größer. Da die Proben alle die gleiche
Vernetzerkonzentration haben, wäre ein gleiches Verhalten zu erwarten. Die
Abweichung lässt vermuten, dass die Vernetzung in den betrachteten Coelastomeren
nicht den Grad erreicht hat wie im Homoelastomer. Eine andere Ursache könnte im
kleineren Existenzbereich der flüssigkristallinen Phase liegen. Wie schon aus den
DSC-Messungen
der
linearen
Polymere
zu
entnehmen
ist,
wird
der
Temperaturbereich, in dem die nematische Phase vorliegt, mit zunehmendem Anteil
an M3OCH3 kleiner. Es kann daher schon in der isotropen Phase ein Einfluss des
Glasübergangs auftreten. Aufschluss über das wirkliche Existenzgebiet der
nematischen Phase in den Elastomeren könnten DSC-Messungen geben. Um
aussagekräftige und reproduzierbare Temperaturwerte für die Übergänge zu
erhalten, wird eine gewisse Menge an Probe benötigt, welche durch die nur sehr
geringe Dicke der Probe und die begrenzte Probenfläche nicht aufzubringen war. Es
wurden dennoch DSC-Messungen durchgeführt, die allerdings nur Abschätzungen
83
Ergebnisse und Diskussion
der
Übergangstemperaturen
liefern.
Die
Glasübergangstemperaturen steigen
demnach um ca. 5 bis 10°C an. Die nematisch-isotropen Phasenumwandlungstemperaturen sinken um ca. 20 bis 30°C ab. Die Existenzbereiche der nematischen
Phasen werden sehr schmal. Die vermutete Ursache für die niedrigen Moduli der
Coelastomere könnte demnach zutreffen. Eine eindeutige Erklärung kann jedoch
nicht gegeben werden.
Im Verlauf der E-Moduli-Kurven der Coelastomere fehlt zudem die erwartete
deutliche Abnahme des E-Moduls beim Erreichen des Prätransformationsbereichs.
Ursache könnte ebenfalls der relativ kleine Bereich der flüssigkristallinen Phase
zwischen
Glaszustand
und
isotropem
Zustand
sein,
sodass
im
Prätransformationsbereich schon ein Einfluss des Glasübergangs wahrzunehmen ist.
Ab einer reduzierten Temperatur von Tred=1,05 beobachtet man bei allen Proben
einen linearen Anstieg des E-Moduls. Ab dieser Temperatur wurden die Kurven
linear auf eine reduzierte Temperatur von 1,00 extrapoliert. Die so ermittelten Werte
für E0 sind in Tabelle 10 zusammengefasst.
Die E-Moduli als Funktion der reduzierten Temperatur der Elastomere ECo4 und
ECo5 sind in Abbildung 4.24 zu sehen.
2,5
ECo4
ECo5
1,5
6
2
E [10 N/m ]
2,0
1,0
0,5
0,0
1,00
1,05
1,10
1,15
Tred
Abbildung 4.24
84
E-Modul der Elastomere ECo4 und ECo5 in Abhängigkeit von der reduzierten
Temperatur
Ergebnisse und Diskussion
Beide Kurven zeigen eine Abnahme des E-Moduls mit höherer reduzierter
Temperatur bis zu einem Wert von Tred≈1,1. Dies widerspricht den theoretischen
Erwartungen, wonach der E-Modul mit der Temperatur zunehmen sollte, wie es
auch bei E2 und ECo1 bis ECo3 beobachtet wurde. Bei hohen reduzierten
Temperaturen flacht der Verlauf der E-Moduli ab. Sie liegen im Bereich Tred≥1,12 bei
Probe ECo4 im Bereich der E-Moduli der Coelastomere ECo1 bis ECo3. Der Abfall
bei ECo5 ist stärker und führt zu kleineren Werten bei hohen reduzierten
Temperaturen als bei ECo4.
Bei
näherer
verschiedenen
Betrachtung
der
zeitabhängigen
Dehnungsschritten
erkennt
Messung
man
der
Spannung
unterschiedliches
bei
Verhalten
abhängig von der Temperatur, bei der die Messung durchgeführt wurde.
In Abbildung 4.25 sind zu der E-Modul-Kurve des Coelastomers ECo4 die
zeitabhängigen Verläufe der Spannung nach den Dehnungsschritten bei drei
verschiedenen reduzierten Temperaturen gezeigt. Es ist zu erkennen, dass bei einer
Temperatur Tred=1,005, die geringfügig über der Phasenumwandlungstemperatur
liegt, die Spannung der Probe direkt nach dem Dehnungsschritt exponentiell
abnimmt. Eine Approximation des Kurvenverlaufs zeigt, dass es sich um eine
exponentielle Abnahme zweiter Ordnung handelt. Die Relaxation der Probe ist bis
zum nächsten Dehnungsschritt noch nicht abgeschlossen. Die gemessenen Werte für
die Spannung in diesem Temperaturbereich sind keine Gleichgewichtswerte.
Die gleiche Beobachtung wurde für eine reduzierte Temperatur von Tred=1,07
gemacht. Die Relaxation der Probe ist hier schon nicht mehr so stark wie bei
kleineren Werten der reduzierten Temperatur, aber dennoch vor allem bei höheren
Dehnungen sichtbar und bis zur Detektion des Messwertes noch nicht abgeschlossen.
Bei einer reduzierten Temperatur von Tred=1,12 ist kein Spannungsabfall mit der Zeit
mehr zu beobachten. Es kann davon ausgegangen werden, dass die gemessenen
Werte für die Spannung Gleichgewichtswerte sind. Daher wurden für die
Extrapolation auf die reduzierte Temperatur Tred=1 nur Werte der E-Moduli bei
reduzierten Temperaturen Tred>1,12 berücksichtigt.
85
Ergebnisse und Diskussion
2,5
1,5
2,0
1,5
1,5
0,5
1,0
2
σ [10 N/m ]
0,0
0
1000
2000
5
3000
4000
5000
6000
Zeit [s]
1,0
5
2
E [10 N/m ]
5
2
σ [10 N/m ]
1,0
1,5
0,0
2
σ [10 N/m ]
1,0
0,5
0
1000
2000
3000
4000
5000
6000
7000
Zeit [s]
5
0,5
0,5
0,0
0
1000
2000
3000
4000
5000
6000
7000
Zeit [s]
0,0
1,00
1,05
1,10
1,15
Tred
Abbildung 4.25
Zeitabhängige Entwicklung der Spannung für verschiedene reduzierte
Temperaturen für das Coelastomer ECo4
Abbildung 4.26 zeigt die zu Abbildung 4.25 analoge Auftragung für das Coelastomer
ECo5. Auch hier erkennt man im Bereich von Tred≈1,06 eine exponentielle Abnahme
2. Ordnung der Spannung nach Dehnung der Probe. Die Relaxation bei Detektion
des Messwertes ist noch nicht vollständig. Die E-Moduli wurden nicht durch
Messungen
im
thermodynamischen
Gleichgewichtszustand
ermittelt.
Die
Spannungs-Zeit-Kurve für eine reduzierte Temperatur von Tred=1,1 zeigt keine
Relaxation, die Messung erfolgte in diesem Falle im Gleichgewicht. Für die
Extrapolation zur Berechnung von E0 wurden die Werte für Tred>1,12 herangezogen.
86
Ergebnisse und Diskussion
2,5
2,0
1,5
6
5
2
σ [10 N/m ]
0,5
0,0
1,0
1,5
0
1000
2000
3000
4000
5000
Zeit [s]
1,0
5
2
σ [10 N/m ]
2
E [10 N/m ]
1,0
1,5
0,5
0,5
0,0
0
1000
2000
3000
4000
5000
Zeit [s]
0,0
1,00
1,05
1,10
1,15
Tred
Abbildung 4.26
Zeitabhängige Entwicklung der Spannung für verschiedene reduzierte
Temperaturen für das Coelastomer ECo5
Die Abnahme der E-Moduli könnte auch bei den Proben ECo4 und ECo5 auf den
relativ kleinen Temperaturbereich zurückzuführen sein, innerhalb dem die
flüssigkristalline Phase existiert. Aus den stark fehlerbehafteten DSC-Kurven von
ECo4 und ECo5 (vgl. Diskussion von ECo1 bis ECo3) kann abgeschätzt werden, dass
das Temperaturgebiet, in dem die nematische Phase existiert, noch kleiner als bei
ECo1 bis ECo3 ist. Die nematisch-isotropen Übergänge erscheinen nicht mehr als
separate Peaks, sondern werden durch den Übergangsbereich in den glasartigen
Zustand überdeckt.
Für die niedrigen Moduli bei hohen reduzierten Temperaturen für ECo5 im
Vergleich zu den anderen Coelastomeren könnte der
Vernetzungsprozess
verantwortlich sein. Die geringere Flexibilität aufgrund des hohen Anteils von
M3OCH3 erschwert möglicherweise den Vernetzungsprozess, wodurch eine
geringere Vernetzungsdichte bei gleicher Vernetzungszeit erreicht wird.
Für die Coelastomere ECo4 und ECo5 ist der Fehler der Bestimmung von E0
wahrscheinlich größer als derjenige von ECo1 bis ECo3, da für die lineare Regression
weniger Messwerte herangezogen wurden. Zudem ist die Festlegung des
Anfangsbereiches des linearen Anstiegs bereits mit einem Fehler behaftet.
87
Ergebnisse und Diskussion
4.3.2.5 Kopplungskonstante
Aus den Werten für die Änderung der relativen Länge mit dem Ordnungsgrad
(∂λ/∂S) (s. Abschnitt 4.3.2.3) und dem elastischen Modul E0 (s. Abschnitt 4.3.2.4) lässt
sich die Kopplungskonstante nach Gleichung (4.1) berechnen. Die Werte finden sich
in Tabelle 10 und sind in Abbildung 4.27 gegen den prozentualen Gehalt von
M3OCH3 aufgetragen.
0,8
0,4
6
U [10 N/m
2
]
0,6
0,2
0,0
0
20
40
60
80
100
% M3OCH3
Abbildung 4.27
Kopplungskonstante in Abhängigkeit des Gehalts an M3OCH3 in den
Coelastomeren
Die Fehler wurden durch Gaußsche Fehlerfortpflanzung aus dem Fehler des EModuls, ∆E0, und den Fehlern der Steigung, ∆(∂λ/∂S), berechnet.
Die Kopplungskonstante nimmt linear mit dem Gehalt an M3OCH3 ab. Einzige
Ausnahme ist die Kopplungskonstante bei einem M3OCH3-Gehalt von 25 %. Sie
liegt unterhalb des Wertes, der durch die lineare Regression zu erwarten ist. Da die
Steigung (∂λ/∂S) in Abhängigkeit von der M3OCH3-Konzentration keine auffällige
Abweichung von dem Verlauf der aus linearer Regression ermittelten Gerade zeigt
(s. Abbildung 4.22), ist der Grund vermutlich ein fehlerhafter Wert des elastischen
Moduls E0. Der Fehler ist nicht nur auf Schwankungen der E-Moduli in der isotropen
Phase zurückzuführen, die im Fehler von E0 berücksichtigt sind, sondern auch auf
88
Ergebnisse und Diskussion
Ungenauigkeiten bei der Bestimmung jedes einzelnen Wertes von E bei den
einzelnen Temperaturen. Dies könnte z. B. ein Fehler in der Bestimmung der Dicke
der Probe sein.
Tabelle 10
E2
ECo1
ECo2
ECo3
ECo4
ECo5
Ergebnisse für die Coelastomere ECo1 bis ECo5 und das Homoelastomer E2
(∂λ/∂S)
0,381
0,300
0,195
0,086
0,047
0,011
∆(∂λ/∂S)
0,024
0,010
0,013
0,016
0,004
0,001
E0[106N/m2] ∆E0[106N/m2] U[106N/m2] ∆U[106N/m2]
1,67
0,06
0,64
0,06
1,16
0,03
0,35
0,02
1,32
0,07
0,26
0,03
1,47
0,04
0,13
0,03
1,47
0,04
0,07
0,01
1,19
0,05
0,01
0,01
Mit der Probe ECo5, dessen Konzentration an M3OCH3 bei 90 % liegt, ist das
angestrebte
Ziel
einer
Nullkopplung
erreicht
worden.
ECo5
besitzt
eine
Kopplungskonstante, die im Rahmen des Fehlers null ist.
89
Ergebnisse und Diskussion
4.4. E-Feld-sensitive Polymere und Elastomere
Es sollte ein Elastomer hergestellt werden, das sich im elektrischen Feld orientieren
lässt. Hierzu wurde wiederum das System aus Polyhydrogenmethylsiloxan, den
Mesogenen M4OCH3 und M3OCH3 und dem Vernetzer C11OBP verwendet. Um
eine Empfindlichkeit auf elektrische Felder zu schaffen, wurden zusätzlich Mesogene
eingebaut, die statt der terminalen Methoxygruppe eine Nitrilgruppe tragen und
daher eine Dielektrizitätsanisotropie aufweisen. Der Anteil dieser Mesogene beträgt
10 % der gesamten Mesogenmenge.
Es wurden zwei lineare, E-Feld-sensitive Polymere PCN1 und PCN2 hergestellt,
deren Zusammensetzung in Tabelle 11 gezeigt ist. Zum Vergleich finden sich in der
Tabelle die Daten der korrespondierenden Polymere P2 und PCo5 ohne nitrilhaltige
Mesogene. Alle in Tabelle 11 gezeigten Polymere enthalten 5 % des UVinduzierbaren Vernetzers.
Tabelle 11
Zusammensetzung und DSC-Daten der E-Feld-sensitiven Polymere CoCN1 und
CoCN2 und deren Analoga ohne nitrilhaltige Mesogene P2 und Co5
95 mol-% Mesogen, davon
PCN1
P2
PCN2
PCo5
mol-%
%M4OCH3 %M4CN %M3OCH3 %M3CN C11OBP
90
10
5
100
5
9
1
81
9
5
10
90
5
Tg [°C]
Tn,i [°C]
17
11
16
19
99
93
84
74
4.4.1. E-Feld-sensitives Polymer/Elastomer mit C4-Spacer
Es wurde ein Polymer PCN1 und daraus ein Elastomer ECN1 hergestellt, das analog
zu E2 einen Vernetzeranteil von 5 % besitzt und nur aus Mesogenen mit C4-Spacer
(M4OCH3 und M4CN) aufgebaut ist.
90
Ergebnisse und Diskussion
4.4.1.1 Thermisches und Orientierungsverhalten des linearen Polymers
DSC-Messungen
des
linearen
Polymers
PCN1
ergaben
eine
Glasübergangstemperatur von 17°C und eine Phasenumwandlungstemperatur
nematisch-isotrop von 99°C. Beide Werte liegen im Bereich der des Polymers ohne
Nitril-Mesogen, das einen Glasübergang bei 11°C und eine Phasenumwandlung bei
93°C aufweist.
Das Röntgendiffraktogramm einer uniaxial verstreckten Polymerfaser des Polymers
PCN1
ist
in
Abbildung
4.28
zu
sehen.
Es
zeigt
Intensitätsmaxima
im
Weitwinkelbereich senkrecht zur Verstreckungsrichtung. Das lässt auf eine parallele
Orientierung der Mesogene im Bezug auf das Polymerrückgrat schließen. Es liegt
also eine prolate Kettenkonformation vor.
Zugrichtung
Abbildung 4.28
Röntgenstreubild einer verstreckten Faser des Polymers PCN1
4.4.1.2 Spontane Längenänderung des orientierten Elastomers
Nach der Orientierung des Polymers im Magnetfeld und der Vernetzung zum
Elastomer ECN1 unter UV-Licht wurde eine Thermoelastikmessung durchgeführt.
Das Mess- und Auswertprinzip ist in Abschnitt 6.6.1 beschrieben.
91
Ergebnisse und Diskussion
Die resultierende Kurve ist in Abbildung 4.29 gezeigt. Die positive Längenänderung
bei der Umwandlung von der isotropen in die nematische Phase belegt den prolaten
Charakter
der
Netzkettenkonformation,
der
durch
die
Ergebnisse
der
Röntgenstreuung bereits nahe liegt. Der Betrag der Längenänderung ist im Vergleich
zum korrespondierenden Elastomer E2 ohne nitrilhaltige Mesogene etwas geringer.
Bei einer reduzierten Temperatur von 0,9 beträgt die relative Länge für ECN1 λ=1,16
im Gegensatz zu λ=1,20 für E2.
1,20
1,15
λ
1,10
1,05
1,00
0,85
0,90
0,95
1,00
1,05
1,10
Tred
Abbildung 4.29
Thermoelastikkurve des Elastomers ECN1
4.4.1.3 Untersuchung im elektrischen Feld
Zur Untersuchung im elektrischen Feld wurde das lineare Polymer PCN1 zwischen
zwei ITO-beschichtete Glasplatten gebracht (s. Abschnitt 3.4). Die Beobachtung des
Orientierungsverhaltens erfolgte mit Hilfe von orthoskopischer und konoskopischer
Mikroskopie. Die Ausrichtung der Probe im Mikroskop erfolgte so, dass das
elektrische Feld parallel zum Strahlengang lag. Die Mesogene richteten sich damit
parallel zum Strahlengang homöotrop aus. In der Orthoskopie beobachtete man bei
Untersuchung einer Polydomäne bei Anlegen eines elektrischen Feldes eine
Abnahme der Lichtintensität, da die Probe entlang ihrer optischen Achse nicht
92
Ergebnisse und Diskussion
doppelbrechend ist. Die Transmission wurde mit einem Photomonitor in
Abhängigkeit der angelegten Spannung detektiert. Bei der Konoskopie konnte das
Entstehen des typischen Interferenzbildes in Abhängigkeit der elektrischen
Spannung
beobachtet
werden.
In
allen
Fällen
reagierte
die
Probe
ohne
wahrnehmbare zeitliche Verzögerung auf Spannungserhöhung.
Die Messungen der Transmission in Abhängigkeit der angelegten Spannung ist für
verschiedene Temperaturen in Abbildung 4.30 gezeigt. Die Frequenz des
Wechselfeldes betrug 50 Hz.
1,0
80 °C
85 °C
90 °C
Transmission
0,8
0,6
0,4
0,2
0,0
0
20
40
60
80
100
120
Spannung [V]
Abbildung 4.30
Transmission in Abhängigkeit der angelegten Wechselspannung für
verschiedene Temperaturen bei einer Frequenz von 50 Hz für die Probe PCN1
Man erkennt, dass sich die Kurven mit steigender Temperatur zu kleineren
Spannungen verschieben. Der Grund ist vermutlich die abnehmende Viskosität und
damit die steigende Beweglichkeit der Moleküle, die eine Ausrichtung erleichtert.
Die Entwicklung der Orientierung mit der Spannung, die mit der Konoskopie zu
verfolgen ist, ist in Abbildung 4.31 gezeigt. Das charakteristische Kreuzmuster eines
optisch einachsigen Materials bei Betrachtung parallel zur optischen Achse bildet
sich mit steigender Spannung aus.
93
Ergebnisse und Diskussion
Abbildung 4.31
18V
24V
26V
27V
30V
40V
Konoskopiebilder bei steigender Spannung für PCN1 bei 90°C
Zur weiteren Charakterisierung wurde die Transmission der Probe in Abhängigkeit
von der elektrischen Spannung für verschiedene Frequenzen des angelegten
elektrischen Feldes bestimmt. Die Temperatur wurde konstant bei 90°C gehalten. Die
Ergebnisse sind in Abbildung 4.32 aufgetragen. Die Kurven verlaufen alle ähnlich. Es
ist keine Frequenzabhängigkeit des Orientierungsprozesses zu erkennen.
1,0
10Hz
50Hz
95Hz
500Hz
1kHz
Transmission
0,8
0,6
0,4
0,2
0,0
0
10
20
30
40
50
60
70
80
Spannung [V]
Abbildung 4.32
Abhängigkeit der Helligkeit von der Spannung für verschiedene Frequenzen
der Wechselspannung bei einer Temperatur von 90°C für die Probe PCN1
Um Aufschluss über das Orientierungsverhalten des korrespondierenden Elastomers
ECN1 zu erhalten, wurde eine als Polydomäne vernetzte Probe untersucht. Bis zu
94
Ergebnisse und Diskussion
einer Spannung von 140 V bei einer Schichtdicke von 20 µm war keine Orientierung
möglich. Es war auch kein Ansatz einer Orientierung bei unterschiedlichen
Temperaturen zu sehen. Ursache ist vermutlich die Dimensionsänderung, die mit
der Orientierung der Probe einhergeht. Die Probe würde bei der homöotropen
Orientierung dicker. Da die Glasplatten einen definierten Abstand haben und die
Probe durch die Vernetzung fixiert ist, kann sie die notwendige Längenänderung
nicht realisieren. Eine Orientierung ist somit nicht möglich.
4.4.2. E-Feld-sensitives Copolymer/elastomer
Sollte der Grund für die ausbleibende Orientierung des Elastomers ECN1 im
elektrischen
Feld
die
in
Abschnitt
4.4.1.3
vermutete
Einschränkung
der
Dickenänderung sein, könnte das Problem durch Synthese eines Elastomers mit
Nullkopplung umgangen werden.
Es sollten daher die Kopplung und damit die Längenänderung im Elastomer
verringert werden. Es wurde ein zum kopplungsfreien System PCo5/ECo5 mit 90 %
M3OCH3 (s. Abschnitt 4.3.2.5) korrespondierendes Copolymer PCN2 synthetisiert.
10 % des jeweiligen Mesogens wurden durch Mesogene mit endständigen
Nitrilgruppen ersetzt, um eine Orientierung im elektrischen Feld zu ermöglichen.
4.4.2.1 Thermisches und Orientierungsverhalten des linearen Polymers
DSC-Messungen am linearen Polymer PCN2 ergaben einen Glasübergang bei 16°C
und eine Phasenumwandlung nematisch-isotrop bei 84°C. Im Vergleich zum
Polymer PCN1 liegt der Glasübergang fast gleich, die nematisch-isotrope
Phasenumwandlung ist zu niedrigeren Temperaturen hin verschoben.
Röntgenstreuexperimente an einer verstreckten Faser lieferten das in Abbildung 4.33
gezeigte Bild. Aus der Reflexlage parallel zur Zugrichtung ist eine Orientierung der
Mesogene senkrecht dazu und damit eine oblate Netzkettenkonformation abzuleiten.
95
Ergebnisse und Diskussion
Die leichte Verkippung der Maxima aus der Vertikalen ist auf eine nicht exakte
Ausrichtung der Probe im Strahlengang zurückzuführen. Im Vergleich zu den
Röntgenbildern der linearen Polymere ohne nitrilhaltige Mesogene (Abbildung 4.5
und Abbildung 4.15) zeigt PCN2 intensivere Kleinwinkelreflexe, was auf größere
oder höher konzentrierte smektische Cluster in der nematischen Phase hindeutet.
Zugrichtung
Abbildung 4.33
Röntgenstreubild einer in vertikaler Richtung z verstreckten Faser des Polymers
PCN2
4.4.2.2 Spontane Längenänderung des orientierten Elastomers
Das Polymer PCN2 wurde im Magneten orientiert und unter UV-Licht vernetzt. Die
erhaltene Monodomäne wurde zur Ermittlung der spontanen Längenänderung einer
Thermoelastikmessung unterzogen. Die genaue Erläuterung des Mess- und
Auswertprinzips findet sich im Abschnitt 6.6.1.
Die relative Länge λ=L/Liso (L: aktuelle Länge, Liso: Länge in der isotropen Phase) in
Abhängigkeit von der reduzierten Temperatur Tred=T/Tn,i ist in Abbildung 4.34 mit
ECN1 als Vergleich gezeigt.
96
Ergebnisse und Diskussion
1,20
ECN1
ECN2
1,15
λ
1,10
1,05
1,00
0,85
0,90
0,95
1,00
1,05
1,10
Tred
Abbildung 4.34
Thermoelastikkurve für die Proben ECN1 und ECN2
Auch bei ECN2 ist eine geringe positive Längenänderung bei der Umwandlung von
der isotropen in die nematische Phase erkennbar, was auf eine leicht prolate
Netzkettenkonformation hinweist. Dies widerspricht den Erwartungen aufgrund der
Röntgenuntersuchung des entsprechenden Polymers. Dort war wegen der
Orientierung
der
Mesogene
senkrecht
zur
Zugrichtung
auf
eine
oblate
Knäuelkonformation geschlossen worden. Eine mögliche Erklärung kann - wie in
Abschnitt 4.3.2.1 diskutiert - im Vernetzungsprozess liegen. Es ist denkbar, dass sich
der Vernetzer in seiner Ausrichtung an den Mesogenen orientiert. Dadurch wäre ein
Vernetzungsschritt
senkrecht
zur
Achse
des
größeren
Trägheitsradius
wahrscheinlicher als in die anderen Richtungen. Es käme zu einer „Prolatisierung“
der Polymerknäuel.
Die Längenänderung bei der Umwandlung von der nematischen in die isotrope
Phase ist bei ECN2 bedeutend kleiner als bei ECN1, allerdings wird nicht die
gewünschte Längenänderung von null erreicht. Die Knäuelkonformation wird von
den Mesogenen mit Nitrilgruppe anscheinend anders beeinflusst als von den
nitrilfreien Mesogenen. Eine direkte Korrelation ist daher nicht möglich.
97
Ergebnisse und Diskussion
4.4.2.3 Ordnungsgrad
Durch Doppelbrechungsmessungen wurde der Ordnungsgrad der Probe bestimmt.
Das Messprinzip sowie das Vorgehen bei der Auswertung sind in Abschnitt 6.6.2
erläutert.
Die resultierende Kurve ist in Abbildung 4.35 für die Probe ECN2 im Vergleich mit
ECN1 gezeigt. Der Ordnungsgrad für ECN1 in der nematischen Phase ist höher als
für ECN2. Die Fähigkeit zur einheitlichen Ordnung scheint in Anwesenheit von
Mesogenen mit C3-Alkylspacer herabgesetzt zu sein. Verantwortlich dafür ist
vermutlich die geringere Flexibilität des kürzeren Spacers. Außerdem kann auch hier
in einem gewissen Maß die β-Addition des C3-Spacer-Mesogens eine Ursache sein,
durch die sich die Anbindung des Mesogens um eine weitere CH2-Gruppe verkürzt.
Die Phasenumwandlung ist bei ECN2 im Vergleich zu ECN1 verbreitert. Da die
Vernetzerkonzentration gleich ist, ist diese Verbreiterung nicht auf finite-size-Effekte
zurückzuführen. Eine Erklärung kann nicht gegeben werden.
0,7
ECN1
ECN2
0,6
0,5
S
0,4
0,3
0,2
0,1
0,0
0,85
0,90
0,95
1,00
1,05
1,10
Tred
Abbildung 4.35
98
Ordnungsgrad in Abhängigkeit der reduzierten Temperatur für die Proben
ECN1 und ECN2
Ergebnisse und Diskussion
4.4.2.4 Untersuchung im elektrischen Feld
Die Orientierung des Polymers PCN2 in Abhängigkeit von der an die Probe
angelegten elektrischen Spannung wurde anhand der Abnahme der Lichtintensität
bei Betrachtung zwischen gekreuzten Polarisatoren untersucht. Die Probe wurde so
in den Strahlengang gebracht, dass die Richtung des elektrischen Feldes parallel zum
Strahlengang lag. Die Mesogene wurden also homöotrop in Richtung des
Lichtdurchgangs orientiert.
Der Verlauf der Transmission in Abhängigkeit der angelegten Spannung ist in
Abbildung 4.36 für drei unterschiedliche Temperaturen gezeigt.
1,0
72°C
75°C
78°C
Transmission
0,8
0,6
0,4
0,2
0,0
0
20
40
60
80
100
Spannung [V]
Abbildung 4.36
Transmission der Probe in Abhängigkeit der angelegten Spannung für drei
verschiedene Temperaturen
Wie schon für das im Abschnitt 4.4.1.3 betrachtete PCN1 ist der Verlauf der Kurven
temperaturabhängig. Allerdings sind mehrere Unterschiede zu beobachten. Die
Spannung, ab der eine Orientierung zu beobachten ist, liegt bei PCN2 wesentlich
höher. Erst zwischen einer Spannung von 20 und 30 Volt nimmt die Transmission ab.
Außerdem sind die Zeiten, zu denen sich nach Erhöhung der Spannung ein
konstanter Wert der Transmission eingestellt hat, wesentlich länger. Während sich
PCN1 sofort orientierte, lagen die Zeiten bei PCN2 bei bis zu einer halben Stunde.
99
Ergebnisse und Diskussion
Eine Erklärung hierfür könnten die größtenteils kürzeren Alkylspacerketten sein.
Aufgrund der geringeren Flexibilität ist die Orientierung vermutlich erschwert und
findet erst bei höheren Spannungen in geringerer Geschwindigkeit statt.
Ein
weiterer
Unterschied ist
die Entwicklung
der
Schwellspannungen in
Abhängigkeit von der Temperatur. Bei PCN1 nimmt die Schwellspannung mit
Temperaturerhöhung leicht ab. Bei PCN2 hingegen nimmt die Schwellspannung mit
Temperaturerhöhung zu. Die Zunahme der Schwellspannung bei PCN2 ist größer
als die Abnahme bei PCN1.
Die vernetzte Probe ECN2 wurde ebenfalls untersucht. Wie bei ECN1 war bei
verschiedenen Temperaturen und Spannungen bis zu 140 Volt bei einer Schichtdicke
von 20 µm keinerlei Orientierungstendenz zu beobachten.
Der Grund hierfür könnte einerseits darin liegen, dass kein Elastomer erhalten
wurde, welches eine sphärische Knäuelkonformation besitzt. Auch wenn die zur
Knäuelanisotropie proportionale Längenänderung in der thermoelastischen Messung
nur gering ist, reicht sie möglicherweise aus, um eine Orientierung zu verhindern.
Andererseits sind schon beim linearen Polymer PCN2 eine höhere Reaktionszeit auf
angelegte elektrische Spannungen und eine höhere Schwellspannung zu beobachten.
Eventuell wird beides weiter erhöht, wenn man die Probe vernetzt, sodass bei der
hier gewählten Experimentführung keine Orientierung möglich ist.
100
5. Zusammenfassung
Die Phasenumwandlung von der nematischen in die isotrope Phase kann mit der
Landau-de Gennes-Theorie beschrieben werden. Für flüssigkristalline Netzwerke
enthält diese Reihenentwicklung der Freien Energie einen Term, der die
Kopplungskonstante U einschließt, die eine Größe zur Beschreibung der Kopplung
der flüssigkristallinen Phase an das Polymernetzwerk ist. Eine zentrale Annahme der
Landau-de Gennes-Theorie ist, die Kopplungskonstante verhalte sich proportional
zur Vernetzungsdichte. Ob dies tatsächlich der Fall ist, sollte systematisch untersucht
werden, wozu eine Reihe von dünnen Elastomerfilmen hergestellt wurde, die
unterschiedliche Vernetzerkonzentrationen enthielten. Aus der Kombination der
Änderung der relativen Länge und des Ordnungsgrades mit der Temperatur, sowie
aus den elastischen Moduli an der Phasenumwandlungstemperatur wurde die
Kopplungskonstante ermittelt. Sie zeigte eine lineare Abhängigkeit von der
Konzentration des Vernetzers, die von de Gennes gemachte Annahme konnte also an
den hier untersuchten Elastomeren bestätigt werden.
Ein weiteres Ziel dieser Arbeit war, die Kopplungskonstante des Elastomersystems
systematisch zu reduzieren, um schließlich eine Kopplungskonstante von U=0 zu
erreichen. Hierzu wurde neben einem zu einer prolaten Knäuelkonformation
führenden Mesogen ein zweites Mesogen eingesetzt, das gemäß des odd-evenEffektes eine entgegengesetzte Ausrichtung im Bezug auf das Polymerrückgrat hat
und somit zu einer oblaten Konformation des Polymerknäuels aufweist. Die
Konzentration des zweiten Mesogens wurde schrittweise erhöht und die
Kopplungskonstante analog zu den Untersuchungen der Vernetzerkonzentrationsabhängigkeit
bestimmt.
Dabei
war
eine
lineare
Abnahme
mit
steigender
101
Zusammenfassung
Konzentration des zweiten Mesogens zu beobachten. Bei einer Konzentration von 90
% wurde einer Kopplungskonstante von annähernd null erreicht.
Zur Untersuchung des Orientierungsverhaltens im elektrischen Feld wurden
Elastomere
hergestellt,
die
anteilig
aus
Mesogenen
mit
positiver
Dielektrizitätsanisotropie aufgebaut waren. Es sollte überprüft werden, ob die
Orientierung eines Elastomers mit positiver Kopplung im elektrischen Feld möglich
ist. Während sich das korrespondierende lineare Polymer orientieren ließ, war dies
erwartungsgemäß bei der vernetzten Polydomäne nicht möglich. Deshalb wurde
versucht, ein Elastomer mit Nullkopplung zu synthetisieren, wobei sich an den
Ergebnissen der vorigen Untersuchungen zum Konzentrationsverhältnis der zu
oblaten und prolaten Konformationen führenden Mesogene gerichtet wurde. Das so
gewonnene Elastomer wies eine Kopplung auf, die etwas größer als null war.
Untersuchungen des linearen Polymers im elektrischen Feld zeigten eine Fähigkeit
zur Orientierung, allerdings waren die Reaktionszeiten und die Schwellspannungen
wesentlich höher als beim Polymer mit positiver Kopplung. Bei der als Polydomäne
vernetzten Probe war keine Orientierung erreichbar.
In weiterführenden Arbeiten könnte versucht werden, ein E-Feld-sensitives
Elastomer zu synthetisieren, das eine wirkliche Nullkopplung aufweist, und dieses
analog zu analysieren. Des weiteren könnte leichter orientierbare Mesogene
eingebaut werden.
102
6. Experimenteller Teil
Formel-Kapitel 6 Abschnitt 6
6.1. Synthese der Monomere
6.1.1. 4-But-3-enyloxybenzoesäure (M4COOH)
PPh3,
Azodicarbonsäurediisopropylester
O
OH
+
O
O
HO
THF
O
O
NaOH
Ethanol
O
O
OH
M4COOH
Ansatz Veretherung:
35 g (41 ml, 0,48 mol) 3-Buten-1-ol
73 g (0,48 mol) 4-Hydroxybenzoesäuremethylester
126 g (0,48 mol) Triphenylphosphin
100 g (97 ml, 0,48 mol) Azodicarbonsäurediisopropylester
550 ml Tetrahydrofuran getrocknet über Natrium
Durchführung Veretherung:
3-Buten-1-ol, Hydroxybenzoesäuremethylester und Triphenylphosphin wurden
unter Argonatmosphäre in THF vorgelegt und in einem Eis-Kochsalz-Bad auf –5°C
gekühlt. Azodicarbonsäurediisopropylester wurde während 1,5 h langsam zu der
Lösung getropft. Anschließend wurde über Nacht bei Raumtemperatur gerührt. Das
Lösungsmittel
wurde
am
Rotationsverdampfer
entfernt.
Entstandenes
103
Experimenteller Teil
Triphenylphosphinoxid wurde mit 2 l eines Gemischs aus Isohexan/Essigsäureethylester 5:1 ausgefällt und abgesaugt. Bei Lagerung bei 3°C fiel weiteres
Triphenylphosphinoxid
aus,
das
ebenfalls
abgesaugt
wurde.
Das
Lösungsmittelgemisch wurde am Rotationsverdampfer entfernt. Das entstandene
Rohprodukt wurde direkt weiter umgesetzt.
Ansatz Verseifung:
38,4 g (0,96 mol) Natriumhydroxid
165 ml Wasser
450 ml Ethanol
Durchführung Verseifung:
Aus NaOH, Wasser und Ethanol wurde eine Lösung hergestellt, die zum Rückstand
aus der Veretherungsreaktion gegeben wurde. Es wurde zwei Stunden unter
Rückfluss erhitzt. Die Lösung wurde am Rotationsverdampfer etwas eingeengt und
auskristallisiertes Produkt abgesaugt. Die Mutterlauge wurde weiter eingeengt und
auskristallisiertes Produkt abgesaugt. Das Rohprodukt wurde aus Methanol
umkristallisiert.
Ausbeute: 38 g (0,20 mol, 68 % d. Th.)
Charakterisierung:
1
H-NMR (CDCl3): δ/ppm: 2,5 (q, 2H, CH2=CH-CH2), 4,0 (t, 2H, CH2=CH-CH2-CH2),
5,0 (dd, 2H, CH2=CH), 5,8, (m, 1H, CH2=CH), 7,0 (d, 2H,
arom), 7,9 (d, 2H, arom).
104
Experimenteller Teil
6.1.2. 4-But-3-enyloxybenzoesäure-4-methoxyphenylester (M4OCH3)
DCC
DMAP
O
+
O
HO
O
O
O
O
CH2Cl2
OH
M4COOH
O
M4OCH3
Ansatz:
10 g (52 mmol) 4-But-3-enyloxybenzoesäure (M4COOH)
11 g (52 mmol) N,N’-Dicyclohexylcarbodiimid (DCC)
8 g (65 mmol, 1,25 eq) Methoxyphenol
53 mg (416 mmol, 8eq) 4-N,N-Dimethylaminopyridin (DMAP)
250 ml Dichlormethan getrocknet über CaH
Durchführung:
4-But-3-enyloxybenzoesäure und Methoxyphenol wurden zusammen mit DMAP
und ca. 100 ml Dichlormethan unter Argonatmosphäre vorgelegt. DCC wurde im
restlichen Dichlormethan gelöst und unter Eiskühlung zugegeben. Der Ansatz
wurde unter Argonatmosphäre bei Raumtemperatur über Nacht gerührt. Der
gebildete Harnstoff wurde über eine Fritte abfiltriert und die Lösung am
Rotationsverdampfer
eingeengt.
Säulenchromatographie
Anschließend
(Laufmittel
erfolgte
Dichlormethan),
Aufreinigung
gefolgt
von
mittels
dreimaliger
Umkristallisation aus Methanol.
Ausbeute: 10,7 g (36 mmol, 69 % d. Th.)
Charakterisierung:
1
H-NMR (CDCl3): δ/ppm: 2,5 (q, 2H, CH2=CH-CH2), 3,8 (s, 3H, O-CH3),
4,1 (t, 2H, CH2=CH-CH2-CH2), 5,2 (dd, 2H, CH2=CH), 5,8
(m, 1 H, CH2=CH), 6,9 (q, 4H, arom), 7,1 (d, 2H, arom), 8,1
(d, 2H, arom).
105
Experimenteller Teil
6.1.3. 4-But-3-enyloxybenzoesäure-4-cyanophenylester (MC4CN)
DCC
DMAP
O
O
+ HO
OH
O
O
CN
CH2Cl2,
THF
O
CN
M4CN
Ansatz:
8,9 g (46 mmol) 4-But-3-enyloxybenzoesäure (M4COOH)
5,5 g (46 mmol, 1.1 eq.) 4-Hydroxybenzonitril
10,5 g (51 mmol, 1.1 eq.) N,N’-Dicyclohexylcarbodiimid (DCC)
6,2 g (51 mmol, 1.1eq.) 4-N,N-Dimethylaminopyridin (DMAP)
150 ml Dichlormethan getrocknet über CaH
100 ml Tetrahydrofuran getrocknet über Natrium
Durchführung:
4-But-3-enyloxybenzoesäure, DCC und DMAP wurden unter Stickstoffatmosphäre
vorgelegt und in Dichlormethan und THF gelöst. Die Lösung wurde eine Stunde
gerührt. 4-Hydroxybenzonitril wurde in Dichlormethan und THF gelöst langsam
zugetropft und die Reaktionslösung über Nacht gerührt.
Der entstandene Niederschlag wurde abgesaugt. Die organische Phase wurde
zweimal mit je 150 ml 1 N Natriumhydroxidlösung, zweimal mit je 20 ml 0.5 N
Salzsäure und zweimal mit je 20 ml Wasser gewaschen. Die organische Phase wurde
über Magnesiumsulfat getrocknet und das Lösungsmittel am Rotationsverdampfer
entfernt. Die Aufreinigung erfolgte durch dreimaliges Umkristallisieren aus
Methanol.
Ausbeute: 9,1 g (31 mmol, 61 % d. Th.)
106
Experimenteller Teil
Charakterisierung:
1
H-NMR (CDCl3): δ/ppm: 2,6 (q, 2H, CH2=CH-CH2), 4,1 (t, 2H, CH2=CH-CH2-CH2),
5,2 (dd, 2H, CH2=CH), 5,9 (m, 1 H, CH2=CH), 7,0 (d, 2H,
arom), 7,4 (d, 2H, arom), 7,7 (d, 2H, arom), 8,1 (d, 2H,
arom).
6.1.4. 4-Allyloxybenzoesäure (M3COOH)
O
Br
+
HO
O
K2CO3
KI
O
O
Aceton
O
NaOH
Ethanol
O
O
OH
M3COOH
Ansatz Veretherung:
30 g (0,248 mol) Allylbromid
37,8 g (0,248 mol) 4-Hydroxybenzoesäuremethylester
71,4 g (0,51 mol) Kaliumcarbonat
Spatelspitze Kaliumjodid
300 ml Aceton
Durchführung Veretherung:
Allylbromid, 4-Hydroxybenzoesäuremethylester, Kaliumcarbonat und Kaliumjodid
wurden zusammen vorgelegt und in Aceton fünf Stunden unter Rückfluss erhitzt.
Die Mischung wurde über Nacht bei Raumtemperatur weitergerührt. Das
Kaliumcarbonat wurde abfiltriert und das Lösungsmittel am Rotationsverdampfer
107
Experimenteller Teil
entfernt.
Der
Rückstand
wurde
ohne
Aufreinigung
weiter
in
einer
Verseifungsreaktion umgesetzt.
Ansatz Verseifung:
90 ml 3,5 N Natriumhydroxidlösung
300 ml Ethanol
Durchführung Verseifung:
Der Rückstand aus der Veretherungsreaktion wurde mit Natriumhydroxidlösung
und Ethanol versetzt und über Nacht bei 80°C gerührt. Das Ethanol wurde am
Rotationsverdampfer entfernt. Nach Verdünnen der Lösung mit Wasser wurde mit
Salzsäure auf pH 1 angesäuert. Das dabei ausgefallene Produkt wurde abgesaugt
und aus Methanol umkristallisiert.
Ausbeute: 35 g (0,20 mol, 79 % d. Th.)
Charakterisierung:
1
H-NMR (CDCl3): δ/ppm: 4,6 (m, 2H, CH2=CH-CH2), 5,3 (m, 2H, CH2=CH-CH2),
6,0 (m, 1H, H2C=CH-CH2), 7,0 (d, 2H, arom.), 7,9 (d, 2H,
arom.).
108
Experimenteller Teil
6.1.5. 4-Allyloxybenzoesäure-4-methoxyphenylester (M3OCH3)
DCC
DMAP
O
HO
O
O
O
O
CH2Cl2
OH
M3COOH
O
O
M3OCH3
Ansatz:
7,6 g (42 mmol) 4-Allyloxybenzoesäure (M3COOH)
8,7 g (42 mmol) N,N’-Dicyclohexylcarbodiimid (DCC)
6,6 g (53 mmol, 1,25 eq) Methoxyphenol
42 mg (344 mmol, 8 eq) 4-N,N-Dimethylaminopyridin (DMAP)
200 ml Dichlormethan getrocknet über CaH
Durchführung:
4-Allyloxybenzoesäure und Methoxyphenol wurden zusammen mit DMAP und ca.
100 ml Dichlormethan unter Argonatmosphäre vorgelegt. DCC wurde im restlichen
Dichlormethan gelöst und unter Eiskühlung zugegeben. Der Ansatz wurde unter
Argonatmosphäre bei Raumtemperatur über Nacht gerührt. Der gebildete Harnstoff
wurde abfiltriert und die Lösung am Rotationsverdampfer eingeengt. Die
Aufreinigung erfolgte durch fünfmalige Umkristallisation aus Methanol.
Ausbeute: 6,0 g (21 mmol, 50 % d. Th.)
Charakterisierung:
1
H-NMR (CDCl3): δ/ppm: 3,8 (s, 3H, O-CH3), 4,1 (t, 2H, CH2=CH-CH2), 5,2 (dd, 2H,
CH2=CH), 5,8, (m, 1 H, CH2=CH-CH2), 6,9 (q, 4H, arom),
7,1 (d, 2H, arom), 8,1 (d, 2H, arom).
109
Experimenteller Teil
6.1.6. 4-Allyloxybenzoesäure-4-cyanophenylester (M3CN)
O
+
O
HO
CN
OH
1. SOCl2, DMF
2. Triethylamin,
O
O
O
CH2Cl2
M3COOH
CN
M3CN
Ansatz Säurechlorid:
10,0 g (56 mmol) 4-Allyloxybenzoesäure (M3COOH)
33,3 g (20,3 ml, 280 mmol, 5 eq) Thionylchlorid
2 Tropfen Dimethylformamid
Durchführung Säurechlorid:
4-Allyloxybenzoesäure, frisch destilliertes Thionylchlorid und Dimethylformamid
wurden zwei Stunden unter Rückfluss erhitzt. Überschüssiges Thionylchlorid wurde
im Hochvakuum entfernt. Es entstand eine gelbe Flüssigkeit, die ohne weitere
Aufreinigung weiter umgesetzt wurde
Ansatz Veresterung:
8,0 g (70 mmol, 1,25 eq) 4-Hydroxybenzonitril
7,0 g (9,6 ml, 70 mmol, 1,25 eq) Triethylamin
40 ml Dichlormethan (über Molsieb 4 Å getrocknet)
Durchführung Veresterung:
4-Hydroxybenzonitril wurde zusammen mit Triethylamin in Chloroform gelöst.
Unter Eiskühlung wurde das Produkt aus der Säurechloridherstellung langsam
zugetropft. Die Mischung wurde bei Raumtemperatur über Nacht gerührt.
Entstandener Niederschlag wurde abfiltriert und mit Dichlormethan gewaschen. Das
Lösungsmittel
110
wurde
am
Rotationsverdampfer
entfernt.
Aufreinigung
des
Experimenteller Teil
Rohprodukts erfolgte durch zweimalige Umkristallisation aus Methanol und
anschließende Säulenchromatographie (Petrolether/Essigsäureethylester 5:1).
Ausbeute: 7,6 g (27,1 mmol, 49 % d. Th.)
Charakterisierung:
1
H-NMR (CDCl3): δ/ppm: 4,6 (dt, 2H, CH2=CH-CH2), 5,4 (dd, 2H, CH2=CH),
6,1, (m, 1 H, CH2=CH-CH2), 7,0 (d, 2H, arom),
7,3 (d, 2H, arom), 7,7 (d, 2H, arom), 8,1 (d, 2H, arom).
6.2. Synthese des Vernetzers
Der Vernetzer wurde von A. Komp synthetisiert und freundlicherweise zur
Verfügung gestellt.
6.3. Synthese der linearen Polymere
Bei der Synthese, Aufreinigung und Aufbewahrung der Polymere wurde auf
Lichtausschluss geachtet, um eine ungewollte Aktivierung des UV-empfindlichen
Benzophenon-Vernetzers zu verhindern und eine vorzeitige Vernetzungsreaktion zu
vermeiden.
111
Experimenteller Teil
6.3.1. Zusammensetzung
Die Zusammensetzung der einzelnen Polymere ist in Tabelle 12 aufgeführt.
Tabelle 12
Zusammensetzung der synthetisierten und untersuchten linearen Polymere
Zusammensetzung des Mesogenanteils
P1
P2
P3
P4
P5
P6
PCo1
PCo2
PCo3
PCo4
PCo5
PCN1
PCN2
% M4OCH3 % M4CN % M3OCH3
100
100
100
100
100
100
75
25
50
50
25
75
20
80
10
90
90
10
9
1
81
mol-%
% M3CN
9
C11OBP
3
5
6
7
8
10
5
5
5
5
5
5
5
6.3.2. Durchführung der Synthese
Poly(hydrogenmethylsiloxan) mit einem Polymerisationsgrad von ca. 105, Mesogene
und Vernetzer wurden zusammen eingewogen und in ca. 1,5 ml trockenem,
thiophenfreiem
Toluol
gelöst.
Es
wurden
20
ml
einer
1
M
PtCODCl2-
Katalysatorlösung zugegeben und die Reaktionslösung bei 40°C über Nacht gerührt.
Die Reaktionskontrolle erfolgte über IR-Spektroskopie. War die für die Si-H-Bindung
typische IR-Bande bei 2160 cm-1 nicht mehr im Spektrum sichtbar, wurde die
Reaktion abgebrochen. War sie noch vorhanden, wurden weitere 10 µl der
Katalysatorlösung zugegeben und weitere 3-6 Stunden bei 40°C gerührt.
Aufreinigung erfolgte über mehrmaliges (5-7 mal) Umfällen aus Methanol, bis das
Polymer von unreagiertem Monomer befreit war. Die Kontrolle erfolgte über
Dünnschichtchromatographie. Das Polymer wurde in Benzol gelöst, durch einen
Millipore-Filter (45 µm) filtriert und gefriergetrocknet.
112
Experimenteller Teil
6.4. Präparation der dünnen Filme
Die Präparation der dünnen Filme ist in Abbildung 6.1 skizziert. Die einzelnen
Schritte werden im Folgenden beschrieben.
6.4.1. Vorbereitung der Glasplatten
Glasobjektträger wurden in quadratische Stücke mit einer Seitenlänge von 2,5 cm
geschnitten. Die Plättchen wurden jeweils zehn Minuten im Ultraschallbad
nacheinander in Aceton, Methanol und Toluol gereinigt. Die getrockneten
Glassubstrate wurden zweimal durch Spincoating (3000 Umdrehungen pro Minute)
mit je 5 Tropfen einer Lösung (5 Gewichts-%) von Poly(2-ethyl-2-oxazolin) (PEOx)
beschichtet.
6.4.2. Präparation der dünnen Polymerproben
Auf das PEOx-beschichtete Glassubstrat wurde an zwei gegenüberliegenden
Rändern je ein Streifen einer Spacer-Folie von 20 µm Dicke aufgebracht. Das Polymer
wurde im erwärmten Zustand auf das ebenfalls erwärmte Substrat aufgebracht, eine
zweite Substratplatte daraufgelegt und die Platten zusammengepresst.
6.4.3. Orientierung der Polymerproben im Magnetfeld
Die Proben wurden zur Orientierung bei einer Temperatur von fünf bis zehn Kelvin
unter ihrer nematisch-isotropen Phasenumwandlungstemperatur in das Magnetfeld
eines Elektromagneten der Stärke 1,7 Tesla gebracht und so lange darin belassen, bis
die Orientierung einheitlich und ohne Fehlstellen war (ca. 24 h). Der Verlauf des
Orientierungsprozesses und die Qualität der Orientierung wurden mit Hilfe der
Orthoskopie beobachtet. War die Probe bei Betrachtung unter gekreuzten
113
Experimenteller Teil
Polarisatoren und Direktorrichtung parallel zum Analysator einheitlich schwarz,
und waren keine Defektlinien mehr zu sehen, wurde sie aus dem Magneten entfernt.
6.4.4. Herstellung der freistehenden Elastomerfilme
Die Vernetzung der orientierten Polymere erfolgte durch Bestrahlung mit UV-Licht.
Die Probe wurde von jeder Seite zweimal 20 Minuten belichtet. Anschließend wurde
die Probe in Wasser gelegt. Nach ca. 3-5 Tagen löste sich die PEOx-Opferschicht auf
und man erhielt freistehende Elastomerfilme.
Glasplättchen
PEOx-Beschichtung
Spacer-Folie
Spin-Coating
freistehender
Elastomerfilm
PEOx-beschichtetes
Glasplättchen
Polymer
1. Orientierung
2. Vernetzung
3. Wasser
Abbildung 6.1
Präparation der dünnen Filme
6.5. Präparation der Proben zur Untersuchung im elektrischen Feld
Mit Indium-Zinn-Oxid (ITO) beschichtete Glasplättchen wurden im Ultraschallbad
jeweils zehn Minuten nacheinander in Aceton, Methanol und Toluol gereinigt. Ein
gereinigtes Glasplättchen wurde an zwei gegenüberliegenden Rändern auf der
beschichteten Seite mit Spacerfolie einer Dicke von 20 µm versehen. Das
Glasplättchen wurde erwärmt, und es wurde etwas Polymer daraufgegeben. War die
Viskosität des Polymers niedrig genug, wurde ein zweites gereinigtes, ITObeschichtetes Glasplättchen mit der beschichteten Seite zum Polymer gewandt
114
Experimenteller Teil
daraufgelegt und die Probe zusammengepresst. Nach Erkalten der Probe wurden die
beiden Plättchen mit Zweikomponentenkleber zusammengeklebt, damit sich der
Abstand bei Einbringen in das elektrische Feld nicht ändert.
Um ein elektrisches Feld an die Probe anlegen zu können, wurden zwei Elektroden
aufgeklebt, die mit einem Wechselstromgenerator und einem Verstärker verbunden
werden konnten. Als Kleber wurde ein leitfähiger Zweikomponenetenkleber mit
Silberpartikeln benutzt.
Die Präparation der Proben zur Untersuchung im elektrischen Feld ist in Abbildung
6.2 skizziert.
Polymer
Spacer-Folie
ITO-Beschichtung
Glasplättchen
Glasplättchen
Leitender Zweikomponenten-Kleber
mit Ag-Partikeln
ITO-Beschichtung
Zweikomponenten-Kleber
U
Elektroden
Wechselspannungsgenerator
Abbildung 6.2
Präparation der Proben zur Untersuchung im elektrischen Feld
6.6. Untersuchungs- und Auswertmethoden und dazugehörige Geräte
In diesem Abschnitt werden die angewendeten Untersuchungsmethoden mit den
dazugehörigen Geräten erklärt und die Auswertungen erläutert.
115
Experimenteller Teil
6.6.1. Thermoelastik-Messungen
Die Thermoelastikmessungen wurden in einer im Arbeitskreis entwickelten
Apparatur durchgeführt. Die Probe wurde am oberen und unteren Ende mit einem
schwarzen Tesastreifen beklebt und in einer Glassäule aufgehängt, die durch einen
Thermostaten temperierbar war. Die Temperaturmessung erfolgte mit Hilfe eines
Pt100-Thermofühlers im Innenraum der Glassäule, wo sich auch die Probe befand.
Aus der isotropen Phase wurde in Schritten von 2°C in die nematische Phase
abgekühlt. Nach einer Equilibrierungszeit von 3000 Sekunden wurde bei jeder
Temperatur mit Hilfe einer digitalen Kamera ein Foto aufgenommen.
Die Bilder konnten unter Verwendung eines Computerprogramms ausgewertet
werden, das die Länge der Probe über den Kontrast zwischen hellen Bereichen der
Probe und schwarzen Bereichen der Tesastreifen bestimmte.
Die Länge der Probenstreifen betrug ca. 20 mm, die Breite ca. 2 mm.
Die in der Arbeit gezeigten Thermoelastikkurven zeigen eine Auftragung der
relativen Länge gegen die reduzierte Temperatur. Die relative Länge wurde
berechnet aus der vom Auswertprogramm ermittelte absoluten Länge der Probe bei
der bestimmten Temperatur bezogen auf die ermittelte Minimallänge in der
isotropen Phase.
Die reduzierte Temperatur ist die gemessene Temperatur geteilt durch die
nematisch-isotrope
Phasenumwandlungstemperatur.
Die
Phasenumwandlungs-
temperatur wurde folgendermaßen ermittelt. Die relative Länge λ wurde gegen die
absolute Temperatur aufgetragen und die graphische Ableitung gebildet. Im Bereich
der Phasenumwandlungstemperatur wurde die Ableitungskurve mit Hilfe eines
polynominellen Fits angepasst. Der Grad des Fits wurde so gewählt, dass die
Übereinstimmung der Fitkurve mit den Messwerten bestmöglich war. Das
Maximum der Fitkurve wurde als Phasenumwandlungstemperatur Tn,i definiert.
Zur Kombination von Thermoelastik und Doppelbrechungsmessungen ist es
notwendig, eine Funktion für die relative Länge λ in Abhängigkeit von der
116
Experimenteller Teil
reduzierten Temperatur zu haben. Als Fitfunktion für den flüssigkristallinen Bereich
eignet sich ein Polynom zweiten Grades, das oberhalb der Phasenumwandlung
durch eine sigmoidale Funktion ausgeblendet wird. Die Fitfunktion über den
gesamten Temperaturbereich λfit besteht aus drei Faktoren, die die flüssigkristalline
Phase (flc), die Ausblendung(fsig) und den linearen Verlauf der Dehnung mit der
Temperatur für ein isotropes Elastomer (flin) beschreiben.
λ fit = ( flc ⋅ f sig + 1) ⋅ flin
(6.1)
Die sigmoidale Ausblendfunktion mit den Parametern T0 und T1 lautet
f sig ( T ) =
1

 T − T0  
 1 + exp 

 T1  

(6.2)
Für große Temperaturen T>>T0 geht dies Funktion gegen null. Für kleine
Temperaturen T<<T0 geht sie gegen 1.
Der lineare Term ist gegeben durch
flin (T ) = a + b ⋅ T
(6.3)
mit den Fitparametern a und b.
Zur Beschreibung des flüssigkristallinen Anteils wird ein Polynom zweiten Grades
benutzt.
flc (T ) = c + d ⋅ T + e ⋅ T 2
(6.4)
mit den Fitparametern c, d und e.
6.6.2. Doppelbrechungsmessungen
Die Doppelbrechungsmessungen wurden ebenfalls in einer im Arbeitskreis
entwickelten Apparatur durchgeführt. Die Doppelbrechung wird dabei nicht direkt
bestimmt, sondern aus der Phasenverschiebung ∆ϕ ermittelt, die ein linear
polarisierter Laserstrahl beim Passieren der Probe durch die Anisotropie der
Brechungsindizes erfährt. Der schematische Aufbau der Apparatur ist in Abbildung
6.3 gezeigt.
117
Experimenteller Teil
Iz
Iz
Iz
β
Ix
Abbildung 6.3
Ix
Ix
Schematischer Aufbau der Apparatur zur Bestimmung der Doppelbrechung
Die Probe befindet sich in einer temperierbaren Zelle. Der Direktor ist in vertikaler
Richtung ausgerichtet. Ein He-Ne-Laser der Wellenlänge 632 nm wird durch einen
Polarisator im Winkel von 45° zum Direktor der Probe polarisiert, bevor er die Probe
durchdringt. Aufgrund der unterschiedlichen Ausbreitungsgeschwindigkeiten der
beiden Komponenten senkrecht und parallel zum Direktor der Probe entsteht aus
dem linear polarisierten Licht elliptisch polarisiertes Licht, wenn es die Probe
passiert. Das elliptisch polarisierte Licht wird durch ein λ/4-Plättchen wieder in
linear polarisiertes Licht umgewandelt, dessen Polarisationsrichtung im Vergleich
mit dem ursprünglichen Strahl um einen gewissen Winkel β gedreht ist.
Detektion erfolgt über eine Photodiode unter Verwendung des Prinzips des
drehenden Analysators[57]. Es wird die Phasenverschiebung ∆ϕ des in der Photodiode
erzeugten Sinussignals im Vergleich zu einem Referenzsignal gemessen, das durch
einen synchron mit dem Analysator drehenden Propeller und einer Lichtschranke
erzeugt wird. Die Phasenverschiebung ∆ϕ ist das Doppelte des Winkels β, um den
die Ebene des linear polarisierten Lichts gedreht wird.
118
Experimenteller Teil
Aus der Phasenverschiebung ∆ϕ wird die Doppelbrechung mit Hilfe von folgender
Gleichung berechnet.
∆n =
λ
⋅ ∆ϕ
2 ⋅π ⋅ d
(6.5)
λ ist die Wellenlänge des Laserstrahls, der die Probe passiert, und d ist die Dicke der
Probe.
Die Änderung der Dicke der Probe bei der Umwandlung von der isotropen in die
nematische Phase muss bei der Berechnung der Doppelbrechung durch die
Einbeziehung eines temperaturabhängigen Faktors berücksichtigt werden. Dieser
Faktor wird aus der Thermoelastikmessung der entsprechenden Probe erhalten. Die
Dicke der Probe ändert sich umgekehrt proportional zur Wurzel aus der
Längenänderung. Der Faktor f, mit dem man die bei Raumtemperatur gemessene
Dicke der Probe multiplizieren muss, ergibt sich als Quotient der Wurzel des
kleinsten Wertes für λ, λmin, und der Wurzel des Wertes für λ bei der Temperatur, für
die f bestimmt werden soll.
f=
λ min
λ
(6.6)
Genau genommen müsste statt λmin der Wert für λ bei der Temperatur eingesetzt
werden, bei der auch die Dickenbestimmung stattgefunden hat. Da die
Temperaturen
fast
gleich
und
die
Schwankungen
für
λ
für
diesem
Temperaturbereich nur sehr gering sind, wird diese Diskrepanz vernachlässigt.
Nach dem in Abschnitt 2.6.3 erläuterten Verfahren der Extrapolation nach Haller
kann die Doppelbrechung bei einer Temperatur von 0 K, ∆n0, bestimmt werden, die
zur Berechnung des Ordnungsgrades benötigt wird.
Die Messung erfolgt durch Kühlen aus der isotropen Phase in die nematische Phase
in Schritten von 2°C. Die Temperaturbestimmung geschieht über einen Pt100Thermofühler in der Zelle, in der sich auch die Probe befindet. Vor der
Aufzeichnung der Messwerte wird bis zu einer Gleichgewichtseinstellung gewartet.
119
Experimenteller Teil
Eine Detektion eines Messwerts erfolgt, wenn die Phasenverschiebung konstant ist,
frühestens allerdings nach 1200 Sekunden. Ist nach 3600 Sekunden noch keine
Konstanz erreicht – was in den hier durchgeführten Messungen nicht der Fall war wird dennoch der aktuelle Wert aufgezeichnet und zur nächsten Temperatur
übergegangen.
6.6.3. Spannungs-Dehnungs-Messungen
Zur Ermittlung der Spannung in Abhängigkeit der Dehnung bei verschiedenen
Temperaturen wurde die Probe in einer temperierbaren Messzelle mit Pt100Thermofühler zwischen zwei Halterungen angebracht. Die obere Halterung war mit
einer Kraftmessdose versehen. Durch computergesteuertes Verschieben der
Halterungen konnte die Probe gedehnt werden. Die von der Kraftmessdose
gemessene Kraft wurde für jeden Dehnungsschritt detektiert. Zwischen Dehnen der
Probe
und
Detektion
der
Kraft
wurde
1000
Sekunden
gewartet,
damit
Gleichgewichtseinstellung erfolgen konnte.
Aus der Kraft und der Querschnittsfläche wurde die nominale Spannung σnom
berechnet. Zur Ermittlung des elastischen Moduls wird normalerweise die wahre
Spannung σw benötigt. Da sich bei diesen kleinen Dehnungen die Querschnittsfläche
kaum ändert, wird diese vernachlässigt und statt der wahren Spannung die
nominale Spannung benutzt.
Die relative Dehnung λ wurde als Quotient aus absoluter Dehnung L dividiert durch
die Ausgangslänge L0 berechnet (λ=L/L0).
Die Steigung der linearen Regression der Auftragung von nomineller Spannung
gegen relative Dehnung ist der elastische Modul E.
120
Experimenteller Teil
6.6.4. Röntgenmessungen
Röntgenstreuexperimente
werden
mit
monochromatischer
Cu-Kα-Strahlung
(λ=1,5418 Å) durchgeführt. Sie wird von einer Drehanode bei einer Spannung von 40
kV und einem Strom von 100 mA erzeugt. Ein Graphit-Monochromator filtert
unerwünschte Bremsstrahlung und Nebenlinien heraus. Der Kollimator hat einen
Durchmesser von 0,8 mm. Als Detektor wird ein Imageplatesystem verwendet, bei
dem proportional zur Röntgenstrahlung Elektronen-Loch-Paare gebildet werden, die
mit einem He-Ne-Lasers ausgelesen werden können.
Die Belichtungszeit der verstreckten Polymerfasern betrug 1800 Sekunden.
Die
Bilder
wurden
mit
Hilfe
eines
zugehörigen
Imageplate-Programmes
ausgewertet. Es wurde eine radiale Intensitätsverteilung in Abhängigkeit vom
Winkel 2θ erhalten. Der Bereich der Intensitätsmaxima kann mit einer Gaußkurve
gefittet werden. Aus dem Maximum der Gaußkurve kann mit Hilfe der BraggGleichung ein charakteristischer Abstand bestimmt werden. Im Falle der in dieser
Arbeit betrachteten Weitwinkelreflexe handelt es sich um den lateralen MesogenMesogen-Abstand.
n ⋅ λ = 2 ⋅ d ⋅ sin θ
(6.7)
6.6.5. Weitere Geräte, Untersuchungsmethoden und Materialien
6.6.5.1 Differential-Scanning-Kalometrie (DSC)
DSC-Messungen werden mit einem Perkin-Elmer DSC7 bei verschiedenen Heizraten
(9, 16, 25 und 36 K/min) durchgeführt. Zur Bestimmung der Glasübergangstemperatur wurde die Temperatur des halben Übergangs (1/2 ∆Cp) der Aufheizkurven gegen die Heizrate aufgetragen und auf eine Heizrate von 0K extrapoliert.
Die nematisch-isotrope Phasenumwandlungstemperatur wurde als Mittelwert aus
den extrapolierten Werten der Aufheiz- und Abkühlkurven berechnet. Zur
Extrapolation wurden die Maxima der Peaks der jeweiligen Kurve verwendet.
121
Experimenteller Teil
6.6.5.2 Kernresonanzspektroskopie (NMR)
Die NMR-Spektren wurden in einem Bruker ARX-300 Spektrometer aufgenommen.
Als Standard wurde das Protonensignal des CDCl3-Lösungsmittels genommen.
6.6.5.3 Polarisationsmikroskopie und Konoskopie
Die Untersuchungen wurden mit dem Polarisationsmikroskop Leica Ortholux II Pol
BK durchgeführt. Zur Temperierung der Proben wurde der Heiztisch FP80 der Firma
Mettler benutzt. Die Detektion der Lichtintensität erfolgte mit einem in den Heiztisch
integrierten Fotomonitor.
6.6.5.4 FT-IR-Spektroskopie
Die FT-IR-Spektren wurden auf einem Bruker Vector 22 Spektrometer mit der
Auswertsoftware OPUS oder auf einem Nicolet 5DXC mit der Auswertsoftware
Omnic aufgenommen. Die Reaktionslösungen wurden zwischen zwei KBr-Platten
gegeben und in den Strahlengang gebracht.
6.6.5.5 UV-Lampe
Die UV-Vernetzung der Proben wurde mit einer im Institut konstruierten UV-Lampe
durchgeführt. Als Leuchtmittel wurde eine Philips HRLR Lampe mit einer Leistung
von 400 Watt benutzt. Vor Auftreffen der Strahlung auf die Probe wurde Licht im
Infrarotbereich
herausgefiltert.
Die
Lampe
war
ausgestattet
mit
einem
Lüftungspropeller, um einem starken Erhitzen der Probe vorzubeugen. Die
Belichtungszeit war an einer Zeitschaltuhr voreinstellbar.
122
Experimenteller Teil
6.6.5.6 Magnet
Zur Orientierung der Proben wurde der Elektromagnet B-MN C5 der Firma Bruker
verwendet. Das Magnetfeld hatte eine Stärke von ca. 1,7 Tesla.
6.6.5.7 Leitender Zweikomponentenkleber
Zum Befestigen der Elektroden an den Proben zur Untersuchung im elektrischen
Feld diente der silberpartikelhaltige Zweikomponenetenkleber Conductive Epoxy
CW 2400 der Firma Chemtronics.
6.6.5.8 Erzeugung der Wechselspannung
Zur Erzeugung der Wechselspannung wurde der Stromgenerator der Firma
Wavetek, Modell 22, 11 MHz Stabilized Sweep Generator eingesetzt. Es wurde ein
sinusförmiger Wechselstrom erzeugt, dessen Spannung durch den Verstärker der
Firma Krohn-Hite Model 7500 Amplifier modifiziert und regulierbar gemacht
wurde.
6.6.5.9 Dünnschichtchromatographie
Dünnschichtchromatographie
wurde
mit
Kieselgel
F60-beschichteten
Aluminiumplatten der Firma Merck durchgeführt. Die Detektion erfolgte mit UVStrahlung (λ=254 nm) bzw. durch Anfärben mit Jod oder Kaliumpermanganatlösung.
6.6.5.10 Säulenchromatographie
Als stationäre Phase wurde Kieselgel F60 mit einer Korngröße von 0,040-0,063 mm
der Firma Merck verwendet.
123
Experimenteller Teil
6.6.5.11 Katalysator
Als Katalysator wurde der Pt-Katalysator SLM 86003 der Firma Wacker-Chemie
verwendet.
6.7. Gefahren- und Sicherheitshinweise
Chemikalien
Gefahrenklasse
R-Sätze
S-Sätze
Aceton
leichtentzündlich
11
9-16-23.2-33
leichtentzündlich,
Allylbromid
giftig,
11-23/25-34-50
umweltgefährdend
Azodicarbonsäurediisipropylester
Benzophenon
Benzoylchlorid
But-3-en-1-ol
Chloroform (Trichlormethan)
36/37/38
26-37/39
umweltgefährdend
50/53
61
ätzend
34
26-45
mindergiftig
10-36/37/38
---
gesundheitsschädlich,
22-38-40-48-
reizend
20/22
reizend,
umweltgefährdend
Dichlormethan
mindergiftig
giftig, sensibilisierend,
N,N’-Dicyclohexylcarbodiimid
gesundheitsschädlich,
reizend
Diethylether
4-N,N-Dimethylaminopyridin
Dimethylformamid
Essigsäure
Essigsäureethylester
124
36/37/39-45-61
reizend
leichtentzündlich,
Cyclohexan
16-26-
36/37
11-38-50/53-
9-16-33-60-61-
65-67
62
20-40
22-24-37/3841-43
23.2-24/2536/37
26-36/37/39-45
hochentzündlich
12-19
9-16-29-33
giftig, reizend
25-36/38
45
61
53-45
entzündlich, ätzend
10-35
23.2-26-45
leichtentzündlich
11
16-23-29-33
teratogen, reizend,
gesundheitsschädlich
Experimenteller Teil
Ethanol
4-Hydroxybenzoesäuremethylester
Kaliumcarbonat
leichtentzündlich
11
7-16
reizend
36/37/38
26-36
22-36
22-26
gesundheitsschädlich,
reizend
Kaliumhydroxid
ätzend
35
26-37/39-45
Magnesiumsulfat
---
---
---
11-23/25
2-7-16-24
14/15-34
5.2-8-30-43.6
ätzend
35
2-26-37/39
Natriumnitrit
brandfördernd, giftig
8-25
45
Natriumsulfat
---
---
---
leichtentzündlich
11
9-16-29-33
---
---
24-25
Salzsäure
ätzend
36/38
2-28.1
Schwefelsäure 97 %ig
ätzend
35
2-26-30
11-19-36/37
16-29-33
22-43-53
24-37-61
Methanol
Natrium
Natriumhydroxid
Petrolether
Pt-Katalysator SLM 86003
(Fa. Wacker-Chemie, München)
Tetrahydrofuran
Triphenylphosphin
Trideuterochloroform
Toluol
leichtentzündlich,
giftig
leichtentzündlich,
ätzend
leichtentzündlich,
reizend
mindergiftig
carcinogen, giftig
leichtentzündlich,
mindergiftig
20/22-38-4047-48
11-20-47
36/37-53
16-25-29-33-51
Die R-Sätze geben das Risikopotential einer chemischen Substanz an, den S-Sätzen
lassen sich die entsprechenden Sicherheitshinweise entnehmen.
125
Experimenteller Teil
R-Sätze: Hinweise auf besondere Gefahren
R 01
In trockenem Zustand explosionsgefährlich
R 02
Durch Schlag, Reibung, Feuer oder andere Zündquellen explosionsgefährlich
R 03
Durch Schlag, Reibung, Feuer oder andere Zündquellen besonders explosionsgefährlich
R 04
Bildet hochempfindliche explosionsgefährliche Metallverbindungen
R 05
Beim Erwärmen explosionsfähig
R 06
Mit und ohne Luft explosionsfähig
R 07
Kann Brand verursachen
R 08
Feuergefahr bei Berührung mit brennbaren Stoffen
R 09
Feuergefahr bei Mischung mit brennbaren Stoffen
R 10
Entzündlich
R 11
Leichtentzündlich
R 12
Hochentzündlich
R 14
Reagiert heftig mit Wasser
R 15
Reagiert mit Wasser unter Bildung hochentzündlicher Gase
R 16
Explosionsgefährlich in Mischung mit brandfördernden Stoffen
R 17
Selbstentzündlich an der Luft
R 18
Bei Gebrauch Bildung explosionsfähiger/leichtentzündlicher Dampf-Luftgemische möglich
R 19
Kann explosionsfähige Peroxide bilden
R 20
Gesundheitsschädlich beim Einatmen
R 21
Gesundheitsschädlich bei Berührung mit Haut
R 22
Gesundheitsschädlich beim Verschlucken
R 23
Giftig beim Einatmen
R 24
Giftig bei Berührung mit Haut
R 25
Giftig beim Verschlucken
R 26
Sehr giftig beim Einatmen
R 27
126
Sehr giftig bei Berührung mit Haut
Experimenteller Teil
R 28
Sehr giftig beim Verschlucken
R 29
Entwickelt bei Berührung mit Wasser giftige Gase
R 30
Kann bei Gebrauch leichtentzündlich werden
R 31
Entwickelt bei Berührung mit Säure giftige Gase
R 32
Entwickelt bei Berührung mit Säure sehr giftige Gase
R 33
Gefahr kumulativer Wirkungen
R 34
Verursacht Verätzungen
R 35
Verursacht schwere Verätzungen
R 36
Reizt die Augen
R 37
Reizt die Atmungsorgane
R 38
Reizt die Haut
R 39
Ernste Gefahr irreversiblen Schadens
R 40
Irreversibler Schaden möglich
R 41
Gefahr ernster Augenschäden
R 42
Sensibilisierung durch Einatmen möglich
R 43
Sensibilisierung durch Hautkontakt möglich
R 44
Explosionsgefahr bei Erhitzen unter Einschluß
R 45
Kann Krebs erzeugen
R 46
Kann vererbbare Schäden verursachen
R 48
Gefahr ernster Gesundheitsschäden bei längerer Exposition
R 49
Kann Krebs erzeugen beim Einatmen
R 50
Sehr giftig für Wasserorganismen
R 52
Schädlich für Wasserorganismen
R 53
Kann in Gewässern längerfristig schädliche Wirkungen haben
R 54/55/56 Giftig für Pflanzen/Tiere/Bodenorganismen
R 57
Giftig für Bienen
R 58
Kann längerfristig schädliche Wirkungen auf die Umwelt haben
R 59
Gefährlich für die Ozonschicht
R 60
Kann die Fortpflanzungsfähigkeit beeinträchtigen
127
Experimenteller Teil
R 61
Kann das Kind im Mutterleib schädigen
R 62
Kann möglicherweise die Fortpflanzungsfähigkeit beeinträchtigen
R 63
Kann das Kind im Mutterleib möglicherweise schädigen
R 64
Kann Säuglinge über die Muttermilch schädigen
S-Sätze: Sicherheitsratschläge
S 01
Unter Verschluß aufbewahren
S 02
Darf nicht in die Hände von Kindern gelangen
S 03
Kühl aufbewahren
S 04
Von Wohnplätzen fernhalten
S 05
Unter ..(geeignete Flüssigkeit).. aufbewahren
S 06
Unter ..(inertes Gas).. aufbewahren
S 07
Behälter dicht geschlossen halten
S 08
Behälter trocken halten
S 09
Behälter an einem gut gelüfteten Ort aufbewahren
S 12
Behälter nicht gasdicht verschließen
S 13
Von Nahrungsmitteln, Getränken und Futtermitteln fernhalten
S 14
Von ..(inkompatible Substanzen).. fernhalten
S 15
Vor Hitze schützen
S 16
Von Zündquellen fernhalten - Nicht rauchen
S 17
Von brennbaren Stoffen fernhalten
S 18
Behälter mit Vorsicht öffnen und handhaben
S 20
Bei der Arbeit nicht essen und trinken
S 21
Bei der Arbeit nicht rauchen
S 22
Staub nicht einatmen
S 23
Gas/Rauch/Dampf/Aerosol nicht einatmen
S 24
Berührung mit der Haut vermeiden
S 25
Berührung mit den Augen vermeiden
128
Experimenteller Teil
S 26
Bei Berührung mit den Augen gründlich mit Wasser ausspülen und Arzt
konsultieren
S 27
Beschmutzte, getränkte Kleidung sofort ausziehen
S 28
Bei Berührung mit der Haut sofort Abwaschen mit viel...
S 29
Nicht in die Kanalisation gelangen lassen
S 30
Niemals Wasser hinzugießen
S 33
Maßnahmen gegen elektrostatische Aufladungen treffen
S 35
Abfälle und Behälter müssen in gesicherter Weise beseitigt werden
S 36
Bei der Arbeit geeignete Schutzkleidung tragen
S 37
Geeignete Schutzhandschuhe tragen
S 38
Bei unzureichender Belüftung Atemschutzgerät tragen
S 39
Schutzbrille/Gesichtsschutz tragen
S 40
Fußboden und verunreinigte Gegenstände mit ... reinigen
S 41
Explosions- und Brandgase nicht einatmen
S 42
Bei Räuchern/Versprühen geeignetes Atemschutzgerät anlegen
S 43
Zum Löschen ... verwenden (wenn Wasser die Gefahr erhöht, anfügen: Kein
Wasser verwenden)
S 45
Bei Unfall oder Unwohlsein sofort Arzt hinzuziehen (wenn möglich dieses
Etikett vorzeigen)
S 46
Bei Verschlucken sofort ärztlichen Rat einholen und Verpackung oder Etikett
vorzeigen
S 47
Nicht bei Temperaturen über ... °C aufbewahren
S 48
Feucht halten mit ...
S 49
Nur im Originalbehälter aufbewahren
S 50
Nicht mischen mit ...
S 51
Nur in gut belüfteten Bereichen verwenden
S 52
Nicht großflächig für Wohn- und Arbeitsräume verwenden
S 53
Exposition vermeiden - vor Gebrauch besondere Anweisungen einholen
S 56
Diesen Stoff und seinen Behälter der Problemabfallentsorgung zuführen
129
Experimenteller Teil
S 57
Zur Vermeidung einer Kontamination der Umwelt geeigneten Behälter
verwenden
S 59
Information zur Wiederverwendung/Wiederverwertung beim Hersteller/
Lieferanten erfragen
S 60
Dieser Stoff und sein Behälter sind als gefährlicher Abfall zu entsorgen
S 61
Freisetzung in der Umwelt vermeiden. Besondere Anweisungen einholen/
Sicherheitsdatenblatt zu Rate ziehen
S 62
Bei Verschlucken kein Erbrechen herbeiführen. Sofort ärztlichen Rat einholen
und Verpackung oder dieses Etikett vorzeigen
130
7. Literatur
[1]
De Gennes, P. G. Physics Letters A 1969, A 30, (8), 454-&.
[2]
De Gennes, P. G. Molecular Crystals and Liquid Crystals 1971, 12, (3), 193-&.
[3]
De Gennes, P. G. Comptes Rendus Hebdomadaires Des Seances De L Academie Des
Sciences Serie B 1975, 281, (5-8), 101-103.
[4]
De Gennes, P. G., In Liquid Crystals of One- and Two-Dimensional Order,
Helfrich, W.; Heppke, G., Eds. Springer: Berlin, 1980.
[5]
De Gennes, P. G.; Probst, J., The Physics of Liquid Crystals. 2nd ed.; Clarendon
Press: Oxford, 1993.
[6]
Landau, L. Phys. Z. Sowjet. 1937, 11, 26.
[7]
Greve, A.; Finkelmann, H. Macromolecular Chemistry and Physics 2001, 202, (14),
2926-2946.
[8]
Ohm, H. G.; Kirste, R. G.; Oberthur, R. C. Makromolekulare Chemie-
Macromolecular Chemistry and Physics 1988, 189, (6), 1387-1405.
[9]
Kirste, R. G.; Kruse, W. A.; Ibel, K. Polymer 1975, 16, (2), 120-124.
[10]
Noirez, L.; Keller, P.; Cotton, J. P. Liquid Crystals 1995, 18, (1), 129-148.
[11]
Lecommandoux, S.; Noirez, L.; Achard, M. F.; Brulet, A.; Cotton, J. P.;
Hardouin, F. Physica B 1997, 234, 250-251.
[12]
Warner, M.; Terentjev, E. M. Progress in Polymer Science 1996, 21, (5), 853-891.
[13]
Finkelmann, H.; Kock, H. J.; Gleim, W.; Rehage, G. Makromolekulare Chemie-
Rapid Communications 1984, 5, (5), 287-293.
[14]
Finkelmann, H.; Gleim, W.; Hammerschmidt, K.; Schatzle, J. Makromolekulare
Chemie-Macromolecular Symposia 1989, 26, 67-67.
[15]
Hammerschmidt, K.; Finkelmann, H. Makromolekulare Chemie-Macromolecular
Chemistry and Physics 1989, 190, (5), 1089-1101.
131
Literatur
[16]
Gleim, W., Finkelmann, H., Side Chain Liquid Crystal Polymers. Blackie and Son
Ltd.: Glasgow, 1989.
[17]
Schatzle, J.; Finkelmann, H. Molecular Crystals and Liquid Crystals 1987, 142, (14), 85-100.
[18]
Mitchell, G. R.; Coulter, M.; Davis, F. J.; Guo, W. Journal De Physique Ii 1992, 2,
(5), 1121-1132.
[19]
Guo, W.; Davis, F. J.; Mitchell, G. R. Polymer 1994, 35, (14), 2952-2961.
[20]
Strobl, G., The Physics of Polymers. 2nd ed.; Springer: Berlin, Heidelberg, 1997.
[21]
Hiemenz, P. C., Polymer Chemistry, The Basic Concepts. Marcel Dekker inc.: New
York, Basel, 1984.
[22]
Kuhn, W. G., F. Kolloid Zeitschrift 1942, 101, 248.
[23]
Erman, B.; Flory, P. J. Macromolecules 1983, 16, (10), 1601-1606.
[24]
Erman, B.; Flory, P. J. Macromolecules 1983, 16, (10), 1607-1613.
[25]
Galiatsatos, V. Macromolecules 1990, 23, (16), 3817-3821.
[26]
Rennar, N. Berichte Der Bunsen-Gesellschaft-Physical Chemistry Chemical Physics
1998, 102, (11), 1665-1671.
[27]
Boeffel, C.; Spiess, H. W.; Hisgen, B.; Ringsdorf, H.; Ohm, H.; Kirste, R. G.
Makromolekulare Chemie-Rapid Communications 1986, 7, (12), 777-783.
[28]
Wang, X. J.; Warner, M. Journal of Physics a-Mathematical and General 1987, 20,
(3), 713-731.
[29]
Warner, M., Side Chain Liquid Crystal Polymers. Blackie and Son Ltd.: Glasgow,
1989.
[30]
Kupfer, J.; Finkelmann, H. Makromolekulare Chemie-Rapid Communications 1991,
12, (12), 717-726.
[31]
Komp, A.; Ruhe, J.; Finkelmann, H. Macromolecular Rapid Communications 2005,
26, (10), 813-818.
[32]
Küpfer, J.; Finkelmann, H. Makromolekulare Chemie-Rapid Communications 1991,
12, (12), 717-726.
[33]
132
Hermans, P. H. P., P. Kolloid Zeitschrift 1939, 88, 65.
[34]
Maier, W.; Saupe, A. Zeitschrift Fur Naturforschung Part a-Astrophysik Physik
Und Physikalische Chemie 1958, 13, (7), 564-566.
[35]
Saupe, A.; Maier, W. Zeitschrift Fur Naturforschung Part a-Astrophysik Physik
Und Physikalische Chemie 1961, 16, (8), 816-824.
[36]
Mitchell, G. R.; Lovell, R. Acta Crystallographica Section A 1981, 37, (Mar), 189196.
[37]
Mitchell, G. R.; Windle, A., Orientation in Liquid Crystal Polymers. In
Developments in Crystalline Polymers-2, Basset, D. C., Ed. Elsevier Applied
Science: London, New York, 1988.
[38]
Haller, I. Progress in Solid-State Chemistry 1975, 10, 103.
[39]
Degennes, P. G. Physics Letters A 1969, A 30, (8), 454-&.
[40]
Degennes, P. G. Molecular Crystals and Liquid Crystals 1971, 12, (3), 193-&.
[41]
Chatelain, P. Bull. Soc. Fr. Minér. 1955, 78, 262.
[42]
Vuks, M. F. Optics and Spectroscopy-Ussr 1966, 21, (6), 383-&.
[43]
Chandras.S; Krishnam.D; Madhusud.Nv. Molecular Crystals and Liquid Crystals
1969, 8, 45-&.
[44]
Haller, I.; Huggins, H. A.; Lilienth.Hr; Mcguire, T. R. Journal of Physical
Chemistry 1973, 77, (7), 950-954.
[45]
Margenau, H. M., G. M., The Mathematics of Physics and Chemistry. 2nd ed.; R.
E. Krieger Pub. Co: Princeton, 1956.
[46]
Degennes, P. G. Comptes Rendus Hebdomadaires Des Seances De L Academie Des
Sciences Serie B 1975, 281, (5-8), 101-103.
[47]
Kaufhold, W.; Finkelmann, H.; Brand, H. R. Makromolekulare Chemie-
Macromolecular Chemistry and Physics 1991, 192, (11), 2555-2579.
[48]
Gleim, W.; Finkelmann, H. Makromolekulare Chemie-Macromolecular Chemistry
and Physics 1987, 188, (6), 1489-1500.
[49]
Schatzle,
J.;
Kaufhold,
W.;
Finkelmann,
H.
Makromolekulare
Chemie-
Macromolecular Chemistry and Physics 1989, 190, (12), 3269-3284.
[50]
Kaufhold, W. Dissertation. Universität Freiburg, 1991.
133
Literatur
[51]
Disch, S.; Schmidt, C.; Finkelmann, H. Macromolecular Rapid Communications
1994, 15, (4), 303-310.
[52]
Sheng, P. Physical Review Letters 1976, 37, (16), 1059-1062.
[53]
Sheng, P. Physical Review A 1982, 26, (3), 1610-1617.
[54]
Pelzl, G., Thermodynamic Behavior and Physical Properties of Thermotropic
Liquid Crystals. In Liquid Crystals, Stegemeyer, H., Ed. Springer: New York,
1994.
[55]
Greve, A. Dissertation. Universität Freiburg, 2000.
[56]
Kniesel, S. Dissertation. Universität Freiburg, 2005.
[57]
Lim, K. C.; Ho, J. T. Molecular Crystals and Liquid Crystals 1978, 47, (3-4), 173177.
134
Mein Dank gilt...
... Herrn Prof. Dr. Heino Finkelmann für die Vergabe des interessanten Themas, die
ständige Hilfs- und Diskussionsbereitschaft und das überaus angenehme
Arbeitsklima.
... Herrn Prof. Dr. Eckhard Bartsch für die freundliche Übernahme des Korreferats.
... Carina Asal, Christina Sprich, Katharina Dixa, Elke Stibal-Fischer und Heidi
Wisser für die Ausführung zahlreicher Synthesen und die Hilfe bei Laborfragen.
... Carola Sturm und Florian Müller für die Durchführung der DSC-Messungen.
... Alfred Hasenhindl und Dr. Michael Kowalski für die NMR-Messungen.
... Alexander Rossel, Bernd Machutta, Erik Hügle und der ganzen Werkstatt für die
schnelle Erledigung von Werkstattaufträgen.
... Felicitas Brömmel und Frank Zander für das eifrige Korrekturlesen dieser Arbeit.
... Ansgar Komp und Alex Potdevin für die Hilfe und das „Handauflegen“ bei
Computerproblemen.
... Allen aktuellen und ehemaligen Mitarbeitern des Arbeitskreises Finkelmann für
die tolle Zeit. Es hat Spaß gemacht!
... Uwe für die vielen Dinge, die er für mich getan hat, und die schöne Zeit in
Freiburg.
... Andreas nicht nur (!) für die gemeinsamen Laufrunden.
... Meinen Eltern und meiner ganzen Familie, die mich immer in jeglicher Hinsicht
unterstützen und an mich glauben.