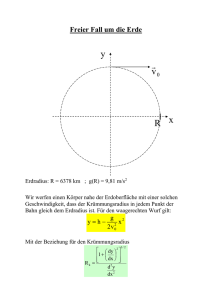
Die geometrische Entfernungsleiter

DIE GEOMETRISCHE ENTFERNUNGSLEITER
Vom Erdradius über die Astronomische Einheit
zur Entfernung naher Sterne
Diplomarbeit
in der Studienrichtung
Lehramtsstudium Physik - Mathematik
zur Erlangung des akademischen Grades
MAGISTER
DER
NATURWISSENSCHAFTEN
eingereicht an der
FAKULTÄT
MATHEMATIK, INFORMATIK UND PHYSIK
DER U NIVERSITÄT I NNSBRUCK
FÜR
von
ARMIN LÄSSER
BETREUER:
UNIV.-PROF. MAG. DR. WALTER SAURER,
INSTITUT FÜR ASTRO - UND TEILCHENPHYSIK
INNSBRUCK, OKTOBER 2008
Für meine Großeltern und Eltern
i
Danksagung
Dank gebührt in erster Linie meinen Eltern für ihre großzügige und bedingungslose
Unterstützung.
Weiters bedanke ich mich bei meinen Freunden, die mir während des Studiums zum
nötigen Ausgleich verhalfen.
Besonders hervorheben möchte ich dabei meinen Kommilitonen Robert, ohne den man
mich in den letzten Jahren selten auf der Universität angetroffen hat, und meine Freundin
Nini, die meinen gelegentlichen Unmut aushielt und mich immer wieder aufbaute.
Meinen speziellen Dank möchte ich Dr. Vroni aussprechen, die diese Diplomarbeit
„fachfraulich“ korrigierte.
Nicht zuletzt schulde ich Herrn Univ.-Prof. Mag. Dr. Walter Saurer großen Dank für die
kompetente Betreuung. Er hatte stets Zeit für meine Anliegen und stand mir mit wertvollem
Rat zur Seite.
ii
Abstract
Entfernungen messen, ohne sie zurücklegen zu müssen...
Dieses Anliegen gelang hinsichtlich des Erdradius schon vor über 2 000 Jahren, für den
Abstand zur Sonne und den Sternen jedoch erst in den letzten Jahrhunderten. Angefangen
mit der Methode von Eratosthenes zur Bestimmung des Erdumfangs gelangt der Leser
über die Verfahren von Aristarch, Hipparch, Kepler und vielen anderen, die sich dabei
astronomische Phänomene wie Venustransite, Sonnen- und Mondfinsternisse zu Nutze
machten, bis zur Messung des Abstandes naher Sterne mittels Sternparallaxe.
Was die meisten Vorgehensweisen gemeinsam haben, ist die geometrische Idee dahinter:
Durch Beobachtung des Zielobjektes von zwei verschiedenen Orten aus, von denen die
dazwischenliegende Distanz bekannt ist, kann mittels Trigonometrie auf seine Entfernung
geschlossen werden. Aus dieser Idee entwickelt sich der Begriff der Parallaxe, der besonders
im zweiten und dritten Kapitel eine wichtige Rolle spielt.
Aufgebaut sind die Kapitel nach den einzelnen Sprossen der Entfernungsleiter. Erst nach
Bewältigung der vorhergehenden Sprosse kann die nächste erklommen werden – nur wenn
man die Länge des Erdradius hinreichend genau weiß, kann man die absolute Distanz zur
Sonne angeben; und erst wenn diese bekannt ist, kommt man auf die Entfernung naher
Sterne.
iii
Inhaltsverzeichnis
Danksagung
ii
Abstract
iii
Inhaltsverzeichnis
iv
0. Einführung
1
0.1. Raumwahrnehmung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
0.2. Längeneinheiten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
0.3. Messmethoden . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
0.4. Messunsicherheit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
1. Erste Sprosse: Die Erde
10
1.1. Antike . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
10
1.1.1. Eratosthenes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13
1.1.2. Poseidonios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
17
1.2. Mittelalter . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
19
1.3. Neuzeit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
20
1.4. Heute . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
23
2. Zweite Sprosse: Das Sonnensystem
25
2.1. Antike . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
28
2.1.1. Aristarch . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
28
2.1.2. Hipparch . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
33
2.1.3. Poseidonios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
41
2.1.4. Ptolemäus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
42
2.2. Mittelalter . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
49
2.3. Neuzeit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
50
2.3.1. Kopernikus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
50
iv
2.3.2. Tycho und Kepler . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
58
2.3.3. Die Erfindung des Teleskops . . . . . . . . . . . . . . . . . . . . . . . . .
65
2.3.4. Venustransite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
68
2.3.5. Weitere Methoden . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
81
2.4. Heute . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
83
3. Dritte Sprosse: Nahe Sterne
84
3.1. Abschätzungen bis ins 19. Jahrhundert . . . . . . . . . . . . . . . . . . . . . . .
84
3.2. Nebenprodukte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
88
3.2.1. Die Eigenbewegung von Sternen . . . . . . . . . . . . . . . . . . . . . .
88
3.2.2. Die Aberration des Lichts und die Nutation der Erdachse . . . . . . .
88
3.2.3. Doppelsterne . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
89
3.3. Die ersten gemessenen Sternparallaxen . . . . . . . . . . . . . . . . . . . . . .
90
3.4. Heute . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
93
A. Didaktische Aspekte
96
A.1. Legitimation von astronomischen Entfernungsbestimmungen . . . . . . . . .
96
A.2. Genetischer Unterricht . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
97
A.3. Einstiege und Methoden . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
98
A.4. Fächerübergreifende Inhalte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102
A.5. Arbeitsblatt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102
B. Originaltexte
105
B.1. Aristarch . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105
B.2. Hipparch . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 107
B.3. Ptolemäus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108
B.4. Newton . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109
Abbildungsverzeichnis
110
Tabellenverzeichnis
112
Literaturverzeichnis
113
Curriculum Vitae
119
Eidesstattliche Erklärung
120
v
0. Einführung
0.1. Raumwahrnehmung
Der Mensch verfügt über eine Raumwahrnehmung, also das Sehen räumlicher Tiefe. Diese
Fähigkeit erlaubt uns, Entfernungen zu Objekten einzuschätzen und somit beispielsweise
die richtige Entscheidung zu treffen, ob wir einen Gegenstand mit der Hand erreichen
können oder nicht. Unser Gehirn benötigt dazu wenig Anstrengung und kein Maßband.
Welche Anhaltspunkte ermöglichen uns, vom zweidimensionalen Abbild auf unserer
Netzhaut auf eine dreidimensionale Umgebung zu schließen?1
Abb. 0.1.: Räumliche Tiefe in zweidimensionalen Bildern
Monokulare („einäugige“) Raumwahrnehmung:
• Relative Größe: Durch die Größe des Bildes eines Gegenstands auf unserer Netzhaut
und dem Wissen um seine wahre Größe können wir auf dessen Entfernung schließen,
1
Für die nachfolgende Aufzählung vgl. GOLDSTEIN, E. Bruce: Wahrnehmungspsychologie. Spektrum, 2002,
S. 225ff.
1
0.1. RAUMWAHRNEHMUNG
Einführung
weil sich der Winkel, unter dem wir das Objekt sehen, mit der Entfernung verkleinert.
Z. B. ist das hintere Auto in Abbildung 0.1 viel kleiner abgebildet als das vordere.
• Verdeckung: Verdeckte Objekte werden als weiter hinten wahrgenommen.
• Perspektive: Parallele Linien scheinen zu konvergieren bzw. sich am Horizont in
einem Punkt zu treffen. Anstatt anzunehmen, dass sich die Linien wirklich näher
kommen, haben wir gelernt, das Abbild räumlich zu interpretieren. Ein Beispiel dafür
sind die Straßenmarkierungen in Abbildung 0.1.
• Bewegungsparallaxe2 : Für einen bewegten Betrachter ziehen nahe Objekte schneller vorbei
als weiter entfernte (s. Abb. 0.2). Dieser Effekt ist auch schon bei leichtem Bewegen des
Kopfes bemerkbar.
• Atmosphärische Perspektive: Durch Streuung
des Lichts an verschiedensten Teilchen in der
Luft erscheinen weiter entfernte Punkte unschärfer, heller und weniger kontrastreich, wie
z. B. die Berge in Abbildung 0.1.
• Relative Höhe zum Horizont: Objekte, die im
Blickfeld in Horizontnähe liegen, werden als
weiter entfernt wahrgenommen als Objekte,
die wir darüber oder darunter sehen, weil sich Abb. 0.2.: Das Bild des näher gelegein unserer Erfahrung der Horizont weit weg befindet (vgl. Perspektive & s. Abb. 0.3)). Wenn
nun zwei Objekte gleich groß auf der Netzhaut
abgebildet sind, glauben wir, dass jenes, das
nen Punktes A verändert bei
Bewegung des Beobachters
seine Position auf der Netzhaut mehr als das Bild von
Punkt B.
wir näher am Horizont sehen, real größer sein
muss, weil wir es ja für weiter entfernt halten (vgl. Relative Größe). Auf dieser Sinnestäuschung beruht u. a. die so genannte Mondtäuschung: Obwohl wir den Mond
knapp über dem Horizont unter demselben Winkel sehen wie bei seinem Höchststand,
erscheint er uns beim Auf- oder Untergehen am größten. Mit anderen Worten: Wir
nehmen ein abgeflachtes Firmament statt einer Halbkugelschale wahr.
2
gr. παράλλαξις (parállaxis) „Veränderung, Abweichung“
2
0.1. RAUMWAHRNEHMUNG
Einführung
Horizont
Abb. 0.3.: Die Objekte nahe am Horizont erscheinen größer, weil sie von unserem Gehirn als weit
entfernt interpretiert werden. Die gestrichelten Linien stellen die gewohnte Dimensionierung dar, der zufolge ein Quader und ein Kreis derselben tatsächlichen Größe wie die der
„vorderen“ zwei Objekte nur sehr klein gesehen werden dürfte. Deshalb halten wir den
Quader und den Kreis nahe am Horizont für größer.
• Scheinbare Helligkeit: Im Dunkeln können wir die Entfernung zu einer Lichtquelle
einschätzen, wenn uns deren Leuchtkraft bekannt ist, z. B. Autoscheinwerfer, Hausbeleuchtung. Allerdings können wir nicht zwischen einer schwachen näheren und
einer starken weiter entfernten Lichtquelle unterscheiden.
• Schatten: Die Distanz zwischen Schatten und Gegenstand gibt Aufschluss darüber,
wie weit der Gegenstand vom Untergrund entfernt ist (s. Abb. 0.4).
• Akkommodation3 : Der Ziliarmuskel verändert die Brennweite der Augenlinse so,
dass Gegenstände unterschiedlicher Entfernung auf der Netzebene scharf dargestellt
werden.
Binokulare („zweiäugige“) Raumwahrnehmung:
• Konvergenz: Bei der Betrachtung naher Objekte konvergieren die Augen, d. h. man
schielt. Bei weiter entfernten stehen sie parallel.
Diese zwei Effekte nennt man okulomotorisch („das Auge bewegend“).
• Parallaxe oder Querdisparität: Durch den Abstand zwischen unseren Augen entstehen
unterschiedliche Netzhautbilder. Je weiter ein Gegenstand entfernt ist, desto geringer
ist der Unterschied zwischen den beiden Abbildungen.
3
lat. accomodare „anpassen“
3
0.2. LÄNGENEINHEITEN
Einführung
Abb. 0.4.: Obwohl die weißen Rechtecke gleich groß abgebildet sind, erscheinen sie uns unterschiedlich weit vom Hintergrund entfernt.
Keine dieser Methoden ermöglicht uns jedoch, die Entfernung zu Himmelsobjekten
einzuschätzen, weil sie zu weit weg sind und uns Erfahrungswerte zu ihrer wahren Größe
und Leuchtkraft fehlen. Außerdem beruhen diese Messprinzipien großteils auf Erlerntem
oder psychologischen Effekten, sind daher fehleranfällig und eignen sich nicht zur objektiven Entfernungsmessung. Dennoch werden wir später auf einige dieser Prinzipien
zurückkommen, insbesondere der Parallaxenbegriff wird eine große Bedeutung bekommen.
0.2. Längeneinheiten
Durch die Raumwahrnehmung haben wir eine intuitive Vorstellung von Entfernungen in
unserer direkten Umwelt. Um quantitativ über Abstände sprechen zu können, benötigen
wir jedoch Standardmaße. Im Laufe der Zeit entwickelte die Menschheit eine Vielzahl solcher Standards. Die älteste Maßeinheit stammt wahrscheinlich aus dem Neolithikum (um
5000 v. Chr.) und entspricht ca. 83 cm. Sie wurde an Grundrissen von Häusern im Rheinland statistisch nachgewiesen. Der schottische Ingenieur Prof. Alexander Thom entdeckte
dieselbe Maßeinheit schon 1955 an Megalithbauten aus dem 3. Jtsd. v. Chr. in England,
Schottland und der Bretagne. Daher erhielt sie von ihm den Namen „Megalithisches Yard“.
Ob es tatsächlich verwendet wurde, ist jedoch nach wie vor umstritten, da es sich, so die
Kritiker, nur um einen Mittelwert aus Messwerten handelt.
Die so genannte Nippur-Elle, ein Stab aus einer Kupferlegierung, der in einem mesopotamischen Tempel in Nippur gefunden wurde, gilt als der älteste dingliche Maßstab. Sie ist
4
0.2. LÄNGENEINHEITEN
Einführung
knapp über einen halben Meter lang und wird auf 2800 v. Chr. datiert. Diese Einheit war
im Orient weit verbreitet und steht mit dem Megalithischen Yard genau im Verhältnis 5 zu
8, weshalb manche Wissenschaftler einen Zusammenhang sehen4 .
Bis heute haben sich insbesondere in den USA viele Längeneinheiten gehalten, die
sich, wie auch die Elle, auf menschliche Körperteile beziehen. Der Zoll (engl. Inch, 1 in =
2,54 cm) entspricht einer Daumenbreite und ist heute als ein Zwölftel des englischen Fuß
(engl. Foot, 1 ft = 30,48 cm) definiert. Drei Feet ergeben das Yard (1 yd = 91,44 cm), das
sich von der Schrittweite ableitet. Eine britische Landmeile setzt sich aus 1 760 Yards
zusammen (1 mi = 1,61 km). Der Begriff Meile leitet sich jedoch von der römischen Meile
ab, die mille passus hieß, was übersetzt 1 000 Doppelschritte bedeutet. Neben der Definition
dieser angloamerikanischen Maßeinheiten gab es jedoch viele verschiedene Standards, die
häufig auf die Körpermaße der jeweiligen Herrscher abgestimmt waren und sich deshalb
auch oft änderten.
Da die Fallbeschleunigung auf der Erde als konstant angesehen wurde, schlug Christiaan
Huygens 1664 das Sekundenpendel als Standardmaß vor – also die Länge jenes Pendels,
das eine halbe Periodendauer von einer Sekunde hat. Eine Sekunde wiederum war als
86 400ster (= 24 · 60 · 60) Teil eines mittleren Sonnentages definiert. Im Schwerefeld von
Europa hätte ein solches Pendel die Länge von 0,994 Meter und käme damit der heutigen
Definition eines Meters ziemlich nahe.
Der Begriff Meter5 für diese Längeneinheit wurde erstmals von Tito Livio Burattini
in seinem 1675 erschienen Werk Misura Universale verwendet. Darin bezeichnete er die
Länge des Sekundenpendels als „Metro Cattolico“ („katholischer6 Meter“). Der französische
Astronom Gabriel Mouton schlug bereits 1670 vor, die Bogenminute eines Erdmeridiangrads
als Naturmaß zu verwenden und sie nach dem Dezimalsystem zu unterteilen, konnte sich
aber nicht durchsetzen.7 Aufgrund der geistigen Entwicklung während des Zeitalters
der Aufklärung und der Zunahme des internationalen Handels und wissenschaftlichen
Austauschs wurde die Schaffung von einheitlichen, rein rational erklärbaren Maßen immer
unumgänglicher. Es dauerte jedoch bis zum Jahre 1795, dass in dem von der Revolution
geprägten Frankreich der zehnmillionste Teil der Entfernung vom Äquator zum Nordpol
als Grundeinheit für alle Vermessungen gesetzlich festgelegt und Meter genannt wird.
Vgl. ROTTLÄNDER, Rolf: Vormetrische Längenmaße. vormetrische-laengeneinheiten.de – Zugriff
am 24.10.2007.
5
gr. µέτρoν (métron) „Maß“
6
gr. καθoλικóς (katholikós) „das Ganze betreffend, allgemeingültig“
7
Vgl. HAUSTEIN, Heinz-Dieter: Weltchronik des Messens. de Gruyter, 2001, S. 183f.
4
5
0.2. LÄNGENEINHEITEN
Einführung
Tatsächlich legte man dem Urmeter nur die
Vermessung des Meridianbogens durch Paris
von Dünkirchen nach Barcelona zugrunde (s.
Abb. 0.5)8 . Ein Prototyp dieses Meters wurde
vorerst aus Messing, dann aus Platin und 1889
schließlich aus einer Platin-Iridium-Legierung
gefertigt. Im 19. Jahrhundert führte man das
metrische System in den meisten europäischen
Ländern ein, 1871 beispielsweise in Österreich.9
Außer in Myanmar, Liberia und den USA ist es
mittlerweile überall gesetzlich verankert, wobei
es jedoch in der Praxis von den beiden erstgenannten verwendet wird.
Um eine höhere Präzision zu erlangen, löste 1960 die Definition mithilfe der Wellenlänge
der ausgesandten Strahlung von Kryptonatomen bei einem bestimmten Übergang das Urmeter ab. Da die Zeit genauer als Strecken gemessen werden kann, ist der Meter mittlerweile
als die Strecke definiert, die das Licht im Vakuum in
1
299 792 458
Abb. 0.5.: Vermessung der Strecke
Dünkirchen – Barcelona
Sekunden zurücklegt, wobei die
Sekunde seit 1967 aus atomaren Messungen abgeleitet wird.10
Es sei noch erwähnt, dass den Vermessern der Strecke Dünkirchen – Barcelona kleine
Fehler unterliefen. „Heute wissen wir, dass die gemittelte Entfernung zwischen Nordpol
und Äquator rund 10 002 000 Meter beträgt, was bedeutet, dass der Meter ungefähr 0,2
Millimeter (die Dicke von zwei Blatt Papier) zu kurz ist. [...]“ Daher „ist es vielleicht
nicht mehr ganz so überraschend, dass die Amerikaner dem metrischen System mit einem
gewissen Argwohn begegnen.“11
Für astronomische Größenordnungen haben sich aus praktischen Gründen, auf die in
den jeweiligen Kapiteln eingegangen wird, jedoch weitgehend andere Einheiten wie die
Astronomische Einheit, das Parsec oder das Lichtjahr durchgesetzt. Aufgrund der enormen
8
Vgl. HAEDER, Walter: Von der Königlichen Elle zum Meter. Beuth, 1973, S. 49.
Vgl. HAUSTEIN: Weltchronik des Messens, S. 269.
10
Vgl. PHYSIKALISCH-TECHNISCHE BUNDESANSTALT: Die PTB als Hüterin der Einheiten.
www.ptb.de/de/wegweiser/einheiten – Zugriff am 05.11.2007.
11
ALDER, Ken: Der Meter misst keinen Meter! NZZ Folio, Die Zeitschrift der Neuen Zürcher Zeitung – Thema:
Normen, 2005, Nr. 02.
9
6
0.3. MESSMETHODEN
Einführung
Distanzen im Weltall würde eine Angabe in Metern auch kaum der Vorstellung dienen. Die
Entfernung von unserer Sonne zum nächsten Stern (Proxima Centauri) beträgt z. B. rund
40 Billionen Kilometer, also 4 · 1016 Meter.
0.3. Messmethoden
Wenn man Entfernungen nicht mehr direkt, also z. B. mittels Maßbandes, messen kann,
muss man sie indirekt bestimmen, d. h. es wird nicht die Entfernung selbst, sondern eine
davon abhängige Größe gemessen. Bei Fahrzeugen etwa kann man durch Abzählen der
Umdrehungen und Abmessen des Radumfangs die zurückgelegte Entfernung berechnen.
Mit Hilfe der Inertialnavigation – auch Trägheitsnavigation – werden beispielsweise bei
Flugzeugen, U-Booten, aber auch in der Raumfahrt zurückgelegte Entfernungen durch
zweifaches Integrieren von gemessenen Beschleunigungen über die Zeit bestimmt.
Distanzen zu ermitteln, ohne diese zurücklegen zu müssen, gelingt z. B. durch die Laufzeitmessung eines ausgesandten und vom Messobjekt reflektierten elektromagnetischen
oder akustischen Signals, angewandt etwa bei Radaranlagen, Echoloten und von Fledermäusen; oder mit Triangulation, also dem Anpeilen des gesuchten Messpunktes von
mindestens zwei verschiedenen Standpunkten mit bekanntem Abstand mit Hilfe eines
Winkelmessers und anschließendem Errechnen der anderen Dreieckseiten. Letztere Methode hatte schon Thales von Milet im sechsten vorchristlichen Jahrhundert verwendet,
um die Entfernung eines Schiffes von der Küste zu bestimmen. Eine weitere indirekte
Messmethode wird Thales zugeschrieben: Er soll die Schattenlänge der Cheops-Pyramide
mit der Schattenlänge eines Stabes bekannter Größe verglichen und daraus ihre Höhe
errechnet haben (s. Abb. 0.6).12
Da die Raumfahrt erst durch technische Entwicklungen im letzten Jahrhundert ermöglicht wurde und Raumsonden bis jetzt gerade einmal die Grenze unseres Sonnensystems
erreichen, mussten zur Bestimmung von astronomischen Entfernungen andere Methoden
entwickelt werden, die teilweise den zuletzt genannten ähneln.
0.4. Messunsicherheit
Jede Messung einer physikalischen Größe ist mit einem mehr oder weniger großen Messfehler behaftet, selbst wenn es sich nur um eine „Banalität“ wie die Messung des Abstandes
12
Vgl. WEBB, Stephen: Measuring the Universe – The Cosmological Distance Ladder. Springer, 1999, S. 15f.
7
0.4. MESSUNSICHERHEIT
Einführung
h
2m
115m
105m
3m
Abb. 0.6.: Berechnung der Pyramidenhöhe: (115 + 105) : 3 = h : 2
zwischen zwei Punkten handelt. Misst man eine Größe mehrmals, so weichen die Ergebnisse im Allgemeinen sowohl voneinander als auch vom zu bestimmenden „wahren“ Wert ab.
Ziel einer jeden Messung ist es nicht nur, den wahren Wert möglichst exakt zu ermitteln,
sondern auch die Messunsicherheit angeben zu können und zu minimieren.
Man unterscheidet zwischen systematischen und statistischen Messfehlern.
• Systematische Messfehler sind einseitig gerichtet und werden etwa durch unberücksichtigte Umwelteinflüsse (z. B. der Auftrieb der Luft bei sehr präzisen Gewichtsbestimmungen), unvollkommene Messinstrumente (z. B. Eichfehler oder nichtlineare
Kennlinien) oder deren Rückwirkung auf das gemessene System (z. B. entzieht ein
Thermometer der Probe Wärme) verursacht. Sie können in vielen Fällen durch ergänzende Messungen oder durch eine eingehende Analyse der verwendeten Messgeräte
und der Messverfahren erkannt und korrigiert werden.
• Statistische Messabweichungen sind zufällig, nicht einseitig gerichtet und führen zu
einer Streuung der Messergebnisse. Sie haben eine Summe von vielen variierenden
und kleinen Störungen wie etwa äußere Einflüsse (z. B. kurzzeitige Temperatur- oder
Luftdruckschwankungen), die Unzulänglichkeit des Experimentators (z. B. Schätzungen oder Betrachtung der Messskala unter einem anderen Winkel) oder den
statistischen Charakter der Messgröße selbst (z. B. der radioaktive Zerfall von Atomkernen) als Ursache. Statistische Fehler können durch Wiederholung der Messung
minimiert werden.
8
0.4. MESSUNSICHERHEIT
Einführung
In der Praxis werden meist mehrere Messungen durchgeführt und von den erhaltenen
Messwerten angenommen, dass sie „normalverteilt“ sind (d. h. die gaußsche Glockenkurve
als Wahrscheinlichkeitsdichte haben). Anschließend werden der arithmetische Mittelwert
(X) und die Standardabweichung (S) der Messwerte berechnet. Innerhalb des Bereiches
X ± S liegt dann mit 68 % Sicherheit der nächste Messwert der gesuchten Größe. Als
Messergebnis wird der Mittelwert ± seinem mittleren Fehler als Messunsicherheit angegeben. Dieser ist um den Faktor
1
p
n
(mit n für die Anzahl der Messungen) kleiner als
die Standardabweichung. Um ein Resultat also doppelt so genau zu erhalten, muss man
viermal so viele Messungen durchführen. Der „wahre“ Wert der Messung liegt mit 68 %
Wahrscheinlichkeit in dem durch Mittelwert und Messabweichung definierten Bereich.
Wenn man eine Aussage mit größerer statistischer Sicherheit machen will, muss man die
doppelte oder gar dreifache Standardabweichung als Messunsicherheit verwenden. Dann
beträgt statistische Sicherheit 95,5 % bzw. 99,7 %.
Da astronomische Entfernungsbestimmungen meist aufeinander aufbauen, bringt eine
Messabweichung auf den unteren Sprossen der Entfernungsleiter die Fehlerfortpflanzung
als großes Problem mit sich. Diese bewirkt einen Messfehler von bis zu 50 % bei der
Bestimmung großer Distanzen.
9
1. Erste Sprosse: Die Erde
1.1. Antike
Bis in die griechische Antike war die Astronomie untrennbar mit Mythologie und Religion verbunden. Neben der astrologischen Deutung dienten Himmelsbeobachtungen aber
auch zur Bestimmung der Tageszeit und für den Kalender. In Ägypten etwa wurde mit
dem Aufgang des Sirius, des hellsten Sterns am Nachthimmel, das jährlich bevorstehende Nilhochwasser in Zusammenhang gebracht. Babylonische Priester konnten mit Hilfe
unzähliger aufgezeichneter Beobachtungsdaten schon mögliche Termine für Mond- und
Sonnenfinsternisse vorhersagen, die sie als Omen deuteten.
Ein weitergehendes Naturverständnis entwickelten die Griechen. Sie hatten sich nicht nur
fundierte geometrische Kenntnisse angeeignet, sondern besaßen auch eine grundlegend
neue Einstellung zu den Wissenschaften: Das Streben nach Erkenntnis wurde als ein
Selbstzweck betrachtet, losgelöst von praktischer Nutzanwendung.
Während laut Thales von Milet (um 600 v. Chr.) die Erde noch flach war und auf dem
Wasser schwamm, behauptete sein Schüler Anaximander, sie sei ein Zylinder, um welchen
sich auf konzentrischen Kreisen Sonne, Mond und Sterne bewegen. Pythagoras von Samos
(um 550 v. Chr.) war der erste, der insbesondere aus ästhetischen Gründen die Erde für
eine Kugel hielt. Aristoteles (4. Jh. v. Chr.), der Lehrer Alexanders des Großen, begründete
die Kugelgestalt in seinem Buch Über das Himmelsgewölbe1 u. a. folgendermaßen:
„Ihre Form aber muß nothwendig die einer Kugel sein. [...]; bei den monatlichen Formveränderungen nimmt der Mond alle möglichen Arten der Abtheilung
an (er wird nämlich sowohl geradlinig, als auch rings gewölbt, als auch hohl),
hingegen bei den Finsternissen hat er die abgrenzende Linie immer gewölbt, so
daß, wofern er sich wegen des Vorliegens der Erde verfinstert, wohl der Umfang
der Erde, welcher ein kugelförmiger ist, die Ursache dieser Form sein dürfte; –
als auch ferner durch die Erscheinung der Sterne ist nicht bloß augenfällig, daß
1
gr. ΠERI OΥRANOΥ (peri uranu)/lat. DE CAELO
10
1.1. ANTIKE
Erste Sprosse: Die Erde
die Erde rund ist, sondern auch daß sie, was die Größe betrifft, nicht eben groß
ist; nämlich wenn wir mit uns nur eine geringe Ortsveränderung gegen Süden
oder Norden vornehmen, so wird in merklicher Weise der Horizont schon
ein anderer, so daß die Sterne über unserem Haupte eine große Veränderung
zeigen [...]; denn einige Sterne werden wohl in Aegypten und in der Nähe von
Cypern gesehen, hingegen in den nördlichen Gegenden nicht, und auch diejenigen unter den Sternen, welche in nördlichen Gegenden immerwährend am
Himmel stehen, haben in jenen Orten gleichfalls einen Untergang. Folglich ist
aus diesem nicht blos klar, daß die Form der Erde rund ist, sondern auch daß sie
die einer nicht großen Kugel ist; denn außerdem würde es nicht so schnell bei
einer nur so kurzen Ortsveränderung es bemerklich machen. Daher diejenigen,
welche annehmen, es hänge die Gegend um die Säulen des Herakles [Anm.:
Gibraltar] mit jener um Indien zusammen, und es sei auf diese Weise das Meer
Eines, hiermit nicht allzu Unglaubliches anzunehmen scheinen; sie behaupten
dies aber, indem sie als Beweismittel auch die Elephanten anführen, nämlich
daß an jenen beiden äußersten Gegenden sich diese Thiergattung finde, eben
als trete dies bei den beiden äußersten Punkten wegen ihres gegenseitigen
Zusammenhanges ein.“2
Auch die Beobachtung von auslaufenden Schiffen, bei denen zuerst der Rumpf und danach
erst der Mast verschwinden, oder die unterschiedlichen Tageszeiten, zu denen dieselbe
Mondfinsternis etwa in Spanien und in Persien beobachtet wurde, ließen diesen Schluss zu.
Entgegen der heute weit verbreiteten Ansicht, dass im mittelalterlichen Abendland die Vorstellung der
Erde als Kugel in Vergessenheit geraten war und man zu Zeiten von Kolumbus von einer flachen Erdscheibe
ausging, weil dies die Lehre der Kirche gewesen sei, wurde die Kugelgestalt in Europa seit der Antike
weitgehend nicht mehr in Frage gestellt. Nicht zuletzt, weil Aristoteles im Hoch- und Spätmittelalter als
größte Autorität in Fragen der Naturwissenschaft galt. Lediglich einzelne Autoren wie z. B. die Kirchenväter
Laktanius und Severianus von Gabala vertraten die Meinung, die Erde sei eine Scheibe. Diese fanden jedoch
bis in die Neuzeit wenig Beachtung. Erst im 19. Jahrhundert wurden diese Schriften wiederentdeckt und der
Mythos der „flachen Erde“ im Mittelalter mit der Absicht populär gemacht, diese kirchlich geprägte Epoche
als „primitiv“ und die Kirche als wissenschaftsfeindlich darzustellen. Über diesen Sachverhalt wurden in den
letzten Jahrzehnten zahlreiche Werke verfasst.3 4 5
2
ARISTOTELES; PRANTL, Karl (Hrsg.): Opera „Werke“, Band 2, gr. ΠERI OΥRANOΥ (peri uranu)/lat. DE
CAELO „Über das Himmelsgewölbe“. Neudr. d. Ausgabe Leipzig 1857, Scientia Verlag Wien, 1978, 2. Buch,
Kapitel 14, S. 177ff.
3
PRAUSE, Wolfgang: Niemand hat Kolumbus ausgelacht – Fälschungen und Legenden der Geschichte
richtiggestellt. Econ, 1966.
4
SIMEK, Rudolf: Erde und Kosmos im Mittelalter – Das Weltbild vor Kolumbus. C. H. Beck, 1992.
5
KRÜGER, Reinhard: Eine Welt ohne Amerika. Weidler, 2000.
11
1.1. ANTIKE
Erste Sprosse: Die Erde
Abb. 1.1.: Hauptmeridian der hellenistischen Geographie
Es lag daher also nahe, sich über die Ausmaße der Erdkugel Gedanken zu machen. Aristoteles schrieb darüber gleich im Anschluss an obiges Zitat: „Auch behaupten diejenigen unter
den Mathematikern, welche die Größe des Umfangs zu berechnen versuchten, derselbe sei
ungefähr vierhunderttausend Stadien.“6 „Das entspricht etwa 63 000 Kilometern[7 ] und ist
über die Hälfte mehr als nach modernen Messungen. Über das Verfahren, mit dem sie zu
dieser Zahl gelangten, sind keine Aufzeichnungen erhalten.“8
Die erste in ihrer Methode überlieferte Messung des Erdradius führte wahrscheinlich
Dikaiarchos9 , ein Schüler von Aristoteles, im Zuge der Schaffung einer Landkarte durch.
Er beobachtete in den Städten Syene und Lysimachia am Hellespont10 , von denen er annahm, dass sie am selben Meridian, dem Hauptmeridian der hellenistischen Geographie (s.
Abb. 1.1), lagen, die unterschiedliche Höhe von Sternbildern. Der Astronom und Geograph
Kleomedes (um 370 n. Chr.) beschreibt diese Methode folgendermaßen:
6
ARISTOTELES: De Caelo, 2. Buch, Kapitel 14, S. 183.
Da in der Antike je nach Ort und Zeit viele verschiedene Stadienmaße definiert waren, ist heute neben der
genauen Länge des gewählten Stadions oft auch schwer rekonstruierbar, auf welchen Standard sich die
Überlieferung einer Entfernung bezieht.
8
FERGUSON, Kitty: Das Maß der Unendlichkeit – Auf der Suche nach den Grenzen des Universums. Aus dem
Englischen von Friedrich Griese. Econ, 2000, S. 17.
9
Vgl. BIALAS, Volker: Erdgestalt, Kosmologie und Weltanschauung – Die Geschichte der Geodäsie als Teil der
Kulturgeschichte der Menschheit. Konrad Wittwer, 1982, S. 28.
10
antiker Name für die Dardanellen
7
12
1.1. ANTIKE
Erste Sprosse: Die Erde
„Denn die Bewohner von Lysimachia sehen den Kopf des Drachen über ihrem
Scheitel, die Bewohner von Syene aber den Krebs. Von dem durch Lysimachia
und Syene gehenden Meridian aber ist der zwischen dem Drachen und dem
Krebs befindliche Bogen der 15. Teil, wie durch die ‚Schattenjäger‘11 dargetan
wird.“12
Die Entfernung zwischen den Städten wurde mit 20 000 Stadien angenommen, so dass sich
ein Erdumfang von 300 000 Stadien (= 29 700 km bei Verwendung des Herodoteischen
Stadions von 99 m) ergab, was wiederum nur drei Viertel von heutigen Messergebnissen
ist.13
Zu einem besseren Wert kam der 100 Jahre nach Aristoteles geborene Eratosthenes.
1.1.1. Eratosthenes
Nach dem Tod Alexanders des Großen 323 v. Chr. in Babylon zerfiel sein sich bis zum Indus
erstreckendes Großreich in mehrere so genannte Diadochenreiche, also Reiche unter der
Herrschaft seiner ehemaligen Feldherrn. Dieses Staatensystem hatte bis zum Auftreten
des römischen Reichs im östlichen Mittelmeerraum Bestand und bot den Rahmen für die
kulturelle Entfaltung des Hellenismus.
Eratosthenes wurde 284 v. Chr. in Kyrene, einer Stadt im heutigen Libyen, das wie
Ägypten und Palästina zum Reich des Diadochen Ptolemaios gehörte, geboren. In Alexandria, einer Hafenstadt am Nildelta und Hauptstadt des Ptolemäerreichs, wurde zu jener
Zeit die berühmte Bibliothek gegründet, die bald Athen als Zentrum der geistigen Welt
ablöste und bis zu ihrem verheerenden Brand 47 v. Chr. das gesammelte damalige Wissen
enthielt. Dennoch genoss Eratosthenes seine Ausbildung in Griechenland in der von Platon
gegründeten Akademie und im Lyzeum von Aristoteles. Bis zur Jahrhundertmitte hatte
er einige philosophische und literarische Werke verfasst, aufgrund derer er zur Erziehung
des Thronfolgers an den Königshof nach Alexandria berufen wurde. Dort etablierte er sich
245 v. Chr. zum Direktor der Bibliothek, die bis dahin schon hunderttausende Schriftrollen
angehäuft hatte. Von seinen Kollegen bekam er die Spitznamen „Beta“ und „Pentathlos“,
was soviel wie „Nummer Zwei“ und „Fünfkämpfer“ bedeutet, weil er ein Universalgelehrter,
aber in keiner Disziplin der Wissenschaft ein Spezialist war. Er sammelte das gesamte
11
ein antikes astronomisches Messinstrument bestehend aus zwei Stiften, von denen einer seinen Schatten
auf den anderen wirft
12
KLEOMEDES; CZWALINA, Arthur (Hrsg.): Die Kreisbewegung der Gestirne. Akademische Verlagsgesellschaft
Leipzig, 1927, 1. Buch, 8. Kapitel: Die Erde eine Kugel, S. 28.
13
Vgl. BIALAS: Erdgestalt, Kosmologie und Weltanschauung, S. 29.
13
1.1. ANTIKE
Erste Sprosse: Die Erde
geographische Wissen seiner Zeit und verbesserte die damalige Weltkarte mit einer Art
Längen- und Breitengradnetz. Weiters war Eratosthenes dank der profunden Grundlagen,
die Euklid rund 25 Jahre vor seiner Geburt in seinem berühmten, aus 13 Büchern bestehenden Werk Elemente14 zusammengefasst hatte, und seiner Bekanntschaft zu Archimedes,
dessen Werke auch im 16. und 17. Jahrhundert noch bei der Entwicklung der höheren
Analysis von Bedeutung waren, auf dem neuesten Stand der Geometrie.
Von seinen eigenen Werken Über die Vermessung der Erde15 oder über ein Verfahren
zur Bestimmung von Primzahlen – heute noch „Sieb des Eratosthenes“ genannt – sind
nur mehr Fragmente erhalten. Die wichtigsten Belege über sein Schaffen, vor allem die
über die Bestimmung des Erdradius, sind wiederum bei Kleomedes, aber auch bei dem
Geschichtsschreiber und Geographen Strabon (um Christi Geburt) in seinem historisch
bedeutsamen Werk Geographie16 zu finden.
Neben seinem für wissenschaftliche Entdeckungen fruchtbaren Umfeld und seinem weit
gefächerten Wissen ermöglichte ihm erst die Information, dass in Syene (in der Nähe des
heutigen Assuan) am Tag der Sommersonnwende zur Mittagszeit die Sonnenstrahlen bis
auf den Grund eines Brunnens drangen bzw. ein Obelisk oder eine Mauer keinen Schatten
warfen, seine erfolgreiche Messung des Erdumfangs. Eratosthenes schloss daraus richtig,
dass Syene in der Nähe des nördlichen Wendekreises liegt und die Sonne deshalb an diesem
Mittag genau im Zenit stand, während sie in Alexandria leicht südlich davon zu sehen war,
was der Schattenwurf eines senkrecht aufgestellten Stabes bewies. Eratosthenes schätzte
den Winkel, um den die Sonne vom Zenit abwich, mit Hilfe einer Art Sonnenuhr, bei der der
Gnomon17 in der Mitte einer Skaphe18 (halbkugelförmige Schale mit einer Winkeleinteilung
auf der Innenseite, s. Abb. 1.2), platziert war, auf ein Fünfzigstel eines vollen Kreises, was
7, 2◦ entspricht. Unter der damals schon weit verbreiteten Annahme der Kugelgestalt der
Erde, der Parallelität von einfallenden Sonnenstrahlen aufgrund der großen Entfernung
der Sonne (ohne diese Hypothese ließe sich der unterschiedlich lange Schatten auch wie
beim Durchschreiten des Lichtkegels einer Straßenlaterne erklären: nur direkt unter der
Lampe wirft man keinen Schatten) und der Tatsache, dass Syene am selben Längengrad
wie Alexandria liegt (s. Abb. 1.1), berechnete Eratosthenes den Erdumfang, wie Abbildung
1.3 veranschaulicht. Er wusste, was Euklid im ersten Buch seiner Elemente in Satz 29 „die
Winkel an geschnittenen Parallelen“ nannte, nämlich dass der von ihm gemessene Winkel
14
gr. ΣTOIXEIA (stoicheia)
gr. ΠERI THΣ ANAMETRHΣEOΣ THΣ Γ EΣ (peri tes anametreseos tes ges)
16
gr. Γ EΩΓ PAΦIKA (geographika)
17
gr. γνώµων (gnómon) „Schattenzeiger“
18
gr. σκαϕoς (skaphos) „Wanne, Schale“
15
14
1.1. ANTIKE
Erste Sprosse: Die Erde
Abb. 1.2.: Skaphe
Sonnenlicht
a
Gnomon in Alexandria
a
Brunnen in Syene
Äqu
ato
r
Abb. 1.3.: Erdumfang nach Eratosthenes
15
1.1. ANTIKE
Erste Sprosse: Die Erde
zugleich der dem Kreisbogen Syene – Assuan gegenüberliegende Winkel im Erdmittelpunkt
ist. Außerdem war ihm klar, dass bei einem Kreis gleich großen Zentriwinkeln gleich lange
Kreisbögen gegenüberliegen. Kleomedes beschreibt Eratosthenes’ Vorgehensweise weiter:
„Der innerhalb der Höhlung der Sonnenuhr liegende Kreisbogen hat also zum
Umfang des zu ihm gehörigen ganzen Kreises dasselbe Verhältnis wie der
Meridianbogen von Alexandria bis Syene zum Umfang der Erde. [...] Es muß
also auch die Entfernung zwischen Alexandria und Syene der 50ste Teil des
Erdumfangs sein. Diese Entfernung beträgt aber 5 000 Stadien. Der Erdumfang
beträgt also 250 000 Stadien. [...] Es wird also der Erddurchmesser über 80 000
Stadien groß sein, da er der dritte Teil des Erdumfangs ist. Dies ist die Methode
des Eratosthenes.“19
Es ist umstritten, wie lang das Stadion ist, das Eratosthenes verwendete, weil es zu
seiner Zeit etwa sieben gebräuchliche Stadionmaße gab. Das Ergebnis kann deshalb
zwischen 37 125 Kilometer für das später sogar nach ihm benannten Eratosthenische
Stadion (= 148,5 m), das babylonischen Ursprungs ist, und 46 250 Kilometer für das
Römische (= 185 m) liegen20 . Falls er das Ägyptische Stadion (= 157,5 m) gebrauchte, kam
Eratosthenes auf 39 375 Kilometer, was mit heutigen Messungen recht gut übereinstimmt:
40 009 Kilometer über die Pole und 40 079 Kilometer um den Äquator.21 Donald Engels
rechtfertigt in einem Artikel22 anschaulich das ca. 185 Meter messende Stadion, er nennt
es das Attische, und argumentiert gegen die heute noch oft zitierten oberen Angaben.
Es stellt sich natürlich auch die Frage, wie Eratosthenes auf die Entfernung zwischen
Alexandria und Syene kam. Man vermutet, dass er mehrere Quellen wie die ägyptische
Landmessung, Schrittzähler und Erzählungen von Nilfahrten und Kamelkarawanen miteinander verglich und so die 5 000 Stadien abschätzte. Dass Eratosthenes sich seiner bedingten
Genauigkeit bewusst war, sieht man an der Tatsache, dass er seinen errechneten Wert von
250 000 auf 252 000 Stadien aufrundete, wie bei Strabon nachzulesen ist. Dieser Wert
eignet sich nämlich besser für die Berechnung der damals in Hexekosta (ein Hexekoston
entspricht einem Sechzigstel des gesamten Kreisumfangs, also 6◦ ) ausgedrückten Breite
der Erdzonen und war durch π = 3 teilbar, obwohl Archimedes in seinem Werk über die
Kreismessung π schon zwischen 3 10
(≈ 3,141) und 3 17 (≈ 3,143) bestimmt hatte23 . Diese
71
19
KLEOMEDES: Die Kreisbewegung der Gestirne, 1. Buch, Kapitel 10: Die Größe der Erde, S. 36.
Vgl. BACHMANN, Emil: Wer hat Himmel und Erde gemessen? Ott, 1965, S. 34.
21
Vgl. FERGUSON: Das Maß der Unendlichkeit, S. 30.
22
ENGELS, Donald: The Length of Eratosthenes’ Stade. The American Journal of Philology, 106 1985, Nr. 3.
23
Vgl. BIALAS: Erdgestalt, Kosmologie und Weltanschauung, S. 34.
20
16
1.1. ANTIKE
Erste Sprosse: Die Erde
Unsicherheiten lassen auch über die Tatsachen hinwegblicken, dass Syene weder genau
am selben Längengrad wie Alexandria noch exakt am nördlichen Wendekreis liegt.
Konrad Miller24 beharrt auf der Exaktheit des Ergebnisses des Eratosthenes. Er schreibt,
dass es sich bei den 252 000 Stadien nicht um eine Aufrundung handle, sondern dass
◦
Eratosthenes statt der 7 15 (=
360◦
)
50
◦
eher 7 17 gemessen habe und der Wert 250 000 Stadien
nur falsch überliefert sei. Dieses Ergebnis wäre aufgrund der Einteilung der Skaphe in
Hexekosta keineswegs schwieriger abzulesen. Weiters behauptet er, dass die Entfernung von
Alexandria bis zum Wendekreis zu 5000 Stadien von Schrittzählern und mit Messschnüren
ziemlich genau gemessen wurde. Zuletzt hält auch er an dem 157,5 Meter messenden
Stadion fest, das zu dem sehr genauen Wert von 39 690 Kilometer für den Erdumfang
führt.
1.1.2. Poseidonios
Eine weitere Messung des Erdradius wird dem griechischen Philosoph Poseidonios (ca. 135 –
51 v. Chr.) aus Apameia im heutigen Syrien zugeschrieben (u. a. wieder bei Kleomedes).
Nach dem Studium in Athen ließ er sich auf der Insel Rhodos nieder, wo er sich ausgiebig
mit Philosophie, Geschichte und Geographie auseinander setzte. Zu den Hörern seiner
Vorlesungen zählten u. a. wichtige Persönlichkeiten wie Cicero und Pompeius.
Wie schon Dikaiarchos und Eratosthenes benutzte er bei seiner Methode einen Teil
des damaligen Hauptmeridians, nämlich die Strecke zwischen Rhodos und Alexandria (s.
Abb. 1.1), die er mit 5 000 Stadien annahm (die Entfernung ist in Wirklichkeit kürzer).
Auf den zugehörigen Zentriwinkel kam er durch Abschätzung der Kulminationshöhe des
Sterns Canopus, dem zweithellsten Stern des Nachthimmels, der auf Rhodos kurzzeitig
gerade noch am Horizont zu sehen ist, in Alexandria hingegen „hat der Stern zur Zeit
seiner Kulmination eine Höhe gleich dem vierten Teile eines Zwölftels des Tierkreises,
also gleich dessen 48sten Teile [Anm.: entspricht 7, 5◦ ; der Winkel ist in Wirklichkeit aber
kleiner; d. h. die Messfehler kompensieren sich beinahe]. Es folgt also, dass das Stück
des Meridians, das über der Strecke zwischen Rhodos und Alexandria gelegen ist, der
48ste Teil des ganzen Meridians ist, weil der Horizont der Rhodier und der Horizont der
Bewohner von Alexandria um den 48sten Teil des Bogens der Kreisperipherie voneinander
abweichen.“25 Daher kam er zum Ergebnis, dass der Erdumfang etwa 240 000 Stadien
beträgt, was unter Verwendung des Eratosthenischen Stadions 35 640 Kilometern entspricht
(s. Abb. 1.4). In der Überlieferung Strabons beträgt die Strecke von Rhodos nach Alexandria
24
25
Vgl. MILLER, Konrad: Die Erdmessung im Altertum und ihr Schicksal. Strecker und Schröder, 1919, S. 5ff.
KLEOMEDES: Die Kreisbewegung der Gestirne, 1. Buch, Kapitel 10: Die Größe der Erde, S. 34.
17
1.1. ANTIKE
Erste Sprosse: Die Erde
Horizont
in Alexandria
Horizont
auf Rhodos
Rhodos
Alexandria
a
Äqu
ato
a
r
Licht vom
Stern Canopus
Abb. 1.4.: Erdumfang nach Poseidonios
aufgrund der Verwendung des Babylonisch-Persischen Stadions (= 198 m) nur 3 750
Stadien, der Erdumfang also nur 180 000 Stadien, was jedoch derselben Länge entspricht.
Diese Tatsache ist historisch besonders erwähnenswert, weil von Claudius Ptolemäus
in seinem Werk Einführung in die Geographie26 der kleinere Wert von 180 000 Stadien
überliefert wurde, die dann als römische Stadien interpretiert wurden. Dies hat einen
Erdumfang von umgerechnet nur 33 408 Kilometern zur Folge. Insbesondere Kolumbus
stützte sich bei seinen Überlegungen über den schnellsten Seeweg nach Indien neben der
Annahme eines viel zu breiten Anteils der Ökumene27 (die bekannte Landmasse Europa,
Afrika und Asien) an der gesamten Erde auf den zu kleinen Wert, was bekanntlich zur
Wiederentdeckung Amerikas führte.
26
27
gr. ΓEΩΓPAΦIKE ΥΦEΓEΣIΣ (geographike hyphegesis)
gr. oικoυµένη (oikouméne) „bebautes od. bewohntes Land, Erdkreis“
18
1.2. MITTELALTER
Erste Sprosse: Die Erde
1.2. Mittelalter
Die nächste dokumentierte Messung des Erdradius führten im Jahre 725 n. Chr. die Astronomen Nankung Yueh und I-Hsing in China durch, die wie Eratosthenes die Schattenlängen
von Gnomonen an verschiedenen Orten verglichen.
Rund 100 Jahre später beauftragte der Kalif Al Ma’mūn u. a. den Astronomen Al Farghānı̄
mit der Messung des Erdradius. Dieser bestimmte in der Wüste Singar in Arabien einen
Meridianbogen von 2◦28 , indem zwei Vermessungsteams von einem festgelegten Punkt
solange nach Norden bzw. Süden gingen, bis sich der Höhenwinkel, unter dem sie den
Polarstern sahen, um einen Grad veränderte (s. Abb. 1.5).
Abb. 1.5.: Arabische Meridiangradmessung im 9. Jh.
Das Ergebnis dieser ersten so genannten „Meridiangradmessung“, der Mittelwert der
beiden mittels Messstangen gemessenen Strecken, betrug 56 23 arabische Meilen. Bei Verwendung der „gewöhnlichen“ arabischen Meile (= 1920 m) ergibt das umgerechnet 108,8
Kilometer, der ganze Erdumfang also 39168 Kilometer29 . Aber auch über die benutzte arabische Meile herrscht Uneinigkeit. „Dieses Resultat ist nicht mehr – wie in der Antike – auf
die Ungenauigkeit der Streckenmessung, sondern auf die Unsicherheit in der Bestimmung
der Polhöhendifferenz zurückzuführen“30 .
Der arabische Geometer Al Bı̄rūnı̄ (973 – 1048) beschrieb in seinem Buch Al-Qânûn
al-Mas’ûdî (ein Sultan Mas’ūd gewidmetes Handbuch der Astronomie) um 1000 n. Chr.
noch einen anderen Weg, um den Radius der Erde zu erfassen. Er berichtete, dass er
von einen 652 Ellen hohen Berg an der indischen Küste einen Tiefenwinkel von 330 zum
Meereshorizont bestimmt habe. Daraus errechnete er über ein rechtwinkeliges Dreieck
den Erdradius zu 3 333 arabischen Meilen und den Meridiangrad zu 58,2 arabischen
Die Winkeleinteilung des Kreises in 360◦ hatte sich seit dem 2. Jh. v. Chr. immer mehr etabliert.
Vgl. MILLER: Die Erdmessung im Altertum und ihr Schicksal, S.34f.
30
BIALAS: Erdgestalt, Kosmologie und Weltanschauung, S. 62.
28
29
19
1.3. NEUZEIT
Erste Sprosse: Die Erde
a
h
r
r
a
Abb. 1.6.: Berechnung des Erdradius nach Al Bı̄rūnı̄: Aus cos α =
r
r+h
ergibt sich r =
cos α
h.
1−cos α
Meilen (s. Abb. 1.6). Es ist zweifelhaft, ob Al Bı̄rūnı̄ diese Messung in Anbetracht der guten
Übereinstimmung mit der früheren arabischen Gradmessung wirklich durchführte, weil das
Messverfahren letztlich wohl an der Messgenauigkeit des Tiefenwinkels scheitern würde.
1.3. Neuzeit
Es sollte bis 1525 dauern, also 3 Jahre nachdem die Kugelgestalt der Erde durch die Weltumsegelung Magellans bewiesen war, bis eine bessere Messung des Erdradius vollbracht
wurde. Der französische Arzt Jean Fernel (1497 – 1558) fuhr mit einem Wagen solange
von Paris aus nach Norden, bis der Höhenwinkel der Mittagssonne um einen Grad kleiner
war. Dabei zählte er die Umdrehungen des Rades, dessen Umfang ihm bekannt war, und
berechnete daraus nach Abzug eines nicht näher genannten Betrages wegen Neigungen
und Biegungen des Weges eine Gradbogenlänge von 111,23 Kilometer, woraus sich der
Erdumfang zu 40 034 Kilometer ableiten ließ. Die hohe Genauigkeit lässt aufgrund der
primitiven Mittel wohl eher auf einen glücklichen Zufall schließen.
1615 führte der Niederländer Snellius (eigentlich Willebrord van Roijen Snell; 1580 –
1626), auch bekannt für die Entwicklung des optischen Brechungsgesetzes, die erste
20
1.3. NEUZEIT
Erste Sprosse: Die Erde
moderne, wenn auch noch etwas ungenaue, Triangulation durch. Die geographischen
Breiten seiner beiden Ausgangspunkte Bergen op Zoom im Süden und Alkmaar im Norden
Hollands leitete er aus Polarsternbeobachtungen ab. Mit Hilfe eines Netzes von 33 Dreiecken, wobei als Eckpunkte weit sichtbare Erhöhungen oder Türme gewählt wurden, und
der Messung mit Holzlatten einer kurzen Basis in der Mitte des Meridianbogens kam er
auf eine Länge von 107,33 Kilometer für den Meridiangrad, was zu einem Erdumfang von
38 638,8 Kilometer führen würde. Zwar lagen vor ihm schon bessere Angaben vor, aber
die Art der Streckenmessung war doch revolutionär und stellt noch heute die Basis für die
Landvermessung dar.
1669 beauftragte Ludwig XIV. die französische Akademie der Wissenschaften mit der
Messung eines Meridianbogens und der Schaffung eines neuen Maß- und Gewichtsystems,
das als Grundlage die Länge des Sekundenpendels in Paris habe (vgl. Abschn. 0.2). Der
Geometer Jean Picard (1620 – 1682) wurde mit der Aufgabe betraut und veröffentlichte
1682 seine Ergebnisse: Der gefundene Meridiangrad war 111,211 Kilometer, der Erdumfang
daher 40 035,96 Kilometer lang. Picard bewegte sich wie schon Fernel auf dem Längengrad
zwischen Paris und Amiens und benützte hierfür die von Snellius entwickelte Triangulation
erstmals in Verbindung mit einem Fernrohr mit Fadenkreuz und Schraubenmikrometer.
„Mit den Messungen von Picard sind, historisch gesehen, die geodätischen Unternehmungen, die für die Figur der Erde eine wohlgeformte Kugel zugrunde gelegt haben,
abgeschlossen.“31 Einen Überblick über die einzelnen Ergebnisse bietet Tabelle 1.1.
Tab. 1.1.: Historische Entwicklung der Einschätzung des Erdumfangs bis Picard
Zeit
um 350
um 300
um 225
um 100
um 820
1525
1615
um 1670
v. Chr.
v. Chr.
v. Chr.
v. Chr.
Person
Methode
Aristoteles
Dikaiarchos
Eratosthenes
Poseidonios
Al Mamūn
Fernel
Snellius
Picard
unbekannt
Zenitschätzung von Sternbildern
Messung der Sonnenhöhe
Schätzung von Fixsternhöhen
erste Meridiangradmessung
Radumdrehungen
Triangulation
Triangulation mit Fadenkreuz
Erdumfang
[Stadien32 ]
[km]
400 000
63 000
300 000
29 700
250 000
46 250
240 000
35 640
39 168
40 034
38 639
40 036
(?)
(?)
(?)
Einige Jahre vor Picards Messungen stellte Isaac Newton (1642jul. /1643greg. – 1727) sein
Gravitationsgesetz auf. Er wollte es rechnerisch überprüfen, indem er die den Mond auf
seiner Kreisbahn um die Erde haltende Zentripetalkraft (FZ ) mit der Gravitationskraft (FG )
auf der Erde verglich. Unter der Annahme, dass die mittlere Distanz des Mondes von der
31
32
BIALAS: Erdgestalt, Kosmologie und Weltanschauung, S. 103.
Für die Umrechnung der Stadien wurden die jeweils wahrscheinlichsten Maße verwendet.
21
1.3. NEUZEIT
Erste Sprosse: Die Erde
Erde (d) dem 60-fachen Erdradius (r) entspreche (s. Abschn. 2.1), versuchte er sinngemäß
folgendes zu zeigen:
FZ = mω2 d
mit m für die Mondmasse und ω für die Winkelgeschwindigkeit des Mondes, also ω =
2π
T
mit T für die siderische Umlaufzeit des Mondes (27d 7h 43min ), also
FZ = m(
2π
T
)2 d,
wird gleichgesetzt mit Newtons Gravitationskraft
FG = γ
Mm
d2
wobei γ für die Gravitationskonstante und M für die Erdmasse steht.
Nach Ersetzen von d durch 60r und Kürzen von m bleibt:
(
2π
T
)2 60r = γ
M
(60r)2
Die rechte Seite kann nun umgeschrieben werden in:
.
g
602
mit g =
γM
r2
für die Erdbeschleuni-
gung. Daraus kann nun der Wert von g berechnet werden:
g = 60
3
4 π2
T2
r
Dieser Wert soll nun gleich dem mit Hilfe des Sekundenpendels erlangten Wert für g sein:
g = π2 l
(leicht auszurechnen
q aus der Formel für die Schwingungsdauer eines mathematischen
Pendels: T = 2π gl ) mit l für die Länge des Sekundenpendels, die Christiaan Huygens,
mehr für seine Werke über Wellenoptik bekannt, für Paris zu 0,994 Meter ermittelt hatte.
Für den Erdradius nahm Newton anfangs noch den von Galilei überlieferten Wert des
Ptolemäus an und kam deshalb auf ein falsches Ergebnis. Erst die Erdmessung von Picard
bestätigte neben anderen Anhaltspunkten die Richtigkeit von Newtons Theorie, die er in
seinem Hauptwerk Mathematische Grundlagen der Naturphilosophie33 1686 veröffentlichte.
33
lat. PHLOSOPHIAE NATURLALIS PRINCIPIA MATHEMATICA
22
1.4. HEUTE
Erste Sprosse: Die Erde
Ebenfalls in diesem Werk erklärte Newton die Beobachtung des französischen Astronomen Jean Richer (1630 – 1696) bezüglich der längeren Schwingungsdauer von Pendeluhren
in der Nähe des Äquators. Dieser bemerkte bei 1672 in Cayenne (Französisch-Guyana)
durchgeführten Messungen, die eigentlich der Bestimmung der Marsparallaxe galten (s.
Abschn. 2.3.3), dass ein aus Paris mitgebrachtes Sekundenpendel täglich um mehr als zwei
Minuten gegen die mittlere Sonne zurückblieb. Um die richtige Zeit zu erhalten, musste
das Pendel um 3,9 mm gekürzt werden. Da Giovanni Domenico Cassini (1625 – 1712), der
die Marsobservationen in Paris leitete, schon 1666 beobachtet hatte, dass der Planet Jupiter
an den Polen abgeflacht ist, vermutete Richer eine ähnliche Abplattung der Erde. Newton
untermauerte die Vermutung, indem er rechnerisch nachwies, dass andere Einflüsse wie
die Entfernung und Lage zur Drehachse und die daraus resultierenden Kräfte oder die
Längenausdehnung des Pendelstabes aufgrund der tropischen Temperaturen nicht für
die Unstimmigkeiten ausreichen. „Daher verhält sich der Durchmesser der Erde auf der
Äquatorebene zu ihrem Durchmesser durch die Pole wie 230 zu 229.“34 Dieses Verhältnis
stellt einen oberen Grenzwert dar, da Newton eine homogene Massenzusammensetzung
der Erde voraussetzte, während – wie wir heute wissen – die Dichte zum Erdzentrum
zunimmt. Huygens berechnete unter der Annahme, dass die Dichte zum Erdmittelpunkt
so groß wird, dass die weiter außen liegende Masse vernachlässigbar wäre, den unteren
Grenzwert des Verhältnisses der Durchmesser zu 578 zu 577.
Es folgten mehrere Gradmessungen an Orten möglichst unterschiedlicher Breite wie
Lappland und Peru, aus deren Ergebnisse sich ein Unterschied von etwa 43 Kilometern
zwischen den Durchmessern am Äquator und durch die Pole berechnen ließ, was einem
Verhältnis von 298 zu 297 entspricht.
1.4. Heute
Heutzutage lassen sich die Erdmaße mit Hilfe der Satellitenvermessung (Satellite Laser
Ranging, kurz SLR) auf den Millimeter genau bestimmen. Dabei werden Laser-Impulse mit
Teleskopen auf so genannte Retroreflektoren35 , die auf Satelliten angebracht sind, „geschossen“. Mit Atomuhren wird dann die Laufzeit bis zur Rückkehr der Impulse gemessen. Aus
dieser Laufzeit lässt sich dann die Entfernung zwischen Teleskop und Satellit berechnen.
Durch die Vernetzung solcher Messungen an mehreren Orten der Erde kann man nicht
34
NEWTON, Isaac; DELLIAN, Ed (Hrsg.): Philosophiae Naturalis Principia Mathematica „Mathematische
Grundlagen der Naturphilosophie“. Meiner, 1988, S. 206.
35
Spiegel, die einfallendes Licht wieder Richtung Lichtquelle reflektieren.
23
1.4. HEUTE
Erste Sprosse: Die Erde
nur auf den genauen Erdradius schließen, sondern auch auf seismische Aktivitäten und
Veränderungen der Erdrotation. Laut dieser Messungen beträgt der mittlere Erdradius,
also der Radius einer volumengleichen Kugel, 6 371 000,785 Meter, der Äquatorradius des
mittleren Erdellipsoids nach dem World Geodetic System von 1984 (WGS84), mit dem
z. B. das Global Positioning System (GPS) arbeitet, 6 378 137,000 Meter, der Polradius
6 356 752,314 Meter. Der Äquatorumfang dieses Ellipsoids misst demnach 40 075 017
Meter, der Polumfang 40 007 862 Meter.
24
2. Zweite Sprosse: Das Sonnensystem
Wenn wir mit freiem Auge den Nachthimmel beobachten, könnten wir die Vorstellung
einer sich um eine starre Achse nach Westen drehenden Himmelskugel erlangen, an der
unterschiedlich helle Lichtpunkte fixiert sind. Jede andere Konfiguration würde nämlich
den scheinbaren Abstand zwischen diesen so genannten Fixsternen im Laufe der Nacht
verändern, es sei denn, sie wären unvorstellbar weit entfernt. Doch dann müssten sie sich
mit unvorstellbarer Geschwindigkeit um die Erde drehen. Oder dreht sich doch die Erde
um ihre Achse? Aber dann würden wir diese Rotation wohl spüren, die Wolken blieben
am Himmel zurück und ein kerzengerade hochgeschossener Pfeil fiele weit hinter dem
Schützen herab. Weniger absurd erscheint doch das Modell der Fixsternsphäre.
Wenn wir eine Uhr zu Hilfe nehmen und beispielsweise genau zu Mitternacht einen
gewissen Stern aufgehen sehen, dann können wir in der darauf folgenden Nacht denselben
Stern schon knapp 4 Minuten vor Mitternacht am Horizont entdecken. Das Firmament1
scheint sich also ungefähr alle 23 Stunden und 56 Minuten um unsere Erde zu drehen,
also etwas schneller als sich die Sonne durchschnittlich von einem Höchststand zum
nächsten bewegt2 . Mit anderen Worten bedeutet das, dass sich die Sonne relativ zu den
Sternen Richtung Osten bewegt. Diese Bewegung fällt uns normalerweise nicht auf, weil
sie mit weniger als einem Grad pro Tag erfolgt und wir bestenfalls bei Sonnenaufgang oder
-untergang die Sonne und andere Sterne gleichzeitig sehen. In einem Jahr durchläuft sie
so die komplette Himmelssphäre auf einer scheinbaren Bahn, die Ekliptik oder Tierkreis
genannt und in 12 gleich große Abschnitte zu 30◦ unterteilt wird, die Tierkreiszeichen3 .
Dieser hat eine Neigung von 23,5◦ gegenüber dem Äquator der Sternsphäre.
Auch der Mond scheint nicht an dieser Kugel befestigt zu sein. Er durchläuft sie in etwas
mehr als 27 Tagen, 7 Stunden und 43 Minuten, also mit einer Winkelgeschwindigkeit von
mehr als 13◦ pro Tag.
1
lat. firmamentum „Befestigungsmittel, Stütze“
Definition eines mittleren Sonnentages, von dem die Dauer einer Sekunde ursprünglich abgeleitet wurde.
3
Vor etwa 2 000 Jahren stimmte der Zeitraum der astrologischen Sternzeichen noch mit der Stellung der
Sonne im Bereich des jeweiligen Sternbildes überein. Heute hat er sich aufgrund der Präzession der
Erdachse um ungefähr einen Monat verschoben.
2
25
Zweite Sprosse: Das Sonnensystem
Bei genauerem Hinsehen über einen längeren Zeitraum fallen neben diesen zwei Gestirnen noch andere Lichtpunkte auf, die sich immer in einem gürtelförmigen Bereich
des Himmels, der sich beiderseits etwa 8◦ weit von der Ekliptik erstreckt, befinden und
ihre Lage relativ zu den Fixsternen unterschiedlich schnell verändern. Ihre scheinbaren
Bewegungen, genauer gesagt die Projektionen der Bahnen auf das Firmament, sind sehr
kompliziert: Während sich die Sonne fast gleichförmig auf der Ekliptik bewegt, wird der
fortschreitende Lauf dieser „Wandergestirne“ nach Osten durch Intervalle rückläufiger
Bewegung nach Westen hin unterbrochen. Deshalb wurden sie Planeten4 genannt. Sie
lassen sich nach ihren Umlaufzeiten durch den Tierkreis folgendermaßen anordnen: Der
langsamste, Saturn genannt5 , benötigt etwa 29,5 Jahre, bis er wieder im selben Sternbild
zu sehen ist, d. h. er bewegt sich durchschnittlich um ca. 20 innerhalb von 24 Stunden
relativ zu den Fixsternen; Jupiter braucht fast 12 Jahre für einen Umlauf (entspricht etwa 50
pro Tag), und Mars beinahe 2 Jahre (entspricht mehr als 0,5◦ pro Tag). Venus und Merkur
durchlaufen die Himmelssphäre gleich schnell wie die Sonne, um die sie in unregelmäßigen Zeitabständen mit einer Elongation von 45◦ bzw. 28◦ zu pendeln scheinen, weshalb
insbesondere Venus im Volksmund je nach dem, ob sie westlich oder östlich der Sonne
zu sehen ist, Morgen- oder Abendstern genannt wird. Ihre Namen sind die lateinischen
Übersetzungen der jeweiligen griechischen Gottheiten Kronos (Saturn), Zeus (Jupiter),
Ares (Mars), Aphrodite (Venus) und Hermes (Merkur)6 .
Da der Mond Sterne und manchmal auch Planeten oder sogar die Sonne verdeckt, ist die
Überlegung nachvollziehbar, dass dieser der Erde am nächsten ist (vgl. Abschn. 0.1). Schon
im antiken Griechenland hatte man diesen Gedankengang und schloss weiters darauf,
dass „langsamere Gestirne“ weiter entfernt sind als „schnellere“. So kommt man zu der
Reihung Mond, dann Merkur, Venus und Sonne, gefolgt von Mars, Jupiter und Saturn für
die beobachtbaren Wandergestirne.
Diese Reihenfolge verbunden mit der Meinung, dass sich Merkur und Venus zwischen Mond und Sonne
bewegen (diese Ansicht war spätestens nach Ptolemäus verbreitet), erklärt die Ordnung unserer Wochentage,
die in romanischen Sprachen und teils auch noch im Deutschen und Englischen nach diesen Gestirnen
benannt sind. Antike Astrologen teilten jeder Stunde des Tages eine dieser Gottheiten zu. Ein Tag wurde
nach dem Gott der ersten Stunde benannt. Der Mond, das erdnäheste Gestirn, war der ersten Stunde
des ersten Tages zugeordnet, deshalb der Name „Mond-Tag“ (franz. lundi/span. lunes/ital. lunedì von lat.
luna „Mond“; engl. monday). Die zweite Stunde war die des Merkurs, die dritte die der Venus usw., bis
in der 25. Stunde, also der ersten Stunde des zweiten Tages, zum wiederholten Mal Mars an der Reihe
war (franz. mardi/span. martes/ital. martedì). Analog gelangt man für Mittwoch zum Tag des Merkurs
gr. πλανήτης (planétes) „umherirrend“
Uranus und Neptun sind mit freiem Auge nicht sichtbar.
6
Vgl. WEBB: Measuring The Universe, S. 26.
4
5
26
Zweite Sprosse: Das Sonnensystem
(franz. mercredi/span. miércoles/ital. mercoledì), für Donnerstag zum Tag des Jupiters (franz. jeudi/span.
jueves/ital. giovedì), für Freitag zum Tag der Venus (franz. vendredi/span. viernes/ital. venerdì), für Samstag
zum Tag des Saturns (engl. saturday) und für Sonntag zum Tag der Sonne (engl. sunday)7 8 .
Auch um die Größenordnung der Distanz zum Mond und der Sonne abzuschätzen, kann
uns ein Blick zum Himmel behilflich sein.
Dass die zwei Gestirne nicht nur einige dutzend Kilometer von uns entfernt sind, beweist
eine fehlende Größenveränderung, wenn wir uns beispielsweise zu oder von einem tief
stehenden Mond hin- bzw. wegbewegen. Außerdem gibt es keine merkliche Bewegungsparallaxe, etwa bei einer Fahrt mit dem Zug oder Auto: Mond und Sonne „gehen immer hinter
den Bergen mit“.
Als nächstes müssen wir die Einsicht erlangen, dass es sich beim Mond wie bei der Erde
um eine von der Sonne beleuchtete Kugel handelt. Neben der oben erwähnten Tatsache,
dass sich der Mond schneller übers Firmament bewegt als die anderen Wandergestirne, was
uns nahe legt, ihn als eigenständigen sich um die Erde drehenden Körper zu betrachten,
weisen noch seine Phasen und die Orientierung der Sichelform darauf hin. Genauer gesagt
zeigt die Streckensymmetrale der beiden Spitzen der Mondsichel immer Richtung Sonne9 .
Auch lässt sich die Krümmung des Terminators (= Schattenlinie auf dem Mond) nur
durch eine gewölbte Oberfläche und die Beleuchtung durch die Sonne schlüssig erklären.
Und welche geometrische Figur läge in Anbetracht der Kugelgestalt der Erde, die wir ja
spätestens seit Aristoteles’ Argumentation akzeptieren, näher als wiederum eine Kugel?
Mit dieser Erkenntnis bekommt das Himmelsgewölbe jedoch plötzlich eine neue Dimensionierung. Besonders bei einer schmalen Mondsichel, also wenige Tage vor und nach
Neumond, wenn der Mond und die Sonne nicht weit voneinander am Himmel zu sehen
sind, begreift man, dass die zwei Gestirne nicht mehr in nahe zueinander liegenden Sphären um die Erde kreisen können. „Der Mond schwebt ‚vorn‘ und die Sonne sinkt in einen
tiefen Abgrund in den Raum zurück, wobei sie sich zu furchtbarer Größe aufbläht“10 , weil
sie uns ja etwa gleich groß erscheint wie der Mond.
Wenn wir nun den Winkel zwischen Sonne und Mond und die Breite der Mondsichel genau mäßen, dann könnten wir mit etwas Mathematik über das Dreieck Sonne – Mond – Erde
herausfinden, wie viel mal weiter weg die Sonne als der Mond entfernt ist; offensichtlich
um ein Vielfaches.
7
Die Bezeichnungen für Samstag und Sonntag in romanischen Sprachen gehen auf jüdische (Sabbat) bzw.
christliche Einflüsse (Tag des Herrn) zurück.
8
Vgl. STUMPFF, Karl: Die Erde als Planet. Springer, 1939, S. 78.
9
Dass uns das nicht immer so erscheint, hängt mit einer optischen Täuschung zusammen. Mehr dazu
beispielsweise unter www.karlheinzschott.de.
10
WAGENSCHEIN, Martin: Natur physikalisch gesehen. Diesterweg, 1960, S. 45.
27
2.1. ANTIKE
Zweite Sprosse: Das Sonnensystem
Mond
90°
Sonne
b
Mond
Sonne
90°
b
Erde
Abb. 2.1.: Winkel zwischen Sonne und Halbmond
Bei Halbmond fällt uns diese Rechnung besonders leicht, weil wir dann wissen, dass der
Winkel Sonne – Mond – Erde ein rechter ist, wie Abbildung 2.1 zeigt.
2.1. Antike
2.1.1. Aristarch
Diese Idee hatte auch Aristarch von Samos (ca. 310 – 230 v. Chr.), ein älterer Zeitgenosse des
Eratosthenes. Sein einziges schriftlich erhaltenes Werk Über die Größen und Entfernungen
[der Sonne und des Mondes] 11 beginnt mit folgenden Hypothesen und daraus abgeleiteten
Behauptungen:12
1. „Dass der Mond sein Licht von der Sonne erhält.“
2. „Dass die Erde im Verhältnis eines Mittelpunktes zu der Sphäre ist, in der
sich der Mond bewegt13 .“
ΠERI MEΓ EΘΩN KAI AΠOΣTHMATΩN [HΛIOΥ KAI ΣEΛHNHΣ] (peri megethon kai apostematon [heliu
kai selenes])
12
Folgende zwei Aufzählungen frei übersetzt nach HEATH, Thomas: Aristarchus of Samos – The ancient
Copernicus. Sandpiper Books, 1997, S. 353 (Originaltext im Anhang).
13
Wörtlich ‚Sphäre des Mondes‘
11
28
2.1. ANTIKE
Zweite Sprosse: Das Sonnensystem
3. „Dass, wenn der Mond uns halbiert erscheint, der Großkreis, der den
dunklen und hellen Anteil des Mondes trennt, in Richtung unseres Auges
liegt14 .“
4. „Dass, wenn der Mond uns halbiert erscheint, sein Abstand zur Sonne
dann um ein Dreißigstel eines Quadranten kleiner ist als ein Quadrant15 .“
5. „Dass die Breite des Schattens (der Erde) (die) von zwei Monden ist.“
6. „Dass der Mond den fünfzehnten Teil eines Tierkreiszeichens verdeckt16 .“
„Wir sind nun in der Lage, folgende Behauptungen zu beweisen:“
1. „Die Entfernung der Sonne von der Erde ist größer als 18-mal, aber kleiner
als 20-mal, die Entfernung des Mondes (von der Erde); dies folgt aus der
Hypothese über den halbierten Mond.“
2. „Der Durchmesser der Sonne hat dasselbe Verhältnis (wie oben genannt)
zum Durchmesser des Mondes17 .“
3. „Der Durchmesser der Sonne hat zum Durchmesser der Erde ein größeres
Verhältnis als 19 zu 3, aber ein kleineres als 43 zu 6[18 ]; dies folgt aus
dem entdeckten Verhältnis zwischen den Entfernungen, der Hypothese
über den Schatten und der Hypothese, dass der Mond den fünfzehnten
Teil eines Tierkreiszeichens verdeckt.“
Aristarch rechnete wie alle Mathematiker zu jener Zeit mit Verhältnissen von ganzen
Zahlen und kam durch rein geometrische Beweise zu den genannten Grenzverhältnissen.
Wir werden jedoch die Trigonometrie zu Hilfe nehmen:
Wörtlich ‚sich zu unserem Auge neigt‘ [...].
◦
I. e. 90◦ − 90
= 87◦ .
30
◦
30
16
◦
I. e. 15 = 2 ; Archimedes schreibt in seinem Werk Über schwimmende Körper und die Sandzahl (Archimedes,
ed. Heiberg, ii, S. 248, 19 [Vgl. Übersetzung von Arthur Czwalina, Akademische Verlagsgesellschaft Leipzig,
1925, Die Sandzahl, 1. Kapitel, S. 69]), Aristarch ‚entdeckte, dass die Sonne der 720ste Teil des Tierkreises
zu sein scheint‘; Aristarch ermittelte diesen viel korrekteren Wert von 12 ◦ für den Winkeldurchmesser der
Sonne oder des Mondes (denn er nahm für beide denselben an: siehe Satz 8 [Heath: Aristarchus of Samos,
S. 383]) offensichtlich nach Erscheinen der uns überlieferten Abhandlung. Archimedes seinerseits
beschreibt an der gleichen Stelle eine ungefähre Methode der Beobachtung, mit der er herausfand, dass
der Durchmesser der Sonne weniger als der 164ste Teil und mehr als der 200ste Teil des rechten Winkels
ist [Anm.: D. h. zwischen 33 und 27 Bogenminuten]. Siehe [Heath: Aristarchus of Samos] S. 311
17
Pappus gibt dieses zweite Ergebnis gleich nach dem ersten an, nämlich vor der Bemerkung ‚dies folgt aus
der Hypothese... ‘. [Anm.: Pappus von Alexandria (um 300 n. Chr.) kommentierte im sechsten Buch seiner
Mathematischen Sammlungen u. a. die Arbeiten von Aristarch] [...] das zweite Ergebnis folgt [jedoch] nicht
aus der Hypothese über den halbierten Mond alleine; es beruht auch auf einer anderen Annahme, und
zwar, dass die Sonne und der Mond offenbar denselben Winkeldurchmesser haben [...].
r
18
d. h. 6, 3̇ < rS < 7, 16̇
14
15
E
29
2.1. ANTIKE
Zweite Sprosse: Das Sonnensystem
ad 1.:
Den Winkel β in Abbildung 2.1 schätzte er laut vierter Hypothese mit 87◦ ab. Weil im
rechtwinkeligen Dreieck cos β =
Ankathete
Hypotenuse
=
dM
dS
(d steht von jetzt an immer für die Distanz
des im Index abgekürzten Himmelskörper zur Erde, r für dessen Radius) gilt, erhält man
für die Relation zwischen dem Abstand Erde – Sonne und dem Abstand Erde – Mond
dS : dM =
1
cos 87◦
≈ 19,1.
ad 2.:
Siehe Abbildung 2.2.
Sonne
19
Mond
1
Abb. 2.2.: Weil Sonne und Mond ungefähr unter demselben Winkel erscheinen, wie man am besten
während einer Sonnenfinsternis beobachten kann, folgt aus dem Strahlensatz und dem
Ergebnis der ersten Behauptung: rS : rM = dS : dM ≈ 19,1
ad 3.: Für die Aussage über den Durchmesser der Sonne ist die fünfte Hypothese
über die Breite des Erdschattens an der Stelle, an der ihn der Mond während einer
Mondfinsternis durchläuft, ausschlaggebend. Diese Hypothese stellte Aristarch auf, als er
eine Mondfinsternis maximaler Dauer beobachtete, also eine, bei der der Mond genau den
Mittelpunkt des Erdschattens durchquert. Er maß die Zeit vom Eintreten des Mondes in den
Erdschatten bis zu seiner vollständigen Verdeckung. Diese Zeitspanne war, wie er feststellte,
ebenso lang wie die, in der der Mond völlig verdeckt war. Daraus folgerte Aristarch, dass
die Breite des Erdschattens dort ungefähr das Zweifache des Monddurchmessers beträgt (s.
Abb. 2.3).
30
2.1. ANTIKE
Zweite Sprosse: Das Sonnensystem
Mond
1
2
3
Sonne
Erde
4
Abb. 2.3.: Aristarchs Abschätzung des Durchmessers des konischen Erdschattens relativ zum Monddurchmesser durch Messung der Zeitabstände zwischen folgenden Ereignissen während
einer Mondfinsternis: Eintritt in den Erdschatten (1), Beginn der vollständigen Verdeckung (2), Ende der vollständigen Überdeckung (3), Austritt aus dem Erdschatten (4)
Mond
Erde
Sonne
Abb. 2.4.: Mit Hilfe des Strahlensatzes und des Verhältnisses dS : dM = 19 : 1 wird rM und rS mit rE
in Verbindung gebracht: (rE − 2rM ) : 1 = (rS − 2rM ) : 20
Zusammen mit dem Ergebnis der ersten Behauptung führt der Strahlensatz, wie in
Abbildung 2.4 ersichtlich ist, zur Relation
(rE − 2rM ) : 1 = (rS − 2rM ) : 20.
Durch Einsetzen des Ergebnisses der zweiten Behauptung rS = 19rM ergibt sich
rM ≈ 0,35rE
bzw.
rS ≈ 6,7rE .
In Worten heißt das, dass der Radius des Mondes rund 35 % des Erdradius beträgt und
der Radius der Sonne ca. 6,7-mal so groß wie der der Erde ist (dieselben Werte gelten
natürlich auch für die Durchmesser).
Die Entfernungen von Sonne und Mond zur Erde erlangt man mit den in der sechsten
Hypothese abgeschätzten 2◦ Winkeldurchmesser von Sonne und Mond. Denn mit einer
einfachen trigonometrischen Rechnung ergibt sich, dass die Radien von Sonne und Mond
jeweils rund 1,75 % ihrer Entfernung von der Erde betragen (weil tan 1◦ ≈
31
2π
360◦
≈ 0,0175).
2.1. ANTIKE
Zweite Sprosse: Das Sonnensystem
Erdradius
Mondradius
Sonnenradius
Winkeldurchmesser Mond/Sonne
Abstand Erde – Mond
Abstand Erde – Sonne
Aristarch
1
0,35
6,70
2◦
300
20
80
384 1 537
heute19
1
0,27
110
310 /320
60
23 455
Tab. 2.1.: Aristarchs Ergebnisse in Erdradien im Vergleich zu heutigen Messungen
Mit den vorigen Ergebnissen für die Durchmesser der Gestirne erhält man so für den
Abstand Erde – Sonne etwa den 384-fachen Erdradius und für den Abstand Erde – Mond
den 20-fachen Erdradius. Mit dem besseren Wert von
1◦
2
für die Winkeldurchmesser kommt
man ungefähr auf den 1537-fachen bzw. 80-fachen Erdradius.
Aristarch gab erstaunlicherweise keine Werte für diese Entfernungen an, obwohl er
alle dafür nötigen Informationen zur Verfügung hatte. Anscheinend war er mehr an der
Geometrie seiner Argumente interessiert als an den resultierenden Zahlenwerten.
Die Messungen Aristarchs waren nicht sehr genau, wie Tabelle 2.1 aufzeigt. Insbesondere
der in der vierten Hypothese mit 87◦ angegebene Winkel zwischen Sonne und Halbmond,
der die Grundlage für alle Ergebnisse darstellt, beträgt in Wirklichkeit etwa 89◦ 510 , also
fast 90◦ , sodass die Sonne in Wahrheit fast 400-mal so weit von der Erde entfernt ist
wie der Mond und deswegen auch fast 400-mal so groß ist. Die exakte Messung des
Winkels zwischen Sonne und Halbmond würde sich auch heute noch als problematisch
erweisen, weil es kein leichtes Unterfangen ist, den Mittelpunkt der Sonne und des Mondes
anzuvisieren. Auch der Zeitpunkt des Halbmondes muss auf die Minute genau bestimmt
werden, weil der Mond wegen der Bewegung um die Erde in 27 Tagen 7 Stunden und 43
◦
Minuten seine Position um mehr als eine halbe Bogenminute pro Minute ändert ( 27d360
≈
7h 43min
3300 /min ). Und schon eine kleine Änderung des Winkels verändert das Ergebnis maßgeblich
– schließlich unterscheidet sich der wirkliche Winkel nur um 9 Bogenminuten vom rechten
Winkel, was für die Sonne eine unendliche Entfernung bedeuten würde. Wie in den
folgenden Kapiteln ersichtlich wird, entwickelte sich der Abstand zwischen Erde und Sonne
zu so einer wichtigen Längeneinheit, dass sie der Name „Astronomische Einheit“ (AE)
schmückt – die Bestimmung ihres tatsächlichen Wertes sollte jedoch erst mehr als 2 000
Jahre nach Aristarch gelingen.
Besser bekannt ist Aristarch heute dafür, dass er einer der ersten Vertreter des heliozentrischen Weltbildes war. Dazu ermutigt wurde er wohl von dem Ergebnis seiner Messungen,
19
Mittlere Radien/Winkeldurchmesser/Abstände
32
2.1. ANTIKE
Zweite Sprosse: Das Sonnensystem
weil es ihm vernünftiger erschien, dass sich der kleinere Körper (die Erde) um den größeren
(die Sonne) bewegt. Zu Lebzeiten stieß er mit seinen Theorien jedoch kaum auf Anerkennung, erst Kopernikus wurde fast 2 000 Jahre später durch seine Schriften inspiriert.
Erwähnt wurde seine Hypothese u. a. von Archimedes:
„Aristarch von Samos gab die Erörterungen gewisser Hypothesen heraus, in
welchen aus den gemachten Voraussetzungen erschlossen wird, daß der Kosmos
ein Vielfaches der von mir angegebenen Größe sei. Es wird nämlich angenommen, daß die Fixsterne und die Sonne unbeweglich seien, die Erde sich um die
Sonne, die in der Mitte der Erdbahn liege, in einem Kreis bewege, [...]“20
In diesem Werk findet man nicht nur einen Wert für den Durchmesser des Kosmos, sondern
auch eine abgeschätzte obere Grenze für die Entfernung der Sonne, nämlich 10 000
Erdradien. Jedoch dienten diese Angaben Archimedes nur seinen Rechnungen mit großen
Zahlen und beruhten kaum auf astronomischen Messungen.
2.1.2. Hipparch
Der nächste nennenswerte Erfolg zur Bestimmung der Mond- und Sonnenentfernung
gelang Hipparch von Nicäa (ca. 190 – 120 v. Chr.), einem der bedeutendsten Astronomen
der Antike.
Zu seinen großen Errungenschaften zählen die Fertigung eines umfassenden und präzisen Sternenkatalogs, die Entdeckung der Präzession der Erdachse21 durch Vergleich von
aktuellen Sternpositionen mit überlieferten Daten und die Zusammenstellung einer Tabelle
von Kreissehnenlängen zum zugehörigen Zentriwinkel (Chordentafel22 ), die die Grundlage
für die moderne Trigonometrie bildeten.
Während seine Vorgänger sich mit geometrischen Theorien zufrieden gaben, die Bewegungen der Himmelskörper prinzipiell erklären zu können, schuf Hipparch mit Hilfe
der Epizykeltheorie Modelle zur Vorhersage der Bahnen von Sonne und Mond. Diese
bis Kopernikus verwendete Theorie zur Erklärung der rückläufigen Planetenbewegung
wurde wahrscheinlich schon von Apollonius von Perge im 3. Jh. v. Chr. aufgestellt und von
Ptolemäus im 2. Jh. n. Chr. perfektioniert, mehr dazu in nächsten Abschnitt.
20
ARCHIMEDES; CZWALINA, Arthur (Hrsg.): Über schwimmende Körper und die Sandzahl. Akademische
Verlagsgesellschaft Leipzig, 1925, Die Sandzahl, 1. Kapitel, S. 67.
21
Neueren Untersuchungen zufolge war die Präzession auch schon Aristarch bekannt (s. Rawlins, Dennis:
Aristarchos’ pre-Hipparchan Precession. DIO (The International Journal of Scientific History) 9.1, 1999,
S. 30ff).
22
lat. chorda „Sehne“
33
2.1. ANTIKE
Zweite Sprosse: Das Sonnensystem
Von Hipparchs Werken ist nur ein kurzer Kommentar aus seiner Jugend erhalten geblieben. Die Hauptquellen für seine Leistungen bilden der berühmte Almagest von Ptolemäus
und ein Kommentar zu selbigem Werk von Pappus von Alexandria aus dem 4. Jahrhundert,
in dem auch seine Ergebnisse für die Entfernungen von Sonne und Mond erwähnt und
seine Vorgehensweise dafür angedeutet werden:
„Hipparch, der nicht nur unsicher war, wie groß die Parallaxe[23 s. Abb. 2.5] der
Sonne ist, sondern auch, ob sie überhaupt eine Parallaxe hat, nahm im ersten
Buch von ‚Über Größen und Entfernungen‘ an, dass die Erde das Verhältnis eines
Punktes und Zentrums zur Sonne [wörtlich: zur Sphäre der Sonne] hat. Zu
einer Zeit, bei der Verwendung der von ihm angeführten Eklipse[24 ], nahm er
an, dass sie die kleinste Parallaxe hat, zu einer anderen Zeit jedoch nahm er eine
größere Parallaxe an. Folglich kamen die Verhältnisse der Mondentfernungen
verschieden heraus. In Buch 1 von ‚Über Größen und Entfernungen‘ nutzt er
die folgende Beobachtung: Eine Sonnenfinsternis, die im Gebiet des Hellespont
eine exakte Eklipse der ganzen Sonne war, sodass kein Teil von ihr sichtbar
war, während in Alexandria in Ägypten ungefähr vier Fünftel des Durchmessers
verdeckt waren. Mittels des oben genannten zeigt er im Buch 1, dass, in
Einheiten des Erdradius, die kleinste Entfernung des Monds 71, und die größte
83 ist. Folglich ist die mittlere 77. Das Vorhergehende gezeigt, sagt er am
Ende des Buches: ‚In dieser Arbeit haben wir unsere Demonstrationen bis zu
diesem Punkt ausgeführt. Aber nehmen Sie nicht an, dass die Frage nach der
Mondentfernung schon gründlich untersucht worden ist. Denn es bleibt auch
einiges zu diesem Thema zu untersuchen, mittels dessen, wie gezeigt wird, die
Mondentfernung weniger sein wird als das, was wir gerade ausrechneten.‘ Also
gibt Hipparchus auch selbst zu, dass er alles in allem bezüglich der Parallaxen
nicht sicher sein kann. Denn er selbst zeigt im Buch 2 von ‚Über Größen und
Entfernungen‘ nach vielen Überlegungen, dass, in Einheiten des Erdradius, die
23
In der Astronomie versteht man unter der Parallaxe den Winkel zwischen zwei Geraden, die von
verschiedenen Standorten („Basislinie“) auf einen Punkt (ein Himmelsobjekt) gerichtet sind. Dies ist auch
der Winkel, unter dem diese Basislinie vom beobachteten Punkt aus erscheint. Man unterscheidet je nach
Basislinie zwischen geozentrischer bzw. täglicher (also durch unterschiedliche Position auf der Erde oder
durch die Erddrehung verursacht), horizontaler (spezielle geozentrische Parallaxe mit dem Erdradius,
genauer gesagt, dem Halbmesser des Äquators, als Basislinie) und jährlicher Parallaxe (also mit zwei
Astronomischen Einheiten als Basislinie, z. B. Sternparallaxe). Einfacher als eine direkte Messung ist meist
der Vergleich mit einem weit entfernten Objekt im Hintergrund, dessen Parallaxe nicht messbar ist. Vgl.
Abschn. 0.1: Bewegungsparallaxe, Querdisparität.
24
gr. κλιψις (ekleipsis) „Finsternis“
34
2.1. ANTIKE
Erde
Zweite Sprosse: Das Sonnensystem
a
Sonne
a
Abb. 2.5.: Die so genannte horizontale Parallaxe der Sonne (α) entspricht dem Winkel, unter dem
man den Erdradius (genauer: Radius des Äquators) von der Sonne (genauer: Sonnenmittelpunkt) aus sehen würde bzw. dem maximalen Winkel, um den die Sonne einem
Beobachter auf der Erdoberfläche im Vergleich zu einem theoretischen Beobachter im Erdmittelpunkt (oder auf dessen der Verbindungslinie zur Sonne) verschoben erscheint. Weiß
r
man diesen Winkel, so weiß man wegen der trigonometrischen Beziehung sin α = dE auch
S
den Sonnenabstand. Für kleine Winkel gilt in guter Näherung: sin α ≈ tan α ≈ α [rad],
was gleichbedeutend damit ist, dass der Distanzunterschied von weit entfernten Objekten
zum Beobachter auf der Erdoberfläche und zum Erdmittelpunkt vernachlässigbar ist.
Mindestentfernung des Monds 62, die mittlere 67 13 , und die Sonnenentfernung
490 ist. Es ist klar, dass die größte Entfernung des Monds 72 23 sein wird.“25
Erst im vergangenen Jahrhundert ist es den Historikern Swerdlow und Toomer gelungen,
Hipparchs Methoden zu rekonstruieren.
Bei dem ersten Verfahren verwendete Hipparch die ihm überlieferte Information, dass bei
der Sonnenfinsternis am 14. März 189 v. Chr. die Sonne am Hellespont völlig verdunkelt
war, während in Alexandria nur vier Fünftel verdeckt waren. Mit den ihm bekannten
Breiten vom Hellespont und Alexandria und der Annahme, dass die beiden Orte am selben
Meridian liegen, sowie der Deklination26 des Mondes zur Zeit der Finsternis, die er mit
den ihm zur Verfügung stehenden Mitteln schon auszurechnen vermochte, konnte er
folgendermaßen die gesuchten Entfernungen bestimmen: Er ging davon aus, dass die
Entfernung zur Sonne so groß sei, dass ihre (geozentrische) Parallaxe nicht messbar bzw.
vernachlässigbar klein wäre. Demzufolge wäre die tägliche Parallaxe des Mondes alleine
dafür verantwortlich, ob es sich um eine totale oder eine teilweise Sonnenfinsternis handelt.
Das hieße, dass ein Fünftel des Winkeldurchmessers der Sonne gerade den Parallaxenwinkel
des Mondes beschreibt, wie Abbildung 2.6 zeigt. Unter der Annahme, dass die Eklipse am
Himmelsmeridian über dem Hellespont bzw. Alexandria, also um die Mittagszeit stattfand,
liegen alle wichtigen Punkte in einer Ebene. Abbildung 2.7 veranschaulicht die Situation.
M steht für den Mond-, E für den Erdmittelpunkt, H für Hellespont, A für Alexandria, Z für
die Zenitrichtung am Hellespont, ϕ für die jeweilige geographische Breite. Statt Hipparchs
25
Frei übersetzt nach TOOMER, G. J.: Hipparchus on the distances of the sun and moon. Archive for History of
Exact Sciences, 14 1974, Nr. 2, S. 126f (Originaltext im Anhang).
26
Winkelabstand vom Himmelsäquator
35
2.1. ANTIKE
Zweite Sprosse: Das Sonnensystem
Mond
m
Hellespont
m
Alexandria
Sonnenlicht
Abb. 2.6.: Bestimmung der geozentrischen Mondparallaxe bei einer teilweisen Sonnenfinsternis:
Vom Hellespont aus sieht man den Mond und die Sonne (genauer gesagt einen Punkt des
Mond- bzw. Sonnenumrisses) in derselben Richtung, während in Alexandria der Mond
im Vergleich zur Sonne um den Parallaxenwinkel µ verschoben erscheint.
Z
z’
H
q
A
z
E
d
d’
m
d
Abb. 2.7.: Hipparchs erste Methode zur Bestimmung der Mondentfernung
36
M
2.1. ANTIKE
Zweite Sprosse: Das Sonnensystem
Chordfunktion verwenden wir den uns bekannten Sinus27 . Das Dreieck AH M ist bestimmt
durch die Seite
ϕ − ϕA
AEH
= 2rE sin( H
),
2
2
den Parallaxenwinkel µ und durch den Winkel θ . Letzterer lässt sich wie folgt berechnen:
AH = 2rE sin
θ = Z HA − ζ0
EHA =
Z HA = 180◦ − EHA
180◦ − AEH
2
=
180◦ − (ϕH − ϕA )
2
1
⇒ Z HA = 90◦ + (ϕH − ϕA )
2
Da der Mond sicher einige Erdradien entfernt ist, ist ζ0 näherungsweise ζ und deshalb mit
ζ = ϕH − δ:
1
θ ≈ Z HA − ζ = 90◦ − (ϕH + ϕA ) + δ
2
Mit Hilfe des Sinussatzes kann man nun d 0 berechnen:
Aus
d0
=
sin θ
AH
sin µ
folgt
d0 =
AH sin θ
sin µ
=
2 sin(
ϕH −ϕA
2
) sin θ
sin µ
rE .
Die Entfernung des Mondes beträgt dann ungefähr
d ≈ d + rE = (1 +
0
2 sin(
ϕH −ϕA
2
) sin(90◦ − 12 (ϕH + ϕA ) + δ)
sin µ
)rE .
Hipparch verwendete wahrscheinlich folgende Zahlenwerte28 : Für die Breitengrade ϕH ≈
41◦ und ϕA ≈ 31◦ , für die Deklination des Mondes δ ≈ −3◦ und für die Mondparallaxe
zwischen dem Hellespont und Alexandria µ =
360◦
,
650·5
da er für die Winkeldurchmesser der
Sonne den 650sten Teil des Kreises verwendete. Damit kam er für d auf ca. 71 Erdradien.
27
28
chord(α) = 2 sin( α2 )
Vgl. TOOMER: Archive for History of Exact Sciences 14 [1974], S. 132f.
37
2.1. ANTIKE
Zweite Sprosse: Das Sonnensystem
Hipparch wusste schon, dass der Abstand des Mondes im Laufe eines Monats variiert29
und erklärte dies mit Hilfe der Epizykeltheorie. Die 71 Erdradien interpretierte er als
Minimalabstand und berechnete zu diesem Wert mit dem von ihm verwendeten Verhältnis
des Deferentenradius des Mondes zu seinem Epizykelradius (3 122 12 : 247 12 )30 die oben
genannte mittlere und maximale Entfernung des Mondes.
Hipparch war sich der Ungenauigkeit seiner Parallaxenmethode bewusst. Schon eine
kleine Änderung für das Verhältnis der teilweisen Sonnenfinsternis in Alexandria auf
3
4
5
6
oder
verursacht eine Vergrößerung bzw. Verkleinerung aller Distanzen um ca. 20 %. Außerdem
dürfte ihm bekannt gewesen sein, dass die besagte Eklipse eben nicht um die Mittagszeit
in Alexandria und am Hellespont stattfand, was zu einem noch größeren d 0 führen würde.
Dass es sich mit gegebenem µ bei d 0 nämlich um ein Minimum handelt, wird dadurch
ersichtlich, dass auch θ im Meridian minimal ist. Verständlich wird dies, wenn man sich
die Finsternis z. B. kurz vor Sonnenuntergang, M also weit entfernt von der verwendeten
Ebene AEH vorstellt. Dann ist θ = M HA ≈ M AH (also 4M HA gleichschenklig) und
deshalb θ ≈ 90◦ − 12 µ, also fast 90◦ .
Deshalb entwickelte er ein zweites Verfahren, das eine Verbesserung von Aristarchs
Mondfinsternis-Methode darstellt. Er verwendete nicht die Dichotomie (= Phase, bei der ein
nicht selbst leuchtendes Gestirn zur Hälfte beleuchtet wird) des Mondes für die Bestimmung
des Entfernungsverhältnisses, sondern wie bei der Sonnenfinsternis-Methode die Annahme,
dass die geozentrische Sonnenparallaxe zu klein wäre, um messbar zu sein. Diesmal nahm
er sie jedoch nicht als vernachlässigbar klein an, sondern ordnete ihr den Wert 70 zu,
der gleichbedeutend mit einer Sonnenentfernung von etwa 490 Erdradien ist (tan 70 ≈
1
).
490
Die 7 Bogenminuten begründete er damit, dass dies ein vernünftiger Wert für eine
gerade noch messbare tägliche Parallaxe sei. Weiters maß Hipparch für die Breite des
Erdschattens in mittlerer Mondentfernung 2,5 Monddurchmesser (nicht wie Aristarch nur
2 Monddurchmesser).
Abbildung 2.8 zeigt Hipparchs Modell für den Querschnitt einer Sonnen- und Mondfinsternis in einer Zeichnung („Eklipsendiagramm“). M und E stellen wieder die Mittelpunkte
des Mondes bzw. der Erde dar, S den der Sonne und U den des Schattens mit EU = E M =
durchschnittliche Entfernung des Mondes. Entsprechend sind P D die Tangente an die
Sonne und den Mond, die Hipparchs Modell nach näherungsweise auch durch E verläuft,
und BD die Tangente an die Sonne und die Erde bzw. den Erdschatten. Dass die Tangenten29
Er schwankt aufgrund der annähernd elliptischen Mondbahn laut heutigen Messungen etwa zwischen 57
und 63 Erdradien.
30
Vgl. TOOMER, G. J.: Hipparchus. In GILLISPIE, Charles Coulston (Hrsg.): Dictionary of scientific biography.
Band 15, Scribner, 1981, S. 213.
38
2.1. ANTIKE
U
Zweite Sprosse: Das Sonnensystem
E
S
M
P
A
B
C
D
Abb. 2.8.: Hipparchs zweite Methode zur Bestimmung der Mondentfernung („Eklipsendiagramm“).
E, M und S stellen die Mittelpunkte der Erde, des Mondes und der Sonne dar, U den des
Erdschattens in durchschnittlicher Mondentfernung.
punkte B, P und D in Wahrheit nicht genau unter den jeweiligen Mittelpunkten E, M und
S liegen, wird vernachlässigt. Mit folgender Vorgehensweise kann man nun die Entfernung
des Mondes mit der Entfernung der Sonne und dem Erdradius in Verbindung bringen:
Bei Betrachtung des Trapezes U M CA wird klar, dass UA + M C = 2EB ist, umgeformt und
mit 2,5M P für UA entsprechend
M C = 2EB − 2,5M P.
Nach Einsetzen dieser Gleichung wird aus P C = M C − M P
P C = 2EB − 3,5M P.
Aus den Dreiecken DBE und ESD, die zusammen das Trapez ESDB bilden, bekommt man
durch Anwendung des Strahlensatzes die Beziehungen
DP
DE
sodass
=
PC
EB
PC
EB
Weil S M = SE − M E, folgt
DP
und
PC
EB
=
=
DE
SM
SE
.
SE − M E
SE
39
.
=
SM
SE
,
2.1. ANTIKE
Zweite Sprosse: Das Sonnensystem
Nach einfachen Umformungen erhält man
ME =
SE(EB − P C)
EB
.
Mit dem oben berechneten P C kommt man auf
ME =
SE(3,5M P − EB)
EB
.
Mit den gewohnten Abkürzungen lautet diese Gleichung
dM =
dS (3,5rM − rE )
rE
.
Wie schon bei der ersten Methode verwendete Hipparch für den Winkeldurchmesser des
Mondes den 650sten Teil des Kreises. Dadurch lässt sich rM durch
so zu
dM =
π
dS ( 17300
d M − rE )
rE
2π dM
650 2
ersetzen und führt
.
Umgeformt erhält man die Darstellung
dM =
dS rE
7π
d
1 300 S
− rE
.
Setzt man die Sonnenentfernung von 490 Erdradien ein, ergeben sich 67,2 Erdradien für
die Mondentfernung, also fast der von Hipparch überlieferte mittlere Wert von 67 13 . Mit
Hipparchs Epizykeltheorie können auch seine zitierten Minimal- bzw. Maximaldistanzen
nachvollzogen werden.
Des Weiteren gilt: Lässt man die Sonnenentfernung immer größer werden, die geozentrische Parallaxe also kleiner, so konvergiert die Mondentfernung gegen
1 300
r.
7π E
Dies entspricht
einer Mondentfernung von 59,1 Erdradien und liegt sehr nahe am heute gemessenen mittleren Abstand von etwa 60 Erdradien. Auch Hipparch dürfte die Sonnenentfernung variiert
haben, um auf diese Tatsache zu kommen31 .
Hipparch erreichte also mit beiden Methoden die richtige Größenordnung für die Entfernung des Mondes. Mit der zweiten errechnete er sogar fast den exakten Wert. Bezüglich
der Astronomischen Einheit konnte er, außer eines Mindestbetrags, aufgrund der nicht
beobachtbaren täglichen Parallaxe keine wirklichen Fortschritte erzielen.
31
Vgl. TOOMER: Archive for History of Exact Sciences 14 [1974], S. 139f.
40
2.1. ANTIKE
Zweite Sprosse: Das Sonnensystem
2.1.3. Poseidonios
Weniger beeindruckend sind Poseidonios’ Argumente für seine Entfernungsangaben.
Bezüglich des Mondes waren seine Berechnungen ein Rückschritt zu den vorhergehenden,
weil er den Erdschatten nicht kegelförmig, sondern zylindrisch modellierte. Weiters nahm
er an, dass die Breite des Erdschattens nur doppelt so breit wie der Durchmesser des
Mondes sei, der Mondradius also gleich dem halben Erdradius. Kleomedes beschreibt die
Überlegung Poseidonius’ weiter:
„Da nun der größte Kreis der Erde nach der Berechnung des Eratosthenes
250 000 Stadien groß ist, so ist ihr Durchmesser größer als 80 000 Stadien.
Demnach würde der Durchmesser des Mondes 40 000 Stadien groß sein. Da
nun auch der Mond ähnlich der Sonne den 750sten Teil seines Bahnkreises
einnimmt, wie das Experiment der Wasseruhr zeigt, so ist der sechste Teil
der Länge dieses Kreises der Abstand des Mondes von der Erde. Dieser Abstand beträgt also 125 Monddurchmesser[32 ]. Der Monddurchmesser beträgt
aber 40 000 Stadien. Nach dieser Berechnung beträgt also die Entfernung des
Mondes von der Erde 5 000 000 Stadien.“33
Dieser Wert entspricht offensichtlich 125 Erdradien, ist also mehr als doppelt so groß wie
der tatsächliche.
Während Poseidonios zur Angabe des Sonnendurchmessers zuerst ohne Begründung
von einer Sonnenentfernung von 10 000 Erdradien ausging34 , schreibt Kleomedes später
weiter:
„Wenn wir nun die einfache Voraussetzung machen, daß die Bewegung der
Planeten mit der gleichen Geschwindigkeit erfolge, so ergibt sich, da der Mond
in 27 12 Tagen sein Bahn beschreibt, die Sonne aber in einem Jahre, daß die
Sonnenbahn 13-mal so groß ist wie die Mondbahn.“35
Mit obigem Ergebnis ergeben sich 1 625 Erdradien für die Distanz zur Sonne. Kurioserweise sollte diese, auf einer falscher Mondentfernung basierende, abgesehen von seiner
vorigen unbegründeten Abschätzung die beste bis zum Anfang des 17. Jahrhunderts bleiben. Oftmals wird Poseidonios eine noch größere Sonnenentfernung zugesprochen, die
32
Mit einfachen Worten: Die kreisrunde Mondbahn hat einen Umfang von 750 Monddurchmessern, ihr
Radius beträgt mit der Näherung von 2π ≈ 6 folglich 125 (= 750
) Monddurchmesser.
6
33
KLEOMEDES: Die Kreisbewegung der Gestirne, S. 53.
34
Vgl ibid., S. 52.
35
Ibid., S. 53.
41
2.1. ANTIKE
Zweite Sprosse: Das Sonnensystem
wahrscheinlich auf einem Schreibfehler des Geschichtsschreibers Plinius oder auf den
unplausiblen Hypothesen in einer Veröffentlichung von Friedrich Hultsch aus dem Jahre
189736 basiert37 .
2.1.4. Ptolemäus
Fast 1 400 Jahre lang dominierte das von Claudius Ptolemäus (ca. 100 – 175 n. Chr.) in
seinem Standardwerk Mathematische Zusammenstellung38 , heute unter seinem arabischen
Namen Almagest39 bekannt, beschriebene und später nach ihm benannte ptolemäische
Weltbild das astronomische Denken. Dabei handelt es sich um eine Weiterentwicklung
der geozentrischen Modelle von Apollonius und Hipparch, die die Bewegungen der Himmelskörper mit Hilfe einer komplizierten Epizykeltheorie äußerst präzise beschreibt. Diese
Theorie basiert auf der Lehre des Aristoteles, die noch auf die Pythagoreer und Platon
zurückgeht, wonach die Bewegungen der Gestirne streng geordnet, gleichmäßig und
kreisförmig sind40 . Ein Epizykel ist ein kleiner Kreis, dessen Mittelpunkt auf einem größeren die Erde umlaufenden Kreis, dem so genannten Deferenten, liegt. Der jeweilige
Himmelskörper bewegt sich also mit einer bestimmten Geschwindigkeit auf einem Epizykel, während dessen Mittelpunkt auf einem Deferenten um die Erde wandert. Durch die
entsprechende Kombination dieser beiden Dynamiken scheint sich ein Planet von der Erde
aus gesehen unregelmäßig zu bewegen: Großteils läuft er in dieselbe Richtung wie der
Epizykelmittelpunkt, in unregelmäßigen Zeitabständen jedoch gegenläufig (s. Abb. 2.9).
Schon Hipparch und Apollonius machten die Deferenten zusätzlich zu Exzentern, d. h.
ihr Mittelpunkt befindet sich etwas abseits der Erde. Dadurch kann beispielsweise erklärt
werden, warum die jährliche Bewegung der Sonne entlang der Ekliptik unterschiedlich
schnell vor sich geht (in anderen Worten: Dadurch kann beispielsweise die unterschiedliche Dauer der astronomischen Jahreszeiten begründet werden.). Um die Theorie den
beobachteten Planetenpositionen noch besser anzupassen, erfand Ptolemäus den so genannten Äquanten41 oder Ausgleichspunkt, der sich abseits des Deferentenmittelpunktes
36
HULTSCH, Friedrich: Poseidonios über die Größe und Entfernung der Sonne. Abhandlungen der Königlichen
Gesellschaft der Wissenschaften zu Göttingen, Philologisch-Historische Klasse, Neue Folge 1 1897, Nr. 5.
37
Vgl. NEUGEBAUER, Otto: A History of Ancient Mathematical Astronomy. Springer, 1975, S. 655ff.
38
gr. MAΘEMATIKE ΣΥNTAΞIS (mathematike syntaxis)
39
Spätere Abschriften des hoch angesehenen Werkes trugen den Titel Größte Zusammenstellung (Megiste
Syntaxis), was als al-majastı̄ in die arabischen Übersetzungen übernommen wurde und von dort als
Almagest in den heutigen Sprachgebrauch überging.
40
Für die Pythagoreer war der Grund für die als vollkommen und unvergänglich angesehene
Kreisbewegeung die Göttlichkeit der Gestirne. Platon argumentierte umgekehrt: Weil sich die
Himmelskörper nach mathematischen Regeln bewegen, müssen sie beseelt und göttlich sein.
41
lat. punctum aequans
42
2.1. ANTIKE
Zweite Sprosse: Das Sonnensystem
Planetenbahn
Erde
Deferentenmittelpunkt
Abb. 2.9.: Erklärung der rückläufigen Planetenbewegung mit Hilfe des Epizykelmodells
und der Erde befindet und von dem aus gesehen die Bewegung eines Epizykelmittelpunktes
gleichförmig erscheint (s. Abb. 2.10). Dieser und weitere Kunstgriffe (insbesondere sich
drehende Exzenter bei Mond und Merkur) verkomplizierten das Modell jedoch erheblich42 .
Die Entfernungen von Mond und Sonne
Im Almagest ging es Ptolemäus nicht darum, Entfernungen von Himmelskörpern zu bestimmen, sondern ihre Positionen vorherzusagen. Für Planeten spielen ihre Entfernungen dafür
keine Rolle, sehr wohl jedoch für den Mond, der eine nicht vernachlässigbare geozentrische
Parallaxe hat, die, wie schon erwähnt, für die Zeit und den Ort einer Sonnenfinsternis
entscheidend ist. Deshalb müssen Beobachtungsergebnisse auf den Erdmittelpunkt umgerechnet werden. Da die Bewegung des Mondes, wie wir heute wissen, stark von der Sonne
beeinflusst wird, ist eine einfache mathematische Modellierung nicht möglich. Ptolemäus
erreichte mit einem komplizierten Epizykelmodell mit beweglichem Exzenter lediglich eine
gute Übereinstimmung in den Syzygien (Sammelbegriff für Opposition und Konjunktion
von Mond und Sonne, d. h. bei Voll- oder Neumond) und Quadraturen (d. h. im ersten
oder letzten Viertel bzw. bei zunehmendem oder abnehmendem Halbmond). Mit diesem
Modell konnte er das Verhältnis zwischen mittlerer Entfernung in den Syzygien und den
Quadraturen mit 60 zu 39 11
angeben.
30
42
Vgl. DIJKSTERHUIS, E. J.: Die Mechanisierung des Weltbildes. Springer, 1956, S. 66f.
43
2.1. ANTIKE
Zweite Sprosse: Das Sonnensystem
A
Planet
E
De
fe
ren
t
Epizykel
Erde
D
Äquant
Abb. 2.10.: Epizykelmodell mit einem exzentrischen Deferenten und Ausgleichspunkt. Der Epizykelmittelpunkt E durchläuft den Exzenter so, dass seine Bewegung nicht vom Deferentenmittelpunkt D, sondern vom Äquanten aus gesehen gleichförmig erscheint, d. h. der
Punkt A bewegt sich mit konstanter Winkelgeschwindigkeit auf dem Ausgleichskreis
und erfüllt somit das Axiom der gleichförmigen Kreisbewegung.
Ptolemäus bezog seine Entfernungsangaben zunächst immer auf eine ausgewählte Strecke, der er 60 Teile
zuordnete und rechnete erst zum Schluss in tatsächliche Distanzen um. Weiters gab er Brüche bzw. Nachkommastellen nicht in gekürzter Form an, sondern, so wie wir immer noch bei Winkeln die Bogenminuten und
-sekunden, in Sexagesimalform (lat. sexagesimus „der sechszigste“) zur Basis 60; also beispielsweise 3 80 3000
für π (3 +
8
60
+
30
602
17
= 3 120
≈ 3,14166)43 , oder folgendermaßen in seinen Sehnentafeln44 (ausgehend von
einem Kreis mit Radius von 60 Längeneinheiten):
chord(90◦ ) = 84p 510 1000 ,
was soviel bedeutet wie 84 +
p
60 · 2 ≈ 84,8528 entspricht.
51
60
+
10
602
Teile (lat. partes) und sehr genau dem tatsächlichen Wert von
Um absolute Angaben zu erlangen, verglich er die in Alexandria gemessene Mondposition
mit der bezüglich des Erdmittelpunktes berechneten und kam auf einen Parallaxenwinkel
von 1◦ 70 (umgerechnet in die horizontale Parallaxe: 1◦ 260 ). Daraus berechnete er eine
geozentrische Mondentfernung von 39 34 Erdradien zum Zeitpunkt der Beobachtung, die
5
seinen Berechnungen zufolge 40 12
von 60 Teilen entsprach. Daher transformiert der Faktor
43
PTOLEMÄUS, Claudius; MANITIUS, Karl (Hrsg.): Handbuch der Astronomie. Band 1, Teubner, 1963, VI: 7;
S 384.
44
Ibid., I: 11; S. 37ff.
44
2.1. ANTIKE
39 34
5
40 12
=
477
485
Zweite Sprosse: Das Sonnensystem
alle relativen Abstände in absolute, nämlich ziemlich genau 59 Erdradien für
den mittleren Abstand in den Syzygien und 38 43
Erdradien in den Quadraturen45 .
60
Dass mit dem von ihm angegebenen Wert von 5 16 46 Erdradien für den Epizyklenradius
der Mond bei seiner Minimalentfernung in einer Quadratur mit 33 11
(= 38 43
− 5 16 )
20
60
Erdradien fast doppelt so groß erscheinen müsste wie bei seiner Maximalentfernung in
einem Syzygium mit 64 16 (= 59 + 5 16 ) Erdradien, muss Ptolemäus bewusst gewesen sein,
auch wenn er diese Tatsache nicht kommentierte. Nach seinen Ergebnissen schreibt er
weiter:
„Nachdem von uns auf die dargelegte Weise die Entfernungen des Mondes
nachgewiesen worden sind, dürfte es der Reihenfolge nach die nächste Aufgabe
sein, auch die Entfernung der Sonne mit nachzuweisen, da auch diese Aufgabe
auf dem Wege der geometrischen Konstruktion bequem zu lösen ist, wenn
außer den Entfernungen des Mondes in den Syzygien noch die Größen der
Winkel gegeben sind, unter welchen die Durchmesser der Sonne, des Mondes
und des (Erd-) Schattens in den Syzygien dem Auge erscheinen.“47
Ptolemäus verwendete also wie schon Hipparch das Eklipsendiagramm für die Entfernungsbestimmung der Sonne, allerdings war seine Vorgangsweise der von Hipparch gerade
entgegengesetzt. Er nahm an, dass der Winkeldurchmesser der Sonne nahezu konstant
(„... d. h. ein beträchtlicher Unterschied infolge ihrer (verschiedenen) Entfernungen tritt
nicht ein.“48 ) und gleich dem des Mondes bei seinem Maximalabstand zur Erde erscheint,
nämlich zu 310 2000 (entspricht dem 689,36sten Teil des Kreises), während der Durchmesser
des Schattens nahezu das 2 35 -fache betrage49 . Diese Werte führen mit Hipparchs Vorgehensweise bzw. nach Umformen der Formel auf S. 40 (weil die Funktion dM (dS ) symmetrisch
zur ersten Mediane ist, muss man nur die Indizes vertauschen) auf die Gleichung
dS =
d M rE
7,2π
d
1378,72 M
− rE
und mit dM = 64 16 somit auf eine Sonnenentfernung von 1 217 Erdradien50 . Im darauf
folgenden Kapitel bestimmte Ptolemäus noch den Sonnenradius zu 5 12 Erdradien51 . Im
45
Vgl. PTOLEMÄUS: Handbuch der Astronomie 1, V: 13; S. 301 – 304.
Ibid., V: 13; S. 304.
47
Ibid., Almagest V: 13; S. 305.
48
Ibid., Almagest V: 14; S. 305.
49
Vgl. ibid., Almagest V: 14; S. 309.
50
Ptolemäus gibt wegen Rundungsfehlern 1 210 Erdradien an.
51
Ibid., Almagest V: 16; S. 313.
46
45
2.1. ANTIKE
Zweite Sprosse: Das Sonnensystem
Almagest führte er aber nirgends an, welcher Stelle der Sonnenumlaufbahn die genannte
Entfernung entspricht, weil das für seine Eklipsenberechnungen nicht entscheidend war.
Erst in seinen Planetarischen Hypothesen (s. u.) ordnete er die 1 210 Erdradien der mittleren
Sonnendistanz zu und gab mit Hilfe der Exzentrizität der Sonnenbahn für den Minimalabstand der Sonne 1 160 Erdradien und für den Maximalabstand 1 260 Erdradien an. In
Wahrheit betragen die mittlere Sonnendistanz und ihr Radius aber fast das 20-fache. Da die
verwendete Mondentfernung, sein Winkeldurchmesser und die Erdschattenbreite aber nur
geringfügig von den tatsächlichen Werten abweichen, bedeutet das, dass die Lösung von
Ptolemäus im Gegensatz zu der Vorgangsweise von Hipparch sehr empfindlich gegenüber
Änderungen der Messdaten ist. Deshalb verdient Hipparchs Methode wissenschaftlich
gesehen auch mehr Anerkennung. Außerdem wird Ptolemäus heute oft vorgeworfen, er
hätte seine Messungen den Ergebnissen angeglichen52 . Ein Hinweis dafür ist, dass seine
berechnete Astronomische Einheit entsprechend der Behauptung von Aristarch ziemlich genau das 19-fache der Mondentfernung beträgt. Lange Zeit wurde dies jedoch als Argument
für die Richtigkeit beider Resultate angesehen.
Die Entfernungen der Planeten
Die Entfernungen der Planeten behandelte Ptolemäus nicht im Almagest, sondern in
seinem späteren Werk Planetarische Hypothesen53 . Wie bei der Berechnung der Mondentfernung, ging er von den Abstandsverhältnissen aus, die ihm seine Epizykelmodelle
lieferten. Um diese in Verbindung zu bringen und zu absoluten Entfernungen zu machen,
verwendete er die Behauptung von Aristoteles, wonach es keinen leeren Raum gebe, sodass
die Planetensphären dicht aneinander liegen müssen. Demnach ist die Maximaldistanz
eines Planeten gleich der Minimaldistanz des nächst folgenden (s. Abb. 2.11).
Um zwischen Mond und Sonne keinen leeren Raum vorherzusagen, setzte Ptolemäus
die Sphären von Merkur und Venus dorthin. Merkur nur deswegen näher zur Erde, weil
seine Bewegung, ebenso wie die des Mondes, komplizierter erschien und er annahm, dass
nebeneinander liegende Bahnen sich ähneln. Beginnend mit dem Minimalabstand von
Merkur, der gleich dem Maximalabstand des Mondes war, errechnete er mit Hilfe seiner
Entfernungsverhältnisse seinen Maximalabstand, der dann dem Minimalabstand der Venus
entsprach. Dass der analog berechnete Maximalabstand der Venus aber nicht genau der
oben genannte minimale Sonnenabstand war, kommentierte Ptolemäus folgendermaßen:
52
Vgl. NEWTON, Robert R.: The crime of Claudius Ptolemy. Johns Hopkins Univ. Press, 1977.
gr. ΥΠOΘEΣEΩN TΩN ΠΛANΩMENΩN (hypotheseon ton planomenon)
54
Als Opposition bezeichnet man in der Astronomie diejenige Konstellation, bei der sich zwei Himmelskörper
am Himmel 180◦ gegenüberstehen. Interessant sind im Regelfall nur Oppositionen zur Sonne. Im Gegensatz
dazu spricht man von einer Konjunktion, wenn sich zwei Himmelskörper in derselben Richtung befinden.
53
46
2.1. ANTIKE
Zweite Sprosse: Das Sonnensystem
Fixsterne
Saturn
Merkur
Mond
Erde
Sonne
Jupiter
Venus
Mars
Abb. 2.11.: Die Planetenbahnen nach Ptolemäus. Die gestrichelten Linien stellen die Maximal- bzw.
Minimalentfernung des jeweiligen Himmelskörpers dar. Die nicht gestrichelten Kreise
sind die Epizyklen, die grauen exzentrischen Ringe kennzeichnen den Bereich, in dem
sich der Himmelskörper bewegt. Die eigentlichen Exzenter, die sich in der Mitte der
Ringe befänden, sind der Übersicht halber nicht eingezeichnet. Ganz außen ist die
Fixsternsphäre skizziert, gefolgt von der Saturn-, Jupiter-, Mars- und Sonnensphäre,
die ohne Epizykel auskommt. Innerhalb der Sonnensphäre kann man noch die Sphäre
und den Epizykel der Venus erkennen. Merkur, Mond und Erde sind nur mehr in einem
schwarzen Punkt abgebildet.
Auffällig ist noch, dass die Verbindungslinien zwischen den „oberen“ Planeten Mars,
Jupiter und Saturn und ihren jeweiligen Epizykelmittelpunkten alle parallel zur Verbindungslinie Erde–Sonne sind, d. h. bei allen dauert ein Epizykelumlauf genau 1 Jahr.
Der Grund dafür ist, dass die rückläufige Bewegung dieser drei Planeten immer nur in
Opposition54 zur Sonne stattfindet.
47
2.1. ANTIKE
Zweite Sprosse: Das Sonnensystem
„Da die kleinste Entfernung der Sonne, wie wir erwähnt haben, 1 160 Erdradien
beträgt, ist eine Unstimmigkeit zwischen den zwei Distanzen, die wir nicht
erklären können; aber wir wurden unausweichlich zu den Entfernungen geführt, die wir niedergeschrieben haben. Erst recht für die zwei (planetarischen)
Sphären, die näher zur Erde liegen, als die anderen. Die übrigen Sphären
können nicht zwischen der Sphäre des Mondes und der Sonne liegen, denn
schon die Sphäre des Mars, die die erdnächste der verbleibenden Sphären ist,
und deren Verhältnis der größten zur kleinsten Distanz etwa 7:1 ist, kann nicht
zwischen die größte Entfernung der Venus und die kleinste Entfernung der
Sonne untergebracht werden. Andererseits ist es so, dass wir, wenn wir den
Mondabstand vergrößern, gezwungen sind, den Sonnenabstand zu verringern,
und vice versa. Wenn wir daher den Mondabstand [im Eklipsendiagramm im
Almagest] ein wenig vergrößern, wird der Sonnenabstand ein bisschen geringer
sein und wird dann mit der Maximalentfernung der Venus übereinstimmen.“55
Ptolemäus selbst führte diese Anpassung nicht durch. Die Distanzen von Mars, Jupiter
und Saturn ließen sich wiederum einfach von der Maximalentfernung der Sonne ableiten.
Zusätzlich schätzte Ptolemäus noch die Winkeldurchmesser der Planeten bei mittlerer
Entfernung im Vergleich zum Sonnendurchmesser ab, ohne seine Vorgangsweise dafür
zur erklären, und berechnete daraus mit Hilfe des wahren Sonnendurchmessers, der im
Almagest zu 5 12 Erdradien bestimmt wurde (s. o.), ihre wahren Größen. Alle Ergebnisse
sind in Tabelle 2.2 zusammengefasst56 .
33
1 160
Mond
48
64
Merkur
115
166
Venus
622,5
4
3
1
15
1
10
0,29
0,04
0,3
Sonne
1 210
1
5,5
1 260
Mars
5 040
8 820
Jupiter
11 504
1 079
14 187
Saturn
17 026
1
20
1
12
1
18
1,14
4,36
4,3
19 865
Fixsterne
≈20 00057
1
bis 30
4,55 bis 3,03
1
20
Tab. 2.2.: Ptolemäus’ Ergebnisse. Jeweils die Mindest-, Durchschnitts- und Maximalentfernung
(in Erdradien), die wiederum der Mindestentfernung des nächsten Himmelskörpers
entspricht. Unter den mittleren Distanzen sind die von Ptolemäus abgeschätzten Winkeldurchmesser der Himmelskörper relativ zur Sonne und die daraus resultierenden
absoluten Durchmesser im Vergleich zur Erde angegeben.
55
Frei übersetzt nach PTOLEMÄUS, Claudius; GOLDSTEIN, Bernard R. (Hrsg.): The Arabic Version of Ptolemy’s
Planetary Hypotheses. American Philosophical Society, 1967, S. 7 (Originaltext im Anhang).
56
Vgl. NEUGEBAUER: A History of Ancient Mathematical Astronomy, S. 920ff.
57
Abschätzung von Ptolemäus
48
2.2. MITTELALTER
Zweite Sprosse: Das Sonnensystem
Letztendlich kann man sagen, dass der richtige Abstand des Mondes in der Antike
schon annähernd bekannt war, während alle anderen Angaben entweder die Folge von
unvermeidbaren Messfehlern waren oder überhaupt nur auf Spekulationen beruhten.
Dennoch wurden sie kaum angezweifelt und sollten erst Jahrhunderte später verbessert
werden.
2.2. Mittelalter
Wie die meisten wissenschaftlichen Errungenschaften der Antike, wurden auch die Werke
von Ptolemäus vorrangig von islamischen Gelehrten bewahrt und als arabische Übersetzungen überliefert. Zu den wichtigsten zählen Al Farghānı̄ (ca. 800 – 870), Al Battānı̄ (ca.
850 – 929) und Al Bı̄rūnı̄ (973 – 1048). Dabei wurde das Sphärenmodell von Ptolemäus
und somit auch die Entfernungen zu den Himmelskörpern nur geringfügig abgeändert
und verbessert (etwa durch die von ihm versäumten Anpassungen zur Vermeidung der
Unstimmigkeit zwischen Venus- und Sonnensphäre, durch Vergrößerung der Sphären um
den Durchmesser der Planeten oder durch Anhängen eines weitere Epizykels). Es wurde aber auch Kritik geübt, insbesondere an der Methode des Ausgleichspunktes, der am
ehesten die Forderung nach gleichförmigen Kreisbewegungen zu missachten schien (Al
Tūsı̄ gelang durch Einführung eines Epizykelpaars eine Alternative zum Äquanten, auf die
später auch Kopernikus zurückgriff); oder wegen der schon erwähnten Tatsache, dass die
Himmelskörper im Laufe der Zeit unterschiedlich groß erscheinen müssten. Beispielsweise
der Mond oder die Venus, die mit im vorhergehenden Abschnitt genannten Daten in ihrem
Perigäum58 einen Winkeldurchmesser von fast
2
5
von dem der Sonne haben müsste. Das
Sphärenmodell selbst und viele teils noch von Hipparch stammende ungenaue Messdaten
wurden jedoch nicht angezweifelt.
Im 11. Jahrhundert gelangte die ptolemäische Astronomie inklusive ihrer Größenordnung
allmählich ins Abendland und verschmolz zusammen mit der aristotelischen Philosophie
und dem jüdisch-christlichen Denken, nicht zuletzt durch die Werke von Thomas von
Aquin (ca. 1225 – 1274) und Dante Alighieri (1265 – 1321), zu einem allseits anerkannten Weltbild. Dennoch war die Vorstellung, dass dieses Modell falsch sein könnte, dem
europäischen Denken nicht gänzlich fremd. In einem Kommentar zu Aristoteles’ Werk Über
58
gr. περί (perí) „nahe“, γαι̃α (gaĩa) „Erde“; „erdnächste Punkt“. Vgl. Perihel: ήλιoς (helios) „Sonne“;
„sonnennächste Punkt“. Im Gegensatz dazu Apogäum/Aphel: άπo (ápo) „weg von“;
„erdfernste/sonnenfernste Punkt“.
49
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
das Himmelsgewölbe schrieb der französische Geistliche und Naturwissenschaftler Nikolaus
Oresme (ca. 1320 – 1382):
„Deshalb sage ich: Wenn der höhere (oder himmlische) Teil der beiden Teile
des Weltalls ... heute eine tägliche Bewegung erführe, wie es der Fall ist,
während der untere (oder irdische) Teil in Ruhe verbleibt; und wenn morgen
dagegen der untere Teil eine tägliche Bewegung erführe, während der andere
Teil, nämlich der Himmel, in Ruhe verweilte, so wären wir nicht imstande,
irgendeine Veränderung zu erkennen; vielmehr würde alles heute und morgen
gleich zu sein scheinen. Wir würden durchweg meinen, unser Ort wäre im
Ruhezustand, wogegen sich der andere Teil des Weltalls bewegte, ebenso wie
ein Mann in einem fahrenden Boot den Eindruck hat, daß sich die Bäume
draußen bewegen.“59
Er stellte aber klar, dass er nicht an die Bewegung der Erde glaube.
Auch der Universalgelehrte Nikolaus von Kues (1401 – 1464), Cusanus genannt, behauptete, dass die Erde nicht unbewegt im Zentrum des Universums ruhe. Ein alternatives
Modell stellte er jedoch nicht vor. Das gelang erst Nikolaus Kopernikus.
2.3. Neuzeit
2.3.1. Kopernikus
Nikolaus Kopernikus60 (1473 – 1543) wurde aufgrund seiner Theorien von der Bewegung
der Planeten um die Sonne zu einem der bedeutendsten Astronomen des Abendlandes.
Durch Aristarchs Schriften inspiriert, war er davon überzeugt, mit folgenden Annahmen
das Universum weitaus einfacher als Ptolemäus beschreiben zu können:
1. „Der Mittelpunkt aller Himmelskreise oder -kugeln ist nicht ein einziger.“
2. „Der Mittelpunkt der Erde ist nicht die Weltmitte, sondern nur der von
der Schwere und Mondkreis.“
3. „Alle Kreise laufen um die Sonne, als stünde sie in der Mitte von allen,
und deshalb liegt der Weltmittelpunkt nahe bei der Sonne.“
59
LOVELL, Barnard: Das unendliche Weltall – Geschichte der Kosmologie von der Antike bis zur Gegenwart.
dtv, 1988, S. 31, aus Oresme: Le livre du ciel et du monde.
60
In seinen Veröffentlichungen findet man eigentlich die Schreibweise Nicolaus Copernicus. Wegen seiner
deutsch-polnischen Wurzeln ist auch sein nicht-latinisierter Name strittig: Nikolas Koppernigk oder Mikołaj
Kopernik.
50
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
4. „Das Verhältnis der Sonnen-Erd-Entfernung zur Höhe des festen Himmels
ist kleiner als das zwischen Erdhalbmesser und Sonnenentfernung, so
sehr, daß sie im Verhältnis zur Höhe des festen Himmels unmerklich
ist. Alles, was infolge von Bewegung am Himmel erscheint, rührt nicht
von dorther, sondern liegt an der Erde. Die Erde also ist es, die sich mit
den Stoffen in ihrer Nähe in einer Tages-Bewegung einmal ganz in ihren
unveränderlichen Angelpunkten um sich dreht, wohingegen der feste,
oberste Himmel unbeweglich bleibt.“
5. „Alles, was uns infolge von Bewegungen an der Sonne erscheint, kommt
nicht von dieser selbst her, sondern ist von der Erde und unserem Umlauf
verursacht, mittels dessen wir uns um die Sonne drehen, vergleichbar
irgendeinem anderen Gestirn; so führt die Erde mehrere Bewegungen
aus.“
6. „Was an Rücklauf und Vorlauf an den Planeten erscheint, rührt nicht von
denen selbst her, sondern von der Erde. Bewegung von ihr allein reicht also
zur Erklärung für so viele am Himmel erscheinende Ungleichmäßigkeiten
aus.“
„Dies so vorangestellt, werde ich versuchen, kurz aufzuzeigen, wie sauber die
Gleichförmigkeit der Bewegungen gewahrt werden kann. Dabei meinte ich, der
Kürze wegen mathematische Beweisgänge fortlassen zu sollen, – die sind für
einen größeren Band bestimmt.“61
Dieser größere Band erschien in seinem Todesjahr unter dem Titel Von den Umdrehungen
der Himmelskörper62 . Darin stellte er ein detailliertes Weltbild dar, das zwar die Planeten
und insbesondere die Erde um die Sonne kreisen ließ und ohne die fraglichen Äquanten
auskam, jedoch immer noch dem Axiom der gleichförmigen Kreisbewegungen unterlag
und deshalb mit Epizykeln funktionierte. Für die Erklärung der rückläufigen Bewegungen
wären diese eigentlich nicht mehr notwendig gewesen (s. Abb. 2.12), aber Kopernikus
ersetzte, angeregt von arabischen Schriften, die Äquanten und für die Erde auch den
Exzenter durch aufeinander gesetzte Epizykel (genauer gesagt: Im Zentrum seines Weltbildes befand sich der Mittelpunkt der kreisrunden Erdbahn, die so genannte mittlere
Sonne. Dieser ausgezeichnete Punkt stellte einerseits auch den Mittelpunkt für eine kleine
Deferenten-Epizykel-Kombination für die Sonne, andererseits den fixen Bezugspunkt für
61
COPERNICUS, Nicolaus; ZEKL, Hans Günter (Hrsg.): Das neue Weltbild. Meiner, 1990, COMMENTARIOLUS
S. 5ff.
62
lat. DE REVOLUTIONIBUS ORBIUM COELESTIUM
51
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
5
5
4
2
3
4
3
2
1
1
Abb. 2.12.: Erklärung der rückläufigen Planetenbewegung mit Hilfe des heliozentrischen Modells
die exzentrischen Deferenten der übrigen Planeten dar)63 . Daher benötigte sein Modell für
ähnlich genaue Vorhersagen schlussendlich sogar mehr Epizykel als das des Ptolemäus.
Im Gegensatz zum ptolemäischen Weltbild baute die Reihenfolge der so genannten inneren Planeten Merkur und Venus nicht mehr auf Spekulation und Konvention auf, sondern
auf ihren maximalen Elongationen. Auch die relativen Entfernungen der Planeten basierten
nicht auf den dicht aneinander liegenden Sphären, sondern konnten folgendermaßen
berechnet werden64 :
Näherungsweise wird vorerst von konzentrischen kreisförmigen Planetenbahnen um die
Sonne ausgegangen. Abbildung 2.13 zeigt anhand von Venus und Mars, wie die Parameter
des geozentrischen Epizykelmodells von Ptolemäus für innere und äußere Planeten im
heliozentrischen Modell von Kopernikus verwendet werden können.
Die Verhältnisse der Deferentenradien zu den Epizykelradien betragen laut Almagest
E Z 0 : Z 0 V 0 = 60 : 43 16 für Venus65 bzw. E 0 Z 0 : Z 0 M 0 = 60 : 39 12 für Mars66 . Bei jeder Elonga0
tion α und β, die unabhängig vom Modell sind, gelangt man über ähnliche Dreiecke auf
63
Vgl. KUHN, Thomas S.: The Copernican Revolution – Planetary Astronomy in the Development of Western
Thought. Harvard University Press, 1957, S. 168ff.
64
Vgl. NEUGEBAUER: A History of Ancient Mathematical Astronomy, S. 146.
65
Vgl. PTOLEMÄUS, Claudius; MANITIUS, Karl (Hrsg.): Handbuch der Astronomie. Band 2, Teubner, 1963,
Almagest X: 2; S. 161.
66
Vgl. ibid., Almagest X: 8; S. 198.
52
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
geozentrisch
heliozentrisch
V
V’
E’
Venus
a
E
S’
a
S
Z’
M’
Z’
M
S’
b
Mars
S
E’
b
E
Abb. 2.13.: Berechnung der Planetenentfernungen von Venus und Mars nach Kopernikus mit Hilfe
des geozentrischen Epizykelmodells nach Ptolemäus. Weil 4E 0 Z 0 V 0 und 4ESV bzw.
4E 0 Z 0 M 0 und 4M S E zueinander ähnlich sind, kann man aus den Verhältnissen der
Deferentenradien zu den Epizykelradien leicht die Entfernungen der Planeten zur Sonne
(in AE) angeben.
~
M
V’
E’ a
M
~
E
b
E
S’
Venus
S
Mars
Abb. 2.14.: Direkte Berechnung der Planetenentfernungen von Venus und Mars nach Kopernikus.
Mit Hilfe der dargestellten Planetenkonstellationen (wenn Mars sich in Opposition
befindet bzw. die Winkel EV S und S E M rechte sind, die Elongation der Venus also
maximal ist bzw. der Mars sich in Quadratur befindet) lassen sich die Entfernungen der
Planeten zur Sonne (in AE) auch ohne Verwendung der Epizykel- und Deferentenradien
angeben.
53
2.3. NEUZEIT
die einfachen Beziehungen
Zweite Sprosse: Das Sonnensystem
E0 Z 0
Z0V 0
=
ES
SV
bzw.
E0 Z 0
Z0M0
=
MS
.
SE
Daher lassen sich die Entfernungen
0
SV und M S auf einfache Weise mit der Astronomischen Einheit in Relation bringen:
SV =
MS =
Z 0V 0
E0 Z 0
ES
E0 Z 0
Z0M0
SE
Die Abstände der übrigen Planten zur Sonne verhalten sich analog.
Eine direktere Vorgehensweise ohne die Verwendung der Epizykel- und Deferentenradien
(bzw. wurden diese von Ptolemäus auf ähnliche Weise bestimmt) ist folgende67 :
• Für innere Planeten: Wenn die Elongation α maximal68 ist, wie in Abbildung 2.14
angedeutet, ist EV eine Tangente auf die Venusbahn und steht folglich normal auf
den Radius SV . Daraus ergibt sich der einfache Zusammenhang
SV = ES sin α.
• Für äußere Planeten ist die Vorgehensweise etwas komplexer: Hier geht man von
einem Zeitpunkt aus, zu dem Mars in Opposition zur Sonne steht (in Abb. 2.14 M̃ ).
Da sich die Erde schneller um die Sonne bewegt als die äußeren Planeten, tritt
nach einiger Zeit die Situation ein, dass die Elongation β ein rechter Winkel ist. Mit
Hilfe des Verhältnisses der vergangenen Zeit seit der Opposition zur Umlaufzeit des
Planeten um die Sonne lassen sich nun die Winkel ES Ẽ und M S M̃ berechnen.
Daraus folgt durch Subtraktion der Winkel ESM und weiter das gesuchte Ergebnis
MS =
ES
cos ESM
.
Wiederum verhalten sich die Abstände der anderen Planeten analog.
Da sich die Planeten auch im kopernikanischen Modell auf exzentrischen Deferenten
und Epizykeln bewegen, handelt es sich bei den resultierenden Werten um die mittleren
Abstände zur mittleren Sonne, also dem Mittelpunkt der kreisförmigen Erdbahn. Die
maximalen bzw. minimalen Entfernungen ergeben sich durch Addieren bzw. Subtrahieren
der Exzentrizitäten und Epizykelradien.
67
68
Vgl. KUHN: The Copernican Revolution, S. 175.
Der Wert für die maximale Elongation schwankt je nach Erdnähe; s. Abb. 2.15.
54
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
E
A
F
B
C D
Abb. 2.15.: Messung der „größt- und kleinstmöglichen maximalen Elongationen“ eines inneren
Planeten. C stellt den Mittelpunkt der Erdbahn dar, also gleichzeitig die mittlere Sonne,
D den Mittelpunkt der Bahn des inneren Planeten, die ebenfalls als Kreis ohne Epizykel
vereinfacht wird. A und B sind die fernsten bzw. nächsten Positionen der Erde zur
Bahn des Planeten. E und F sind die jeweiligen Stellungen des Planeten mit maximaler
Elongation.
Für die inneren Planeten lässt sich die Berechnung der maximalen und minimalen Abstände von der mittleren Sonne auch durch die Bestimmung der „größt- und kleinstmöglichen
maximalen Elongationen“ (s. Abb. 2.15) nachvollziehen. Dazu muss die Elongation über
viele Jahre hinweg gemessen werden. Die „größtmögliche maximale Elongation“ DBF
liegt dann vor, wenn die Erde der Bahn des inneren Planeten am nächsten kommt (B). Zur
„kleinstmögliche maximale Elongation“ DAE kann es daher nur dann kommen, wenn
Erde am weitesten von der Planetenbahn weg ist (A), also nur ein halbes Jahr vor bzw.
nach der vorher beschriebenen Situation.
Weil AE D und BF D rechte Winkel sind, ergibt sich folgendes:
DE = AD sin DAE
und
Aus DE = DF folgt BD =
und daher AB = AD + BD = (1 +
also AD =
DF = BD sin DBF.
sin DAE
sin DBF
sin DAE
sin DBF
2
AC
sin DAE
1 + sin DBF
55
AD
)AD = 2AC,
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
und deshalb für die Abweichung vom mittleren Abstand zum Zentrum der Erdbahn
C D = AD − AC = (
2
1+
sin DAE
sin DBF
− 1)AC.
DE = DF ausgedrückt durch AC ergibt DE =
sin DAE
AC.
sin DAE
1
(1
+
)
2
sin DBF
◦
Für die Winkel DAE und DBF verwendete Kopernikus die Werte 44 45 und 47 13
◦ 69
, die
für minimalen, mittleren und maximalen Abstand zum Mittelpunkt der Erdumlaufbahn die
Werte 0,70 AE, 0,72 AE und 0,74 AE ergeben.
In Tabelle 2.3 sind die Ergebnisse von Kopernikus, die ziemlich genau modernen Messungen entsprechen, zusammengefasst70 71 und in Abbildung 2.16 skizziert.
Tab. 2.3.: Kopernikus’ Ergebnisse für die mittleren Entfernungen der Planeten zur mittleren Sonne
bzw. der Erde zur wahren Sonne in AE (inkl. Maximal-/Minimalabstand, ± beschreibt
also nicht den Fehler!).
Merkur
0,38 ± 0,12
Venus
0,72 ± 0,02
Erde
1,00 ± 0,03
Mars
1,52 ± 0,15
Jupiter
5,22 ± 0,24
Saturn
9,1772 ± 0,52
Der Mond scheint in dieser Tabelle nicht auf, weil er sich ja auch im kopernikanischen
Weltbild um die Erde bewegt. Bezüglich seiner Bahn konnte Kopernikus, wenn auch nur
mit derselben Vorgehensweise wie Ptolemäus (mit Hilfe seiner horizontalen Parallaxe),
erhebliche Verbesserungen erzielen. Sein Modell sagt dem Mond in den Quadraturen
eine Maximal- bzw. Minimalentfernung von 68 13 bzw. 52 17
Erdradien zur Erde vorher,
60
8
in den Syzygien 65 12 bzw. 55 60
– also Entfernungen, die keine so massiven scheinbaren
Größenänderungen wie bei Ptolemäus zur Folge haben und sehr nahe an den tatsächlichen
Werten liegen73 .
Um die relativen Abstände der Planeten in absolute umzuwandeln, benötigte Kopernikus
jedoch den tatsächlichen Wert der Astronomischen Einheit oder die wahre Distanz zu einem
Planeten. Da zu jener Zeit eine geozentrische Parallaxenmessung jedoch noch für keine der
beiden Optionen möglich war, blieben auch Kopernikus nur die alt bekannten Methoden
der Monddichotomie oder des Eklipsendiagramms zur Ermittlung des Sonnenabstands.
69
Vgl. PTOLEMÄUS: Handbuch der Astronomie 2, Almagest X: 2; S. 159.
Vgl. ibid., Almagest IX: 9, X: 2, 8, XI: 2, 6; S. 144, 161, 198, 223, 247.
71
Vgl. COPERNICUS, Nicolaus: De revolutionibus orbium coelestium. Johannes Petreius, 1543, V: 9, 14, 19, 21,
27.
72
Mit dem Wert aus dem Almagest: 9,23.
73
Vgl. ibid., IV: 16, 17.
70
56
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
Saturn
Jupiter
Mars
Abb. 2.16.: Die Planetenbahnen nach Kopernikus. Die grauen Ringe kennzeichnen den Bereich, in
dem sich die jeweiligen Planeten bewegen.
Er entschied sich wie Ptolemäus für letztere Methode, wobei er mit leicht abgeänderten
Messdaten auf eine Entfernung von 1 179 Erdradien im Apogäum und mit seinem Wert
für die Exzentrizität auf eine mittlere Entfernung von 1 142 Erdradien kam74 , passend zu
einer horizontalen Parallaxe von ziemlich genau 30 . Dies entspricht wiederum etwa dem
19-fachen Mondabstand und somit nicht einmal einem Zwanzigstel des tatsächlichen Werts.
Eingesetzt in die Planetenabstände erkennt man, dass die Ausmaße des Sonnensystems
im kopernikanischen Modell im Vergleich zum ptolemäischen stark geschrumpft sind: Bei
Kopernikus beträgt der Radius der Umlaufbahn des äußersten Planeten im Mittel 10 472,
bei Ptolemäus noch 17 026 Erdradien.
Für die Fixsterne hingegen sagt das heliozentrische Modell, wie schon in der vierten
Annahme Kopernikus’ angedeutet, eine immense Entfernung voraus, weil trotz der großen
Basislinie von 2 AE, die einem Beobachter auf der Erde innerhalb eines halben Jahres zur
Verfügung steht, keine Sternparallaxen gemessen wurden (s. Abb. 2.17).
74
Vgl. COPERNICUS: De revolutionibus, IV: 19.
57
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
Fixsterne
Sonne
Erdbahn
Abb. 2.17.: Sternparallaxe im Modell der Fixsternsphäre. Die Position jedes Sterns bzw. der Winkel
zwischen zwei Sternen müsste sich innerhalb eines halben Jahres leicht ändern. Beispielsweise müssten Sterne, die einander zu einer bestimmten Zeit gegenüberliegen,
ein halbes Jahr später einen von 180◦ verschiedenen Winkel einschließen. Eine solche
Abweichung konnte jedoch bis ins 19. Jahrhundert nicht gefunden werden.
Da das kopernikanische Modell weder entscheidend einfacher noch genauer als das
ptolemäische war, hatte es anfangs wenig Anhänger und folglich auch wenig Kritiker, nicht
einmal seitens der Kirche.
2.3.2. Tycho und Kepler
Auch der dänische Astronom Tycho Brahe (1546 – 1601), meist nur Tycho genannt und
berühmt wegen der Entdeckung einer Supernova, der Beobachtung eines Kometen und
vor allem äußerst exakter Beobachtungen der Gestirne mit einer Genauigkeit von bis
zu 10 , konnte weder eine Sternparallaxe übers Jahr, noch eine tägliche Sonnen- oder
Planetenparallaxe im Laufe einer Nacht (also quasi mit dem Erddurchmesser als Basislinie
unter Berücksichtigung der Planeteneigenbewegung) feststellen (s. Abb. 2.18). Da ihm
die daraus folgenden Entfernungen und Durchmesser der Sterne absurd erschienen, schuf
er ein Modell, bei dem die Erde im Mittelpunkt ruht und von der Sonne und dem Mond
58
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
M2 M1
M1
M2
Abb. 2.18.: Tägliche Parallaxe (links: rotierende Erde/feste Fixsternsphäre; rechts: feste Erde/rotierende Fixsternsphäre). Tycho konnte innerhalb einer Nacht nur die Eigenbewegung des Mars bezüglich der dahinter liegenden Fixsterne feststellen, die tägliche
Parallaxe war für ihn noch nicht messbar.
umkreist werden. Geometrisch gesehen der kopernikanischen Theorie gleichkommend
(mit Ausnahme der Entfernung zu den Fixsternen, weil eine ruhende Erde keine jährlichen
Parallaxen mit sich bringt), bewegen sich die anderen Planeten jedoch um Sonne. Auf die
Dimensionierung des Sonnensystems hat diese Sichtweise also keine Auswirkungen, nur
die Distanz zu den Sternen muss nicht mehr zwingend so groß sein.
Große Auswirkungen hatte die Arbeit Tychos auf den deutschen Astronomen Johannes
Kepler (1571 – 1630). Dieser verfügte im Gegensatz zu Tycho über die mathematischen
Fähigkeiten, dessen exakte Messdaten mit einem theoretischen Modell in Einklang zu
bringen. Dieses Modell sagte die Planetenbewegung besser voraus als alle vorhergehenden
und wird heute durch die drei keplerschen Gesetze zusammengefasst:
1. Die Planeten bewegen sich auf Ellipsen mit der Sonne in einem Brennpunkt.
2. Die Verbindungslinie zwischen Sonne und Planeten überstreicht in gleichen Zeiten
gleiche Flächen. D. h. der Planet bewegt sich umso schneller, je näher er der Sonne
kommt.
3. „... daß die Proportion, die zwischen den Umlaufzeiten irgendzweier Planeten besteht,
genau das Anderthalbe der Proportion der mittleren Abstände, d. h. der Bahnen selber,
ist, ...“ Dass Kepler damit nachfolgende Formel meint, wird durch ein angefügtes
Beispiel ersichtlich: „Wenn man also von der Umlaufzeit z. B. der Erde, die ein Jahr
beträgt, und von der Umlaufzeit des Saturn, die 30 Jahre beträgt, den dritten Teil der
Proportion, d. h. die Kubikwurzeln nimmt und von dieser Proportion das Doppelte
bildet, indem man jene Wurzeln ins Quadrat erhebt, so erhält man in den sich
59
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
ergebenden Zahlen die vollkommen richtige Proportion der mittleren Abstände der
Erde und des Saturn von der Sonne.“75 Also:
T1
T2
=(
a1
a2
3
)2
mit T1 und T2 als Umlaufzeit in Erdjahren und a1 und a2 als große Halbachsen der
Ellipsenbahnen.
Die ersten beiden Gesetze sind in Keplers Werk Neue Astronomie76 integriert, in dem er
die Modelle von Ptolemäus, Kopernikus und Tycho für die Marsbahn verglich und durch
eine elliptische Planetenbahn verbesserte, deren Exzentrizität jedoch nicht einmal 0,1
betrug (d. h., dass die Sonne um 10% der großen Halbachse vom Mittelpunkt verschoben
p
ist bzw. der minimale Abstand zum Mittelpunkt 1 − 0,12 ≈ 99,5% des maximalen, sprich
der großen Halbachse, beträgt)77 .
Erwähnenswert ist noch, dass das erste Gesetz alleine, also die Abkehr von der Epizykeltheorie, nicht die zentrale Errungenschaft Keplers war. Denn jede Ellipsenbahn kann auch
durch einen gegenläufigen Epizykel erzeugt werden, wie Abbildung 2.19 und die folgende
rechnerische Betrachtung78 verdeutlichen. Erst zusammen mit dem zweiten Gesetz, das
sich aus dem Äquantenmodell entwickelte und sich von diesem vom Ergebnis her nur
geringfügig unterscheidet, brach er die bis dahin alle Modelle bestimmende Regel der
gleichmäßigen kreisförmigen Bewegung.
Die Parameterdarstellung einer Ellipse mit großer Halbachse a und kleiner Halbachse b
lautet
x(t) = a cos(t)
y(t) = b sin(t),
die eines Epizykel mit Radius r und Deferentenradius R
x(t) = R cos(t) + r cos( f (t))
y(t) = R sin(t) + r sin( f (t)).
75
KEPLER, Johannes; CASPAR, Max (Hrsg.): Weltharmonik. Oldenburg, 1967, V: 3; S. 291f.
ASTRONOMIA NOVA
77
Nur Merkur besitzt mit ca. 0,2 eine größere Exzentrizität als Mars, was für den Minimalabstand zum
Mittelpunkt ca. 98% der Maximalentfernung bedeutet. Die anderen Planeten haben alle eine Exzentrizität,
die kleiner als 0,05 ist.
78
Vgl. DIXON, Laurence: On Epicycles and Ellipses.
wwwdata.unibg.it/dati/bacheca/63/21692.pdf – Zugriff am 1.10.2008.
76
60
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
D
d
Abb. 2.19.: Ellipsenbahn durch einen gegenläufigen Epizykel.
Mit cos(−t) = cos(t) und sin(−t) = − sin(−t) lässt sich die Ellipsendarstellung auf
x(t) =
y(t) =
a+b
2
cos(t) +
a+b
2
sin(t) +
a−b
2
a−b
2
cos(−t)
sin(−t)
erweitern. Vergleicht man diese Ausdrücke mit der Epizykeldarstellung, sieht man, dass jede
Ellipse ebenso als Deferent-Epizykel-Kombination mit R =
a+b
2
und r =
a−b
2
angeschrieben
werden kann, falls f (t) = −t. Umgekehrt ergibt sich a = R + r und b = R − r. Mit der
Sonne im Ursprung kann man die elliptische Erdbahn deshalb auch folgendermaßen mit
Epizykel angeben:
x E = x 0 + R cos(t) + r cos(t)
yE = R sin(t) − r sin(t)
mit x 0 =
p
a2 − b2 =
p
p
(R + r)2 − (R − r)2 = 2 Rr als Abstand der Sonne vom Mittel-
punkt der Ellipse bzw. der Exzentrizität.
Für eine geozentrische Betrachtung wie im ptolemäischen oder tychonischen Weltbild,
also mit der Erde im Ursprung, müsste man diese Koordinaten einfach zu x S = −x E bzw.
yS = −x E transformieren. Auch die Planetenbewegungen, bei denen die Exzentrizität
eine größere Rolle spielt, ließen sich so äquivalent zur heliozentrischen Ellipsentheorie
61
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
Abb. 2.20.: Keplers Modell vom Sonnensystem
darstellen, jedoch wären dazu vier Kreise aufeinander notwendig. Diese Hürde wurde von
Ptolemäus mit Hilfe von Annäherungen und Exzentrizitäten umgangen. Tycho fehlte dazu
wohl das mathematische Talent.
Das dritte Gesetz kommt in Keplers Weltharmonik79 vor, die die fünf Planetensphären
wie schon in seinem Weltgeheimnis80 in die fünf platonischen Körper (Tetraeder, Würfel,
Oktaeder, Dodekaeder, Ikosaeder) einbettet und mit einer Musiktheorie harmonieren
lässt (s. Abb. 2.20). Es scheint eher durch numerologisches Experimentieren mit den
ausgewerteten Messdaten von Tycho gefunden worden zu sein.
Berühmt wurde Kepler vor allem deswegen, weil seine drei Gesetze tatsächlich aus der
Mechanik Newtons, die erst Ende des 17. Jahrhunderts entstand, hervorgehen. Seine große
Leistung war neben seiner mathematischen Raffinesse und hohen Genauigkeit, dass er im
Gegensatz zu Kopernikus die wahre Sonne statt der mittleren ins Zentrum der Welt stellte.
Dies erleichterte die Bahnbeschreibungen der Planeten rechnerisch erheblich. Begründet
hatte er diesen Schritt damit, dass die Planetenbewegungen von einer von der Sonne
ausgehenden magnetartigen Kraft verursacht werden, die er die „Anima motrix“ nannte.
79
80
HARMONICES MUNDI
MYSTERIUM COSMOGRAPHICUM
62
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
Für die Entfernungen der Planeten bedeutete das dritte keplersche Gesetz eine Bestätigung einerseits der Angaben von Kopernikus, weil sie nun theoretisch gestützt wurden,
und andererseits der Messungen Tychos, weil die gut bekannten Umlaufzeiten fast die
gleichen Ergebnisse brachten. Keplers Ergebnisse sind in Tabelle 2.481 zusammengefasst
und in Abbildung 2.21 skizziert.
Tab. 2.4.: Keplers Ergebnisse für die mittleren Entfernungen der Planeten zur Sonne in AE (inkl. Maximal-/Minimalabstand, ± beschreibt also nicht den Fehler!), die zugehörigen
Umlaufzeiten in Jahren und die mittleren Abstände zur anderthalben Potenz.
Merkur
Venus
Erde
Mars
Jupiter
Saturn
0,388 ± 0,082
0,724 ± 0,005
1,000 ± 0,018
1,524 ± 0,142
5,200 ± 0,251
9,510 ± 0,542
0,241
0,615
1,000
1,881
11,862
29,457
0,242
0,616
1,000
1,881
11,858
29,327
Saturn
Jupiter
Mars
Abb. 2.21.: Die elliptischen Planetenbahnen nach Kepler (maßstabsgetreu ohne Rücksicht auf die
Perihelstellung und die Bahnneigung). Die Exzentrizität ist nur bei Merkur und Mars
gut erkennbar.
Im Buch Neue Astronomie befasste sich Kepler auch mit der fehlenden horizontalen
Parallaxe des Mars in Opposition, wo der Planet der Erde am nächsten steht. Daraus schloss
81
Vgl. KEPLER: Weltharmonik, V: 4; S. 297f & 295.
63
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
er, dass diese höchstens der Messgenauigkeit Tychos entsprechen kann, also etwa „20 bis
0
2 12 “82 . Der Sonne, die sich fast doppelt so weit weg befindet, ordnete er folglich eine
kleinere Parallaxe zu.
Zunächst wählte er eine Entfernung von 1 800 Erdradien, die einer Parallaxe von 1,90 entspricht, weil dies dem 30-fachen Mondabstand gleichkam und somit ein numerologischer
Zusammenhang zur Anzahl der Tage eines Monats bestand83 . Dieser Wert passte außerdem
gut zu seinen früher angestellten Überlegungen mit Hilfe des Eklipsendiagramms84 .
Aristarchs Methode der Dichotomie verwarf er als zu ungenau, nachdem er ein Verhältnis
◦
zwischen Sonnen- und Monddistanz von 23 : 1 errechnete85 (entspricht 2 12 zwischen
Halbmond und Quadratur bzw. 1 380 Erdradien Sonnenabstand bei einem Mondabstand
von 60 Erdradien bzw. fast 2,50 horizontaler Parallaxe).
In einem späteren Werk kommt er durch nachfolgende numerologische Überlegungen
auf eine Entfernung von fast 3500 Erdradien, also immerhin das Dreifache des bisher
anerkannten Wertes für die Astronomische Einheit. Die erfundene Annahme, dass sich die
Volumen von Sonne und Erde gleich zueinander verhalten wie der Sonnenabstand zum
Erdradius, also
rS3 : rE3 = dS : rE ,
führt in Einheiten des Erdradius zu rS3 = dS und mit 300 für den Winkeldurchmesser der
Sonne, also dS =
rS
tan 150
≈ 229rS , zu
rS ≈ 15 Erdradien,
dS ≈ 3 469 Erdradien.
Dieses Ergebnis86 entspricht ziemlich genau dem „harmonischen“ Wert von etwa 10 für die
horizontale Parallaxe und wurde zusätzlich durch eine ähnliche Relation bezüglich des
Mondes von Kepler bestärkt, die den gewohnten Wert für Mondentfernung ergibt:
Mit
rE3 : rM3 = dM : rE ,
82
KEPLER, Johannes; CASPAR, Max (Hrsg.): Neue Astronomie. Oldenburg, 1929, 64; S. 370.
KEPLER, Johannes; FRISCH, Christian (Hrsg.): Joannis Kepleri astronomi opera omnia 7. Band 7, Heyder &
Zimmer, 1868, S. 483.
84
Vgl. KEPLER, Johannes; CASPAR, Max (Hrsg.): Gesammelte Werke: Astronomia nova. Band 3, Beck, 1937,
S. 129.
85
KEPLER: opera 7, S. 486.
86
Vgl. KEPLER, Johannes; CASPAR, Max (Hrsg.): Gesammelte Werke: Epitome Astronomiae Copernicanae.
Band 7, Beck, 1953, IV: 1; S. 277ff.
83
64
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
in Einheiten des Erdradius also rM3 =
1
dM
und aufgrund desselben Winkeldurchmessers des
Mondes (d. h. dM ≈ 229rM ) erhält man
rM ≈ 0,257 Erdradien,
dM ≈ 58,9 Erdradien.
Außerdem ergeben sich durch Umformulierung die „harmonischen“ Zusammenhänge
rE : dM = dM : dS = rM : rS = 1 : 58,9,
die die Mondentfernung zur zentralen Proportion machen.
Für die Entfernung der Fixsterne stellte Kepler analoge Überlegungen an. Seiner harmonischen Theorie nach galt die Beziehung
rSonne : dSaturn – Sonne = dSaturn – Sonne : dFixsterne – Sonne ,
was mit oben genannten Ergebnissen (dSaturn – Sonne = 9,51 · 229rS ≈ 2 000rS ) zu einer Distanz
von etwa 4 000 000 Sonnenradien bzw. 60 000 000 Erdradien bzw. über 17 000 seiner AE
zu den Fixsternen führt. Diese Entfernung passt wiederum zu Tychos Messdaten, denen
zufolge die jährliche Sternparallaxe weniger als 10 betragen muss87 .
2.3.3. Die Erfindung des Teleskops
Eine neue Ära der Astronomie wurde größtenteils von Galileo Galilei (1564 – 1642) aufgrund seiner Himmelsbeobachtungen mit einem Teleskop88 , das wahrscheinlich 1608 vom
niederländischen Brillenmacher Hans Lippershey erfunden wurde, eingeleitet. Seine Beobachtungen der Sonnenflecken und deren Bewegung über die Sonnenscheibe sowie der
zerklüfteten Oberflächenstruktur des Mondes ließen, wie auch schon Tychos Kometen- und
Supernovabeobachtung, Zweifel an den ptolemäisch-aristotelischen Thesen von perfekten
ewigen Himmelskörpern aufkommen. Starke Argumente zugunsten des heliozentrischen
Weltbildes lieferte die Entdeckung der Jupitermonde, wodurch die Erde nicht mehr der
einzige Mittelpunkt von Bewegungen war, und der Phasen der Venus, die das ptolemäische
Weltbild nicht erklären konnte. Außerdem wurden die Planeten im Gegensatz zu den
Sternen nicht mehr nur als Punkte gesehen, was darauf hinwies, dass es sich um mondbzw. erdähnliche Körper handle.
87
88
Vgl. KEPLER: Epitome, IV: 1; S. 285ff.
gr. τηλε- (tele-) „fern“, σκoπεω (skopeo) „sehen“
65
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
Bessere und immer größere Teleskope und Erfindungen wie die Mikrometerschraube
verhalfen im Laufe des angebrochenen Jahrhunderts zu einem Konsens bezüglich der
scheinbaren Größen der Planeten, die bisher viel zu groß angenommen und nun beispielsweise bei den von Kepler vorausgesagten Merkur- und Venuskonjunktionen von 1631 und
1639, bei denen die Planeten direkt vor der Sonne als Schatten gesehen werden konnten,
gemessen wurden.
Entscheidende Fortschritte für den Wert der Astronomischen Einheit erzielte um 1650 der
belgische Astronom Gottfrid Wendelin (1580 – 1667). Unter der haltlosen Annahme, dass
alle Planeten von der Sonne aus gesehen annähernd unter demselben Winkeldurchmesser
von etwa 2900 erscheinen, die Planetendurchmesser also proportional zu ihrer Entfernung
zur Sonne sind89 , hat die Sonne folglich eine horizontale Parallaxe von höchstens 1500 .
Dieses Ergebnis bestätigte er durch Aristarchs Dichotomiemethode, bei der er für den
◦
Winkel zwischen Halbmond und Sonne 89 34 maß. Für die Sonnenentfernung bedeuten
diese Werte die 229-fache Mondentfernung bzw. etwa 14 000 Erdradien, also schon mehr
als die Hälfte der tatsächlichen Distanz.90
Etwa zur selben Zeit stellte Giovanni Domenico Cassini die Hypothese auf, dass die
horizontale Parallaxe der Sonne aufgrund von Abweichungen von einer theoretischen
Sonnenposition höchstens 1200 betragen kann. Darauf kam er, indem er mit einem sehr
großen Gnomon (eigentlich ein Loch in der Mauer der Kathedrale von Bologna) den Stand
der Sonne bei den Sonnwenden genauestens maß und durch Halbierung der Summe
dieser Deklinationen die Schräge der Erdachse zur Ekliptik berechnete. Dabei fiel ihm auf,
dass zwischen dem so bestimmten Himmelsäquator und dem durch Zirkumpolarsterne
bestimmten Himmelspol nicht genau 90◦ liegen. Die Abweichung von über 20 erklärte er
teils durch Refraktion91 , wobei er als erster das Brechungsgesetz von Snellius verwendete,
teils durch die geozentrische Parallaxe der Sonne (s. Abb. 2.22).92
Genauer bestimmen wollte Cassini, mittlerweile an die französische Akademie der Wissenschaften berufen, die Astronomische Einheit durch Bestimmung der Parallaxe des Mars
einerseits durch Vergleich einer beobachteten Position mit der mit Hilfe von Ephemeriden93
89
Diese Theorie trifft in Wahrheit nur auf Merkur, Erde und Saturn zu, aber mit einem Winkeldurchmesser
von ca. 17,400 .
90
Vgl. HELDEN, Albert Van: Measuring the Universe – Cosmic Dimensions from Aristarchus to Halley.
broschierte Auflage. Univ. of Chicago Press, 1986, S. 112f.
91
Richtungsänderung eines auf die Erde treffenden Lichtstrahls aufgrund von Brechung wegen der nach
unten zunehmenden Dichte in der Atmosphäre. Dieses Phänomen war schon Ptolemäus bekannt, wurde
◦
aber erstmals von Tycho bei seinen Messungen berücksichtigt. Die Abweichungen betragen ca. 12 am
Horizont und 10 bei einer Höhe von 45◦ .
92
Vgl. ibid., S. 129ff.
93
Positionstabellen von Himmelskörpern
66
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
SS
SS
Atmosphäre
l1
Äquator
l2
m1
f1
f2
Äquator
m2
Erde
Erde
WS
WS
Abb. 2.22.: Sonnenparallaxe nach Cassini. Die Abweichung der Sonnenstände bei den Sonnwenden
(SS =Sommersonne, W S =Wintersonne) erklärte Cassini durch Refraktion (links: λ1
und λ2 ) und die endliche Entfernung der Sonne, also durch die Parallaxe (rechts: µ1
und µ2 )
berechneten (wie schon Tycho und Kepler), andererseits durch gleichzeitige Beobachtung
von verschiedenen Orten aus. Da Mars 1672 mit etwa 0,38 AE (vgl. Keplers Daten für die
Marsbahn in Tab. 2.4) in seiner seltenen erdnächsten Position (Mars in Opposition und im
Perihel) und somit die Parallaxe mehr als 2 12 mal größer als die der Sonne sein würde, startete eine Expedition unter der Führung von Jean Richer nach Cayenne (Französisch-Guyana;
vgl. Abschn. 1.3), um dort dieselben Beobachtungen zur selben Zeit94 durchzuführen wie
Cassini in Frankreich. Außerdem waren in Äquatornähe die Abweichungen der Sonnenposition durch Refraktion aufgrund des geringen Abstandes vom Zenit viel kleiner. Aus dem
Vergleich der Messdaten aus Cayenne von Mars und Sonne und der Messung der täglichen
Parallaxe in Frankreich kam Cassini teils durch etwas dubiose Mittelungen weit gestreuter
Werte, teils durch behutsam ausgewählte Daten auf eine horizontale Marsparallaxe von
00
ca. 2500 , also eine Sonnenparallaxe von 9 12 , die wiederum fast 22 000 Erdradien für die
Astronomische Einheit entspricht.95
Sein Resultat wurde wahrscheinlich durch das Ergebnis der Messungen des Engländers
John Flamsteed (1646 – 1719) beeinflusst, der die günstige Marsposition ebenfalls zur
Bestimmung der täglichen Marsparallaxe ausnutzte. Im Gegensatz zu Cassini und Richer,
die mit Hilfe von Pendeluhren die Bewegungsdauer der Planeten im Bezug auf den Fixsternhintergrund maßen, verwendete er eine Mikrometerschraube für die Justierung seines
94
Zur Synchronisierung der Uhren wurden Eklipsen der Jupitermonde und Abstandmessungen des
Erdmondes zu ausgewählten Fixsternen verwendet.
95
Vgl. HELDEN: Measuring the Universe, S. 137ff.
67
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
Teleskops und kam schon früher zur Auffassung, dass die Parallaxe des Mars nicht größer
als 2500 sei, die der Sonne folglich höchstens 1000 .96
Aufgrund der großen Streuung dieser und weiterer Messungen konnte bis in die zweite
Hälfte des 17. Jahrhunderts kein Konsens für die Sonnenparallaxe erreicht werden. Relativ
einig war man sich nur, dass sie weniger als 2000 betrage, bestärkt durch eine theoretische
Überlegung Newtons um 1670. Er behauptete, dass die Zentripetalbeschleunigung, die
den Mond um die Erde kreisen lässt, größer sein müsse als jene, die die jährliche Rotation
des Erde-Mond-Ensembles bewirkt, weil der Mond sonst der Sonne immer dieselbe Seite
zuwenden würde und nicht der Erde. Da die Zentripetalbeschleunigung im Abstand d vom
Zentrum allgemein dω2 ist und ω =
2π
T
dM νM > dS νS
2
2
= 2πν, gilt
⇒
dS <
dM νM2
νS2
.
Mit dM = 60rE , νS = 1a−1 und νM = 13,369a−1 ergibt das dS < 10 723rE , einer Sonnenparallaxe von ca. 19,200 entsprechend.97
2.3.4. Venustransite
Die Venus kommt der Erde in Konjunktion mit der Sonne mit weniger als 0,3 AE noch
näher als der Mars und hat dort somit fast die vierfache Parallaxe der Sonne, jedoch ist sie
dann wegen ihrer Sonnennähe außer bei direkten Durchgängen nicht beobachtbar. Diese so
genannten Transite98 kommen wegen der Neigung des Venusorbits zur Ekliptik höchstens
zweimal pro Jahrhundert, zumindest aber alle 120 Jahre vor, dann aber meist im Abstand
von 8 Jahren. Nachdem die ersten Beobachtungen solcher astronomischen Erscheinungen
1631 und 1639 wie schon erwähnt nur zur Bestimmung des scheinbaren Durchmessers der
inneren Planeten verwendet wurden, hatte der schottische Mathematiker und Astronom
James Gregory (1638 – 1675) die Idee, dass man mit Beobachtungen eines Durchgangs von
zwei möglichst weit entfernten Punkten auf der Erde die Entfernung zur Sonne berechnen
könne99 (s. Abb. 2.23).
Der u. a. für die richtige Vorhersage der Wiederkehr eines (heute nach ihm benannten)
Kometen berühmte Edmond Halley (1656 – 1742) wurde zum größten Befürworter dieser
96
Vgl. HELDEN: Measuring the Universe, S. 134ff.
Vgl. HALL, A. Rupert: Newton on the calculation of central forces. Annals of Science, 13 1957, S. 67f.
98
lat. transire „vorübergehen“
99
Vgl. GREGORY, James: Optica Promota. excudebat J. Hayes, pro S. Thomson, ad insigne Episcopi, 1663,
Prop. 87.
97
68
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
Sonne
Ä
Venus
2
1
P
N
E
3
4
Erde
(a) Venustransit vom Erdmittelpunkt und vom Nordpol aus gesehen
(b) Spur des Venusmittelpunktes auf
der Sonnenscheibe
Abb. 2.23.: (a): Vom Nordpol erscheint der Transit wegen der geografischen Breite tiefer (übertrieben dargestellt). Aus diesem Höhenunterschied ließe sich die Parallaxe der Venus
und der Sonne bestimmen, jedoch beträgt dieser in Wahrheit nur etwa ein 60stel der
Sonnenscheibe und ist deshalb ähnlich schwer direkt messbar wie die Parallaxe des
Mars.
(b): Die Spur ist eine Zentralprojektion (durch den sich bewegenden Mittelpunkt der
Venus) desjenigen Weges auf die Sonnenoberfläche, den ein Beobachter im Raum zurücklegt. Somit wird die Spur von der Bewegung des Venus- und des Erdmittelpunktes
um die Sonne, sowie der tägliche Rotation der Erde beeinflusst. Die Spuren vom Erdmittelpunkt (E) und vom Nordpol (N) aus gesehen verlaufen annähernd parallel. Für
andere Standorte, beispielsweise am Äquator oder einer anderen nördlichen Breite,
ändert sich während dem Transit wegen der täglichen Erdrotation der Abstand zur Ekliptik und deshalb sind die von dort gesehenen Spuren (Ä bzw. P) ein wenig gekrümmt
und sogar leicht unterschiedlich geneigt (übertrieben dargestellt). Die am leichtesten
messbare Diskrepanz stellt die unterschiedliche beobachtete Dauer des Transits dar, weil
die Zeiten vom ersten Kontakt des Venusabbildes mit der Sonnenscheibe (1; externer
Kontakt beim Ingress) bis zum Austritt (4; vierter Kontakt oder externer Kontakt beim
Egress) bis zu mehreren Minuten voneinander abweichen. Exakter zu beobachten sind
der zweite und dritte Kontakt (2 & 3; interner Kontakt beim Ingress bzw. Egress).
69
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
Vorgehensweise. Denn nachdem er 1677 als erster einen Merkurtransit von Anfang bis
Ende beobachten konnte und ihn die genaue Messbarkeit der Zeitpunkte des so genannten
zweiten und dritten Kontakts (interner Kontakt beim Ingress bzw. Egress; s. Abb. 2.23 (b))
beeindruckte, war er davon überzeugt, dass damit die Astronomische Einheit im Gegensatz
zu bisherigen Methoden mit noch nie erreichter Genauigkeit bestimmt werden könnte.
Obwohl er selbst die nächsten Venustransite, die im Juni 1761 und 1769 auftraten, nicht
mehr erleben würde, forcierte er insbesondere mit seiner bekannten Abhandlung über
eine einzigartige Methode, wie man die Sonnenparallaxe oder den Abstand zur Erde mit Hilfe
einer Beobachtung der Venus in der Sonne bestimmen können wird100 , die Bestrebungen für
weltweite Expeditionen. In diesem Aufruf an Astronomen der folgenden Generation weist
00
er mit einer angenommen Sonnenparallaxe von 12 12 auch auf die günstigen Beobachtungsorte Port Nelson an der Hudson Bay und die Gangesmündung in Ostindien hin und
gibt konstruierte Ergebnisse an. Gegen Ende schreibt er:
„Deshalb empfehle ich aufs eifrigste wieder und wieder den Wißbegierigen,
sich dieser Beobachtung zu widmen.
Hierdurch kann die Sonnenparallaxe bis auf ihren 500. Teil gefunden werden,
was zweifellos manchen überraschend erscheinen wird. Dennoch, wenn eine
genaue Beobachtung an beiden oben erwähnten Orten zu haben sein wird, ist
es bereits gezeigt worden, daß die Dauer des Venusdurchganges um 17 volle
Minuten vo[n]einander abweichen, unter der Annahme, daß die Parallaxe der
00
Sonne 12 12 beträgt. Und wenn durch die Beobachtung entdeckt wird, daß
diese Abweichung größer oder kleiner ist, so wird die Parallaxe der Sonne
beinahe im gleichen Verhältnis größer oder kleiner sein.“101
Wie Halley auf die Zeitdifferenz von 17 Minuten kam, wird von L. W. B. Browne eingehend
diskutiert102 . Entscheidend für die Genauigkeit dieser Methode ist, dass die Parallaxe
der Sonne statt aus sehr kleinen Winkelunterschieden aus relativ großen Zeitdifferenzen
hergeleitet werden kann, wenn auch die von Halley genannten 0,2 % Messunsicherheit
nicht erreicht werden konnten.
Tatsächlich waren in den Jahren 1761 und 1769 zahlreiche britische, französische und
sogar ein österreichischer Beobachter, nämlich der Jesuit Maximilian Hell (1720 – 1792), an
100
HALLEY, Edmond: Methodus singularis qua Solis parallaxis sive distantia a Terra, ope Veneris intra Solem
conspiciendoe, tuto determinari poterit. Philosophical Transactions of the Royal Society, 29 1714 – 1716.
101
Aus ZINNER, Ernst: Astronomie – Geschichte ihrer Probleme. Band Orbis Academicus, II/1, Alber, 1951,
S. 239.
102
BROWNE, L.W. B.: Halley’s Method for Calculating the Earth – Sun Distance. Archive for History of Exact
Sciences, 59 2005.
70
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
den abgelegensten Orten der Erde: Südafrika, Norwegen, Kalifornien, Neufundland, Indien,
Sibirien und die wohl berühmteste Messung unter der Leitung von Captain James Cook auf
Tahiti im Südpazifik. Bemerkenswert sind diese Unternehmungen, weil sie zu den ersten
international aufeinander abgestimmten wissenschaftlichen Zusammenarbeiten zählen, die
insbesondere wegen des Siebenjährigen Kriegs (1756 – 1763) keineswegs selbstverständlich
war.
James Short (1710 – 1768) veröffentlichte im Dezember 1762 seine Ergebnisse103 , die
er aus einer Sammlung von 15 gemessenen Datensätzen, insbesondere aus dem Vergleich
zwischen Greenwich und dem Kap der Guten Hoffnung, durch eine ähnliche Vorgehensweise wie Halley erlangte. Den eigentlichen Wert der Sonnenparallaxe berechnet er sogar
exakt nach der Empfehlung Halleys: Ausgehend von einem hypothetischen horizontalen
00
Parallaxe der Sonne von 8 12 am Tag des Transits berechnete er, dass ein Beobachter am
Kap den dritten Kontakt 6 Minuten und 8 Sekunden später als ein theoretischer Beobachter
im Erdmittelpunkt sähe, während der Austritt der Venus in Greenwich schon 1 Minute und
11 Sekunden früher begänne. Da die resultierende Zeitdifferenz von 7 Minuten und 19
Sekunden aber um 4 Sekunden länger ist als die gemessene, ist auch die angenommene
Sonnenparallaxe im selben Verhältnis größer als die tatsächliche: also
7 min 19 s
7 min 15 s
=
439 s
435 s
=
8, 500
α
.
Auf dieselbe Weise verglich Short die Beobachtungen der 14 anderen Orte mit denen am
Kap der Guten Hoffnung und kam so auf einen Mittelwert von 8,4700 für α bzw. 8, 5200 ,
wenn er die vier am meisten abweichenden Messdaten missachtete. Daraus berechnete er
mit dem aus den keplerschen Gesetzen gewonnenen Abstand der Erde zur Sonne am Tag
des Transits (1,015 AE) die durchschnittliche horizontale Sonnenparallaxe:
rE = 1,015 AE sin 8, 5200 = 1 AE sin ᾱ
⇒
ᾱ = 8, 6500
Dies entspricht einer Astronomischen Einheit von ca. 23 846 Erdradien und liegt sehr nahe
am tatsächlichen mittleren Wert von 8,79400 bzw. 23 455 Erdradien. Der Fehler von über
1,6 % erfüllte jedoch nicht Halleys Erwartungen.
103
Vgl. SHORT, James: The Observations of the Internal Contact of Venus with the Sun’s Limb, in the Late
Transit, Made in Different Places of Europe, Compared with the Time of the Same Contact Observed at the
Cape of Good Hope, and the Parallax of the Sun from Thence Determined. Philosophical Transactions of
the Royal Society, 52 1761 – 1762.
71
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
00
Auf die Frage, wie Short auf seine Zeitdifferenzen und die 8 12 kam, wird nun näher
eingegangen, jedoch mit zeitgemäßen mathematischen Mitteln104 .
Zunächst werden zwei kartesische Koordinatensysteme eingeführt: ein geozentrisches
äquatoriales x 0 y 0 z 0 (d. h. mit dem Erdmittelpunkt im Ursprung, die z 0 -Achse durch den
Nordpol und dem Äquator folglich in der x 0 y 0 -Ebene) und ein heliozentrisches ekliptikales
x yz (d. h. mit dem Sonnenmittelpunkt im Ursprung und die Erdumlaufbahn in der x yEbene). Die positive x 0 -Achse soll so orientiert sein, dass sie am Tag des Frühlingsbeginns
genau durch den Sonnenmittelpunkt verläuft. Diese Richtung behalte sie bei, unabhängig
von der täglichen und jährlichen Bewegung der Erde, mit anderen Worten verändert
der Ursprung seine Position, während die Achsenrichtungen im Raum fix bleiben. Die
positive x-Achse zeige genau zur Halbzeit des Transits vom Erdmittelpunkt aus gesehen
auf selbigen.
Die Koordinaten eines Beobachters auf der Erde lassen sich mit Hilfe der geographische
Länge λ und Breite ϕ unter der üblichen Konvention angeben, also −180◦ < λ ≤ 180◦
und −90◦ ≤ ϕ ≤ 90◦ , wobei λ > 0 östlich von Greenwich und ϕ > 0 nördlich des
Äquators bedeutet. Die Umrechnung in das kartesische Koordinatensystem x 0 y 0 z 0 erfolgt
folgendermaßen:
  

x0
rE cos ϕ cos(θ + λ)
  

 y 0  =  r cos ϕ sin(θ + λ)  ,
   E

0
z
rE sin ϕ
wobei θ für den sich kontinuierlich ändernden Winkelabstand des Nullmeridians von der
x 0 -Achse durch die tägliche Erdrotation und rE für den Erdradius steht, jedoch in Einheiten
des Erdabstands zur Sonne, also rE ≈
ein).
8,500
dS
(hier fließt die angenommene Sonnenparallaxe
Um nun vom geozentrischen ins heliozentrische Koordinatensystem zu transformieren (s.
Abb. 2.24), muss man zuerst um den Winkel " (die Neigung der Erdachse gegenüber der
Ekliptik) um die x 0 -Achse drehen, sodass die x 0 y 0 -Ebene mit der x y-Ebene übereinstimmt.
Als nächstes bewirkt eine Drehung um die z 0 -Achse (die schon in dieselbe Richtung wie
die z-Achse zeigt) um den Winkel ψ, dass die x 0 -Achse mit der x-Achse zusammenfällt. ψ
beschreibt also die Erdposition im Bezug auf die Sonne am Tag des Transits, ist demnach
gleich dem Winkelabstand vom Herbstpunkt (weil dort die x 0 - und die x-Achse gleich
orientiert wären) bzw. vom Frühlingspunkt plus 180◦ . Abschließend wird das Koordinatensystem x 0 y 0 z 0 um eine Längeneinheit in die positive x-Richtung verschoben. Auf diese
104
Nach TEETS, Donald A.: Transits of Venus and the Astronomical Unit. Mathematics Magazine of the
Mathematical Association of America, 76 2003, Nr. 5.
72
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
z’
Frühlingsbeginn
z’
z
x’
e
y’
t=0
e
y
x
Sonnenmittelpunkt
y’
x’
y
Abb. 2.24.: Koordinatentransformation vom geozentrischen äquatorialen ins heliozentrische ekliptikale System.
Einheit werden sich die späteren Ergebnisse beziehen. Sie stellt jedoch nicht genau 1 AE
dar, weil sich die Erde ja nicht in ihrer mittleren Entfernung zur Sonne befindet. Formal
lautet die Transformation

   
  
1
0
0
x0
1
x
cos ψ sin ψ 0
  

   
 y  = − sin ψ cos ψ 0 0 cos " sin "   y 0  + 0 .

   
  
z0
0
z
0
0
1
0 − sin " cos "
In den Moment der Halbzeit des Transits vom Erdmittelpunkt aus gesehen wird der
Zeitpunkt t = 0 gelegt. Die Position des Nullmeridians im Bezug auf die x 0 -Achse zu diesem
Zeitpunkt wird θ0 genannt. Für Zeiten nach t = 0 muss θ wegen der täglichen Rotation
der Erde um ihre Achse nach Osten vergrößert werden, und zwar um etwas mehr als 15◦
pro Stunde (weil sich die Erde in 24 Stunden wegen des Unterschieds zwischen einem
Sterntag und einem Sonnentag um fast 361◦ um die eigene Achse dreht). Analog muss θ
verkleinert werden, um Zeitpunkte vor t = 0 betrachten zu können. Deshalb wird θ durch
θ0 ± 15,041◦ /h · t ersetzt.
Die jährliche Bewegung kann für die kurze Dauer eines Venustransits ausreichend gut
durch eine lineare Bewegung in positiver y-Richtung angenähert werden. Mit der Winkel-
73
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
z
rS
x
y
rV
d
z
^
R
t=0
t=T
Abb. 2.25.: Spur des Venusabbildes auf der Sonnenscheibe.
>
geschwindigkeit ωE der Erde im Bezug auf die Sonne erhält man den Vektor 0 ωE t 0 ,
>
der mit obigem x y z
addiert wird. Somit erhält man die x yz-Koordinaten eines
Beobachters mit geographischer Länge λ und Breite ϕ zur Zeit t.
Der Kern dieser Rechenmethode liegt nun darin, Vektorgleichungen aufzustellen, die auf
der Tatsache basieren, dass der Erdmittelpunkt, der Venusmittelpunkt und der Mittelpunkt
des Abbildes der Venus auf der Sonne kollinear sind. Danach werden dieselben Gleichungen
für Beobachter auf der Erdoberfläche ausgeführt.
Abbildung 2.25 zeigt den Weg des Venusabbildes auf der Sonnenscheibe vom Erdmittelpunkt aus gesehen. Zur Zeit t = 0 befindet sich der Mittelpunkt des Venusabbildes
>
in x yz-Koordinaten im Punkt ~I0 = 0 d cos ξ d sin ξ , der Erdmittelpunkt im Punkt
>
~ = 1 0 0
~ = ~I + v( E
~ − ~I ), wobei v
E
und das Zentrum der Venus im Punkt V
0
0
0
0
0
den Abstand der Venus von der Sonne darstellt. Zur Zeit t = T des dritten Kontakts
vom Erdmittelpunkt aus gesehen befindet sich das Zentrum des Venusabbildes im Punkt
>
~I = 0 R̂ cos(ξ + ζ) R̂ sin(ξ + ζ) , wobei R̂ = r − r . In derselben Zeit hat sich der
T
S
V
>
~ = 1 ω T 0
Erdmittelpunkt nach E
bewegt. Die Bewegung der Venus wird ebenfalls
T
E
linear in einer zur yz-Ebene im Abstand v parallelen Ebene angenähert, aber im Bezug auf
die Ekliptik ist die Venusbahn um den Winkel ι geneigt. Mit ωV für die Winkelgeschwin-
74
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
z
x
i
t=0
t=T
y
Abb. 2.26.: Bewegung der Venus in der Ebene x = v.
digkeit der Venus kann die Position des Planeten zur Zeit T folgendermaßen approximiert
werden (s. Abb. 2.26):

0



~ =V
~ + vω T  cos ι  .
V
T
0
V


− sin ι
~ − ~I wegen der Kollinearität der Punkte ein
Wie schon angedeutet, muss der Vektor V
T
T
~ − ~I sein. Wegen der ersten Koordinate muss die entsprechende
Vielfaches des Vektors E
T
T
~ −~I = v( E
~ −~I )
Konstante gleich v sein. Aus der zweiten Koordinate der Vektorgleichung V
T
T
T
T
gewinnt man durch Auflösen von cos(ξ + ζ), Ersetzen von cos ζ durch
p
R̂2 −d 2
, sowie Kürzen
R̂
v(ωE − ωV cos ι)
T.
sin ξ =
p
(1 − v) R̂2 − d 2
d
R̂
und sin ζ durch
Analog erhält man aus der dritten Koordinate durch Erweitern von sin(ξ + ζ) und Vereinfachen
cos ξ = −
vωV sin ι
T.
p
(1 − v) R̂2 − d 2
Mit der Identität sin2 ξ + cos2 ξ = 1 erhält man
T=
1−v
v
s
R̂2 − d 2
ω2V + ω2E − 2ωV ωE cos ι
75
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
für die halbe Dauer eines Venustransits vom Erdmittelpunkt aus gesehen und kann damit
auch den Wert von sin ξ und cos ξ angeben.
Nun wird die Rechnung für einen Beobachter auf der Erdoberfläche wiederholt. Der
Zeitpunkt des dritten Kontakts für diesen sei t = T̃ , wobei sich t = 0 immer noch auf
die Halbzeit des Transits für einen Beobachter im Erdmittelpunkt bezieht. Weiters stehe
>
~I = 0 y z
für den Ort der Zentrums des Venusabbildes auf der Sonne zur Zeit
T̃
T̃
T̃
t = T̃ . Die Position des Beobachters zur Zeit t = T̃ ist mit obigen Ausführungen
  

x
0
  

~ =  y  + ω T̃  .
O
T̃
   E 
z
0
~ erlangt man
Durch Ersetzen von T durch T̃ bei V
T

0



~ =V
~ + vω T̃  cos ι  .
V
0
V
T̃


− sin ι
~ − ~I sein und mit der
~ − ~I ein Vielfaches des Vektors O
Wie vorher muss der Vektor V
T̃
T̃
T̃
T̃
v
~
~ − ~I ).
ersten Koordinate berechnet man die Konstante und erhält somit V − ~I = v ( E
x
T̃
T̃
x
T̃
T̃
Mit den übrigen Koordinaten gewinnt man yT̃ = M + N T̃ , wobei
M=
(1 − v)x d cos ξ − v y
x−v
und
N=
x vωV cos ι − vωE
ist,
x−v
und zT̃ = P + Q T̃ , wobei
P=
(1 − v)x d sin ξ − v y
x−v
und
Q=
x vωV sin ι
x−v
ist.
Mit y 2 + z 2 = R̂2 berechnet man T̃ , wobei die positive Wurzel den richtigen Wert ergibt.
T̃
T̃
Ein Beobachter mit geographischer Länge λ und Breite ϕ bzw. den entsprechenden
x yz-Koordinaten sollte den dritten Kontakt demzufolge um T̃ − T Stunden später als der
konstruierte Beobachter im Erdmittelpunkt sehen, falls die Differenz positiv ist, und um
T̃ − T Stunden früher, falls die Differenz negativ ist.
76
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
Folgende Werte für die verschiedenen Parameter müssen Short bekannt gewesen sein
und können großteils in seiner Veröffentlichung105 (zumindest indirekt) gefunden werden:
• v ≈ 0,715 Längeneinheiten (LE), wobei 1 LE wie gesagt die Entfernung Erde–Sonne
am Tag des Transits darstellt.
Diesen Wert konnte er mit Hilfe der keplerschen Gesetze berechnen, die der Venus
zum gesuchten Zeitpunkt eine Entfernung von 0,726 AE, der Erde 1,015 AE vorhersagen. Es gilt: 0,726 AE : 1,015 AE = 0,715 LE : 1 LE. Bei Short ist nur erwähnt, dass die
Differenz zwischen Venus- und Sonnenparallaxe am Tag des Transits 21,3500 beträgt.
Davon lässt sich der genannte Betrag ableiten, indem man mit der Venusparallaxe
r
00
E
(21,3500 + 8,500 ) den Abstand der Venus von der Erde ( sin 29,85
00 mit rE = 1 LE sin 8,5 )
berechnet und diesen von 1 abzieht.
• ωE ≈ 20 23,500 /h
Laut drittem keplerschen Gesetz (Flächensatz) gilt in guter Näherung v̄r̄ = vr.
Schreibt man ωr statt v, kommt man auf ω =
r̄ 2
ω̄,
r2
wobei ω̄ =
360◦
,
365,2425·24 h
weil
ein Jahr im gregorianischen Kalender durchschnittlich 365,2425 Tage dauert. Teets
verwendet hier den Wert 20 2500 /h 106 .
• ωV = 30 59,800 /h
Diesen Wert findet man bei Short und berechnet man analog zum ωE aus der Umlaufzeit der Venus (mit aktuellen Werten: 30 58,300 /h ).
• ι ≈ 3,4266◦
Bei Short sind für den Winkel zwischen Venusorbit und Ekliptik 8◦ 3000 100 angegeben,
jedoch vermute ich, dass er damit den Winkel zwischen Venusspur und Ekliptik vom
Erdmittelpunkt aus gesehen meinte. Dieser erscheint wegen der jährlichen Bewegung
der Erde größer als die tatsächliche Neigung ι der Venusbahn. Shorts Wert steht
über folgende Gleichung mit ι in Verbindung: arctan ω
ωV sin ι
V
cos ι−ωE
= 8◦ 300 1000 . Hierbei
wurde einfach die Winkelgeschwindigkeit der Venus ωV in ihre Komponenten zerlegt
und vom horizontalen Anteil ωV cos ι (d. h. parallel zur x y-Ebene) die momentane
Winkelgeschwindigkeit der Erde ωE abgezogen und anschließend der resultierende
Winkel berechnet, den eben gerade die scheinbare von Short gegebene Neigung der
Venusbahn angibt. Teets geht hier von einem Druckfehler aus und verwendet den
Wert 3◦ 3000 100107 .
SHORT: Philosophical Transactions of the Royal Society 52 [1761 – 1762], S. 625.
Vgl. TEETS: Mathematics Magazine of the Mathematical Association of America 76 [2003], S. 345.
107
Vgl. ibid.
105
106
77
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
• R̂ ≈ 0,004441 LE
Dies entspricht 150 1600 bzw. der halben Differenz der von Short angegebenen Winkeldurchmesser der zwei Gestirne (Sonne: 310 3100 , Venus: 5900 ).
• d ≈ 0,002773 LE
Diesen Wert findet man entsprechend bei Short (90 3200 ).
• ψ ≈ 255,5◦
Diesen Betrag erhält man anhand der Überlegung, dass die Erde die 90◦ des Orbits
zwischen Frühlings- und Sommerbeginn in 93 Tagen zurücklegt. Da der Transit
am 6.Juni, also 15 Tage vor Sommerbeginn stattfand, fehlten der Erde zu diesem
Zeitpunkt etwa
15
90◦
93
≈ 14,5◦ . Somit ergibt sich der genante Wert für ψ. Teets geht
von 256◦ aus108 .
• θ0 ≈ −24,75◦
Diesen Betrag kann man aus der von Short genannten Uhrzeit des dritten Kontakts
für Beobachter in Greenwich (8:19:00) abschätzen, weil die Halbzeit des Transits
folglich etwa drei Stunden früher stattgefunden hatte. Da die Sonne ca. um 12 Uhr
mittags kulminiert, waren um 5:19 morgens noch 10,25◦ (=
41·360◦
)
60·24
zwischen dem
Nullmeridian und der Normalen zur Verbindung Ermittelpunkt – Sonne, die aufgrund
der vorhergehenden Überlegung 14,5◦ von der x-Achse entfernt war. Die zwei Winkel
addiert ergeben 24,75◦ . Bei Teets findet man −25◦109 .
• " ≈ 23,47◦
Die Neigung der Erdachse gegenüber der Ekliptik war vor 250 Jahren etwas größer
als heute und Short sicher bekannt.
Um den Winkelabstand des Nullmeridians von der x 0 -Achse zur Zeit des dritten Kontakts
(θ ) aus θ0 ± 15,041◦ /h · t zu berechnen, wird t durch die halbe Dauer des Venustransits
vom Erdmittelpunkt aus gesehen (T ) angenähert.
Die Ergebnisse für einige Orte inklusive der damals verwendeten Längen- und Breitengrade sind in Tabelle 2.5 zusammen mit den gemessenen Daten und Shorts Originalresultaten110 in Klammern, die nur geringfügig abweichen, aufgelistet. Teets Ergebnisse weichen
wegen der unterschiedlichen Parameter jeweils um einige Bogensekunden mehr von Shorts
Resultaten ab als die von mir berechneten.
Vgl. TEETS: Mathematics Magazine of the Mathematical Association of America 76 [2003], S. 345.
Vgl. ibid.
110
SHORT: Philosophical Transactions of the Royal Society 52 [1761 – 1762], S. 615.
108
109
78
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
Tab. 2.5.: Mit modernen mathematischen Methoden rekonstruierte Ergebnisse der Bestimmung der
Sonnenparallaxe nach James Short aus seinen Originaldaten (Shorts Originalergebnisse
in Klammer)
Ort
Kap
Greenwich
Rom
Stockholm
Cajaneburg
geogr. Länge
[h:min:s]
1:13:35 O
0:00:00
0:49:47 O
1:12:20 O
1:51:40 O
geogr. Breite
33◦ 550 4200 S
51◦ 280 3700 N
41◦ 530 5400 N
59◦ 200 3000 N
64◦ 130 3000 N
T̃ − T [min:s]
6:06 (6:08)
1:11 (1:11)
0:13 (0:13)
2:17 (2:18)
2:58 (2:59)
Differenz zum Kap
berechnet
beobachtet
7:17 (7:19)
6:19 (6:21)
8:23 (8:26)
9:04 (9:07)
7:15
6:26
8:25
8:56
Parallaxe
8,4600
8,6600
8,5300
8,3700
(8,4200 )
(8,6100 )
(8,4800 )
(8,3300 )
Erneutes Durchrechnen mit Shorts resultierendem Mittelwert von 8,4700 bzw. 8,5200
für die Sonnenparallaxe am Tag des Transits ergäbe keine bessere Annäherung als unter
der Verwendung der 8,500 . Vermutlich hatte Short aber zuerst andere Startwerte für das
Iterationsverfahren probiert, deren Ergebnisse aber ungefähr gegen 8,500 konvergierten.
Bei einer zweiten, leicht abgeänderten Methode verglich Short für verschiedene Orte die
beobachtete Gesamtdauer des Venustransits, also die Zeit vom zweiten bis dritten Kontakt,
mit der Gesamtdauer, die aus der hypothetischen Sonnenparallaxe von 8,500 berechnet
wurde. Genauer gesagt berechnete er einerseits die Differenz zwischen der theoretischen
Gesamtdauer vom Ermittelpunkt aus gesehen (einfach 2T ) und der theoretischen Gesamtdauer für einen realen Beobachter (also wird t durch −T angenähert, um θ aus θ0
zu berechnen und das unter Verwendung der positiven Wurzel resultierende T̃ , hier T̃−
genannt, zum bisherigen T̃ , hier T̃+ genannt, addiert). Andererseits nahm er die Differenz
zwischen der theoretischen Gesamtdauer vom Ermittelpunkt aus gesehen und der beobachteten Gesamtdauer. Anschließend setzte er die angenommene Sonnenparallaxe mit der
gesuchten ins selbe Verhältnis wie diese zwei Differenzen zueinander, also
8,500
α
=
2T − ( T̃+ + T̃− )
2T − Tbeobacht et
,
und konnte so das α bestimmen.
Dabei kam er mit Messdaten von weiteren 16 Beobachtungsorten auf ein Mittel von
9,5600 am Tag des Transits, bzw. mit Weglassen der größten 4 „Ausreißer“ auf 8,6900111 ,
bei seiner nächsten Veröffentlichung ein Jahr später mit noch mehr Messdaten kam er
schlussendlich auf eine Parallaxe von 8,5600112 , was das Ergebnis des ersten Verfahrens
recht gut bestätigte.
111
112
Vgl. SHORT: Philosophical Transactions of the Royal Society 52 [1761 – 1762], S. 618.
Vgl. SHORT, James: Second Paper concerning the Parallax of the Sun Determined from the Observations of
the Late Transit of Venus, in Which This Subject is Treated of More at Length, and the Quantity of the
Parallax More Fully Ascertained. Philosophical Transactions of the Royal Society, 53 1763, S. 340.
79
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
Andere Mathematiker und Astronomen hingegen kamen mit ähnlichen Methoden und
teilweise erst im 19. Jahrhundert auf bis zu 200 abweichende Werte. Lange akzeptiert war
das Ergebnis des deutschen Astronomen Johann Franz Encke (1791 – 1865), nämlich ca.
8,5700113 . Am nächsten am heutigen Ergebnis war das von Thomas Hornsby mit 8,7800114 und
mit verbesserten Rechenmethoden und genaueren Koordinaten das von Simon Newcomb
mit 8,8500115 .
Der Hauptgrund für die Ungenauigkeit war neben der schwierigen Bestimmung der
geographischen Länge und der etwas zu groß angesetzten Winkelgeschwindigkeit der
Venus das so genannte Tropfenphänomen (engl. black drop effect). Die Venus erscheint
nämlich kurz nach dem zweiten und kurz vor dem dritten Kontakt nicht mehr kreisrund,
sondern zum Sonnenrand hin wie ein Tropfen verformt. Die Ursache dieses Phänomens ist
allerdings nicht – wie früher behauptet – die dichte Venusatmosphäre, sondern liegt in dem
begrenzten Auflösungsvermögen der eingesetzten Teleskope. Aufgrund dieses optischen
Phänomens wich die von unterschiedlichen Personen am selben Ort für den zweiten und
dritten Kontakt genommene Zeit um mehrere Sekunden voneinander ab.
Trotz Zweifel an der erreichbaren Genauigkeit durch die Venustransitmethode wurden
auch bei den Durchgängen von 1874 und 1882 viele Expeditionen angestrengt, um die
Sonnenparallaxe zu bestimmen. Das Ergebnis war aber wiederum nicht eindeutig, wie
Simon Newcomb, einer der führenden Astronomen der damaligen Zeit, belegte:
„Die Werte, welche von den einzelnen Stationen für die Sonnenparallaxe
hergeleitet wurden, hielten sich diesmal zwischen den Grenzen 8,7600 und
8,9100 . Aus der Gesamtheit aller während der beiden Durchgänge von 1874
und 1882 ausgeführten Beobachtungen hat Newcomb einen endgültigen Wert
für die Sonnenparallaxe hergeleitet. Danach führen die heliometrischen und
photographischen Messungen zu dem Werte 8,8600 , die Kontaktbeobachtungen
dagegen zu dem wesentlich kleineren Werte 8,7900 . [...]
Es läßt sich leider nicht leugnen, daß die Ergebnisse der Venusexpeditionen dem
enormen Aufwande an Fleiß, Mühe, Kosten, zu dem sämtliche Kulturstaaten
der Erde beigetragen haben, nicht entsprechen, [...]“116
113
ENCKE, Johann Franz: Über den Venusdurchgang von 1769. Abhandlungen der Königlichen Akademie der
Wissenschaften zu Berlin, Mathematische Klasse 1835 (publ. 1837), S. 309.
114
HORNSBY, Thomas: The Quantity of the Sun’s Parallax, as Deduced from the Observations of the Transit of
Venus, on June 3, 1769. Philosophical Transactions of the Royal Society, 61 1771, S. 579.
115
NEWCOMB, Simon: Investigation of the Distance of the Sun and of the Elements which depend upon it.
Astronomical and Meteorological Observations made at the United States Naval Observatory during the
Year 1865, Appendix II. 1867, S. 29.
116
NEWCOMB, Simon; VOGEL, H. C. (Hrsg.): Popular Astronomy (dt.: Newcomb-Engelmanns populäre
Astronomie). 3. Auflage. Engelmann, 1905, S. 200.
80
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
2.3.5. Weitere Methoden
Wegen der nicht überwindbaren Ungenauigkeit des Venustransitverfahrens wandte man
sich wieder vermehrt anderen Methoden wie der Parallaxenbestimmung von Mars und
den im 19. Jahrhundert entdeckten Asteroiden zu, die im Gegensatz zu Planeten den
Vorteil bieten, dass sie keine Atmosphäre haben und nicht als Scheibe erscheinen und
deshalb genauer lokalisiert werden können. So erlangte man vor allem durch die Beiträge
des Schotten David Gill (1843 – 1914) in der zweiten Hälfte des 19. Jahrhunderts die
Einsicht, die Sonnenparallaxe sei etwa 8,800 (8,80200 ± 0,00500117 ). Besonders gut für eine
exakte Messung eignete sich der 1898 gefundene Kleinplanet Eros, der sich teilweise
zwischen Mars und Erde bewegt und sich letzterer bis zu 0,15 AE annähert. Nach der
relativ günstigen Oppositionsstellung (Erdabstand ca. 0,3 AE) im Jahr 1900 publizierte der
Engländer Arthur Robert Hinks (1873 – 1945) einen Wert von 8,80600 ± 0,00400118 . Bei der
noch geeigneteren Opposition im Jahr 1931 gab es umfassendere Beobachtungen unter
der Leitung von Harold Spencer Jones (1890 – 1960), die eine Sonnenparallaxe von ca.
8,79000119 ergaben, nach einem anderen Rechenverfahren 8,798400 ± 0,000400120 .
Neben den bisher genannten Methoden waren um 1900 aber auch noch andere zur
Bestimmung der Astronomischen Einheit bekannt:
Eine vom Prinzip her einfache basiert einerseits auf Galileos Entdeckung der Jupitermonde, die wie schon erwähnt als eine Art Ziffernblatt einer Uhr fungieren, die von weit
entfernten Punkten auf der Erde gleichzeitig gesehen werden kann und so lange Zeit
zur Navigation bzw. Vermessung diente, und andererseits auf der Endlichkeit der Lichtgeschwindigkeit. Diese vermutete zwar auch schon Galileo, konnte jedoch erst vom dänischen
Astronomen Ole Rømer (1644 – 1710) gerade anhand der Jupitermondverfinsterungen
nachgewiesen werden, die, wenn die Erde weiter von Jupiter entfernt ist, einige Minuten später beobachtet wurden als dem Rhythmus weniger Monate zuvor entsprechend
vorherberechnet.
Da die Lichtgeschwindigkeit im Laufe des 19. Jahrhunderts durch terrestrische Versuche
wie die Zahnrad- oder Drehspiegelmethode und zuvor schon durch die von Bradley auf der
Suche nach einer messbaren Sternparallaxe zwischen 1725 und 1728 entdeckte jährliche
Aberration des Lichtes (s. Abschn. 3.2.2) auf 1% genau bestimmt war, konnte man das
117
GILL, David: Determination of the Solar Parallax, &c. vol. I., part 6. Combination of Results and General
Conclusions. Annals of the Cape Observatory, 6 1897, S. 29.
118
HINKS, Arthur Robert: Solar parallax papers. Monthly Notices of the Royal Astronomical Society, 70 1910,
S. 603.
119
SPENCER JONES, Harold: Meeting of the Royal Astronomical Society. The Observatory, 64 1941, Nr. 803,
S. 104.
120
RABE, Eugene: Additional note on the solar parallax from Eros. Astronomical Journal, 59 1954, S. 410.
81
2.3. NEUZEIT
Zweite Sprosse: Das Sonnensystem
Verfahren Rømers umkehren und die Astronomische Einheit aus derjenigen Zeit berechnen,
die das Licht für die Strecke, die der Entfernung der Erde von der Sonne gleichkommt,
benötigt. Aus der ermittelten so genannten Lichtzeit von 8 Minuten 18,5 Sekunden und
der Lichtgeschwindigkeit von etwas weniger als 300 000 Kilometern pro Sekunde (wie sie
um 1900 bekannt war) folgt eine Entfernung von ca. 149,45 Millionen Kilometern, die
einer Parallaxe von 8,80300 entspricht121 .
Andere Verfahren sind mehr theoretischer Art: Der französische Mathematiker Urbain
Le Verrier (1811 – 1877) – berühmt für die Berechnung der Neptunbahn, die mit Hilfe
von Störungen im Umlauf des Uranus ermittelt wurde und 1846 zu seiner Entdeckung
führte (Uranus wurde schon 1781 zufällig von Wilhelm Herschel entdeckt) – bestimmte
die Sonnenparallaxe über Bahnstörungen des Venus- und Marsorbits, aus denen auf die
Erdmasse geschlossen werden konnte, zu 8,86600122 .
Eine weitere Methode basiert auf dem gravitativen Einfluss der Sonne auf den Mond,
durch den folgende Ungleichheit in der Bewegung des Mondes hervorgerufen wird: Im
ersten Viertel bleibt der Mond etwa 20 hinter seinem mittleren Ort zurück, während er
in der Nähe des letzten Viertels seinem mittleren Ort ebensoviel vorauseilt. Aus dieser
so genannten parallaktischen Ungleichheit des Mondes konnte sogar anfangs der Wert
8,87400 ± 0,01600123 für die Sonnenparallaxe gewonnen werden (später jedoch z.B. auf
8,76124 korrigiert).
Die Ergebnisse für die Sonnenparallaxe schwankten also in der zweiten Hälfte des 19.
und ersten Hälfte des 20. Jahrhunderts um den Wert 8,8000 , die Entfernung der Sonne also
um 149,5 Millionen Kilometer. „Eine Hundertstel Bogensekunde Änderung in der Parallaxe
entspricht aber 170 000 km Änderung in der Entfernung, so daß wir mit einer Unsicherheit
von einigen Hunderttausend Kilometern in der Sonnenentfernung rechnen müssen.“125
121
Vgl. NEWCOMB, Simon: Simon Newcombs Astronomie für jederman. 2. Auflage. Fischer, 1910, S. 237ff..
LE VERRIER, Urbain: Sur les masses des planètes et la parallaxe du Soleil. Comptes rendus hebdomadaires
des séances de l’académie des sciences, 75 1872, S. 169.
123
BATTERMANN, Hans Felix Heinrich: Beiträge zur Bestimmung der Mondbewegung und der
Sonnenparallaxe aus Beobachtungen von Sternbedeckungen am sechsfüßigen Merz’schen Fernrohr der
Berliner Sternwarte. Beobachtungs-Ergebnisse der Königlichen Sternwarte zu Berlin, 5 1891, S. 40.
124
COWELL, Philip Herbert: Moon, semi-diameter, parallactic inequality, and variation of the, from Greenwich
meridian observations. Monthly Notices of the Royal Astronomical Society, 64 1903, S. 97.
125
Vgl. NEWCOMB: Popular Astronomy, S. 204.
122
82
2.4. HEUTE
Zweite Sprosse: Das Sonnensystem
2.4. Heute
Fortschritte in der Messgenauigkeit wurden ab den 60er Jahren des 20. Jahrhunderts durch
den Einsatz von Radargeräten erzielt. Dabei werden Radiowellen zu den Planeten Merkur,
Venus und Mars geschickt und die Zeit bis zum Empfang des reflektierten Signals gemessen.
Die daraus errechnete mittlere Parallaxe der Sonne beträgt ca. 8,79400 , einer mittleren
Entfernung von ca. 23 455 Erdradien bzw. ca. 149,598 Millionen Kilometern entsprechend.
Nach demselben Prinzip funktioniert die Berechnung aus von Raumsonden gesendeten
Signalen, wie es beispielsweise im Zuge der Viking- oder Pathfindermission zum Mars
durchgeführt wurde.
Heute kann die Astronomische Einheit auf wenige Meter genau angegeben werden und
ihr Wert bewegt sich neuesten Messungen zufolge um 149 597 870 700 Meter126 , was mit
einem Äquatorradius von 6 378 137 Meter einer Parallaxe von 8,794 14400 entspricht. Man
nimmt aber an, dass sich dieser Wert um 5 bis 15 Meter pro Jahrhundert verändert.
In Tabelle 2.6 sind die wichtigsten Resultate für die Sonnenparallaxe bzw. die Sonnenentfernung noch einmal zusammengefasst.
Tab. 2.6.: Historische Entwicklung der Einschätzung der Astronomischen Einheit
Zeit
Person
bis 1600
um 1620
um 1650
nach 1672
nach 1762
nach 1769

um 1900






nach 1931
nach 1960
126
bis Kepler
Kepler
Wendelin
Flamsteed
Cassini
u. a. Short
u. a. Encke
u. a. Le Verrier
u. a. Newcomb
u. a. Gill
u. a. Battermann
u. a. Spencer Jones
Methode
Parallaxe
Dichotomie/Eklipsendiagr.
u. a. Numerologie
u. a. Dichotomie
Marsparallaxe
Marsparallaxe
Venustransit
Venustransit
Bahnstörungen
Venustransit
Mars-/Asteroidenparallaxe
Lichtgeschwindigkeit
Mondbahn
Erosparallaxe
Radarmessungen
ca. 30
ca. 10
ca. 1500
< 1000
ca. 9,500
00
8,5 – 10,500
00
00
 8,5 – 8,9



AE
[Erdradien]
ca. 1 200
ca. 3 500
ca. 14 000
ca. 21 000
ca. 22 000
ca. 22 000
ca. 24 000
ca. 8,800
ca. 23 500
8,79000 – 8,79800
ca. 8,79400
ca. 23 450
ca. 23 455



STANDISH, E. Myles: The Astronomical Unit now. Proceedings of the International Astronomical Union,
2004, Nr. 196, S. 173.
83
3. Dritte Sprosse: Nahe Sterne
Nach dem Erdradius und der Astronomischen Einheit folgen die nahen Sterne als nächste
Sprosse der Entfernungsleiter, wobei „nahe“ nur im Vergleich zu noch viel weiter entfernten
Sternen verstanden werden darf; denn auch der uns am nächsten liegende Stern Proxima
Centauri befindet sich etwa 268 000 AE weit weg.
3.1. Abschätzungen bis ins 19. Jahrhundert
Da diese unvorstellbar großen Distanzen nur schwer zu messen sind, unterlagen sie bis ins
19. Jahrhundert fast ausnahmslos Spekulationen. Außerdem waren fast alle Gelehrten bis
in die frühe Neuzeit inklusive Kopernikus und Kepler vom Irrglauben überzeugt, dass sich
alle Fixsterne auf einer Sphäre geringer Dicke befinden – also etwa im selben Abstand vom
Mittelpunkt des Universums, sei dies nun die Erde oder die Sonne.
Der große Unterschied zwischen geo- und heliozentrischem Weltbild ist jedoch, dass
letzteres den Fixsternen jährliche Parallaxen vorhersagt. Dabei handelt es sich um scheinbare Veränderungen der Sternpositionen aufgrund der Bewegung der Erde um die Sonne
(s. Abb. 3.1). Diese Positionsveränderungen verlaufen je nach ekliptikaler Breite des jeweiligen Sterns entlang einer unterschiedlich geformten Ellipse, wobei für Sterne an den
p
1 AE
Erdbahn
Stern
p
Sonne
Abb. 3.1.: Als (jährliche) Sternparallaxe (π) versteht man analog zur horizontalen Parallaxe der
Sonne, bei der der Erdradius als Basislinie dient, den maximalen Winkel, unter dem die
Strecke Erde – Sonne innerhalb eines Jahres vom Stern aus gesehen wird. Dieser Winkel
entspricht gleichzeitig jenem, unter dem man von der Erde aus die große Halbachse
der Ellipse sieht, auf der sich der Stern zu bewegen scheint. Weiß man den Wert der
jährlichen Sternparallaxe, kann man – wiederum analog zur horizontalen Parallaxe der
Sonne – die Entfernung des Sterns (d) aus der einfachen trigonometrischen Beziehung
sin π = 1 dAE ausrechnen (für kleine Winkel: sin π ≈ π [rad]).
84
3.1. ABSCHÄTZUNGEN BIS INS 19. JAHRHUNDERT
Dritte Sprosse: Nahe Sterne
Ekliptikpolen und direkt in der Ekliptik die Extremfälle einer Ellipse auftreten, nämlich
Kreise bzw. Strecken.
Die Unauffindbarkeit von Sternparallaxen wurde von Gegnern des heliozentrischen
Modells schon zu Aristarchs Zeiten, später aber auch von Tycho, als Argument für eine fix
stehende Erde verwendet. Von seinen Anhängern hingegen wurde sie als Hinweis für die
sehr große Distanz zu den Sternen gedeutet.
Nach der kopernikanischen Wende und der Erfindung des Teleskops setzte sich langsam
die Ansicht durch, dass es sich bei Sternen um weit entfernte Sonnen handle, die über
einen unendlichen Raum verteilt sind.
Schon Galilei begriff, dass diese Hypothese zugleich die Möglichkeit in Aussicht stellte,
eine im Laufe des Jahres variierende Parallaxendifferenz zwischen Sternen zu messen, die
zwar auf der Himmelssphäre nebeneinander zu liegen scheinen, sich tatsächlich jedoch
weit von einander entfernt befinden („relative Parallaxe“; s. Abb. 3.2 & vgl. Abb. 2.17, sowie
Abschn. 0.1: Bewegungsparallaxe, Querdisparität).
weit entfernte Sterne
naher Stern
2p
Sonne
Erdbahn
Abb. 3.2.: Relative (jährliche) Sternparallaxe. Aus der Positionsänderung des nahe gelegenen Sterns
im Laufe eines Jahres relativ zu weit entfernten Sternen lässt sich die jährliche Sternparallaxe einfacher als durch eine absolute Messung bestimmen, falls die Parallaxe der
Hintergrundsterne vernachlässigbar klein ist.
Bis eine solche Parallaxe jedoch festgestellt werden konnte, vermochte man nur eine
Mindestentfernung anzugeben, die infolge der immer exakter werdenden Messinstrumente
immer größer wurde. Die tatsächlichen Zahlenwerte wurden jedoch lange nicht einmal
annähernd erreicht.
85
3.1. ABSCHÄTZUNGEN BIS INS 19. JAHRHUNDERT
Dritte Sprosse: Nahe Sterne
Manch ein Astronom versuchte sich auch im Messen des Winkeldurchmessers von
Sternen, was jedoch aufgrund der immensen Entfernungen auch heute noch nur indirekt
möglich ist und deshalb zu widersprüchlichen Ergebnissen führte1 .
Eng verbunden mit der Ansicht, dass die Sterne über den Raum verteilt sind, war der
Gedanke, dass alle Sterne inklusive der Sonne in Wahrheit etwa gleich groß sein und
gleich hell leuchten könnten und somit fast ausschließlich aufgrund ihrer unterschiedlichen Entfernungen so unterschiedlich hell erscheinen; kurz gesagt: Helle Sterne sind uns
näher (vgl. Abschn. 0.1: Scheinbare Helligkeit). Basierend auf dieser Annahme konnten
ab dem Ende des 17. Jahrhunderts erstmals Angaben von Sterndistanzen in der richtigen
Größenordnung gemacht werden.
Eine der ersten vernünftigen Abschätzungen gelang Isaac Newton folgendermaßen:
„Die Scheibe des Saturn, deren Durchmesser nur 1700 oder 1800 ist, erhält
bloß etwa
1
2 100 000 000
vom Licht der Sonne; denn um so viel weniger ist diese
Scheibe als die ganze sphärische Oberfläche der Kugel des Saturn. Wenn
wir nun annehmen, Saturn reflektiert etwa
1
4
von diesem Licht, wird das
ganze Licht, das von seiner beleuchteten Hemisphäre reflektiert wird, etwa
1
4 200 000 000
vom ganzen von der Hemisphäre der Sonne ausgestrahlten Licht sein;
und deswegen, weil Helligkeit im doppelten Verhältnis der Entfernung vom
p
leuchtenden Körper abfällt, würde, wenn die Sonne 10 000 · 42-mal weiter
entfernt wäre als Saturn, sie noch so klar erscheinen wie Saturn es nun ohne
seine Ringe tut, das ist etwas heller als ein Fixstern der ersten Größenklasse.
Lasst uns deshalb annehmen, dass die Entfernung, von der aus die Sonne als
ein Fixstern scheinen würde, etwa 100 000-mal größer wäre als die des Saturn,
und ihr scheinbarer Durchmesser würde 7v 16vi [≈ 0,000 03400 ; v steht für 60−5 ;
vgl. Sexagesimalsystem von Ptolemäus in Abschn. 2.1.4] sein und ihre aus der
jährlichen Bewegung der Erde hervorgehende Parallaxe 130000 [≈ 0,003600 ]: und
so groß wird die Entfernung, der scheinbare Durchmesser und die Parallaxe
eines Fixsterns der ersten Größenklasse sein, der in Größe und Helligkeit gleich
unserer Sonne ist.“2
Er rechnete sich also das Verhältnis der Querschnittsfläche des Saturns zur Gesamtoberfläche einer Kugel mit dem Saturnabstand zur Sonne als Radius (R) aus, indem er von einem
1
Vgl. FERNIE, J. D.: The Historical Search for Stellar Parallax. Journal of the Royal Astronomical Society of
Canada, 69 1975, Nr. 4, S. 153ff.
2
Frei übersetzt nach NEWTON, Isaac; MOTTE, Andrew (Hrsg.): Newton’s Principia: The Mathematical
Principles of Natural Philosophy. To which is added Newton’s System of the World. D. Adee, 1848, S. 547
(Originaltext im Anhang).
86
3.1. ABSCHÄTZUNGEN BIS INS 19. JAHRHUNDERT
Dritte Sprosse: Nahe Sterne
Sehwinkel von ca. 900 ausging, unter dem der Saturnradius (r) von der Sonne aus gesehen
wird:
r 2π
2
4R π
≈
1
,
2,1 · 109
wobei
r
R
≈ sin(900 ).
Mit einem geschätzten Rückstrahlvermögen, der so genannten „Albedo3 “, von
1
4
(in Wahr-
heit fast doppelt so groß) und der Tatsache, dass Saturn nur von der ihm zugewandten
Hälfte der Sonne beschienen wird, kommt Newton auf den angegebenen Wert:
1
4
·
r 2π
1
4R2 π
2
≈
1
4,2 · 109
.
Weil die Lichtintensität indirekt proportional zum Entfernungsquadrat abfällt, ergibt sich
für die Entfernung eines sonnenähnlichen Sterns, der gleich hell erschiene wie Saturn,
p
mindestens die 42 · 104 -fache (≈ 65 000) Saturnentfernung von der Erde, für sonnenähnliche Sterne der ersten Größenklasse, also etwas weniger hell als Saturn, die geschätzte
100 000-fache Saturnentfernung.
Die Größenklasse, auch Magnitude genannt (Einheitenzeichen mag), ist ein Maß für die scheinbare
Helligkeit eines Himmelsobjekts (im für das menschliche Auge sichtbaren Wellenlängenbereich). Diese auf
der Sinnesempfindung des Auges basierende Skala geht auf Hipparch zurück und wird auch heute noch
verwendet. Die Magnitude gibt also an, wie hell ein Himmelskörper einem Beobachter auf der Erde erscheint,
wobei kleinere Zahlen für hellere Objekte stehen. Nach der Sonne mit −26,72 mag ist Sirius mit −1,43 mag
der zweithellste Stern am Himmel, gefolgt von Canopus (−0,72 mag), Arcturus (−0,04 mag; variabel), α
Centauri A (−0,01 mag) und Wega (0,03 mag)4 . Unter Großstadtbedingungen erkennt man mit dem bloßen
Auge oftmals nur Sterne bis zur vierten Größenklasse, im Gebirge hingegen unter Idealbedingungen bis
7 mag.
Für die Entfernung Erde – Saturn verwendete Newton 9,5 AE, was mit 320 für den
Winkeldurchmesser der Sonne aus 1 AE Entfernung etwa den Wert 0,0020200 für den
Winkeldurchmesser einer in 950 000 AE Entfernung liegenden Sonne ergibt (entspricht ca.
70000 16v in Newtons Sexagesimalschreibweise). Für die Parallaxe erhält man so ca. 0,2200
(entspricht ca. 13000 in Newtons Sexagesimalschreibweise). Im Originaltext findet man
stattdessen 7v 16vi bzw. 130000 , also eine falsche sexagesimale Stelle.
Tatsächlich würde die Sonne in einer Entfernung von etwa 350 000 AE ein Stern erster
Größenklasse sein, was einer Parallaxe von ca. 0,5900 entspräche.
Newtons Vorgehensweise ähnelt stark dem heute für einen großen Teil der Sterne verwendeten Verfahren zur Entfernungsmessung: der so genannten „fotometrischen Parallaxe“.
Der einzige große Unterschied besteht darin, dass dabei Sterne nach ihrem Spektrum in vie3
4
lat. albus „weiß“
Vgl. CDS: SIMBAD database. simbad.u-strasbg.fr – Zugriff am 27.09.2008.
87
3.2. NEBENPRODUKTE
Dritte Sprosse: Nahe Sterne
le verschiedene Sternklassen eingeteilt werden. Die absoluten Entfernungen von einzelnen
Vertretern jeder Sternklasse mussten jedoch auf andere Weise gefunden werden.
3.2. Nebenprodukte
Zwar konnten, wie gesagt, bis zum Anfang des 19. Jahrhunderts keine Sternparallaxen gemessen werden, dennoch wurden beiläufig große Fortschritte bezüglich des Verständnisses
und der Beobachtung von Sternen erzielt:
3.2.1. Die Eigenbewegung von Sternen
Einer dieser Fortschritte gelang 1718 Edmond Halley beim Vergleich von aktuellen Ortsangaben von Sternen mit den Aufzeichnungen der antiken Griechen und denen von Tycho.
Er stellte fest, dass sich die Positionen von einigen „prominenten“ Sternen wie Sirius,
Betelgeuse, Aldebaran und Arcturus über die Jahrhunderte bis um einem halben Grad
verändert hatten. Diese Abweichungen erschienen ihm zu groß, um sie für Messungenauigkeiten zu halten – auch wenn die Griechen noch keine Teleskope besaßen. Deshalb zog
Halley den Schluss, dass die so genannten Fixsterne gar nicht fix waren, sondern eine
Eigenbewegung vollziehen. Diese Erkenntnis widersprach endgültig der Theorie einer
dünnen Himmelssphäre, in der sich alle Sterne befinden5 .
Eine Folgerung daraus war, dass Sterne mit großer Eigenbewegung dem Sonnensystem
tendenziell näher liegen und sich daher besser für Parallaxenmessungen eignen würden.
3.2.2. Die Aberration des Lichts und die Nutation der Erdachse
James Bradley (1693 – 1762) begab sich durch Messung der Zenitdistanz eines Sterns beim
Meridiandurchgang aus der Neigung des Fernrohrs gegen ein feines Lot auf die Suche
nach einer Sternparallaxe. Dabei entdeckte er zwischen 1725 und 1728 geringe jährliche
Winkelschwankungen von etwa 2000 bei der Deklination des Sterns γ Draconis. Solche
periodische Winkelabweichungen waren schon früher von einflussreichen Astronomen
wie Hooke, Cassini, Flamsteed und Rømer beobachtet, aber nicht richtig erklärt worden6 .
Die Refraktion in der Erdatmosphäre kann vernachlässigt werden, weil γ Draconis in
5
Vgl. HALLEY, Edmond: Considerations on the Change of the Latitudes of Some of the Principal Fixt Stars.
Philosophical Transactions of the Royal Society, 30 1717 – 1719, S. 736ff.
6
Vgl. HERRMANN, Dieter B.: Kosmische Weiten – Kurze Geschichte der Entfernungsmessung im Weltall.
3. Auflage. Deutsch, 1990, S. 26ff.
88
3.2. NEBENPRODUKTE
Dritte Sprosse: Nahe Sterne
Südengland praktisch durch den Zenit wandert. Die Schwankungen passten aber auch
weder zeitlich noch von der Größenordnung zu einer Parallaxe.
Angeblich hatte Bradley bei einer Segelfahrt auf der Themse den rettenden Einfall, als er
die Windfahne des Bootes beobachtete. Eine solche zeigt während der Fahrt wegen der Eigengeschwindigkeit des Schiffs nicht die tatsächliche sondern die scheinbare Windrichtung
an und ändert somit bei jeder Kursänderung des Bootes auch geringfügig die angezeigte
Himmelsrichtung, aus der der Wind bläst. Als Segelboot dachte sich Bradley nun die Erde,
als Wind das Sternenlicht, als Kursänderung die jährliche Bewegung der Erde um die
Sonne7 und als Windfahne sein Teleskop. Mit dieser Erklärung für das Phänomen, das
heute Aberration8 genannt wird, konnte er erstens die schon von Rømer nachgewiesene
Endlichkeit der Lichtgeschwindigkeit bestätigen und dessen Abschätzung erheblich verbessern, zweitens Tychos Weltbild einer ruhenden Erde endgültig falsifizieren und drittens
einen nicht zu vernachlässigen Beitrag zur Genauigkeit von Sternpositionen und somit zur
Parallaxenmessung liefern.
Weiters schloss Bradley aus seiner Messgenauigkeit, dass die Sternparallaxen kleiner als
eine Bogensekunde sein müssten.9
Zusätzlich zur Aberration veröffentlichte Bradley 1748 die Entdeckung von Winkelschwankungen bei Sternpositionen in derselben Größenordnung wie durch die Aberration,
jedoch in einem ca. 19-jährigen Zyklus. Seine Erklärung dafür war der gravitative Einfluss der Präzessionsbewegung der Mondbahn auf die Präzession der Erde. Denn dieser
äußert sich in einer leichten periodischen „Nickbewegung“ der Erdachse: der so genannten
Nutation.10
3.2.3. Doppelsterne
Auf der Suche nach Sternparallaxen mit Galileis Methode setzte sich der deutsch-britische
Astronom Friedrich Wilhelm Herschel (1738 – 1822), berühmt für die Entdeckung des
Uranus, in der zweiten Hälfte des 18. Jahrhunderts mit Doppelsternen auseinander. So
werden Sterne genannt, die nur wenige Bogensekunden voneinander – also großteils nur
mit Teleskop – getrennt am Himmel zu sehen sind. Über 70 davon wurden erstmals vom
7
Neben der hier beschriebenen jährlichen Aberration sind heute auch die viel kleinere tägliche, also aufgrund
der täglichen Erdrotation, und die säkulare Aberration aufgrund der Bewegung des kompletten
Sonnensystems bekannt.
8
lat. aberratio „Ablenkung“
9
Vgl. BRADLEY, James: A Letter to Dr. Edmond Halley Astronom. Reg. &c. giving an Account of a new
discovered Motion of the Fix’d Stars. Philosophical Transactions of the Royal Society, 35 1727 – 1728, S. 660.
10
Vgl. BRADLEY, James: A Letter to the Right honourable George Earl of Macclesfield concerning an apparent
Motion observed in some of the fixed Stars. Philosophical Transactions of the Royal Society, 45 1748, S. 13.
89
3.3. DIE ERSTEN GEMESSENEN STERNPARALLAXEN
Dritte Sprosse: Nahe Sterne
deutschen Astronomen Christian Mayer (1719 – 1783) systematisch beobachtet und 1779
katalogisiert11 . Er hielt diese Objektpaare, wie schon der englische Naturphilosoph John
Michell (1724 – 1793) aus wahrscheinlichkeitstheoretischen Gründen12 , auch physikalisch
für zusammengehörend. Herschel, der in den darauf folgenden Jahren hunderte weitere
solcher Doppelsterne entdeckte13 , vermutete hingegen, dass insbesondere Doppelsterne
mit unterschiedlicher Helligkeit in Wahrheit weit auseinander lägen und sich deshalb für
die Messung einer relativen Parallaxe eigneten14 . Um 1800 wies er jedoch selbst für einige
Doppelsternsysteme die Theorie Mayers und Michells nach, indem er eine gemeinsame
Eigenbewegung und Drehung um den gemeinsamen Schwerpunkt feststellte. Diese Kandidaten eigneten sich folglich zwar nicht zur Messung einer relativen Parallaxe, jedoch
hatte Herschel dadurch den Beweis für die Existenz „echter“ Doppelsterne erbracht, die
später beispielsweise für das Messen von Sternmassen mit Hilfe von Newtons Verallgemeinerung des dritten keplerschen Gesetzes äußerst nützlich wurden (oder umgekehrt zur
Entfernungsmessung mittels sog. „dynamischer Parallaxe“). Eine relative Sternparallaxe
vermochte er jedoch – auch bei den „unechten“ Doppelsternen – nicht zu messen.15 16
3.3. Die ersten gemessenen Sternparallaxen
Seit Ende des 17. Jahrhunderts glaubten die angesehensten Astronomen ihrer Zeit, mit immer aufwändigeren und exakteren Instrumenten den Wert einer Sternparallaxe und somit
die Entfernung zu einem Gestirn vermeintlich gefunden zu haben. Aber jedes Mal mussten ihre Ergebnisse wegen Messfehlern oder oben erwähnter neu entdeckter Phänomene
revidiert werden.
Erst gegen Ende der 1830er Jahre gelang drei Astronomen fast gleichzeitig und unabhängig voneinander die Messung einer Sternparallaxe. Die Ehre des Ersten wird im Allgemeinen
dem Deutschen Friedrich Wilhelm Bessel (1784 – 1846) zugesprochen, weil sein Ergebnis
die Fachwelt überzeugte und die Abweichung vom heutigen Wert am geringsten ist.
11
MAYER, Christian: De novis in coelo sidereo phaenomenis in miris stellarum fixarum comitibus Mannhemii.
Typ. Elector Aulica & Academica, 1779.
12
Vgl. MICHELL, John: An Inquiry into the Probable Parallax, and Magnitude of the Fixed Stars, from the
Quantity of Light Which They Afford us, and the Particular Circumstances of Their Situation. Philosophical
Transactions of the Royal Society, 57 1767.
13
HERSCHEL, Friedrich Wilhelm: Catalogue of Double Stars. Philosophical Transactions of the Royal Society,
72 1782.
14
Vgl. HERSCHEL, Friedrich Wilhelm: On the Parallax of the Fixed Stars. Philosophical Transactions of the
Royal Society, 72 1782.
15
Vgl. HERRMANN: Kosmische Weiten, S. 30ff.
16
Vgl. LOVELL: Das unendliche Weltall, S. 109f.
90
3.3. DIE ERSTEN GEMESSENEN STERNPARALLAXEN
Dritte Sprosse: Nahe Sterne
Am Anfang seiner Veröffentlichung beschrieb er den Status quo und die Auswahlkriterien
für die für eine Parallaxenmessung in Frage kommenden Sterne:
„Bei dem jetzigen Zustande unserer Kenntnisse des Weltgebäudes können
wir nur zwei, in der That nicht sichere Gründe der Vermuthung, daß ein
Fixstern verhältnißmäßig nahe sei, anführen; nämlich den optischen Grund,
seine ausgezeichnete Helligkeit, und den geometrischen, seine ausgezeichnet
starke eigene Bewegung. Daß beide täuschen können, ist nicht zu bezweifeln;
allein wenn eine Untersuchung über die jährliche Parallaxe eines Fixsterns
unternommen werden soll, so sind sie dennoch die einzigen, welche seine Wahl
leiten können.“17
Bessel gab aufgrund von vorangegangen Beobachtungen, wonach ein großer Teil von
Sternen mit großer Eigenbewegung relativ schwach leuchtete, dem zweiten Kriterium eine
höhere Gewichtung und wählte trotz seiner geringen scheinbaren Helligkeit den Stern 61
Cygni für seine Messungen. Von diesem hatte er die damals größte bekannte Eigenbewegung von über 500 pro Jahr gemessen. Außerdem war das Objekt ein Zirkumpolarstern, also
das ganze Jahr über beobachtbar, und es befanden sich zwei geeignete Vergleichssterne
in unmittelbarer Nähe, von denen er aufgrund fehlender Eigenbewegung und geringer
Helligkeit berechtigterweise eine viel größere Entfernung annehmen konnte.
Nach vielen Beobachtungen über mehrere Jahre und gewissenhafter Reduktion der
Daten veröffentlichte er 1838 sein Ergebnis: eine jährliche Parallaxe von 0,313600 ± 0,020200
bzw. eine Entfernung von 657 700 AE18 . Heute geht man von 0,28700 bzw. 718 400 AE aus,
was bedeutet, dass Bessel sich um knapp 10 % geirrt hat.
Über ein Jahr vor Bessels Veröffentlichung hatte schon der deutsche Astronom Friedrich
Georg Wilhelm Struve (1793 – 1864) eine Sternparallaxe entdeckt. Bei der Wahl eines
geeigneten Sterns bevorzugte er das Kriterium der scheinbaren Helligkeit und entschied sich
deshalb für einen der hellsten Sterne der nördlichen Hemisphäre, nämlich Wega (α Lyrae).
Aus 17 im Zeitraum von zwei Jahren gemessenen Positionen relativ zu einem günstigen
Nachbarobjekt berechnete er die Parallaxe 0,12500 ± 0,05500 , fast genau dem heutigen Wert
entsprechend. Struve versprach jedoch weitere Messungen, um die Genauigkeit zu erhöhen,
was die Glaubwürdigkeit seiner Ergebnisse in Frage stellen ließ.19 1840 publizierte er dann
17
BESSEL, Friedrich Wilhelm: Bestimmung der Entfernung des 61sten Sterns des Schwans. Astronomische
Nachrichten, 16 1839, Nr. 366, S. 65f.
18
Ibid., S. 93.
19
Vgl. HERRMANN: Kosmische Weiten, S. 39f.
91
3.3. DIE ERSTEN GEMESSENEN STERNPARALLAXEN
Dritte Sprosse: Nahe Sterne
den schlechteren Wert 0,261300 ± 0,02540020 , weshalb er heute in den Geschichtsbüchern
wohl im Schatten Bessels steht.
Viel entscheidender als diese Reihung ist, dass die beiden Messungen erst durch die
Fernrohre des bayerischen Optikers und Physikers Joseph von Fraunhofer (1787 – 1826)
ermöglicht wurden, der es als erster verstand, größere Teleskope so zu bauen, „dass
der Vortheil des mikrometrischen Messens nicht mehr durch früher damit verbundene
Nachtheile überwogen wurde.“21
Noch vor Bessel und Struve führte Anfang der 1830er der schottische Astronom Thomas
Henderson (1798 – 1844) in der Sternwarte am Kap der guten Hoffnung ohne hervorragende Instrumente absolute Messungen von Sternpositionen durch, die eigentlich nicht die
Bestimmung einer Parallaxe als Ziel hatten.
Unter den von ihm beobachteten Objekten befand sich auch der Doppelstern α Centauri,
der hinsichtlich seiner scheinbaren Helligkeit den dritten Rang unter allen Fixsternen
einnimmt. Dass α Centauri zu den nächsten Sternen gehören musste, „ging nicht allein
aus seiner großen scheinbaren Helligkeit hervor. Vielmehr erbrachten die Beobachtungen
dieses Sterns auch die erstaunlich große Eigenbewegung von 3,600 pro Jahr. Außerdem
handelte es sich um ein Doppelsternsystem mit der relativ kurzen Umlaufzeit von 80
Jahren, woraus auf einen geringen Abstand der beiden Komponenten geschlossen werden
musste. Im Winkelmaß betrug dieser trotzdem 1500 !“22
Als Henderson seine Beobachtungsdaten von α Centauri auf eine Parallaxe hin untersuchte, fand er noch vor Bekanntwerden von Bessels und Struves Ergebnissen den Wert
1,1600 ± 0,110023 . Er publizierte sein Resultat jedoch erst einige Wochen nach Bessel, weil
er es eigentlich noch durch weitere Messungen bestätigen wollte, letztlich aber doch von
Bessels Errungenschaft ermutigt wurde.
Das Doppelsternsystem α Centauri galt bis zur Entdeckung seines unscheinbaren Nachbarn Proxima Centauri als das erdnächste Objekt. Seine Parallaxe wird heute mit etwa
0,7500 beziffert, einer Entfernung von ca. 274 000 AE entsprechend (zum Vergleich die
Werte für Proxima Centauri: ca. 0,7700 bzw. 267 000 AE). Hendersons Abschätzung war also
nicht besonders genau.
20
STRUVE, Friedrich Georg Wilhelm: Über die Parallaxe des Sterns α Lyrae nach Micrometermessungen am
großen Refractor der Dorpater Sternwarte. Astronomische Nachrichten, 17 1840, Nr. 396, S. 178.
21
BESSEL, Friedrich Wilhelm; SCHUMACHER, H. C. (Hrsg.): Populäre Vorlesungen über wissenschaftliche
Gegenstände. Perthes-Besser & Mauke, 1848, S. 245.
22
HERRMANN: Kosmische Weiten, S. 41.
23
HENDERSON, Thomas: On the Parallax of α Centauri. Monthly Notices of the Royal Astronomical Society, 4
1839, Nr. 19, S. 169.
92
3.4. HEUTE
Dritte Sprosse: Nahe Sterne
In den darauf folgenden Jahrzehnten konnte die Parallaxe nur von wenigen dutzend
Sternen hinreichend genau ermittelt werden. Um die Jahrhundertwende waren es gerade
um die hundert. Fotografische Methoden, die am Ende des 19. Jahrhunderts ihren Einzug
hielten, ermöglichten bis in die 30er Jahre des 20. Jahrhunderts die Messung von einigen
tausend Sternparallaxen. Auch der Einsatz von immer größeren Teleskopen konnte diese
Zahl jedoch nicht mehr deutlich steigern, weil das Licht eines Sterns durch die unterschiedlichen Brechungsindizes in der Erdatmosphäre immer leicht abgelenkt wird und er
deswegen verschwommen erscheint. Deshalb ist die Messgenauigkeit irdischer Teleskope
begrenzt.
3.4. Heute
Erst der Einsatz eines Weltraumteleskops konnte die Zahl der Sterne, deren Entfernungen
durch Parallaxenmessungen gefunden wurden, beträchtlich erhöhen. Nach jahrelanger Vorbereitung wurde im August 1989 HIPPARCOS (High Precision Parrallax Collecting Satellite)
an Bord einer Ariane-Rakete vom Weltraumbahnhof der ESA in Korou (Französisch-Guyana)
gestartet. Obwohl der Satellit wegen Antriebsproblemen seine geplante Umlaufbahn zwar
nicht erreichte, übertrafen die Messungen dennoch alle Erwartungen. Man war in der
Lage, die Positionen von über 100 000 Sternen mit einer Genauigkeit von etwa 0,00100 zu
bestimmen, mit einem zweiten Instrument wurden sogar über 1 000 000 Sterne auf 0,0200
genau vermessen. Für 22 396 Sterne errechnete man die Entfernung mit höchstens 10 %
Unsicherheit, wobei Distanzen bis zu 19 000 000 AE festgestellt werden konnten.
Dies umfasst zwar mehr als die ca. 5 000 – 6 000 Sterne, die mit freiem Auge sichtbar
sind, stellt aber andererseits nur einen Bruchteil der vielen Milliarden Himmelsobjekte dar,
die heutzutage schon mit modernen Teleskopen erfasst wurden. Zwar soll die Messgenauigkeit mit geplanten Nachfolgemissionen wie GAIA (Global Astrometric Interferometer for
Astrophysics) noch erheblich verbessert werden, jedoch ist klar, dass die Möglichkeiten
dieser Messmethode begrenzt sind. Denn je weiter ein Stern entfernt ist, umso größer wird
der relative Fehler, verursacht durch die Messunsicherheit. Wenn beispielsweise eine Sternparallaxe von 0,0100 gemessen wird, entsprechend einer Entfernung von fast 21 000 000 AE,
und die Messunsicherheit bei ±0,00200 liegt, bedeutet das, dass der wahre Wert der Parallaxe wahrscheinlich zwischen 0,00800 und 0,01200 liegt – die Entfernung also zwischen
ca. 17 000 000 AE und fast 26 000 000 AE beträgt. Diese Spanne kommt einer Unsicherheit
von ca. 20 % gleich. Für größere Distanzen müsste man also die Messgenauigkeit deutlich
erhöhen, was irgendwann an technische Grenzen stößt. Deshalb war man gezwungen,
93
3.4. HEUTE
Dritte Sprosse: Nahe Sterne
für den Großteil der Himmelsobjekte neue Methoden zur Entfernungsbestimmung zu
entwickeln, die jedoch nur mehr bedingt auf geometrischen Mitteln beruhen.
Wie bei obigen Entfernungsangaben ersichtlich, eignet sich die Astronomische Einheit
quasi nur für die nächste Umgebung des Sonnensystems und nicht für Sternentfernungen. Deshalb verwenden Astronomen stattdessen die zwei Einheiten Parsec (abgekürzt
für Parallaxensekunde oder parallaktische Sekunde, Einheitenzeichen pc) und Lichtjahr
(Einheitenzeichen ly).
Ein Parsec ist die Entfernung, von der aus betrachtet eine AE unter einem Winkel von
einer Bogensekunde erscheint. Mit anderen Worten ist ein Parsec jene Distanz, bei der ein
Stern eine jährliche Parallaxe von 100 hat. Weil 100 =
1◦
602
=
2π
360
602
rad ≈ 206 264,8−1 rad, erfolgt
die Umrechnung folgendermaßen:
1 pc =
1 AE
sin 100
≈ 206 264,8 AE
Das Parsec hat den Vorteil, dass aus einer in Bogensekunden angegebenen Parallaxe sehr
einfach die Entfernung (d) errechnet werden kann:
d=
1 AE
sin π
≈
1 AE
π [rad]
=
1 pc
π [00 ]
Ein Lichtjahr ist die Strecke, die eine elektromagnetische Welle wie das Licht in einem
Jahr im Vakuum zurücklegt. Das sind etwa 63 240 AE bzw. 0,3066 pc.
Abschließend seien die wichtigsten historischen Entwicklungen von Sternentfernungen
in Tabelle 3.1 und die aktuellen Distanzen zu den 20 nächsten Sternen bzw. Sternsystemen
und einigen „prominenten“ Gestirnen in Tabelle 3.224 25 zusammengefasst.
Tab. 3.1.: Historische Entwicklung der Einschätzung von Sternentfernungen
Zeit
der Publ.
um 150
um 1620
1728
172826
Person
Methode
Objekt
Ptolemäus
Kepler
Bradley
Newton
Sphärenmodell
u. a. Numerologie
abs. Parallaxe
Helligkeit
1838
1839
1840
Bessel
Henderson
Struve
rel. Parallaxe
abs. Parallaxe
rel. Parallaxe
Fixsternsphäre
Fixsternsphäre
γ Draconis
sonnenähnliche Sterne
erster Größenklasse
61 Cygni
α Centauri
Wega (α Lyrae)
Parallaxe
(0)
< 10
< 100
0,2200
Entfernung
[AE]
16,5
17 000
>400 000
950 000
0,313600 ± 0,020200
1,1600 ± 0,1100
0,261300 ± 0,025400
657 700
177 800
789 400
Vgl. RECONS: List of the Nearest 100 Stellar Systems. www.recons.org – Zugriff am 27.09.2008.
Vgl. CDS: SIMBAD database.
26
posthum erschienen
24
25
94
3.4. HEUTE
Dritte Sprosse: Nahe Sterne
Tab. 3.2.: Aktuelle Daten der 20 erdnächsten und einiger prominenter Sterne
#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
..
.
25
?
?
?
?
?
?
Bezeichnung
Eigenbewegung
[00 /a ]
Sonne
Proxima Centauri
α Centauri A
α Centauri B
Barnards Pfeilstern
Wolf 359
Lalande 21185
Sirius A
Sirius B
Luyten 726-8 A
Luyten 726-8 B
Ross 154
Ross 248
ε Eridani
Lacaille 9352
Ross 128
EZ Aquarii A
EZ Aquarii B
EZ Aquarii C
Procyon A
Procyon B
61 Cygni A
61 Cygni B
Struve 2398 A
Struve 2398 B
Groombridge 34 A
Groombridge 34 B
ε Indi A
ε Indi Ba
ε Indi Bb
DX Cancri
τ Ceti
Magnitude
[mag]
−26,72
11,09
0,01
1,34
9,53
13,44
7,47
−1,43
8,44
12,54
12,99
10,43
12,29
3,73
7,34
11,13
13,33
13,27
14,03
0,38
10,70
5,21
6,03
8,90
9,69
8,08
11,06
4,69
> 23
> 23
14,78
3,49
Parallaxe
3,853
3,710
3,724
10,358
4,696
4,802
1,339
1,339
3,368
3,368
0,666
1,617
0,977
6,896
1,361
3,254
3,254
3,254
1,259
1,259
5,281
5,281
2,238
2,238
2,918
2,918
4,704
4,823
4,823
1,290
1,922
0,76887 ± 0,00029
0,74723 ± 0,00117
0,74723 ± 0,00117
0,54698 ± 0,00100
0,41910 ± 0,00210
0,39342 ± 0,00070
0,38002 ± 0,00128
0,38002 ± 0,00128
0,37370 ± 0,00270
0,37370 ± 0,00270
0,33690 ± 0,00178
0,31600 ± 0,00110
0,30999 ± 0,00079
0,30364 ± 0,00087
0,29872 ± 0,00135
0,28950 ± 0,00440
0,28950 ± 0,00440
0,28950 ± 0,00440
0,28605 ± 0,00081
0,28605 ± 0,00081
0,28604 ± 0,00056
0,28604 ± 0,00056
0,28300 ± 0,00169
0,28300 ± 0,00169
0,28059 ± 0,00095
0,28059 ± 0,00095
0,27584 ± 0,00069
0,27584 ± 0,00069
0,27584 ± 0,00069
0,27580 ± 0,00300
0,27439 ± 0,00076
Kapteyns Stern
Wega
Arcturus
Aldebaran
Canopus
Betelgeuse
Polaris (Nordstern)
8,84
0,03
−0,04
0,85
−0,72
0,58
2,01
8,670
0,351
2,279
0,199
0,031
0,029
0,046
0,25527 ± 0,00086
0,12893 ± 0,00055
0,08885 ± 0,00074
0,05009 ± 0,00095
0,01043 ± 0,00053
0,00763 ± 0,00164
0,00756 ± 0,00048
[00 ]
95
Entfernung
[pc]
1,30
1,34
1,34
1,83
2,39
2,54
2,63
2,63
2,68
2,68
2,97
3,16
3,23
3,29
3,35
3,45
3,45
3,45
3,50
3,50
3,50
3,50
3,53
3,53
3,56
3,56
3,63
3,63
3,63
3,63
3,64
[103 AE]
0,001
268,3
276,0
276,0
377,1
492,2
524,3
542,8
542,8
552,0
552,0
612,2
652,7
665,4
679,3
690,5
712,5
712,5
712,5
721,1
721,1
721,1
721,1
728,9
728,9
735,1
735,1
747,8
747,8
747,8
747,9
751,7
[ly]
4,24
4,36
4,36
5,96
7,78
8,29
8,58
8,58
8,73
8,73
9,68
10,32
10,52
10,74
10,92
11,27
11,27
11,27
11,40
11,40
11,40
11,40
11,52
11,52
11,62
11,62
11,82
11,82
11,82
11,83
11,89
3,92
7,76
11,25
19,96
ca. 96
ca. 131
ca. 132
808,0
1 599,8
2 321,5
4 117,9
ca. 19 800
ca. 27 000
ca. 27 300
12,78
25,30
36,71
65,11
ca. 312
ca. 427
ca. 431
A. Didaktische Aspekte
A.1. Legitimation von astronomischen
Entfernungsbestimmungen
Obwohl die konkrete Sinnhaftigkeit von makroskopischen Entfernungsbestimmungen für
die Gesellschaft auf den ersten Blick in Frage gestellt werden kann, spielen diese seit jeher
eine zentrale Rolle in der Astronomie. Während man der Messung des Erdradius bzw.
-umfangs noch einen konkreten Nutzen zusprechen kann, haben die genauen Abstände
zum Mond, den Planeten oder den Sternen wohl kaum einen direkten Einfluss auf die
Menschheit, außer auf die wenigen Astronauten. Dennoch wird auch im Oberstufen–
Lehrplan für das Pflichtfach Physik an allgemeinbildenden höheren Schulen (AHS) diesem
Thema ein hoher Stellenwert gewidmet. So scheint als eines von sechs Bildungszielen in
der 5. und 6. Klasse folgender Punkt auf: „Größenordnungen im Mikro- und Makrokosmos
kennen und unsere Stellung im Universum einschätzen können.“
Auf die Fragen, was die vielen in dieser Arbeit genannten Gelehrten dazu bewegte, so
viel Zeit in die Bestimmung unüberwindbarer und großteils unvorstellbarer Entfernungen
zu investieren, und warum auch Schülerinnen und Schüler1 sich damit befassen sollten,
gelten ähnliche Antworten. Es geht um die Befriedigung von Neugier, Schaffung von Kultur
im weitesten Sinn und eine Art Daseinsdeutung des Menschen.
Die Astronomie (und damit auch die Entfernungsbestimmung) erlangte nebenbei auch
eine Legitimation als Grundlagenwissenschaft, im Zuge derer auch viele beiläufige und oft
unerwartete Erfolge gefeiert wurden.
Um nicht einem Streit über Inhalte von Allgemeinbildung oder den Selbstzweck von
Bildung zu verfallen, können für die Behandlung des Themas in der Schule, wie für den
Physikunterricht im Allgemeinen, noch andere Argumente gebracht werden. Einerseits
werden Fähigkeiten wie Objektivität und nachvollziehbares, logisches Denken gefördert,
andererseits lernt man, einen Sachverhalt genau zu beobachten, ihn auf das Wesentliche
zu reduzieren und anschließend zu modellieren.
1
Aus Gründen der leichteren Lesbarkeit wird fortan auf eine geschlechtsspezifische Differenzierung
verzichtet. Entsprechende Begriffe gelten im Sinne der Gleichbehandlung für beide Geschlechter.
96
A.2. GENETISCHER UNTERRICHT
Didaktische Aspekte
Außerdem kann anhand der einzelnen Sprossen der Entfernungsleiter und den damit
eng verbundenen Fragen zur Erdgestalt und dem Weltbild ein Einblick in den langen
Entstehungsprozess von Erkenntnissen gegeben werden.
Es sei noch darauf hingewiesen, dass bei Schülerumfragen über das Interesse im Physikunterricht astronomische Themen am besten abschneiden, weshalb sich die Frage nach der
Legitimation im Gegensatz zu anderen physikalischen Inhalten selten stellt.
A.2. Genetischer Unterricht
Aus oben genannten Gründen eignet sich das Themengebiet vorzüglich für einen genetischen2 Unterrichtstil. Dabei handelt es sich um ein Konzept, das auf den anerkannten
deutschen Mathematik- und Physikdidaktiker Martin Wagenschein (1896–1988) zurückgeht.
Er beschreibt „genetisch“ genauer als „genetisch – sokratisch – exemplarisch“.
„Genetisch“ bezieht sich dabei einerseits auf meist sehr langwierige historische Entwicklungen wissenschaftlicher Theorien bis hin zur heutigen Erkenntnis, andererseits auf die
Erkenntnisentwicklung des Schülers. Dabei wird besonderer Wert auf die Anknüpfung
an das Vorwissen und die Vorstellungen der Schüler gelegt. Zu beachten ist, dass der
Weg des Unterrichts nicht der Wissenschaftsgeschichte verpflichtet ist, sondern didaktisch
fruchtbare Situationen sucht.
„Sokratisch“ bedeutet, dass das Gespräch als Mittel zum Erkenntnisgewinn dient. „Wie
Sokrates in seinen berühmten Dialogen, so soll auch der Lehrer das Gespräch mit den
Schülern führen: nicht dozierend, dogmatisch, sondern als einen Dialog mit Zeit zum
Nachdenken, ein Herantasten an die Begriffe. Die Initiative muss beim Schüler bleiben,
um zu vermeiden, dass dieser nur leere Worthülsen von sich gibt, ohne deren Inhalt
wirklich zu verstehen. Wichtig ist nicht ein bestimmter Begriff, sondern der Weg, der zur
Begriffsbildung führt.“3
Ein „exemplarischer“ Unterricht bietet einen Ausweg aus der Stofffülle der Physik an.
Wagenschein charakterisiert dieses Prinzip durch „Mut zur Lücke“. Anhand stellvertretender Themen, die dafür umso genauer behandelt werden, sollen physikalische Denkweisen
und wissenschaftliches Arbeiten vermittelt werden. So wird vermieden, dass Schüler zwar
viel Faktenwissen erwerben, das tiefere Verständnis jedoch auf der Strecke bleibt. Beson2
3
gr. γ
´ νσις (génesis) „Entstehung“
KIRCHER, Ernst/GIRWIDZ, Raimund/HÄUSSLER, Peter: Physikdidaktik – Eine Einführung. Springer, 2001,
S. 196.
97
A.3. EINSTIEGE UND METHODEN
Didaktische Aspekte
deres Augenmerk muss darauf gelegt werden, dass trotz des auf Beispiele konzentrierten
Vorgehens Zusammenhänge zwischen den Themengebieten begreifbar werden.
A.3. Einstiege und Methoden
Einen wichtigen Teil stellt auch im genetischen Unterricht der Einstieg in ein neues Thema
dar. Es bietet sich an, auf Alltagsphänomene oder Schülervorstellungen einzugehen, um
die Schüler zu motivieren. „Diese Vorstellungen werden weiterentwickelt und geändert,
ohne jedoch zu schnell eine, dem Lernenden noch fremde Methode der Wissensaneignung
vorzuschlagen oder anzuordnen (die naturwissenschaftlichen Methoden), unverstandenes
Wissen (z. B. physikalische Begriffe) überzustülpen, in verfrühte Fachterminologien zu
verfallen.“4
Im konkreten Fall der Entfernungsleitersprossen kann es sich beispielsweise um eine der
folgende Einstiegsfragen handeln, wobei die Entfernungsleiter selbst einen zusätzlichen
sinnstiftenden Kontext bildet:
• Kann man mit einem Auge noch Entfernungen abschätzen?
Oft wird in der Schule bezüglich der Raumwahrnehmung nur kurz auf stereoskopisches Sehen im Biologieunterricht als Unterschied zwischen Raub- und Fluchttieren
eingegangen. Dass binokulare Raumwahrnehmung nur eine von vielen ist, wird
jedoch selten gelehrt.
• Wie kam man darauf, dass die Erde eine Kugel ist?
Die Kugelgestalt der Erde ist schon Volksschülern ein Begriff. Jedoch können die
meisten als Argumente für diese Tatsache nur Fotos von unserem Planeten, die im
All aufgenommen wurden, vorbringen.
• Wie kommen die Mondphasen zustande?
Ein weit verbreiteter Glaube ist, dass die Mondphasen mit dem Erdschatten zusammenhängen, obwohl diese Theorie bei einem Blick auf den Mond, wenn er gleichzeitig
mit der Sonne am Himmel steht, sofort unhaltbar wird.
• Wieso sollte sich die Erde um die Sonne drehen und nicht umgekehrt?
Obwohl auch diese Tatsache meist schon in der Volksschule bekannt ist, können dafür
die wenigsten Begründungen anführen – und schon gar nicht Beweise.
4
KIRCHER/GIRWIDZ/HÄUSSLER: Physikdidaktik, S. 194.
98
A.3. EINSTIEGE UND METHODEN
Didaktische Aspekte
Abb. A.1.: Ein Foto dreier normalwüchsiger Männer in einem Ames-Raum als Beispiel für eine
optische Täuschung.
Im Idealfall können die Schüler anschließend in einem sokratischen Dialog und durch
Nachvollziehen der historischen Entwicklung zu einem „Aha-Erlebnis“ kommen und so
ihre alten Alltagsvorstellungen dauerhaft ändern.
Zusätzlich bieten sich eine Menge forschender bzw. entdeckender Methoden an:
Zum einführenden Thema „Raumwahrnehmung“ könnten Schüler die einzelnen Hinweise, die uns räumliches Sehen ermöglichen, selbst erproben und nach ihrer Wichtigkeit und
Reichweite reihen. Dabei sollte nicht auf optische Täuschungen wie die Mondtäuschung, die
falsche Mondneigung oder den so genannten Ames-Raum (s. Abb. A.1) verzichtet werden.
Um den Begriff der Parallaxe verständlich zu machen, könnte man den Daumensprung
genauer betrachten. Einleitend ließe sich Abbildung A.2 verwenden.
Die in dieser Arbeit erwähnten Messmethoden für den Erdradius, insbesondere die
von Eratosthenes, eignen sich alle zum Einsatz in der Schule. Wagenschein betont die
Bedeutung dieses Verfahrens als Einstieg für einen exemplarischen Mathematikunterricht5 .
Es kann nicht nur Themen wie Parallelwinkel, Ähnlichkeitssätze, Strahlensatz oder die
Winkelsumme im Dreieck einleiten und verbinden, sondern steht stellvertretend „für das
Verhältnis der Mathematik zur physischen Welt“6 und lässt erfahren, „wie Mathematik im
ursprünglichen Umgang mit der Welt im Menschen entsteht, aus ihm also und aus den
Dingen hervorgeht.“7
5
Vgl. WAGENSCHEIN, Martin: Ursprüngliches Verstehen und exaktes Denken. Klett, 1965, S. 430ff.
Vgl. ibid., S. 433.
7
Vgl. ibid., S. 430.
6
99
A.3. EINSTIEGE UND METHODEN
Didaktische Aspekte
Abb. A.2.: Der Daumensprung als einführendes Beispiel für Parallaxen.
Auch die Dichotomiemethode Aristarchs zur Bestimmung der Sonnenentfernung und
eine Abwandlung von Hipparchs erster Methode zur Bestimmung der Mondentfernung
wurden schon von Wagenschein zur Verwendung in der Schule vorgeschlagen8 . Genauer
gesagt wird der Wert der Mondparallaxe durch gleichzeitige Höhenmessungen an zwei
weit voneinander entfernten Orten gefunden. Wagenschein verwendet hier die historischen
Messungen der zwei französischen Astronomen Nicolas Louis de Lacaille (1713 – 1762) und
Jérôme Lalande (1732 – 1807). Ersterer maß für die Höhe des genau im Norden stehenden
Mondes am 23. Feber 1752 am Kap der Guten Hoffnung 34◦ 170 , letzterer für den in Berlin
im Süden stehenden Mond 57◦ 550 . Da die beiden Orte fast dieselbe geographische Länge
besitzen, sind nur die Breitgrade ausschlaggebend. Diese können die Schüler leicht im
Atlas oder Internet finden und kommen so mit bekanntem Erdradius auf ein vollständig
bestimmtes Viereck.
8
Vgl. WAGENSCHEIN: Natur physikalisch gesehen, S. 45f.
100
A.3. EINSTIEGE UND METHODEN
Didaktische Aspekte
Abb. A.3.: Mondfinsternis am 4. März 2007
Auf die tatsächlichen Größen von Sonne und Mond kann dann durch eigenhändige
Messung des Winkeldurchmessers von einem der beiden Gestirne geschlossen werden.
Dazu könnte man den Abstand messen, in dem beispielsweise eine Münze entweder im
Sonnenlicht keinen Kernschatten mehr wirft, oder den Mond gerade verdeckt.
Aber auch Hipparchs Methode mit dem Eklipsendiagramm eignet sich gut für den
Unterricht. Die Erdschattenbreite in Mondentfernung könnte dabei auch von Schülern aus
einem Bild einer Mondfinsternis wie Abbildung A.3 gewonnen werden, bei dem aus der
Krümmung der Schattengrenze auf dem Mond im Bezug zum Mondradius gestellt werden
kann9 .
Die Bestimmung der Sonnenentfernung mit Hilfe des Venustransits wurde anlässlich
des seltenen Ereignisses am 8. Juni 2004 in vereinfachter Form an zahlreichen Schulen
nachvollzogen. Hierzu finden sich viele Unterlagen, Erfahrungsberichte und sogar Simulationssoftware10 im Internet. Ein Nachvollziehen von Halleys oder der in dieser Arbeit
beschriebenen Methode erweist sich für den normalen Unterricht sicher als zu komplex.
Um die Abstände im Sonnensystem zu veranschaulichen, eignet sich ein so genannter
Planetenweg, also eine zu den Radien der Planetenbahnen maßstabsgetreue Strecke,
die mit den Schülern abgegangen wird. Dadurch festigen sich die Größenordnungen im
Gedächtnis der Schüler.
Für die Methoden von Eratosthenes und Lacaille/Lalande besteht auch die Möglichkeit
eines internationalen Projekts. Dabei vermessen Schüler weit voneinander entfernter
9
Vgl. REBLE, Martin: Die Bestimmung der Mondentfernung nach Hipparch. Astronomie und Raumfahrt, 41
2004, Nr. 4, S. 12f.
10
z. B. XEphem (s. „Der Venustransit am 8. Juni 2004“ auf lehrer-online.de) oder TransitLAB (s. Project
CLEA auf www3.gettysburg.edu/~marschal/clea/CLEAhome.html)
101
A.4. FÄCHERÜBERGREIFENDE INHALTE
Didaktische Aspekte
Schulen den Schatten eines Stabes in der Mittagssonne oder fotografieren den Mond mit
Sternen oder Planeten im Hintergrund als Referenz, um dann ihre eigenen Ergebnisse
präsentieren zu können.
Zu allen historischen Messungen kann man, wie in dieser Arbeit oft geschehen, Originaltexte verwenden. Diese vermitteln den Schülern einen Eindruck über damalige Denkweisen
und werden so Bestandteil des genetischen Unterrichts.
Bei allen drei Sprossen werden Schüler mit der Messunsicherheit konfrontiert, ob nun
bei den Originalergebnissen oder den selbst durchgeführten Messungen. Dadurch lernen
sie den Umgang mit der Absolutheit wissenschaftlicher Errungenschaften.
A.4. Fächerübergreifende Inhalte
Alle Teilgebiete eignen sich als mathematische Anwendungsbeispiele, insbesondere stellt
die geometrische Entfernungsmessung eine Legitimation für die Trigonometrie dar.
Eine Zusammenarbeit bezüglich Beobachtungen mit ausländischen Schulen und die
Übersetzung von Originaltexten legen einen fächerübergreifenden Unterricht mit Fremdsprachen nahe.
Die historischen Hintergründe, die beispielsweise den antiken Griechen den Zugang zur
Wissenschaft als Selbstzweck oder in der Neuzeit eine Entwicklung von einer von wenigen
Universalgelehrten getragenen zu einer von immer mehr Spezialisten betriebenen Wissenschaft erst ermöglichten, könnten im Geschichte- bzw. Sozialkundeunterricht behandelt
werden. Andere dafür geeignete Themen wären die Endeckungsreisen und Kolonialmächte
im Zusammenhang mit dem Venustransit.
Die Winzigkeit des Menschen im Vergleich zu astronomischen Größenordnungen oder
das Verhältnis zwischen Kirche und Wissenschaft wären zwei mögliche Zusammenhänge
zu den Fächern Philosophie und Religion.
A.5. Arbeitsblatt
Angefügt ist ein Arbeitsblatt11 zum Thema Erdkrümmung, das sich sowohl für den Physik-,
als auch für den Mathematikunterrricht eignet und an die Methode von Al Bı̄rūnı̄ erinnert
(vgl. Abschn. 1.2). Als Vorkenntnisse genügen der Satz des Pythagoras und das Lösen von
Wurzelgleichungen.
11
Als Vorlage diente: ORTNER, Dieter: Unsere Erde – Kugel oder Scheibe?
www.dieterortner.ch/Diverses/Erdkruemmung/Erdkruemmung_Urnersee.pdf – Zugriff am
15.10.2008.
102
A.5. ARBEITSBLATT
Didaktische Aspekte
Die Erdkrümmung
Anfangs zwei einfache Rechnungen:
Das Rollfeld des Innsbrucker Flughafens ist ungefähr 2 km lang. Angenommen,
die Erde wäre eine perfekte Kugel mit einem Radius von 6 370 km und du hättest
ein 2 000 m langes Seil, das so leicht ist, dass es im gespannten Zustand nicht
durchhängt, also „schnurgerade“ ist.
Wie hoch müsste das Seil an beiden Enden montiert sein, dass es nirgendwo den
Boden berührt? Anders gefragt: Wie viel Zentimeter müssten an beiden Enden
der Rollbahn aufgeschüttet werden, damit sie vollkommen eben ist? [7,8 cm]
Wie hoch müsste das Seil an einem Ende montiert sein, wenn es am anderen
direkt am Boden verankert wäre? Anders gefragt: Wie hoch müsstest du dein
Fernglas mindestens halten, um etwas in 2 km Entfernung am Boden liegendes
sehen zu können? [31,4 cm]
Nun zur eigentlichen Aufgabe:
Die Abbildungen auf der nächsten Seite zeigen den Waldstätterhof, ein Hotel
am Ufer des Urnersee in der Schweiz, von verschiedenen Standpunkten aus
fotografiert. Das oberste Bild wurde aus der Nähe aufgenommen, die unteren
zwei vom 12 km entfernten gegenüberliegenden Ufer, wobei beim mittleren Foto
die Kamera 50 m, beim untersten 1 m über Seeniveau positioniert war.
Schätze nun z. B. anhand der Bäume, der Uferböschung und der Fenster ab, wie
viel Meter bei der untersten Aufnahme „verdeckt“ sind. Berechne daraus den
Erdradius unter der Annahme, dass die Wasseroberfläche exakt der Oberfläche
der Erdkugel entspricht. [6 m → 6 051 km; 5,5 m → 6 434 km]
Alternative ohne Wurzelgleichung: Wie viel von dem Hotel sollte theoretisch nicht
mehr gesehen werden können unter der Annahme, dass die Erde wirklich eine
Kugel mit einem Radius von 6 370 km ist? [5,58 m]
103
A.5. ARBEITSBLATT
Didaktische Aspekte
Abb. A.4.: Seehotel Waldstätterhof
104
B. Originaltexte
B.1. Aristarch
aus: ARISTARCHUS: On the Sizes and Distances of the Sun and Moon.
gefunden bei: HEATH, Thomas: Aristarchus of Samos – The ancient Copernicus Sandpiper
Books, 1997, S. 352ff.
105
B.1. ARISTARCH
Originaltexte
106
B.2. HIPPARCH
Originaltexte
B.2. Hipparch
aus: PAPPUS: Commentary on Almagest V 114, Ed. Rome S. 67 Z. 21 – S. 68 Z. 22.
gefunden bei: TOOMER, G. J.: Hipparchus on the Distances of the Sun and Moon. Archive for
History of Exact Sciences, 14 1974, Nr. 2, S. 126f.
„So Hipparchus, being uncertain concerning the sun, not only how great a parallax it has,
but whether it has any parallax at all, assumed in the first book of ‚On Sizes and Distances‘
that the earth has the ratio of a point and center to the sun [i.e. the sun’s sphere]. And at
one time, using the eclipse he adduced, he assumed it had the least parallax, and at another
time a greater parallax. Hence the ratios of the moon’s distances came out different. For in
Book 1 of ‚On Sizes and Distances‘ he takes the following observation: an eclipse of the
sun, which in the Hellespontine region was an exact eclipse of the whole sun, such that no
part of it was visible, but at Alexandria by Egypt approximately four-fifths of the diameter
was eclipsed. By means of the above he shows in Book 1 that, in units of which the radius
of the earth is one, the least distance of the moon is 71, and the greatest 83. Hence the
mean is 77. Having shown the foregoing, at the end of the book he says: ‚In this work we
have carried our demonstrations up to this point. But do not suppose that the question of
the moon’s distance has been thoroughly examined yet. For there remains some matter
for investigation in this subject too, by means of which the moon’s distance will be shown
to be less than what we have just computed.‘ Thus Hipparchus himself also admits that
he cannot be altogether sure concerning the parallaxes. Then again he himself in Book 2
of ‚On Sizes and Distances‘ shows from many considerations that, in units of which the
radius of the earth is one, the least distance of the moon is 62, the mean 67 13 , and the sun’s
distance 490. It is clear that the greatest distance of the moon will be 72 23 .“
107
B.3. PTOLEMÄUS
Originaltexte
B.3. Ptolemäus
aus: PTOLEMY: Planetary Hypotheses I 2, Ed. Heiberg fol. 89b.
gefunden bei: GOLDSTEIN, Bernard R.: The Arabic Version of Ptolemy’s Planetary Hypotheses.
American Philosophical Society, 1967, S. 7.
„Since the least distance of the Sun is 1 160 earth radii, as we mentioned, there is a
discrepancy between the two distances which we cannot account for; but we were led
inescapably to the distances which we set down. So much for the two (planetary) spheres
which lie closer to the earth than the others. The remaining spheres cannot lie between the
spheres of the Moon and the Sun, for even the sphere of Mars, which is the nearest to the
earth of the remaining spheres, and whose ratio of greatest to least distance is about 7:1,
cannot be accommodated between the greatest distance of Venus and the least distance of
the Sun. On the other hand it so happens that when we increase the distance to the Moon,
we are forced to decrease the distance to the Sun, and vice versa. Thus, if we increase the
distance to the Moon slightly, the distance to the Sun3 will be somewhat diminished and it
will then correspond to the greatest distance of Venus.“
108
B.4. NEWTON
Originaltexte
B.4. Newton
aus: NEWTON, I.: The System of the World
gefunden bei: Newton’s Principia: The Mathematical Principles of Natural Philosophy. To
which is added Newton’s System of the World. Übersetzt von A. MOTTE, veröffentlicht von D.
ADEE, First American edition, 1848, S. 547.
„...the disk of Saturn, which is only 1700 or 1800 in diameter, receives but about
1
2 100 000 000
of the sun’s light; for so much less is that disk than the whole spherical surface of the orb of
Saturn. Now if we suppose Saturn to reflect about
from its illuminated hemisphere will be about
1
4
of this light, the whole light reflected
1
4 200 000 000
of the whole light emitted from
the sun’s hemisphere; and, therefore, since light is rarefied in the duplicate ratio of the
p
distance from the luminous body, if the sun was 10 000 · 42 times more distant than
Saturn, it would yet appear as lucid as Saturn now does without its ring, that is, something
more lucid than a fixed star of the first magnitude. Let us, therefore, suppose that the
distance from which the sun would shine as a fixed star exceeds that of Saturn by about
100 000 times, and its apparent diameter will be 7v 16vi and its parallax arising from the
annual motion of the earth 130000 : and so great will be the distance, the apparent diameter,
and the parallax of the fixed stars of the first magnitude, in bulk and light equal to our
sun.“
109
Abbildungsverzeichnis
0.1. Raumwahrnehmung
(upload.wikimedia.org/wikipedia/commons/8/82/Mountainsrp.jpg) . . . . . . .
1
0.2. Bewegungsparallaxe
(www.kyb.mpg.de/bs/people/felix/UniPsy_VL_Wahrnehmung_WS05-06_Folien/
10-3D-Wahrnehmung.pdf) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
0.3. Horizont . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
0.4. Schatten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
0.5. Vermessung der Strecke Dünkirchen – Barcelona
(Alder, Ken: Das Maß der Welt. C. Bertelsmann, 2003, S. 13) . . . . . . . . . . . . . . . . . .
6
0.6. Pyramidenhöhe
(nach Webb, Stephen: Measuring the Universe. Springer, 1999, S. 16) . . . . . . . . . . . .
8
1.1. Hauptmeridian der hellenistischen Geographie
(Bialas, Volker: Erdgestalt, Kosmologie und Weltanschauung. Konrad Wittwer, 1982, S. 28) . 12
1.2. Skaphe
(www.martin-wagenschein.de/K-Kohl/Skaphe.jpg) . . . . . . . . . . . . . . . . . .
15
1.3. Erdumfang nach Eratosthenes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
15
1.4. Erdumfang nach Poseidonius . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
18
1.5. Arabische Meridiangradmessung im 8. Jh.
(Bachmann, Emil: Wer hat Himmel und Erde gemessen? Ott,1965, S. 54) . . . . . . . . . . . 19
1.6. Bestimmung des Erdradius nach Al Bı̄rūnı̄
(nach Bialas, Volker: Erdgestalt, Kosmologie und Weltanschauung. Konrad Wittwer, 1982, S. 64) 20
2.1. Winkel zwischen Sonne und Halbmond . . . . . . . . . . . . . . . . . . . . . . . . . . .
28
2.2. Strahlensatz 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
30
2.3. Durchmesser des Erdschattens . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
2.4. Strahlensatz 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
2.5. Sonnenparallaxe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
35
2.6. Mondparallaxe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
36
2.7. Hipparch 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
36
2.8. Hipparch 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
110
2.9. Epizykeltheorie 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
43
2.10.Epizykeltheorie 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
2.11.Planetenbahnen nach Ptolemäus
(nach people.scs.fsu.edu/~dduke/ptolemy.html) . . . . . . . . . . . . . . . . . . . . 47
2.12.Rückläufige Planetenbewegung nach Kopernikus
(en.wikipedia.org/wiki/Image:Retrograde_Motion.bjb.svg) . . . . . . . . . . . 52
2.13.Planetenentfernungen nach Kopernikus 1 . . . . . . . . . . . . . . . . . . . . . . . . . .
53
2.14.Planetenentfernungen nach Kopernikus 2 . . . . . . . . . . . . . . . . . . . . . . . . . .
53
2.15.Messung der maximalen Elongationen . . . . . . . . . . . . . . . . . . . . . . . . . . . .
55
2.16.Planetenbahnen nach Kopernikus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
2.17.Sternparallaxe (Fixsternsphäre) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
58
2.18.Tägliche Parallaxe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
2.19.Ellipsenbahn durch Epizykel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
2.20.Keplers Modell vom Sonnensystem
(Kepler, Johannes; Caspar, Max (Hrsg.): Mysterium Cosmographicum. Beck, 1943, Gesammelte Werke, Band 1, S. 26f) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
2.21.Planetenbahnen nach Kepler . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
63
2.22.Sonnenparallaxe nach Cassini . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
2.23.Venustransit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
2.24.Koordinatentransformation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
73
2.25.Venusspur . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74
2.26.Bewegung der Venus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
75
3.1. Sternparallaxe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
3.2. Relative Sternparallaxe
(de.wikipedia.org/wiki/Bild:ParallaxeV2.png) . . . . . . . . . . . . . . . . . . .
85
A.1. Ames-Raum
(cogsci.bme.hu/~ikovacs/latas2005/prepII_4_files/h_fig4.jpg) . . . . . . . 99
A.2. Daumensprung
(Verpackung einer Suchard JUNIOR Schokolade) . . . . . . . . . . . . . . . . . . . . . . . . 100
A.3. Mondfinsternis
(www.martin-wagner.org/mondfinsternis_august_2008.htm) . . . . . . . . . . . . 101
A.4. Waldstätterhof
(www.pictures-switzerland.com/brunnen/brunnen-hotel_small.JPG &
www.dieterortner.ch/Diverses/Erdkruemmung/Erdkruemmung_Urnersee.pdf) . 104
111
Tabellenverzeichnis
1.1. Historische Entwicklung der Einschätzung des Erdumfangs bis Picard . . . . . . . . . . 21
2.1. Aristarchs Ergebnisse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
2.2. Ptolemäus’ Ergebnisse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
48
2.3. Kopernikus’ Ergebnisse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
56
2.4. Keplers Ergebnisse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
63
2.5. Shorts Ergebnisse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
2.6. Historische Entwicklung der Einschätzung der Astronomischen Einheit . . . . . . . .
83
3.1. Historische Entwicklung der Einschätzung von Sternentfernungen . . . . . . . . . . . . 94
3.2. Aktuelle Daten der 20 erdnächsten und einiger prominenter Sterne . . . . . . . . . .
112
95
Literaturverzeichnis
ALDER, Ken: Der Meter misst keinen Meter! NZZ Folio, Die Zeitschrift der Neuen Zürcher Zeitung –
Thema: Normen, 2005, Nr. 02, S. 22–25
ARCHIMEDES; Czwalina, Arthur (Hrsg.): Über schwimmende Körper und die Sandzahl. Akademische Verlagsgesellschaft Leipzig, 1925
ARISTOTELES; Prantl, Karl (Hrsg.): Opera „Werke“, Band 2, gr. ΠERI OΥRANOΥ (peri uranu)/lat.
DE CAELO „Über das Himmelsgewölbe“. Neudr. d. Ausgabe Leipzig 1857, Scientia Verlag
Wien, 1978
BACHMANN, Emil: Wer hat Himmel und Erde gemessen? Ott, 1965
BATTERMANN, Hans Felix Heinrich: Beiträge zur Bestimmung der Mondbewegung und der Sonnenparallaxe aus Beobachtungen von Sternbedeckungen am sechsfüßigen Merz’schen Fernrohr
der Berliner Sternwarte. Beobachtungs-Ergebnisse der Königlichen Sternwarte zu Berlin, 5
1891, S. 1 – 42
BESSEL, Friedrich Wilhelm: Bestimmung der Entfernung des 61sten Sterns des Schwans. Astronomische Nachrichten, 16 1839, Nr. 366, S. 65 – 96
BESSEL, Friedrich Wilhelm; Schumacher, H. C. (Hrsg.): Populäre Vorlesungen über wissenschaftliche Gegenstände. Perthes-Besser & Mauke, 1848
BIALAS, Volker: Erdgestalt, Kosmologie und Weltanschauung – Die Geschichte der Geodäsie als Teil
der Kulturgeschichte der Menschheit. Konrad Wittwer, 1982
BRADLEY, James: A Letter to Dr. Edmond Halley Astronom. Reg. &c. giving an Account of a new
discovered Motion of the Fix’d Stars. Philosophical Transactions of the Royal Society, 35
1727 – 1728, S. 637 – 661
BRADLEY, James: A Letter to the Right honourable George Earl of Macclesfield concerning an
apparent Motion observed in some of the fixed Stars. Philosophical Transactions of the Royal
Society, 45 1748, S. 1 – 43
BROWNE, L.W. B.: Halley’s Method for Calculating the Earth – Sun Distance. Archive for History of
Exact Sciences, 59 2005, S. 251 – 266
113
CDS: SIMBAD database. simbad.u-strasbg.fr – Zugriff am 27.09.2008
COPERNICUS, Nicolaus: De revolutionibus orbium coelestium. Johannes Petreius, 1543, Faksimile unter ads.harvard.edu/books/1543droc.book oder la.wikisource.org/wiki/
Liber:De_revolutionibus_orbium_coelestium
COPERNICUS, Nicolaus; Zekl, Hans Günter (Hrsg.): Das neue Weltbild. Meiner, 1990
COWELL, Philip Herbert: Moon, semi-diameter, parallactic inequality, and variation of the, from
Greenwich meridian observations. Monthly Notices of the Royal Astronomical Society, 64
1903, S. 85 – 98
DIJKSTERHUIS, E. J.: Die Mechanisierung des Weltbildes. Springer, 1956
DIXON, Laurence: On Epicycles and Ellipses. wwwdata.unibg.it/dati/bacheca/63/21692.
pdf – Zugriff am 1.10.2008
ENCKE, Johann Franz: Über den Venusdurchgang von 1769. Abhandlungen der Königlichen Akademie der Wissenschaften zu Berlin, Mathematische Klasse 1835 (publ. 1837), S. 295 – 309
ENGELS, Donald: The Length of Eratosthenes’ Stade. The American Journal of Philology, 106 1985,
Nr. 3, S. 298–311
FERGUSON, Kitty: Das Maß der Unendlichkeit – Auf der Suche nach den Grenzen des Universums.
Aus dem Englischen von Friedrich Griese. Econ, 2000
FERNIE, J. D.: The Historical Search for Stellar Parallax. Journal of the Royal Astronomical Society
of Canada, 69 1975, Nr. 4, S. 153 – 161
GILL, David: Determination of the Solar Parallax, &c. vol. I., part 6. Combination of Results and
General Conclusions. Annals of the Cape Observatory, 6 1897, S. 5.1 – 5.32
GOLDSTEIN, E. Bruce: Wahrnehmungspsychologie. Spektrum, 2002
GREGORY, James: Optica Promota. excudebat J. Hayes, pro S. Thomson, ad insigne Episcopi,
1663, Übersetzung mit Kommentaren von Ian Bruce unter www.17centurymaths.com/
contents/contentsGregory.htm
HAEDER, Walter: Von der Königlichen Elle zum Meter. Beuth, 1973
HALL, A. Rupert: Newton on the calculation of central forces. Annals of Science, 13 1957, S. 62 – 71
HALLEY, Edmond: Methodus singularis qua Solis parallaxis sive distantia a Terra, ope Veneris
intra Solem conspiciendoe, tuto determinari poterit. Philosophical Transactions of the Royal
Society, 29 1714 – 1716, S. 454 – 464
114
HALLEY, Edmond: Considerations on the Change of the Latitudes of Some of the Principal Fixt Stars.
Philosophical Transactions of the Royal Society, 30 1717 – 1719, S. 736 – 738
HAUSTEIN, Heinz-Dieter: Weltchronik des Messens. de Gruyter, 2001
HEATH, Thomas: Aristarchus of Samos – The ancient Copernicus. Sandpiper Books, 1997
HELDEN, Albert Van: Measuring the Universe – Cosmic Dimensions from Aristarchus to Halley.
broschierte Auflage. Univ. of Chicago Press, 1986
HENDERSON, Thomas: On the Parallax of α Centauri. Monthly Notices of the Royal Astronomical
Society, 4 1839, Nr. 19, S. 168 – 169
HERRMANN, Dieter B.: Kosmische Weiten – Kurze Geschichte der Entfernungsmessung im Weltall.
3. Auflage. Deutsch, 1990
HERSCHEL, Friedrich Wilhelm: Catalogue of Double Stars. Philosophical Transactions of the Royal
Society, 72 1782, S. 112 – 162
HERSCHEL, Friedrich Wilhelm: On the Parallax of the Fixed Stars. Philosophical Transactions of the
Royal Society, 72 1782, S. 82 – 111
HINKS, Arthur Robert: Solar parallax papers. Monthly Notices of the Royal Astronomical Society,
70 1910, S. 588 – 603
HORNSBY, Thomas: The Quantity of the Sun’s Parallax, as Deduced from the Observations of the
Transit of Venus, on June 3, 1769. Philosophical Transactions of the Royal Society, 61 1771,
S. 574 – 579
HULTSCH, Friedrich: Poseidonios über die Größe und Entfernung der Sonne. Abhandlungen der
Königlichen Gesellschaft der Wissenschaften zu Göttingen, Philologisch-Historische Klasse,
Neue Folge 1 1897, Nr. 5
KEPLER, Johannes; Frisch, Christian (Hrsg.): Joannis Kepleri astronomi opera omnia 7. Band 7,
Heyder & Zimmer, 1868
KEPLER, Johannes; Caspar, Max (Hrsg.): Neue Astronomie. Oldenburg, 1929
KEPLER, Johannes; Caspar, Max (Hrsg.): Gesammelte Werke: Astronomia nova. Band 3, Beck,
1937
KEPLER, Johannes; Caspar, Max (Hrsg.): Gesammelte Werke: Epitome Astronomiae Copernicanae.
Band 7, Beck, 1953
KEPLER, Johannes; Caspar, Max (Hrsg.): Weltharmonik. Oldenburg, 1967
115
KIRCHER, Ernst/GIRWIDZ, Raimund/HÄUSSLER, Peter: Physikdidaktik – Eine Einführung. Springer,
2001
KLEOMEDES; Czwalina, Arthur (Hrsg.): Die Kreisbewegung der Gestirne. Akademische Verlagsgesellschaft Leipzig, 1927
KRÜGER, Reinhard: Eine Welt ohne Amerika. Weidler, 2000
KUHN, Thomas S.: The Copernican Revolution – Planetary Astronomy in the Development of
Western Thought. Harvard University Press, 1957
LE VERRIER, Urbain: Sur les masses des planètes et la parallaxe du Soleil. Comptes rendus hebdomadaires des séances de l’académie des sciences, 75 1872, S. 165 – 172
LOVELL, Barnard: Das unendliche Weltall – Geschichte der Kosmologie von der Antike bis zur
Gegenwart. dtv, 1988
MAYER, Christian: De novis in coelo sidereo phaenomenis in miris stellarum fixarum comitibus
Mannhemii. Typ. Elector Aulica & Academica, 1779
MICHELL, John: An Inquiry into the Probable Parallax, and Magnitude of the Fixed Stars, from the
Quantity of Light Which They Afford us, and the Particular Circumstances of Their Situation.
Philosophical Transactions of the Royal Society, 57 1767, S. 234 – 264
MILLER, Konrad: Die Erdmessung im Altertum und ihr Schicksal. Strecker und Schröder, 1919
NEUGEBAUER, Otto: A History of Ancient Mathematical Astronomy. Springer, 1975
NEWCOMB, Simon: Investigation of the Distance of the Sun and of the Elements which depend
upon it. Astronomical and Meteorological Observations made at the United States Naval
Observatory during the Year 1865, Appendix II. 1867, S. 1 – 29
NEWCOMB, Simon; Vogel, H. C. (Hrsg.): Popular Astronomy (dt.: Newcomb-Engelmanns populäre
Astronomie). 3. Auflage. Engelmann, 1905
NEWCOMB, Simon: Simon Newcombs Astronomie für jederman. 2. Auflage. Fischer, 1910
NEWTON, Isaac; Motte, Andrew (Hrsg.): Newton’s Principia: The Mathematical Principles of
Natural Philosophy. To which is added Newton’s System of the World. D. Adee, 1848
NEWTON, Isaac; Dellian, Ed (Hrsg.): Philosophiae Naturalis Principia Mathematica „Mathematische
Grundlagen der Naturphilosophie“. Meiner, 1988
NEWTON, Robert R.: The crime of Claudius Ptolemy. Johns Hopkins Univ. Press, 1977
116
ORTNER, Dieter: Unsere Erde – Kugel oder Scheibe? www.dieterortner.ch/Diverses/
Erdkruemmung/Erdkruemmung_Urnersee.pdf – Zugriff am 15.10.2008
PHYSIKALISCH-TECHNISCHE BUNDESANSTALT: Die PTB als Hüterin der Einheiten. www.ptb.de/de/
wegweiser/einheiten – Zugriff am 05.11.2007
PRAUSE, Wolfgang: Niemand hat Kolumbus ausgelacht – Fälschungen und Legenden der Geschichte
richtiggestellt. Econ, 1966
PTOLEMÄUS, Claudius; Manitius, Karl (Hrsg.): Handbuch der Astronomie. Band 1, Teubner, 1963,
Neuausgabe mit Vorwort und Berichtigungen von O. Neugebauer
PTOLEMÄUS, Claudius; Manitius, Karl (Hrsg.): Handbuch der Astronomie. Band 2, Teubner, 1963,
Neuausgabe mit Vorwort und Berichtigungen von O. Neugebauer
PTOLEMÄUS, Claudius; Goldstein, Bernard R. (Hrsg.): The Arabic Version of Ptolemy’s Planetary
Hypotheses. American Philosophical Society, 1967
RABE, Eugene: Additional note on the solar parallax from Eros. Astronomical Journal, 59 1954,
S. 409 – 411
REBLE, Martin: Die Bestimmung der Mondentfernung nach Hipparch. Astronomie und Raumfahrt,
41 2004, Nr. 4, S. 12f
RECONS: List of the Nearest 100 Stellar Systems. www.recons.org – Zugriff am 27.09.2008
ROTTLÄNDER, Rolf: Vormetrische Längenmaße. vormetrische-laengeneinheiten.de – Zugriff
am 24.10.2007
SHORT, James: The Observations of the Internal Contact of Venus with the Sun’s Limb, in the Late
Transit, Made in Different Places of Europe, Compared with the Time of the Same Contact
Observed at the Cape of Good Hope, and the Parallax of the Sun from Thence Determined.
Philosophical Transactions of the Royal Society, 52 1761 – 1762, S. 611 – 628
SHORT, James: Second Paper concerning the Parallax of the Sun Determined from the Observations
of the Late Transit of Venus, in Which This Subject is Treated of More at Length, and the
Quantity of the Parallax More Fully Ascertained. Philosophical Transactions of the Royal
Society, 53 1763, S. 300 – 345
SIMEK, Rudolf: Erde und Kosmos im Mittelalter – Das Weltbild vor Kolumbus. C. H. Beck, 1992
SPENCER JONES, Harold: Meeting of the Royal Astronomical Society. The Observatory, 64 1941,
Nr. 803, S. 99 – 104
117
STANDISH, E. Myles: The Astronomical Unit now. Proceedings of the International Astronomical
Union, 2004, Nr. 196, S. 163 – 179
STRUVE, Friedrich Georg Wilhelm: Über die Parallaxe des Sterns α Lyrae nach Micrometermessungen am großen Refractor der Dorpater Sternwarte. Astronomische Nachrichten, 17 1840,
Nr. 396, S. 177 – 180
STUMPFF, Karl: Die Erde als Planet. Springer, 1939
TEETS, Donald A.: Transits of Venus and the Astronomical Unit. Mathematics Magazine of the
Mathematical Association of America, 76 2003, Nr. 5, S. 335 – 148
TOOMER, G. J.: Hipparchus on the distances of the sun and moon. Archive for History of Exact
Sciences, 14 1974, Nr. 2, S. 126 – 142
TOOMER, G. J.: Hipparchus. In Gillispie, Charles Coulston (Hrsg.): Dictionary of scientific biography. Band 15, Scribner, 1981, S. 207 – 224
WAGENSCHEIN, Martin: Natur physikalisch gesehen. Diesterweg, 1960
WAGENSCHEIN, Martin: Ursprüngliches Verstehen und exaktes Denken. Klett, 1965
WEBB, Stephen: Measuring the Universe – The Cosmological Distance Ladder. Springer, 1999
ZINNER, Ernst: Astronomie – Geschichte ihrer Probleme. Band Orbis Academicus, II/1, Alber, 1951
118
Curriculum Vitae
Armin Lässer
Geboren am 21. Mai 1982 in Innsbruck
Wohnhaft in Innsbruck
AUSBILDUNG:
2002–2008
Lehramtsstudium Physik Mathematik an der LFU Innsbruck
2001–2002
2 Semester Studium der Telekommunikationstechnik und -systeme an
der FH Salzburg
1992–2000
Akademisches Gymnasium Innsbruck
119
Eidesstattliche Erklärung
Ich erkläre hiermit an Eides Statt, dass ich die vorliegende Diplomarbeit selbständig angefertigt habe. Ich habe dazu keine weiteren als die angeführten Hilfsmittel benutzt und die
aus anderen Quellen entnommenen Stellen als solche kenntlich gemacht. Insbesondere
wurden sämtliche Abbildungen, wenn nicht eigens im Abbildungsverzeichnis gekennzeichnet, von mir angefertigt.
Armin Lässer
120