Algorithmen und Datenstrukturen 1 - 5. Seminar

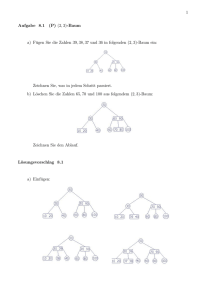
Algorithmen und Datenstrukturen 1
- 5. Seminar Dominic Rose
Bioinformatics Group, University of Leipzig
Wintersemester 2009/10
Outline
5.+6. Übungsserie: 5 Aufgaben, insgesamt 40 Punkte
A17 Baum-Traversierung (14 Punkte)
A18 AVL-Bäume(14 Punkte)
A19 Beweis (4 Punkte)
A20 Beweis (4 Punkte)
A21 Beweis (4 Punkte)
→ Zusammenfassung (Klausur)
Aufgabe 17
Ein Programm erzeugt eine Permutation einer einzugebenden Schlüsselfolge, indem es
die Schlüssel in der gegebenen Reihenfolge in einen anfangs leeren binären Suchbaum
einfügt und anschliessend in einem Durchlauf in Nebenreihenfolge (post-order
traversal) ausgibt.
Welche Ausgabe liefert das Programm bei Eingabe folgender Schlüsselsequenzen?
a) 1 2 3 4
b) 4 3 2 1
c) 3 2 1 4 5
d) 2 1 5 8 4 7 9
e) 6 2 7 3 1 4 5
f) 4 6 2 7 5 3 1
g) 1 2 3 4 5 6 7 9 8
→ 7x2 = 14 Punkte
Wiederholung: Traversieren von Bäumen
Verschiedene Möglichkeiten, die Knoten von Binärbäumen zu
durchlaufen. Man unterscheidet:
• pre-order Hauptreihenfolge: WLR
• in-order symmetrische Reihenfolge: LWR
• post-order Nebenreihenfolge: LRW
Allgemein: Traversieren von Graphen
• Baum: Zyklenfreier Graph
• Breitensuche (BFS - breadth-first-search)
• Tiefensuche (DFS - depth-first-search)
Allgemein: Traversieren von Graphen
• Breitensuche (BFS - breadth-first-search)
Durchlaufen der Knoten eines Graphen geordnet nach der
Entfernung von einem Startknoten. Zuerst werden alle
vom Startknoten direkt durch eine Kante erreichbaren
Knoten besucht, danach die mit zwei Kanten Entfernung,
dann die mit drei usw.
Allgemein: Traversieren von Graphen
• Tiefensuche (DFS - depth-first-search)
Vom Startknoten so weit wie möglich einen gewählten
Pfad entlang gehen. Am Ende eines Zweiges
angekommen, schrittweise zurück gehen, bis man
unbesuchten Teilbaum absteigen kann. Fertig, wenn man
wieder am Startknoten angelangt ist und es keine
unbesuchten direkten Nachbarknoten des Startknotens
mehr gibt. → Backtracking: Solange wie möglich gehen,
wenn man nicht mehr weiter kommt, zurückgehen bis
man einen anderen Weg findet.
Allgemein: Traversieren von Graphen
Aufgabe 17 (a)
post-order = Nebenreihenfolge = LRW
Eingabefolge: 1 2 3 4
Aufgabe 17 (b)
post-order = Nebenreihenfolge = LRW
Eingabefolge: 4 3 2 1
Aufgabe 17 (c)
post-order = Nebenreihenfolge = LRW
Eingabefolge: 3 2 1 4 5
Aufgabe 17 (d)
post-order = Nebenreihenfolge = LRW
Eingabefolge: 2 1 5 8 4 7 9
Aufgabe 17 (e)
post-order = Nebenreihenfolge = LRW
Eingabefolge: 6 2 7 3 1 4 5
Aufgabe 17 (f)
post-order = Nebenreihenfolge = LRW
Eingabefolge: 4 6 2 7 5 3 1
Aufgabe 17 (g)
post-order = Nebenreihenfolge = LRW
Eingabefolge: 1 2 3 4 5 6 7 9 8
Aufgabe 18
Konstruieren Sie zu jeder der in Aufgabe 17 angegebenen Schlüsselfolgen (a-g) einen
AVL-Baum, indem Sie die Schlüssel in der gegebenen Reihenfolge in einen anfangs
leeren AVL-Baum einfügen und nach jeder Einfügung die gegebenfalls notwendigen
Rotationen vornehmen. Zeichnen Sie für jede der Schlüsselfolgen (a-g) nur den
resultierenden Baum. Zwischenschritte brauchen nicht angegeben zu werden.
→ 7x2 = 14 Punkte
Wiederholung: l -balancierter Binärbaum
• Seien Bl (x) und Br (x) die linken und rechten TB eines
Knotens x und h(B) die Höhe eines Baumes B.
• Definition: Ein l-balancierter Binärbaum ist entweder leer
oder es ist ein Baum, bei dem für jeden Knoten x gilt:
|h(Bl (x)) − h(Br (x))| ≤ l .
• l läßt sich als Maß für die zulässige Entartung im
Vergleich zur ausgeglichenen Baumstruktur auffassen.
• 1-balancierter Binärbaum heißt AVL-Baum
Wiederholung: AVL-Baum
• Balancierungskriterium
|h(Bl (x)) − h(Br (x))| ≤ 1 .
• Der Balancierungsfaktor BF(x) eines Knotens x:
BF(x) = h(Bl (x)) − h(Br (x)) .
= Höhendifferenz der Unterbäume von x.
• Einfügen/Löschen von Knoten:
AVL-Kriterium darf nicht verletzt werden, sonst
Reorganisation: Einfach-/Doppelrotation.
Reorganisation: Rotation
4 Fälle:
1. Einfache Rechts-Rotation
2. Einfache Links-Rotation
3. Doppelte Rechts-/Links-Rotation
4. Doppelte Links-/Rechts-Rotation
Reorganisation: Einfachrotation
Einfache Rechts-Rotation:
Reorganisation: Einfachrotation
Einfache Links-Rotation:
Reorganisation: Einfachrotation
Einfachrotation im Allgemeinen:
Reorganisation: Doppelrotation
Doppelte Rechts-/Links-Rotation:
Reorganisation: Doppelrotation
Doppelte Links-/Rechts-Rotation:
AVL-Rebalancierung
Jeweils nach Einfügen oder Löschen eines Knotens i, für alle
Knoten y auf dem Pfad vom Vater von i bis zur Wurzel:
• Berechne BF(y ).
• Falls BF(y ) ≥ +2: Betrachte linken Tochterknoten x von
y . Bei BF(x) ≥ 0, rotiere rechts um y . Sonst
(BF(x) < 0), rotiere zuerst links um x, dann rechts um y .
• Falls BF(y ) ≤ −2: Betrachte rechten Tochterknoten x
von y . Bei BF(x) ≤ 0, rotiere links um y . Sonst
(BF(x) > 0), rotiere zuerst rechts um x, dann links um y .
Aufgabe 18 (a)
Eingabefolge: 1 2 3 4
Aufgabe 18 (a)
Eingabefolge: 1 2 3 4
Aufgabe 18 (b)
Eingabefolge: 4 3 2 1
Aufgabe 18 (b)
Eingabefolge: 4 3 2 1
Aufgabe 18 (c)
Eingabefolge: 3 2 1 4 5
Aufgabe 18 (c)
Eingabefolge: 3 2 1 4 5
Aufgabe 18 (d)
Eingabefolge: 2 1 5 8 4 7 9
Aufgabe 18 (d)
Eingabefolge: 2 1 5 8 4 7 9
Aufgabe 18 (e)
Eingabefolge: 6 2 7 3 1 4 5
Aufgabe 18 (e)
Eingabefolge: 6 2 7 3 1 4 5
Aufgabe 18 (f)
Eingabefolge: 4 6 2 7 5 3 1
Aufgabe 18 (f)
Eingabefolge: 4 6 2 7 5 3 1
Aufgabe 18 (g)
Eingabefolge: 1 2 3 4 5 6 7 9 8
Aufgabe 18 (g)
Eingabefolge: 1 2 3 4 5 6 7 9 8
Aufgabe 19
• Aufgabe: Sei T ein binärer Suchbaum mit paarweise
verschiedenen Schlüsseln. Der Schlüssel x befinde sich in
einem Knoten von T mit zwei nicht-leeren Unterbäumen.
Zeigen Sie: Der Nachfolger von x befindet sich in einem
Knoten mit leerem linken Unterbaum.
Aufgabe 19
• Aufgabe: Sei T ein binärer Suchbaum mit paarweise
verschiedenen Schlüsseln. Der Schlüssel x befinde sich in
einem Knoten von T mit zwei nicht-leeren Unterbäumen.
Zeigen Sie: Der Nachfolger von x befindet sich in einem
Knoten mit leerem linken Unterbaum.
• Lösungsidee: Beweis durch Widerspruch
Seien x, y Knoten im Baum T und y der Nachfolger von x
(y > x) und y habe einen nicht-leeren linken Teilbaum.
Wir zeigen, dass y nicht der Nachfolger von x in T sein
kann.
Aufgabe 19
Es gibt 3 Fälle für die rel. Anordnung von x und y im Baum T:
1.
2.
3.
Aufgabe 19
• Fall 1: x ist im linken Unterbaum des y -Knotens.
Der rechte Unterbaum des x-Knotens ist nicht-leer und
enthält einen Schlüssel z mit x < z < y . Damit ist y
nicht Nachfolger von x.
Aufgabe 19
• Fall 1: x ist im linken Unterbaum des y -Knotens.
Der rechte Unterbaum des x-Knotens ist nicht-leer und
enthält einen Schlüssel z mit x < z < y . Damit ist y
nicht Nachfolger von x.
• Fall 2: y ist im rechten Unterbaum des x-Knotens.
Der linke Unterbaum des y -Knotens ist nicht-leer und
enthält einen Schlüssel z mit x < z < y . Damit ist y
nicht Nachfolger von x.
Aufgabe 19
• Fall 1: x ist im linken Unterbaum des y -Knotens.
Der rechte Unterbaum des x-Knotens ist nicht-leer und
enthält einen Schlüssel z mit x < z < y . Damit ist y
nicht Nachfolger von x.
• Fall 2: y ist im rechten Unterbaum des x-Knotens.
Der linke Unterbaum des y -Knotens ist nicht-leer und
enthält einen Schlüssel z mit x < z < y . Damit ist y
nicht Nachfolger von x.
• Fall 3: Es gibt einen Knoten mit Schlüssel z, so dass sich
der x-Knoten im linken Unterbaum des z-Knotens und y
im rechten Unterbaum des z-Knotens befindet. Dann ist
x < z < y und somit y nicht Nachfolger von x.
Aufgabe 20
Ein binärer Suchbaum T mit n Knoten wird in
Nebenreihenfolge durchlaufen (post-order traversal), was eine
Schlüsselfolge a1 , a2 , . . . , an erzeugt. Die Schlüssel werden
anschliessend in umgekehrter Reihenfolge an , an−1 , . . . , a1 in
einen anfangs leeren binären Suchbaum iterativ eingefügt.
Zeigen Sie, dass der so konstruierte binäre Suchbaum gleich
dem eingegebenen Baum T ist.
Aufgabe 20
Ein binärer Suchbaum T mit n Knoten wird in
Nebenreihenfolge durchlaufen (post-order traversal), was eine
Schlüsselfolge a1 , a2 , . . . , an erzeugt. Die Schlüssel werden
anschliessend in umgekehrter Reihenfolge an , an−1 , . . . , a1 in
einen anfangs leeren binären Suchbaum iterativ eingefügt.
Zeigen Sie, dass der so konstruierte binäre Suchbaum gleich
dem eingegebenen Baum T ist.
Induktion über |T | (Anzahl der Stufen von T).
Aufgabe 20
• B(a) sei der binäre Suchbaum nach Einfügen der
Schlüssel der Sequenz a in einen anfangs leeren Baum.
• P(T ) sei die Schlüsselsequenz aus der
Post-Order-Traversierung des binären Suchbaums T .
• R(a) sei die Sequenz a nach Umkehrung der Reihenfolge.
• Induktionsbehauptung: B ◦ R ◦ P ist die Identität, also
für jeden binären Suchbaum T gilt T = B(R(P(T ))).
Aufgabe 20
Beweis per Induktion über |T |:
• Induktionsvoraussetzung: Für |T | = 0 ist P(T ) die leere
Sequenz, ebenso R(P(T )). Einfügen von nichts in den
leeren Suchbaum ergibt wieder den leeren Baum T .
Aufgabe 20
Beweis per Induktion über |T |:
• Induktionsvoraussetzung: Für |T | = 0 ist P(T ) die leere
Sequenz, ebenso R(P(T )). Einfügen von nichts in den
leeren Suchbaum ergibt wieder den leeren Baum T .
• Induktionsannahme: Sei |T | > 0 und für alle binären
Suchbäume U mit |U| < |T | gelte die Gleichung
U = B(R(P(U))).
• Den linken bzw. rechten Teilbaum von T nennen wir Tl
bzw. Tr , die Wurzel w , so dass T = (Tl , w , Tr ).
Aufgabe 20
Induktionsschluss:
• Dann ist P(T ) = P(Tl ) P(Tr ) w und somit
R(P(T )) = w R(P(Tr )) R(P(Tl )).
• Nach Induktionsannahme ist B(R(P(Tl ))) = Tl und
B(R(P(Tr ))) = Tr .
• Da alle Schlüssel aus der Sequenz R(P(Tr )) grösser als w
und alle Schlüssel aus der Sequenz R(P(Tl )) kleiner als w
sind, finden wir:
B(R(P(T ))) = B( w R(P(Tr )) R(P(Tl )) ) =
(B(R(P(Tl ))), B(w ), B(R(P(Tr ))) = (Tl , w , Tr ) = T .
Aufgabe 21
Seien T1 und T2 binäre Suchbäume, die dieselben Schlüssel
enthalten, jedoch verschiedene Struktur besitzen. Zeigen Sie,
dass sich T1 durch eine geeignete Folge von Rotationen in T2
überführen lässt.
Aufgabe 21
Vorbetrachtungen:
• Für einen Knoten v auf Stufe i > 0 in einem binären
Suchbaum T gibt es eine Rotation R, nach welcher sich
der Knoten v auf Stufe i − 1 befindet.
Aufgabe 21
Vorbetrachtungen:
• Für einen Knoten v auf Stufe i > 0 in einem binären
Suchbaum T gibt es eine Rotation R, nach welcher sich
der Knoten v auf Stufe i − 1 befindet.
• Bezeichne w den Vaterknoten von v . Je nachdem, ob v
linkes oder rechtes Kind von w ist, ist R als Rechts- bzw.
Links-Rotation um w zu wählen.
Aufgabe 21
Vorbetrachtungen:
• Für einen Knoten v auf Stufe i > 0 in einem binären
Suchbaum T gibt es eine Rotation R, nach welcher sich
der Knoten v auf Stufe i − 1 befindet.
• Bezeichne w den Vaterknoten von v . Je nachdem, ob v
linkes oder rechtes Kind von w ist, ist R als Rechts- bzw.
Links-Rotation um w zu wählen.
• Durch Induktion folgt, dass jeder Knoten, der sich
ursprünglich auf Stufe i befunden hat, durch eine Abfolge
von i Rotationen auf Stufe 0 gebracht werden kann, also
zur Wurzel des Baums gemacht werden kann.
Aufgabe 21
Beweis:
• Seien nun T1 und T2 wie in der Aufgabenstellung, wobei
x der Schlüssel in der Wurzel von T2 sei.
Aufgabe 21
Beweis:
• Seien nun T1 und T2 wie in der Aufgabenstellung, wobei
x der Schlüssel in der Wurzel von T2 sei.
• Gemäß Vorbetrachtung kann der Knoten v , der den
Schlüssel x im Baum T1 enthält, durch eine endliche
Abfolge von Rotationen zur Wurzel des Baum gemacht
werden.
Aufgabe 21
Beweis:
• Seien nun T1 und T2 wie in der Aufgabenstellung, wobei
x der Schlüssel in der Wurzel von T2 sei.
• Gemäß Vorbetrachtung kann der Knoten v , der den
Schlüssel x im Baum T1 enthält, durch eine endliche
Abfolge von Rotationen zur Wurzel des Baum gemacht
werden.
• Wenden wir diese Rotationsfolge auf T1 an und nennen
den resultierenden Baum T∗ .
Aufgabe 21
Beweis:
• Seien nun T1 und T2 wie in der Aufgabenstellung, wobei
x der Schlüssel in der Wurzel von T2 sei.
• Gemäß Vorbetrachtung kann der Knoten v , der den
Schlüssel x im Baum T1 enthält, durch eine endliche
Abfolge von Rotationen zur Wurzel des Baum gemacht
werden.
• Wenden wir diese Rotationsfolge auf T1 an und nennen
den resultierenden Baum T∗ .
• Die Wurzel von T∗ enthält den Schlüssel x.
Aufgabe 21
Beweis:
• Seien nun T1 und T2 wie in der Aufgabenstellung, wobei
x der Schlüssel in der Wurzel von T2 sei.
• Gemäß Vorbetrachtung kann der Knoten v , der den
Schlüssel x im Baum T1 enthält, durch eine endliche
Abfolge von Rotationen zur Wurzel des Baum gemacht
werden.
• Wenden wir diese Rotationsfolge auf T1 an und nennen
den resultierenden Baum T∗ .
• Die Wurzel von T∗ enthält den Schlüssel x.
• Dementsprechend enthält der linke Teilbaum von T∗
dieselben Schlüssel wie der linke Teilbaum von T2 ,
nämlich genau diejenigen, die kleiner als x sind.
Aufgabe 21
Beweis:
• Entsprechend enthalten die rechten Teilbäume von T∗
und T2 beide genau die Schlüssel größer als x.
Aufgabe 21
Beweis:
• Entsprechend enthalten die rechten Teilbäume von T∗
und T2 beide genau die Schlüssel größer als x.
• Daher können wir nun die Vorbetrachtung separat auf
den linken und den rechten Teilbaum anwenden und
anschliessend auf deren Teilbäume und so weiter.
Aufgabe 21
Beweis:
• Entsprechend enthalten die rechten Teilbäume von T∗
und T2 beide genau die Schlüssel größer als x.
• Daher können wir nun die Vorbetrachtung separat auf
den linken und den rechten Teilbaum anwenden und
anschliessend auf deren Teilbäume und so weiter.
• Nach der i-ten solchen Rekursion ist der resultierende
Baum auf den Stufen 0 bis i − 1 gleich dem Baum T2 .
Aufgabe 21
Beweis:
• Entsprechend enthalten die rechten Teilbäume von T∗
und T2 beide genau die Schlüssel größer als x.
• Daher können wir nun die Vorbetrachtung separat auf
den linken und den rechten Teilbaum anwenden und
anschliessend auf deren Teilbäume und so weiter.
• Nach der i-ten solchen Rekursion ist der resultierende
Baum auf den Stufen 0 bis i − 1 gleich dem Baum T2 .
• Daher sind maximal h(T2 ) Rekursionen nötig, um T2 aus
T1 durch Rotationen zu erzeugen.
Klausur
03.02.2010, 17:15 - 18:45 Uhr, HS 8+9
• Asymptotische Komplexität
• Master-Theorem
• Suchen
• Sortieren
• Bäume
• Hashing
Wiederholung
• Groß-Oh-Notation: bringt zum Ausdruck, dass eine
Funktion f (n) höchstens so schnell wächst wie eine
andere Funktion g (n).
• Definition: Funktion f (n) ist in der Menge O(g (n)),
wenn es ein c > 0 und ein n0 ∈ N gibt, so dass für alle
n ≥ n0 gilt: f (n) ≤ c · g (n)
• Groß-Omega-Notation: f (n) wächst mindestens so
schnell wie g (n).
Wiederholung