Abbildungseigenschaften

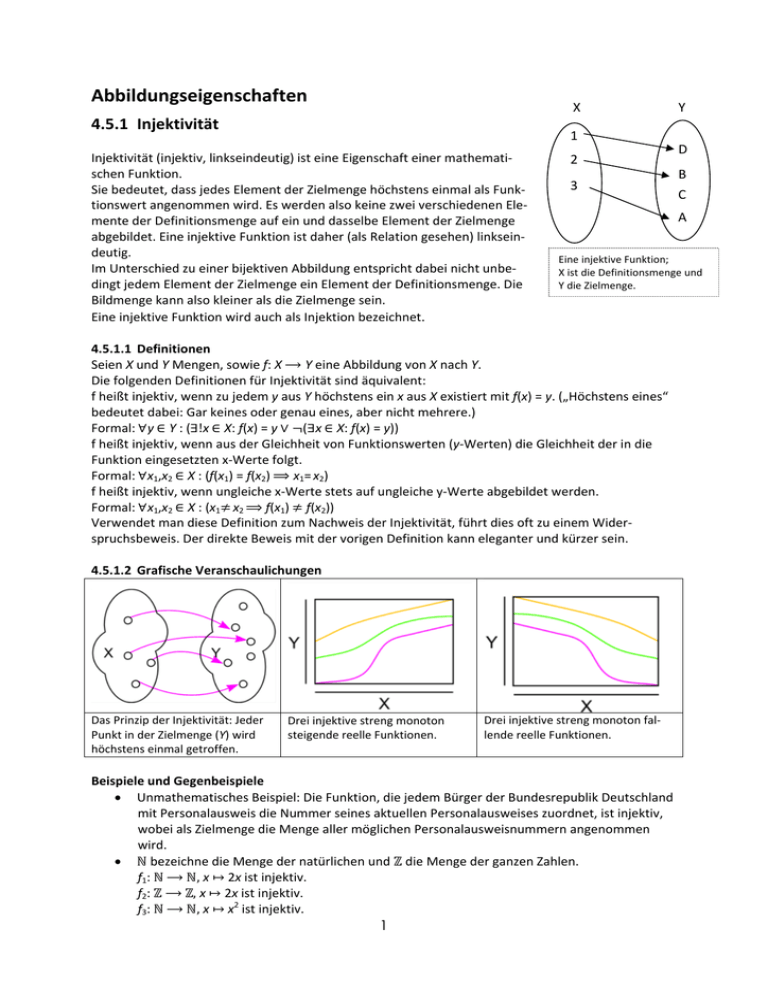
Abbildungseigenschaften X 4.5.1 Injektivität Y
1 D
Injektivität (injektiv, linkseindeutig) ist eine Eigenschaft einer mathemati‐
2 schen Funktion. B
3 Sie bedeutet, dass jedes Element der Zielmenge höchstens einmal als Funk‐
C
tionswert angenommen wird. Es werden also keine zwei verschiedenen Ele‐
A mente der Definitionsmenge auf ein und dasselbe Element der Zielmenge abgebildet. Eine injektive Funktion ist daher (als Relation gesehen) linksein‐
deutig. Eine injektive Funktion; Im Unterschied zu einer bijektiven Abbildung entspricht dabei nicht unbe‐
X ist die Definitionsmenge und dingt jedem Element der Zielmenge ein Element der Definitionsmenge. Die Y die Zielmenge.
Bildmenge kann also kleiner als die Zielmenge sein. Eine injektive Funktion wird auch als Injektion bezeichnet.
4.5.1.1 Definitionen Seien X und Y Mengen, sowie f: X ⟶ Y eine Abbildung von X nach Y. Die folgenden Definitionen für Injektivität sind äquivalent: f heißt injektiv, wenn zu jedem y aus Y höchstens ein x aus X existiert mit f(x) = y. („Höchstens eines“ bedeutet dabei: Gar keines oder genau eines, aber nicht mehrere.) Formal: ∀y ∈ Y : (∃!x ∈ X: f(x) = y ∨ (∃x ∈ X: f(x) = y)) f heißt injektiv, wenn aus der Gleichheit von Funktionswerten (y‐Werten) die Gleichheit der in die Funktion eingesetzten x‐Werte folgt. Formal: ∀x1,x2 ∈ X : (f(x1) = f(x2) ⟹ x1= x2) f heißt injektiv, wenn ungleiche x‐Werte stets auf ungleiche y‐Werte abgebildet werden. Formal: ∀x1,x2 ∈ X : (x1 x2 ⟹ f(x1) f(x2)) Verwendet man diese Definition zum Nachweis der Injektivität, führt dies oft zu einem Wider‐
spruchsbeweis. Der direkte Beweis mit der vorigen Definition kann eleganter und kürzer sein. 4.5.1.2 Grafische Veranschaulichungen Das Prinzip der Injektivität: Jeder Punkt in der Zielmenge (Y) wird höchstens einmal getroffen. Drei injektive streng monoton steigende reelle Funktionen. Drei injektive streng monoton fal‐
lende reelle Funktionen. Beispiele und Gegenbeispiele  Unmathematisches Beispiel: Die Funktion, die jedem Bürger der Bundesrepublik Deutschland mit Personalausweis die Nummer seines aktuellen Personalausweises zuordnet, ist injektiv, wobei als Zielmenge die Menge aller möglichen Personalausweisnummern angenommen wird. 
bezeichne die Menge der natürlichen und die Menge der ganzen Zahlen. f1: ⟶ , x ↦ 2x ist injektiv. f2: ⟶ , x ↦ 2x ist injektiv. f3: ⟶ , x ↦ x2 ist injektiv. 1
f4: ⟶ , x ↦ x2 ist nicht injektiv. 4.5.1.3 Eigenschaften  Eine stetige reellwertige Funktion auf einem reellen Intervall ist genau dann injektiv, wenn sie in ihrem gesamten Definitionsbereich streng monoton steigend oder streng monoton fal‐
lend ist, d.h. für zwei beliebige Zahlen a und b aus dem Definitionsbereich gilt: Aus a < b folgt f(a) < f(b) (steigend), bzw. aus a < b folgt f(a) > f(b) (fallend).  Man beachte, dass die Injektivität einer Funktion f: A ⟶ B nur vom Funktionsgraphen {(x,f(x))|x ∈ A} abhängt (im Gegensatz zur Surjektivität, die auch von der Zielmenge B ab‐
hängt, welche man am Funktionsgraphen nicht ablesen kann).  Sind die Funktionen f: A ⟶ B und g: B ⟶ C injektiv, dann gilt dies auch für die Komposition (Verkettung) g ∘ f : A ⟶ C .  Aus der Injektivität von g ∘ f folgt, dass f injektiv ist.  Eine Funktion f: A ⟶ B mit nichtleerer Definitionsmenge A ist genau dann injektiv, wenn f eine linke Inverse hat, also eine Funktion g: B ⟶ A mit g ∘ f = idA (wobei idA die identische Abbildung auf A bezeichnet).  Eine Funktion f: A ⟶ B ist genau dann injektiv, wenn f links kürzbar ist, also für beliebige Funktionen g, h: C ⟶ A mit f ∘ g = f ∘ h schon g = h folgt.  Eine Funktion f: A ⟶ B ist genau dann injektiv, wenn für alle Teilmengen X,Y ⊆ A gilt: f(X∩Y)= f(X)∩f(Y).  Jede beliebige Funktion f: A ⟶ B ist darstellbar als Verkettung f = h ∘ g, wobei g surjektiv und h injektiv (nämlich eine Inklusionsabbildung) ist. X Y 1 4.5.2 Surjektivität D
2
Surjektivität (surjektiv) ist eine Eigenschaft einer mathematischen B
3 Funktion. C
Sie bedeutet, dass jedes Element der Zielmenge mindestens einmal 4
als Funktionswert angenommen wird, also mindestens ein Urbild hat. In der Sprache der Relationen ist der entsprechende Begriff rechtsto‐
tal. Eine surjektive Funktion; Eine surjektive Funktion wird auch als Surjektion bezeichnet. X ist die Definitionsmenge und Y die Zielmenge.
4.5.2.1 Definition Es seien X und Y Mengen, sowie f: X ⟶ Y eine Abbildung. f heißt surjektiv, wenn für alle y aus Y mindestens ein x aus X mit f(x) = y existiert. Formal: ∀y ∈ Y ∃x ∈ X: f(x) = y 4.5.2.2 Grafische Veranschaulichungen Das Prinzip der Surjektivität: Jeder Drei surjektive Funktionen zwi‐
Punkt in der Zielmenge (Y) wird schen reellen Intervallen. mindestens einmal getroffen. 2
Ein Sonderfall der Surjektivität: Die Zielmenge (Y) besteht nur aus einem Element. 4.5.2.3 Beispiele und Gegenbeispiele  Die Funktion f: ⟶ mit f(x) = 2x + 1 ist surjektiv, denn für jede reelle Zahl y gibt es ein Ur‐
bild. Aus der Gleichung y = 2x + 1 erhält man nämlich durch Äquivalenzumformung die Glei‐
chung x = ½(y−1), womit sich für jedes y ein Urbild x berechnen lässt.  Die Sinus‐Funktion sin : ⟶ [‐1,1] ist surjektiv. Jede horizontale Gerade y = c mit ‐1 ≤ c ≤ 1 hat unendlich viele Schnittpunkte mit dem Graphen der Funktion.  Die Sinus‐Funktion sin : ⟶ ist jedoch nicht surjektiv, da z. B. die Gerade y = 2 keinen Schnittpunkt mit dem Graphen hat, der Wert 2 also nicht als Funktionswert angenommen wird. 
bezeichne die Menge der komplexen Zahlen. f1: ⟶ , x ↦ x2 ist nicht surjektiv. f2: ⟶ , x ↦ x2 ist surjektiv. 4.5.2.4 Eigenschaften  Man beachte, dass die Surjektivität einer Funktion f: A ⟶ B nicht nur vom Funktionsgraphen {(x,f(x))|x ∈ A}, sondern auch von der Zielmenge B abhängt (im Gegensatz zur Injektivität, welche man am Funktionsgraphen ablesen kann).  Sind die Funktionen f: A ⟶ B und g: B ⟶ C surjektiv, dann gilt dies auch für die Kompositi‐
on (Verkettung) g ∘ f : A ⟶ C .  Aus der Surjektivität von g ∘ f folgt, dass g surjektiv ist.  Eine Funktion f: A ⟶ B ist genau dann surjektiv, wenn f eine rechte Inverse hat, also eine Funktion g: B ⟶ A mit f ∘ g = idB (wobei idB die identische Abbildung auf B bezeichnet). Die‐
se Aussage ist äquivalent zum Auswahlaxiom der Mengenlehre.  Eine Funktion f: A ⟶ B ist genau dann surjektiv, wenn f rechts kürzbar ist, also für beliebige Funktionen g, h: B ⟶ C mit g ∘ f = h ∘ f schon g = h folgt.  Jede beliebige Funktion f: A ⟶ B ist darstellbar als Verkettung f = h ∘ g, wobei g surjektiv und h injektiv ist. g: A ⟶ im f hat dabei die Bildmenge von f als Zielmenge und stimmt an‐
sonsten mit f überein (hat denselben Funktionsgraphen). Y X 4.5.3 Bijektivität 1 D
Bijektivität (bijektiv oder umkehrbar eindeutig auf oder eineindeutig auf) ist 2 eine Eigenschaft einer mathematischen Funktion. B Eine Funktion ist bijektiv, wenn sie verschiedene Elemente ihres Definiti‐
3 C onsbereichs auf verschiedene Elemente der Zielmenge abbildet (sie also 4 injektiv ist), und wenn zusätzlich jedes Element der Zielmenge als Funkti‐
A onswert auftritt (sie also surjektiv ist). Eine bijektive Funktion hat daher immer eine Umkehrfunktion, ist also invertierbar. Eine bijektive Funktion; Eine bijektive Funktion nennt man auch eine Bijektion. Eine Bijektion einer X ist die Definitionsmenge und endlichen Menge auf sich selbst heißt auch Permutation. Y die Zielmenge.
Für endliche Mengen haben die Definitionsmenge, die Bildmenge und die Zielmenge einer Bijektion dieselbe Anzahl von Elementen. Umgekehrt ist eine Funktion zwischen endlichen Mengen bijektiv, wenn diese drei Zahlen übereinstimmen. Für unendliche Mengen definiert man die Mächtigkeit als Verallgemeinerung der Elementanzahl mit Hilfe des Begriffes der Bijektion.
4.5.3.1 Definition Sei f eine Funktion, die von X nach Y abbildet, also f: X ⟶ Y. f ist bijektiv, wenn für alle y ∈ Y genau ein x ∈ X mit f(x) = y existiert. Mit anderen Worten kann man dies so ausdrücken: f ist bijektiv, wenn f injektiv und surjektiv ist. 3
4.5.3.2 Grafische Veranschaulichungen Das Prinzip der Bijektivität: Jeder Punkt in der Zielmenge (Y) wird genau einmal getroffen. Vier bijektive streng monoton stei‐
gende reelle Funktionen. Vier bijektive streng monoton fal‐
lende reelle Funktionen. 4.5.3.3 Beispiele und Gegenbeispiele Die Menge der reellen Zahlen wird hier mit bezeichnet, die Menge der nichtnegativen reellen Zah‐
len mit 0+.  Die Funktion f: ⟶ , x ↦ x + a ist bijektiv mit der Umkehrfunktion f‐1: ⟶ , x ↦ x ‐ a.  Ebenso ist für a 0 die Funktion g: ⟶ , x ↦ ax bijektiv mit der Umkehrfunktion g‐1: ⟶ , x ↦ 

x
. a
Unmathematisches Beispiel: Ordnet man jedem (monogam) verheirateten Menschen seinen Ehepartner bzw. seine Ehepartnerin zu, ist dies eine Bijektion der Menge aller verheirateten Menschen auf sich selbst. Dies ist sogar ein Beispiel für eine selbstinverse Abbildung. Die folgenden vier Quadratfunktionen unterscheiden sich nur in ihren Definitions‐ bzw. Wer‐
temengen: f1: ⟶ , x ↦ x2 f2: 0+ ⟶ , x ↦ x2 f3: ⟶ 0+, x ↦ x2 f4: 0+ ⟶ 0+, x ↦ x2 Mit diesen Definitionen ist  f1 nicht injektiv, nicht surjektiv, nicht bijektiv  f2 injektiv, nicht surjektiv, nicht bijektiv  f3 nicht injektiv, surjektiv, nicht bijektiv  f4 injektiv, surjektiv, bijektiv 4.5.3.4 Eigenschaften  Sind A und B endliche Mengen mit gleich vielen Elementen und ist f: A ⟶ B eine Funktion, dann gilt: Ist f injektiv, dann ist f bereits bijektiv. Ist f surjektiv, dann ist f bereits bijektiv.  Insbesondere gilt also für Funktionen f: A ⟶ B von einer endlichen Menge A in sich selbst: f ist injektiv ⇔ f ist surjektiv ⇔ f ist bijektiv. Für unendliche Mengen ist das im Allgemeinen falsch. Diese können injektiv auf echte Teil‐
mengen abgebildet werden, ebenso gibt es surjektive Abbildungen einer unendlichen Menge auf sich selbst, die keine Bijektionen sind. Solche Überraschungen werden im Artikel Hilberts Hotel detaillierter beschrieben, siehe dazu auch Dedekind‐Unendlichkeit.  Sind die Funktionen f: A ⟶ B und g: B ⟶ C bijektiv, dann gilt dies auch für die Verkettung g ∘ f : A ⟶ C . Die Umkehrfunktion von g ∘ f ist dann f‐1 ∘ g‐1.  Ist g ∘ f bijektiv, dann ist f injektiv und g surjektiv. 4


Ist f : A ⟶ B eine Funktion und gibt es eine Funktion g: B ⟶ A, die die beiden Gleichungen g ∘ f = idA (idA = Identität auf der Menge A) f ∘ g = idB (idB = Identität auf der Menge B) erfüllt, dann ist f bijektiv, und g ist die Umkehrfunktion von f, also g = f−1. Die Bijektionen einer Menge A in sich selbst bilden, zusammen mit der Verkettung als Ver‐
knüpfung, eine Gruppe, die, falls A endlich ist, „symmetrische Gruppe“ heißt. 5