IR-Spektroskopie

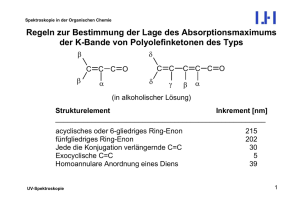
Spektroskopie in der Organischen Chemie
IR-Spektroskopie
-> A n r e g u n g
von
Molekülschwingungen bzw.
–rotationen
durch
Absorption von Strahlung
im infraroten (IR) Bereich
-> IR-Strahlung schliesst
sich dem sichtbaren
Bereich in Richtung
längerer Wellenlängen an
-> auch als Wärmestrahlung bekannt - erzeugt
Wärmengefühl auf der Haut
IR-Spektroskopie - 01
1
Spektroskopie in der Organischen Chemie
Messung von Molekülschwingungen und –rotation
 direkt als Absorption im IR-Spektrum
 indirekt als Streustrahlung im Raman-Spektrum
Lage der Absorptionsbande im IR-Spektrum:
 Einheiten der Wellenlänge λ des absorbierten Lichts, für
Strukturbestimmung organischer Moleküle interessant: λ = 2.5 –15 µm
 Gebräuchlicher: Angabe in Einheiten der reziproken Wellenlänge, der
sogenannten Wellenzahl ν~ - definiert als Frequenz/Lichtgeschwindigkeit:
ν~ = ν/c = 1/λ [cm-1]
Die Wellenzahl ist proportional ν und damit der aufenommenen Energie:
ΔE = hν = (hc)/λ = hc ν~
IR-Spektroskopie - 01
2
Spektroskopie in der Organischen Chemie
Infrarot-Spektralbereich (ca. 4000-400 cm-1)
Die große Bedeutung der IR-Spektroskopie ist die Tatsache, dass man auf den
ersten Blick das Vorhandensein oder die Abwesenheit bestimmter Absorptionsbanden funktioneller Gruppen, wie C=O, OH, C≡N u.v.a.m., erkennen
kann.
Valenzschwingungen ν
Deformationsschwi. δ
Fingerprint-Bereich: <1600 cm-1 -> sehr große Anzahl von Banden, deren
Ursprung oft nur sehr schwer zu identifizieren ist, die aber in ihrer Frequenzlage
IR-Spektroskopie - 01
3
Spektroskopie in der Organischen Chemie
und Intensität sehr charakteristisch für die Substanz selbst sind. Beim Vergleich
zweier IR-Spektren bedeutet ein praktisch gleicher Fingerprint-Bereich Identität
der verglichenen Substanzen.
Der Bereich der IR-Strahlung wird in drei Bereiche aufgeteilt: fernes, mittleres
und nahes IR, wobei sich die Angaben auf die Entfernung vom Bereich des
sichtbaren Lichtes beziehen. Das nahe IR-Licht hat also eine höhere Frequenz
(Energie) als das ferne.
1µ
m
10-4
10-1 cm
10.000
10 cm-1
Wellenzahl
ν~
1015
1011 Hz
Frequenz
ν
nahes
1 mm
mittleres
Wellenlänge λ
fernes
IR
Im nahen und mittleren IR-Bereich ( ν~= 10.000 - 200 cm-1) werden Molekül~
schwingungen angeregt, während im fernen IR ( ν = <200 cm-1) Rotationen und
Translationen angeregt werden. Hier kommt man dann schon in die Nähe des
Mikrowellen-Bereich.
IR-Spektroskopie - 01
4
Spektroskopie in der Organischen Chemie
Einfachstes Modell für Molekülschwingung: harmonischer Oszillator
Hooksches Gesetz: F = -kΔr
Rückstellkraft F proportional der Auslenkung Δr
k = Kraftkonstante – Mass für Bindungsstärke
Energie der Schwingung eines harmon. Osz.:
V(r) = 1/2kΔr2 = 2π2µνosc2Δr2
µ - reduzierte Masse (s. Anhang), νosc – Schwingungsfrequenz des Oszillators
νosc = 1/(2π) (k/µ)1/2
Zunahme von ν
 je grösser k -> kc≡c > kc=c > kc-c
 je kleiner die schwingenden Atommassen -> C-H <-> C-C
IR-Spektroskopie - 01
5
Spektroskopie in der Organischen Chemie
Aber: Dissoziation bei höherer Energie – besser beschreibbar mit
anharmonischem Oszillator
Und: Berücksichtigung von Quantentheorie:
Energie bzw. Strahlungsabsorption nur in Quanten, entsprechend gibt es nur
diskrete Energie- und Schwingungszustände, die nicht äquidistant sind:
IR-Spektroskopie - 01
6
Spektroskopie in der Organischen Chemie
(gestrichelt: Potenzialverlauf des harmonischen Oszillators)
Oberschwin
gungen
Schrödinger-Gleichung -> Formel für die Energie der
Molekülschwingungszustände (Evib):
Evib = hνosc(n+1/2) = h/(2π) (k/µ)1/2(n+1/2)
n = Schwingungsquantenzahl (v in der Abbildung) = 0, 1, 2 ...
n = 0 nach n = 1 -> Grundschwingung
n = 0 nach n = 2 -> 1. Oberschwingung usw.
IR-Spektroskopie - 01
7
Spektroskopie in der Organischen Chemie
Auswahlregeln und Bandenintensität
1) quantenmechanisch: Δn (bzw. Δv) = ±1, ±2, ±3, ...
2) Es gilt generell, dass Absorption und Emission von elektromagnetischer
Strahlung nur dann möglich sind, wenn sie mit einer Änderung des
Dipolmomentes des Moleküls einhergehen.
IR-Licht kann also nur dann absorbiert werden, wenn der elektrische
Lichtvektor mit dem Dipolmoment des Moleküls, oder zumindest des
schwingenden Teils des Moleküls in Wechselwirkung treten kann. Dazu muß
sich das Dipolmoment in einem Extrem der Schwingung von dem im anderen
unterscheiden.
Für symmetrische Schwingungen ist diese Bedingung nicht gegeben, sodass
diese IR-inaktiv sind.
Im Gegensatz dazu tritt der RAMAN-Effekt (Streuemission im IR-Bereich) nur
dann auf, wenn die betreffende Schwingung die Polarisierbarkeit des Moleküls
ändert, welche ein Maß für die Deformierbarkeit der Elektronenwolke darstellt.
Dies ist gerade bei symmetrischen Schwingungen der Fall.
IR-Spektroskopie - 01
8
Spektroskopie in der Organischen Chemie
aus: Biological applications of synchrotron radiation infrared spectromicroscopy
Augusto Marcellia, , , Antonio Cricentib, Wojciech M. Kwiatekc, Cyril Petiboisd
Biotechnology Advances Volume 30, Issue 6, November–December 2012, Pages 1390–1404
In animierter Form zum Beispiel unter:
http://teaching.shu.ac.uk/hwb/chemistry/tutorials/molspec/irspec1.htm
IR-Spektroskopie - 01
9
Spektroskopie in der Organischen Chemie
Die Intensität I einer IR-Bande ist proportional zum Quadrat der Dipolmomentsänderung bei der Schwingung:
 ∂µ 

 ∂r 
2
I =
Ist innerhalb einer Gruppe das Dipolmoment groß (z.B. C=O), kommt es auch
zu großen Änderungen, und die IR-Bande für die Schwingung ist stark.
Es ist also i.a. nicht möglich, IR-Banden quantitativ auszuwerten und aus ihrer
Intensität auf die Zahl der betreffenden Gruppen im Molekül rückzuschließen.
Semiquantitative Bestimmung der Konzentration basierend auf dem LambertBeerschen Gesetz und einer Eichkurve möglich (s. Hesse, Meier Zeeh).
Messung von IR-Spektrum: möglich an
- Gasen – Spezialzelle, NaCl-Plättchen (ok: 4000-667 cm-1) an Enden
- Flüssigkeiten – Tropfen zwischen NaCl-Plättchen (Achtung: H2O)
- Feststoffen – Suspension in Öl (Paraffin) oder KBr-Pressling
IR-Spektroskopie - 01
10
Spektroskopie in der Organischen Chemie
Strukturabhängigkeit der Carbonyl-Schwingung (νC=O)
Abnahme des elektronenziehenden Effekts der Substituenten
F2C=O
Cl2C=O
(Alkyl)2C=O
ν~
1928
1827
1710
Verkleinerung der Wellenzahl
Cl
H3C C
ν~
O
cm-1
R
H3C C
O
1815 – 1790
O
1750 – 1735
cm-1
C=O: hohes Dipolmoment, Neigung zu intra- und intermolekularen WW
IR-Spektroskopie - 02
1
Spektroskopie in der Organischen Chemie
Ringgröße und -spannung
O
ν~
1775
O
1750
O
O
1715
1705
cm-1
Konjugation führt zu kleineren Wellenzahlen:
O
R1
ν~
O
R2
1710
IR-Spektroskopie - 02
R1
O
R2
1680
R1
R2
1650
cm-1
2
Spektroskopie in der Organischen Chemie
C-H-Valenzschwingungen (νCH)
(Schematische Darstellung)
-> je nach Strukturelement charakteristische Positionen
IR-Spektroskopie - 02
3
Spektroskopie in der Organischen Chemie
OH-Banden (νO-H; Wasser, Alkohole)
Konzentrationsabhängigkeit
reiner Alkohol
Lösung - konzentriert
Lösung verdünnt
freies OH
ca. 3600 cm -1
freies OH
ca. 3600 cm -1
aliphat. CH
3000-2900 cm -1
gebundenes OH
ca. 3400
IR-Spektroskopie - 02
cm -1
gebundenes OH
ca. 3400 cm -1
4
Spektroskopie in der Organischen Chemie
Intramolekulare H-Brücken können durch Verdünnungsexperimente von
intermolekularen unterschieden werden. Sie bleiben auch bei hoher Verdünnung bestehen, während die aus intermolekularen H-Brücken zusammenbrechen, und nur die schmale Bande bei 3650 - 3590 cm-1 übrigbleibt.
H
O
C
H
O
H
H
O
C
C
O
H
O
O
H
IR-Spektroskopie - 02
p-Hydroxybenzaldehyd
Salicylaldehyd
(intermolekulare H-Brücken)
(intramolekulare H-Brücken)
5
Spektroskopie in der Organischen Chemie
Bandenverschiebung durch Isotope
In erster Näherung kann die Frequenz eines schwingenden Oszillators mit den
beiden Massen m1 und m2 durch das Hookesche Gesetz beschrieben werden:
1
ν~osz =
2π
k
µ
µ=
m1 ⋅ m2
m1 + m2
k ist die Kraftkonstante und µ die reduzierte Masse:
Will man die Verschiebung einer IR-Bande durch Isotopenaustausch (Isotop 1 →
Isotop 2; z.B. O-H → O-D) abschätzen, nimmt man (stark vereinfachend) an,
dass die Kraftkonstante k beider Bindungen gleich ist.
Dann kann man ansetzen:
ν~1
IR-Spektroskopie - 03
ν~2 =
1
1
µ1
=
µ2
µ1
µ2
1
Spektroskopie in der Organischen Chemie
Abschätzung:
Die Wellenzahl der OH-Schwingung von Methanol (CH3OH) im Gaszustand ist
3681 cm-1. Wie groß ist die von Deuteromethanol (CD3OD)?
1/µ 1 = 1/1 + 1/16 = 1.0625
1/µ 2 = 1/2 + 1/16 = 0.5625
ν~1
ν~2 = 1.3744
ν~1 = 3681 cm -1
ν~2 = 2678 cm -1
Gemessen wurden 2718 cm-1. Die Abweichung ist auf nicht ganz exakt gleiche
Kraftkonstanten und auf die Anharmonizität der Schwingung zurückzuführen.
IR-Spektroskopie - 03
2
Die reduzierte Masse μ
Was hat es eigentlich mit der sogenannten reduzierten Masse μ auf sich?
m 1 m2
μ =
m1 + m2
Sie taucht immer wieder bei der Formelbeschreibungen von Bewegungsvorgängen mehratomiger
Moleküle auf. Im einfachsten Fall, bei hantelförmigen Körpern (Abb. 1), die aus zwei Massenpunkten m1 und m2 mit einem Abstand r bestehen, ist sie wie oben angegeben definiert.
Bewegungsvorgänge eines solchen Körpers (Rotation, Schwingung) werden dann durch Formeln
beschrieben, die aus der klassischen Mechanik für Massenpunkte m kommen, in denen diese aber
durch μ ersetzt wird.
Woher kommt dieser umständlich erscheinende Ausdruck für μ? Wir wollen ihn zunächst für den
starren Rotator ableiten.
Rotation eines zweiatomigen Moleküls
Stellen wir uns ein zweiatomiges Molekül als Hantel mit zwei Massen m1 und m2 vor, die durch
eine starre Verbindung der Länge r0 (Atombindung) miteinander verbunden sind:
Abb. 1
r0
C
m2
m1
r1
r2
Dieser Körper soll um eine Querachse rotieren, die die Atomverbindung (r0) an derjenigen Stelle
schneidet, die durch „C“ markiert ist.
r0 = r1 + r2
(1)
C ist der Schwerpunkt (vgl. Waage oder Hebelgesetze); er ist definiert durch:
m1 r1 = m2 r2
(2)
Das Trägheitsmoment für diese Rotation ist:
Θ = m1 r12 + m2 r22
(3)
oder mit Gleichung (2)
Θ = m2 r2 r1 + m1 r1 r2
= r1 r2 (m1 + m2)
(4)
Aus der Kombination der Gleichungen (1) und (2) ergibt sich:
m1 r1 = m2 r2 = m2 (r0 – r1)
(5)
1
und daraus
r1 =
m2 r0
und
m1 + m2
m1 r0
r2 =
(6)
m1 + m2
Einsetzen der Gleichungen (6) in Gleichung (4) ergibt:
Θ
also:
μ =
m1 m2
m1 + m2
m1 m2
=
m1 + m2
r0 2
und daraus
(1)
=
μ r0 2
(7)
1/μ = 1/m1 + 1/m2
(8)
Das Trägheitsmoment für die Rotation eines Massenpunktes m ist
Θ = m r0 2 .
(9)
Wir haben für den Übergang von einem Massenpunkt m zu einer Hantel nichts weiter getan, als
die Masse m in Gleichung (9) durch die reduzierte Masse μ zu ersetzen.
Gleichung (7) definiert das Trägheitsmoment eines hantelförmigen Körpers (zweiatomigen Moleküls) als Funktion der beiden Einzelmassen und ihrem Abstand.
Die reduzierte Masse repräsentiert dabei die Summe aller Einzelmassen
in einer starren Hantel
und für sie gilt laut Gleichung (8):
Die reziproke reduzierte Masse ist gleich den Summe der reziproken Einzelmassen.
Schwingung eines zweiatomigen Moleküls
Der Ersatz von m durch μ lässt sich analog auch für andere Bewegungsarten einer Hantel ableiten.
Betrachten wir zuerst die longitudinale Schwingung einer Masse, die mit einer Feder fest aufgehängt ist und um einen Ruheabstand r0 herum schwingt (Abb. 2):
Abb. 2
r0
m
Diese Bewegung wird durch das Hookesche Gesetz (10) beschrieben. Ihre Frequenz ν ist:
ν =
1
2π
k
m
(10)
wobei k die Kraftkonstante der Feder ist.
2
Gehen wir nun zur Valenzschwingung über, bei der die beiden Massen m1 und m2 auf der
Kernverbindungslinie (kovalente Bindung; Abb. 1) gegeneinander schwingen (Oszillator), sich
der Abstand r also fortlaufend ändert, d.h. um einen Optimalwert r0 herum schwingt. Auch dafür
existiert eine Kraftkonstante k; beim zweiatomigen Molekül ist das die Bindungsstärke.
Ganz analog zum Fall des Rotators wird dann wieder die Masse m des in Abb. 2 dargestellten
Oszillators durch die reduzierte Masse ersetzt:
ν =
1
2π
k
μ
(10)
Man beachte jedoch, dass diese Ableitung nach den Gesetzen der klassischen Mechanik das
wirkliche Schwingungsverhalten nur sehr unvollständig beschreibt, denn sie gibt die Parabelform
vor. Sie sollte nur für Schwingungen mit niedrigen Amplituden herangezogen werden. Bei höheren wird das Schwingungsverhalten eher durch eine unsymmetrische Potenzialkurve beschrieben, die – in Übereinstimmung mit den beobachteten Fakten – einen Bindungsbruch zulässt.
Außerdem ist die atomare Schwingung natürlich den Gesetzen der Quantenmechanik unterworfen, was bedeutet, dass nur bestimmte Amplituden (Schwingungsquanten) zur Verfügung stehen.
3