Übungsblatt 2 - Lehrstuhl für Optik, Uni Erlangen

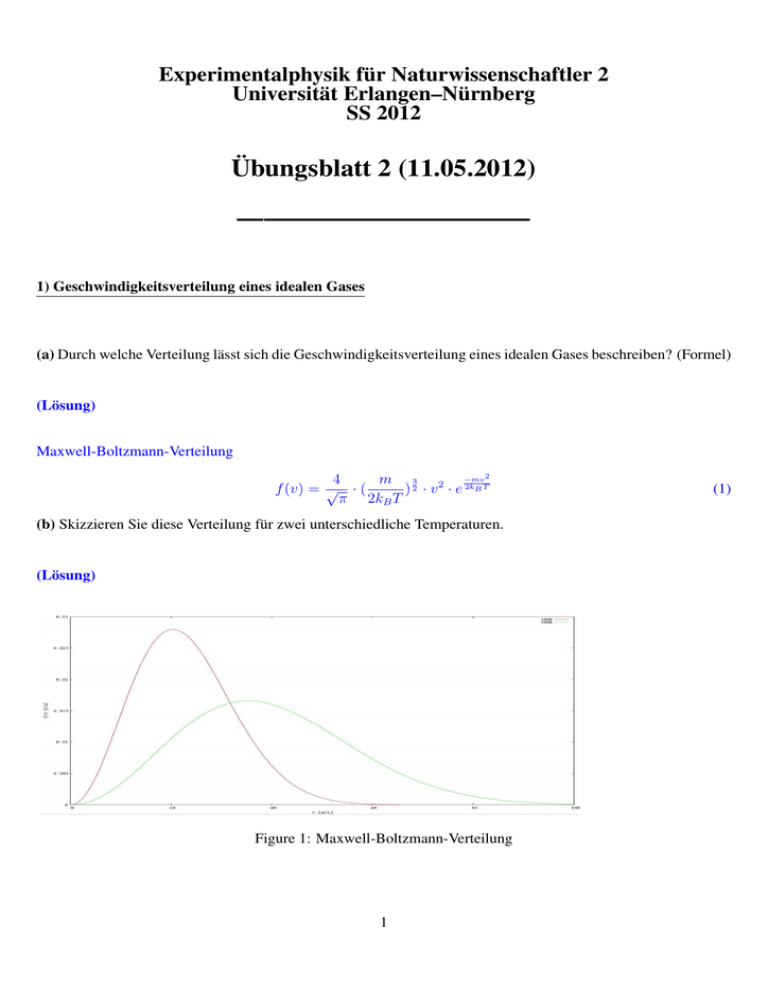
Experimentalphysik für Naturwissenschaftler 2
Universität Erlangen–Nürnberg
SS 2012
Übungsblatt 2 (11.05.2012)
———————————
1) Geschwindigkeitsverteilung eines idealen Gases
(a) Durch welche Verteilung lässt sich die Geschwindigkeitsverteilung eines idealen Gases beschreiben? (Formel)
(Lösung)
Maxwell-Boltzmann-Verteilung
2
4
m 3 2 −mv
f (v) = √ · (
) 2 · v · e 2kB T
π 2kB T
(b) Skizzieren Sie diese Verteilung für zwei unterschiedliche Temperaturen.
(Lösung)
Figure 1: Maxwell-Boltzmann-Verteilung
1
(1)
Wie verhalten sich die Extrema bei unterschiedlichen Temperaturen?
Welchen Wert hat das Integral über den gesamten Definitionsbereich?
Wie berechnet man die Wahrscheinlichkeit, dass ein Teilchen eine Geschwindigkeit zwischen den Punkten
v1 und v2 besitzt?
(Lösung)
Die Kurve wird für größere Temperaturen breiter und flacher und weiterhin wandert das Extremum der Kurve
hin zu größeren Geschwindigkeiten.
Das Integral über den gesamten Definitionsbereich beträgt 1.
Die Wahrscheinlichkeit ergibt sich zu:
v2
Z
f (v)dv
W =
(2)
v1
mit f(v) aus (1)
(c) Berechnen Sie die wahrscheinlichste Geschwindigkeit von Helium, unter Zuhilfenahme von oben genannter
Verteilung, bei T = 150◦ C.
g
.
Die molare Masse von Helium beträgt 4 mol
(Lösung)
2
4
m 3 2 −mv
2
f (v) = √ · (
) 2 · v · e 2kB T = a · v 2 · e−bv
π 2kB T
mit a =
√4
π
3
· ( 2kmB T ) 2 und b =
(3)
m
2kB T
df (v)
2
2
= a · 2 · v · e−bv + a · v 2 · e−bv (−b) · 2 · v
(4)
dv
Die wahrscheinlichste Geschwindigkeit entspricht dem Maximum der Verteilung. Weshalb die Ableitung nun
Null gesetzt wird.
2
2
2 · a · v · e−bv − 2 · a · b · v 3 · e−bv = 0
Aus R = NA · kB und MHe
definiert ist)folgt:
(5)
1 − b · v2 = 0
(6)
r
r
1
2kB T
v=
=
(7)
b
m
= m · NA (da die molare Masse als Masse eines Teilchen · Avogadro-Konstante
r
v=
2
2RT
MHe
(8)
Eingesetzt ergibt sich:
s
=
J
2 · 8, 314 mol·K
· 150◦ C
=
g
4 · mol
s
J
2 · 8, 314 mol·K
· (150 + 273)K
4·
kg
10−3 mol
= 1326
m
s
(9)
(d) Berechnen Sie die mittlere Geschwindigkeit von Helium bei T = 150◦ C.
(Lösung)
Aus der Vorlesung ist bekannt, dass für die mittlere Geschwindigkeit gilt:
r
8 · kB · T
v=
π·m
Ersetzt man hierbei nun wieder wie oben kB =
R
NA
r
v=
(10)
und MHe = m · NA dann gilt:
m
8·R·T
= 1496
π · MHe
s
(11)
Berechnen Sie außerdem die mittlere freie Weglänge und die mittlere Zeit zwischen zwei Stößen.
kg
Der Stoßquerschnitt von Helium beträgt 30 · 10−16 cm2 und die Dichte des komprimierten Heliums ist 0, 3 m
3.
(Lösung)
x=
1
=
ρn · σ
mit v aus (11) folgt:
τ=
1
ρ·NA
MHe
·σ
= 7, 4 · 10−8 m
x
= 4, 9 · 10−11 s
v
(12)
(13)
2) Wärmeaustausch
kJ
).
Ein Topf voll Wasser (5l) soll von 20◦ auf 30◦ erhitzt werden (cW asser = 4, 18 kgK
(a) Wie viel Energie muss dem Wasser hinzugegeben werden, um dieses aufzuheizen?
Hinweis: Vernachlässigen Sie die Energie, die benötigt wird, um den Topf zu erhitzen.
(Lösung)
Um den Wärmeaustausch zu berechnen, benötigt man die Masse des Wassers. Diese ergibt sich daraus, dass 5l
Wasser 5kg wiegen.
Q = mW asser · cW asser · ∆T = 5kg · 4, 18
3
kJ
· (30 − 20)K = 209kJ
kgK
(14)
(b) Welche Masse an heißem Eisen (T = 90◦ C) würde das Wasser auf die gleiche Temperatur erhitzen?
kJ
(cF e = 0, 46 kgK
)
(Lösung)
Die Energie, die dem Wasser zugeführt werden muss, um es auf 30◦ C zu erhitzen, muss also dem Eisen entzogen
werden. Da das Eisen danach die gleiche Temperatur wie das erhitzte
haben muss (thermodynamisches
Wasser
0
◦
Gleichgewicht), gilt also für die Temperaturänderung des Eisens: ∆T = 90 C − 30◦ C = 60K.
somit ergibt sich:
0
Q = 209kJ = mF e · cF e · ∆T
(15)
mF e =
209kJ
|Q|
= 7, 6kg
0 =
kJ
cF e · ∆T
0, 46 kgK
· 60K
(16)
(c) Wie viel Eisen aus Aufgabe (b) wird benötigt, wenn man berücksichtigt, dass der Topf auch auf 30◦ C erhitzt
kJ
werden muss? (cT opf = 0, 77 kgK
; mT opf = 1kg; TT opf = 20◦ C)
(Lösung)
Q = mT opf · cT opf · ∆T = 1kg · 0, 77
mF e =
kJ
· (30 − 20)K = 7, 7kJ
kgK
|Qgesamt |
216, 7kJ
= 7, 85kg
0 =
kJ
cF e · ∆T
0, 46 kgK
· 60K
(17)
(18)
3) Kreisprozess
Wir betrachten einen Kreisprozess, der aus einer isochoren Abkühlung, einer isobaren Expansion und einer
isothermen Kompression besteht.
Die isochore Abkühlung startet bei 12 bar und 3 l (Punkt A). Danach beträgt die Temperatur 25 K (Punkt B).
Während der isobaren Expansion dehnt sich das Volumen auf 12 l aus (Punkt C).
(a) Berechnen Sie für jeden Eckpunkt (A, B, C) die Werte für V, p und T und zeichnen Sie ein P-V-Diagramm.
(Lösung)
Die gegebenen Werte sind:
Punkt V
P
T
A
3 l 12 bar
B
25 K
C
12 l
Aus der isochoren Abkühlung folgt: VA = VB = 3l.
Aus der isobaren Expansion folgt: pB = pC =: p, wobei der Zahlenwert unbekannt ist.
Aus der isothermen Kompression gilt: TC = TA =: T , wobei auch hier der Zahlenwert unbekannt ist.
4
Somit sieht die Tabelle, wenn man das oben genannte berücksichtigt, folgendermaßen aus:
Punkt V
P
T
A
3 l 12 bar
T
B
3l
p
25 K
C
12 l
p
T
Es fehlen also nur noch zwei Werte, nämlich p und T, die man nun über die ideale Gasgleichung berechnen kann.
Hierfür stellen wir erst einmal die ideale Gasgleichung für die drei Einzelschritte auf:
Für den Schritt A → B gilt: pTA = TpB .
Für den Schritt B → C gilt: VTBB = VTC .
Hierbei sieht man sofort, dass in der zweiten Gleichung die einzige Unbekannte T ist.
Daraus folgt, dass T = 100K ist.
Nun kann man entweder die dritte Gleichung C → A aufstellen und daraus p berechnen:p · VC = pA · VA .
Oder man setzt das bereits ausgerechnete T in die erste Gleichung wieder ein und berechnet so p.
Für p ergibt sich: p = 3bar.
Jetzt ist unsere Tabelle komplett und sieht folgendermaßen aus:
Punkt V
P
T
A
3 l 12 bar 100K
B
3l
3 bar
25K
C
12 l 3 bar 100K
Alle fett geschriebenen Werte sind angegeben, die kursiv geschriebenen lassen sich über die Beziehungen der
Teilschritte erschließen und die übrigen Werte werden über die ideale Gasgleichung berechnet.
Figure 2: P-V-Diagramm
5
(b) Berechnen Sie für diesen Kreisprozess den Wärmetransport, die verrichtete Arbeit sowie die Änderung der
inneren Energie pro Teilschritt und für den gesamten Kreisprozess.
(Lösung)
Zuerst muss die Stoffmenge berechnet werden:
n·R·T =P ·V
n=
P ·V
12bar · 3l
12 · 105 pa · 3 · 10−3 m3
=
=
= 4, 33mol
J
J
R·T
8, 314 mol·K
· 100K
8, 314 mol·K
· 100K
(19)
(20)
Somit gilt für die einzelnen Teilschritte:
1) isochore Abkühlung:
∆W1 = 0
3
∆Q1 = ∆U1 = n · CV · ∆T = n · · R · (25 − 100)K = −4, 05kJ
2
(21)
∆W2 = −p · ∆V = −3bar · (12 − 3)l = −2, 7kJ
(23)
(22)
2) isobare Expansion
3
· R · (100 − 25)K = 4, 05kJ
2
∆Q2 = ∆U2 − ∆W2 = 4, 05kJ + 2, 7kJ = 6, 75kJ
∆U2 = n · CV · ∆T = n ·
(24)
(25)
3) isotherme Kompression
∆T = 0 ⇒ ∆U3 = 0
(26)
Z
VE
VE
dV
VA
12l
= n·R·T ·ln( ) = 4, 33mol·R·100K·ln( ) = 4, 99kJ
⇒ −∆Q3 = ∆W3 = −
pdV = −n·R·T ·
V
VE
3l
VA
VA
(27)
Und für den gesamten Kreisprozess ergibt sich:
Z
U
Teilschritt
kJ
1
-4,05
2
4,05
3
0
gesamt
0
Q
kJ
-4,05
6,75
-4,99
-2,29
W
kJ
0
-2,7 ∆Ugesamt = 0, da die innere Energie bei einem Kreisprozess erhalten bleibt.
4,99
2,29
6
(c) Berechnen Sie auch den Wirkungsgrad dieses Prozesses und vergleichen Sie diesen mit dem Carnot-Wirkungsgrad.
(Lösung)
Der Wirkungsgrad berechnet sich wie folgt:
η=
Enutz
|Wges |
2, 29kJ
=
=
= 0, 34
Ein
|Q2 |
6, 75kJ
(28)
Für den Carnot-Wirkungsgrad gilt:
ηCarnot =
100K − 25K
T2 − T1
=
= 0, 75
T2
100K
(29)
Man sieht, dass ηCarnot > η.
Achtung!
Dieser Kreisprozess macht vom physikalischen Standpunkt aus keinen Sinn.
Dies liegt daran, dass im Endeffekt Arbeit gebraucht wird um Wärme vom Wärmebad ins Kältebad zu
transportieren, was nicht sonderlich praktisch ist, da dieser Prozess auch ohne vorher eingespeiste Arbeit
ablaufen würde.
Im Detail heißt das dann, dass im Teilschritt 1 das angeschlossene Kältebad aufgeheizt wird (Wärme geht aus
dem Kreisprozess hinaus). Im Teilschritt 2 wird daraufhin das Wärmebad angeschlossen, welches Energie
verliert und wodurch Nutzarbeit frei wird. Jetzt ist aber das Problem, dass diese gewonnene Nutzarbeit im
Teilschritt 3 mehr als aufgebraucht wird und weiterhin ist es auch dort nur möglich dem Wärmebad einen Teil
seiner ursprünglichen Energie zurückzuführen.
Deshalb ist der Kreisprozess an sich sinnlos, um die Rechnungen zu üben aber vielleicht doch ganz hilfreich.
Ein weiterer Punkt ist auch, da aufgrund der positiven Gesamtarbeit ein Wirkungsgrad keinen Sinn macht. Da
somit das System nicht als Wärmekraftmaschine zu betrachten ist. Eine Betrachtung als Kühlmaschine ist
ebenso nicht möglich, da eben das Kältebad aufgeheizt wird.
Was man aber nun machen kann um den Kreisprozess noch zu retten ist, dass man ihn einfach in die andere
Richtung laufen lässt. Somit kehren sich alle Vorzeichen der Energien um (da die ∆ T’s und auch der Term
ln( VVEA )) die Vorzeichen vertauschen).
Also bekommt man vom System geleistete Arbeit (negatives Vorzeichen) indem man Wärme in das System
hineinbringt.
Um den Wirkungsgrad der umgekehrten Richtung zu berechnen muss man jetzt noch beachten, dass 2mal
Wärme in den Kreisprozess hineingeführt wird. Und zwar einmal bei der isothermen Expansion und bei der
isochoren Erwärmung. Somit ergibt sich dann die gesamte eingebrachte Energie als die Summe der einzelenen
Wärmen.
η=
|Wges |
2, 29kJ
Enutz
=
=
= 0, 25
Ein
|Qgesamt |
4, 05kJ + 4, 99kJ
7
(30)