Übung: Algorithmen und Datenstrukturen SS 2007

Übung: Algorithmen und Datenstrukturen
SS 2007
Prof. Lengauer
Sven Apel, Michael Claÿen, Christoph Zengler, Christof König
Blatt 8
Votierung in der Woche vom 25.06.0729.06.07 Aufgabe 22
AVL-Bäume
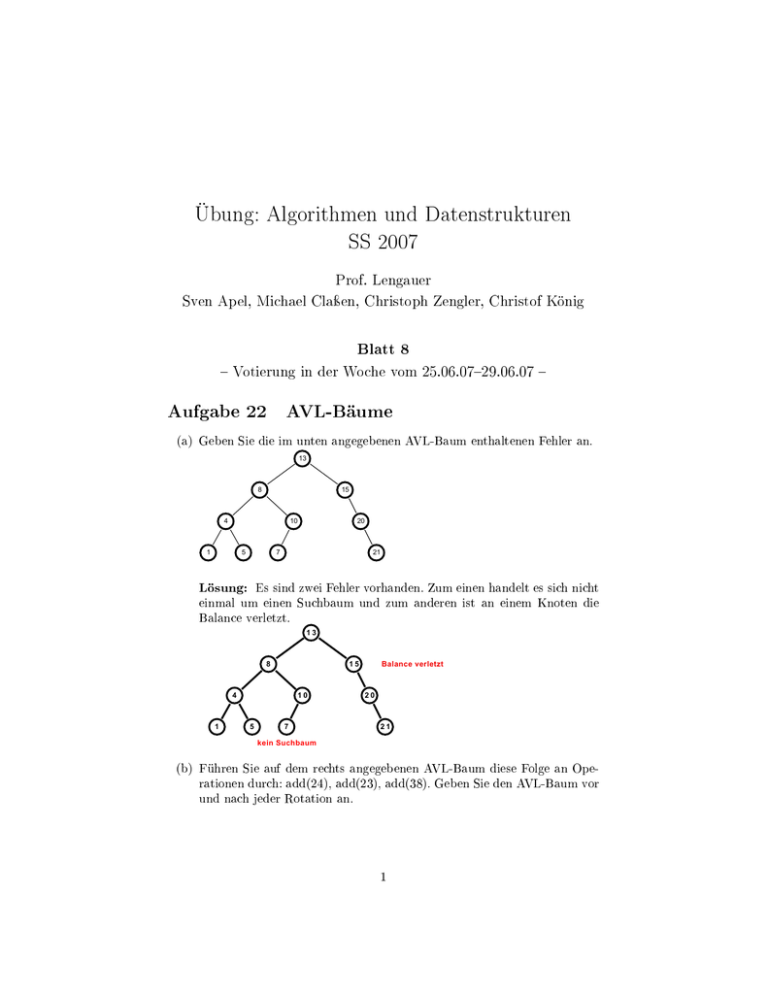
(a) Geben Sie die im unten angegebenen AVL-Baum enthaltenen Fehler an.
13
8
15
4
10
1
5
20
7
21
Lösung: Es sind zwei Fehler vorhanden. Zum einen handelt es sich nicht
einmal um einen Suchbaum und zum anderen ist an einem Knoten die
Balance verletzt.
13
8
15
4
1
10
5
7
Balance verletzt
20
21
kein Suchbaum
(b) Führen Sie auf dem rechts angegebenen AVL-Baum diese Folge an Operationen durch: add(24), add(23), add(38). Geben Sie den AVL-Baum vor
und nach jeder Rotation an.
1
30
20
10
50
25
35
33
55
37
Lösung: Der Knoten 24 kann problemlos hinzugefügt werden, die Balance bleibt an allen Knoten erhalten.
30
20
10
50
25
35
24
33
55
37
Der Knoten 23 sorgt dafür, dass bei 24 und 25 jeweils eine negative Balance auftreten, also der linken Teilbaum ist jeweils tiefer als der rechte
Teilbaum. Um dies zu korrigieren wird eine Rechtsrotation an 25 durchgeführt. Man erhält:
30
20
10
50
24
23
35
25
33
55
37
Der letzte Knoten 38 führt dazu, dass beim Knoten 50 die Balance verletzt ist. Knoten 50 hat einen tieferen linken Sohn und Knoten 35 einen
tieferen rechten Sohn. Damit ist zunächst eine Linksrotation an 35 und
anschlieÿend eine Rechtsrotation an 50 notwending, um die Balance wieder herzustellen.
30
20
10
37
24
23
35
25
33
50
38
55
2
Aufgabe 23
2-3-Bäume
(a) Fügen Sie manuell in einen leeren 2-3-Baum die folgenden Zahlen ein:
8, 9, 10, 2, 1, 5, 3, 6, 4
Geben Sie den entstehenden Baum nach jeder Operation an. Geben Sie die
nötigen Zwischenschritte an, falls ein Knoten aufgespalten werden muss.
Lösung: Zunächst einmal ganz allgemein:
Daten stehen nur an den Blättern.
Alle Blätter sind gleich tief.
Innere Knoten haben einen Schlüssel und zwei Zeiger oder zwei Schlüssel und drei Zeiger.
Suchen in einem 2-3-Baum: Bei einem Schlüssel wie im binären Suchbaum
(Falls Suchwert = Schlüssel nach rechts gehen). Bei 2 Schlüsseln: 1. Zeiger:
Werte < 1. Schlüssel, 2. Zeiger: Werte = 1. Schlüssel, kleiner 2. Schlüssel
und 3. Zeiger: Werte = 2. Schlüssel.
Einfügen: Suche den passenden inneren Knoten, an dem Blätter hängen.
Füge dort den passenden neuen Schlüssel ein und hänge ein neues Blatt
dazu. Falls der Knoten jetzt 3 Schlüssel hat, spalte den Knoten in drei
Teile: der mittlere Schlüssel wandert im Baum nach oben (und erzeugt
dort evtl. wieder ein Spalten), die beiden anderen Schlüssel werden neue
innere Knoten (mit jeweils einem Schlüssel). Jeder dieser Knoten hat dann
2 Zeiger.
Innere Knoten werden als Kasten gezeichnet, Blätter dagegen ohne Rahmen. Problemfall: nur ein Knoten vorhanden. Dann kann es keinen inneren
Knoten geben, da ein solcher mindestens zwei Blätter hätte, aber nur ein
Datum vorhanden ist.
8
-- -- -| 8| 9|10|
-- -- -| | | |
2 8 9 10
-| 9|
-| |
8 9
-- -| 9|10|
-- -| | |
8 9 10
-| 9|
->
-/
\
--| 8|
|10|
--| |
| |
3
2
8
9
10
-| 9|
-/
\
-- --| 2| 8|
|10|
-- --| | |
| |
1 2 8
9 10
-| 9|
-/
\
-- -- --| 2| 5| 8|
|10|
-- -- --| | | |
| |
1 2 5 8
9 10
->
-- -| 5| 9|
-- -/
| \
-- ---| 2| 3| | 8| |10|
-- ---| | | | | | |
1 2 3 5 8 9 10
/
-- -- -| 2| 3| 4|
-- -- -| | | |
1 2 3 4
-- -| 5| 9|
-- -|
-- -| 6| 8|
-- -| | |
5 6 8
-- -| 5| 9|
-- -/ |
\
---| 2| | 8| |10|
---| | | | | |
1 2 5 8 9 10
-- -| 5| 9|
-- -/ |
\
/
|
\
-- --- -- -| 2| 3| | 6| 8| |10|
-- -- -- --| | | | | | | |
1 2 3 5 6 8 9 10
\
-|10|
-| |
9 10
-| 5|
4
->
-- -- -| 3| 5| 9|
-- -- -/
| |
\
-- --- -| 2| | 4| | 6| 8|
-- --- -| | | | | | |
1 2 3 4 5 6 8
-|10|
-| |
9 10
->
-/
\
--| 3|
| 9|
--/
|
|
\
--- -- --| 2| | 4| | 6| 8| |10|
--- -- --| | | | | | | | |
1 2 3 4 5 6 8 9 10
(b) Führen Sie folgende Operationen auf dem Baum aus, welcher in Teilaufgabe (a) erzeugt wurde.
1. Löschen Sie die 6.
Lösung: Löschen: Suche das Blatt. Lösche es und den Schlüssel
darüber. Hat dieser Knoten nun nur noch einen Sohn, prüfe, ob ein
Bruder einen Sohn abgeben kann (falls dieser 3 hat). Ansonsten verschmelze Knoten mit einem Bruder und dem Schlüssel des Vaters zwischen den Brüdern. Dadurch verliert der Vater wieder einen Schlüssel
(evtl. bis zur Wurzel => der Baum wird niedriger). Passe Schlüssel
bis zur Wurzel an.
Lösche die 6, der Vater hat immer noch zwei Söhne.
-| 5|
-/
\
--| 3|
| 9|
--/
|
|
---| 2| | 4| | 8|
---| | | | | |
1 2 3 4 5 8
\
-|10|
-| |
9 10
2. Löschen Sie die 5.
Lösung: Lösche die 5 und den Schlüssel 6 darüber, der Knoten hat
5
noch 2 Söhne. Ändere den Schlüssel 5 an der Wurzel auf 6 (dies ist
evtl. nicht notwendig, hängt von der konkreten Invariante ab.
-| 5|
-/
\
--| 3|
| 9|
--/
|
|
---| 2| | 4| | 8|
---| | | | | |
1 2 3 4 6 8
\
-|10|
-| |
9 10
3. Löschen Sie die 9.
Lösung: Lösche 9. Vater hat nur noch den Sohn 10. Linker Bruder hat drei Söhne (5,6,8). Die 8 wandert zum betrachteten Knoten.
Von der neuen Position der 8 nach oben müssen Schlüssel angepasst
werden (je nach Invariante, siehe oben.
-| 5|
-/
\
--| 3|
| 8|
--/
|
|
\
--- --| 2| | 4| | 6|
|10|
--- --| | | | | |
| |
1 2 3 4 5 6
8 10
4. Löschen Sie die 1.
Lösung:
--
6
| 5|
-/
\
--| 3|
| 9|
--/
|
|
\
--- -- --| 2| | 4| | 6| 8| |10|
--- -- --| | | | | | | |
2 3 4 5 6 8 9 10
Bruder kann keinen Sohn abgeben => verschmelze mit Bruder und
Schlüssel des gemeinsamem Vaters zwischen den Werten:
-| 5|
-/
\
--| ?|
| 9|
--/
|
\
-- --- --| 3| 4| | 6| 8| |10|
-- --- --| | |
| | | | |
2 3 4
5 6 8 9 10
Vater hat nun einen Knoten zuwenig, wieder verschmelzen:
-- -| 5| 9|
-- -/
|
-- -- -- -| 3| 4| | 6| 8|
-- -- -- -| | | | | |
2 3 4 5 6 8
\
-|10|
-| |
9 10
Geben Sie das Ergebnis jeder Löschoperation an.
7
Aufgabe 24
Minimaler Grad von B-Bäumen
(a) Weshalb lassen wir für den minimalen Grad eines B-Baums t = 1 nicht
zu?
(b) Für welche Werte des minimalen Grades t ist der folgende Baum ein zulässiger B-Baum?
(c) Zeichnen Sie alle zulässigen B-Bäume mit minimalen Grad 2, die die Menge
{1, 2, 3, 4, 5} darstellen!
Lösung:
(a) Laut Denition müsste in Falle t = 1 jeder Knoten auÿer der Wurzel mindestens keine und höchstens einen Schlüssel enthalten. Damit hätten wir erstens die
Möglichkeit leerer Knoten gegeben, was a) keinen Sinn macht und b) zu Problemen führt. Zweitens hätten wir im besten Fall einen Binärbaum deniert, den
wir auch einfacher hätten denieren können.
(b) Zulässige Werte von t sind 2 und 3. Im Fall t = 2 gilt, dass jeder Knoten
auÿer der Wurzel mindestens t − 1 = 1 Schlüssel enthalten muss und höchstens
2 t − 1 = 3 Schlüssel enthalten darf. Dies ist im Baum oensichtlich erfüllt.
Ebenso gilt dies für t = 3 mit mindestens 2 und höchstens 5 Schlüsseln pro
Knoten. Ab t = 4 ist die Bedingung von mindestens t + 1 Schlüsseln nicht mehr
von allen Knoten erfüllt.
(c)
8
Aufgabe 25
Maximale Anzahl von Schlüsseln im
B-Baum
Wie groÿ ist die maximale Anzahl von Schlüsseln, die in einem B-Baum der
Höhe h gespeichert werden kann. Geben Sie die Anzahl als Funktion des minimalen Grades t an. (Hier ist ein Beweis mittels Induktion gefordert.)
Lösung:
Behauptung: Maximale Anzahl der Schlüssel in einem B-Baum der Höhe h
und mit minimalen Grad t ist
maxKeyt (h) =
h
X
(2t − 1) · (2t)i
i=0
Beweis mit Induktion nach der Höhe des Baumes:
Induktionsanfang h = 0:
Ein Baum mit h = 0 besteht nur aus der Wurzel und hat damit maximal
2t − 1 Schlüssel nach Denition. Dies ergibt auch die Formel maxKeyt (0) =
(2t − 1) · 1 = 2t − 1
Induktionsschritt h → h + 1
P
mit der Induktionsannahme maxKeyt (h) = hi=0 (2t − 1) · (2t)i .
Ein Baum der Höhe h hat maximal (2t)h Blätter (Behauptung ohne Beweis).
Für einen Baum mit Höhe h + 1 gilt also dann, dass er die Anzahl der Schlüssel
des Baums mit Höhe h hat + maximal (2t)h+1 · (2t − 1) neue Schlüssel (jedes
neue Blatt hat maximale Anzahl Schlüssel). Also:
maxKeyt (h + 1) = maxKeyt (h) + (2t)h+1 · (2t − 1)
!
h
X
i
=
(2t − 1) · (2t) + (2t)h+1 · (2t − 1)
i=0
=
h+1
X
(2t − 1) · (2t)i
i=0
Dies war zu zeigen.
9