I. Die Rotation der Sterne

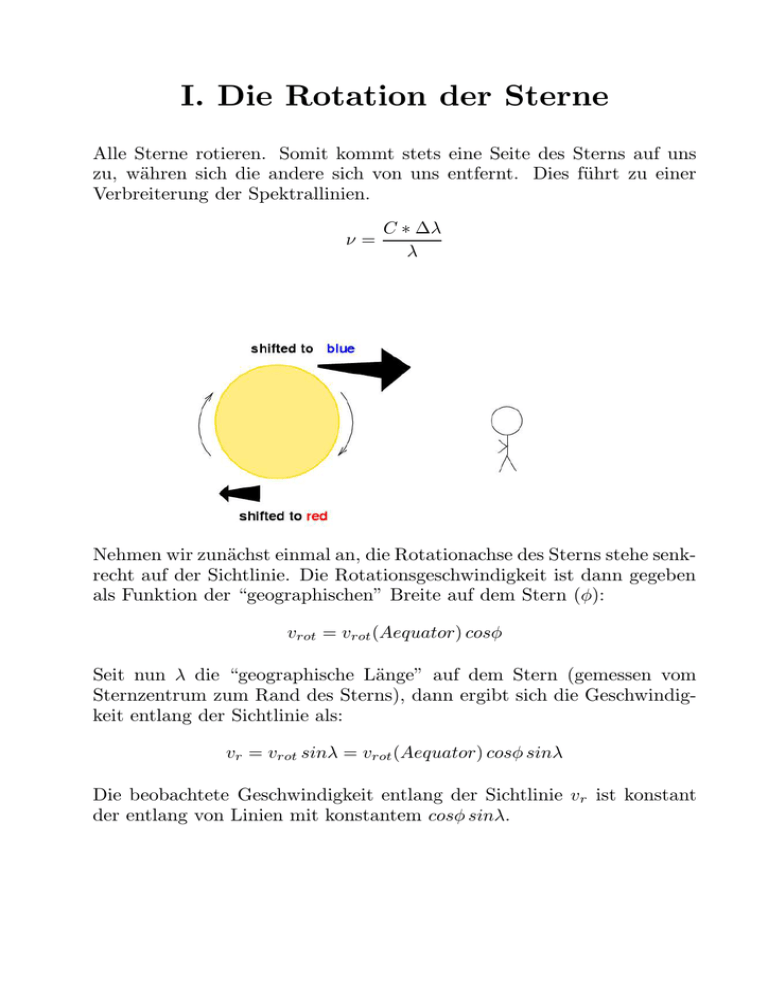
I. Die Rotation der Sterne
Alle Sterne rotieren. Somit kommt stets eine Seite des Sterns auf uns
zu, währen sich die andere sich von uns entfernt. Dies führt zu einer
Verbreiterung der Spektrallinien.
ν=
C ∗ ∆λ
λ
Nehmen wir zunächst einmal an, die Rotationachse des Sterns stehe senkrecht auf der Sichtlinie. Die Rotationsgeschwindigkeit ist dann gegeben
als Funktion der “geographischen” Breite auf dem Stern (φ):
vrot = vrot (Aequator) cosφ
Seit nun λ die “geographische Länge” auf dem Stern (gemessen vom
Sternzentrum zum Rand des Sterns), dann ergibt sich die Geschwindigkeit entlang der Sichtlinie als:
vr = vrot sinλ = vrot (Aequator) cosφ sinλ
Die beobachtete Geschwindigkeit entlang der Sichtlinie vr ist konstant
der entlang von Linien mit konstantem cosφ sinλ.
Jetzt führen wir kartesische Koordinaten ein:
z = r sinφ
x = ρ sinλ
y = ρ cosλ
wobei ρ der Querschnitt durch den Stern bei der “geographischen Breite”
φ ist. r ist der Radius des Sterns.
ρ = r cosφ
Also ergibt sich :
x = r cosφ sinλ
y = r cosφ cosλ
Oben haben wir ja bereits gesehen, dass die Radialgeschwindigkeit vr
konstant entlang von Linien mit konstantem cosφ sinλ ist. Also sind
dies Linien für die x = const gilt. Dies sind also einfach senkrechte
Streifen auf dem Stern!
Steht die Rotationsache des Sterns nicht senkrecht auf der Sichtlinie,
so muß man einfach alle vr -Werte mit sin i multiplizieren, wobei i die
Inklination des Sterns (Winkel zwischen Sichtline und Rotationsachse)
ist.
I.1 Mitte Rand Variation:
Im vorigen Teil haben wir Gleichungen entwickelt um für jeden Punkt der
Sternoberfläche die Geschindigkeit eintlang der Sichtlinie zu bestimmen.
Im Prinzip könnten wir nun fröhlich die Verbreiterung von Spektrallinien
berechnen, aber leider gibt es da ein Problem: Die Mitte Rand Variation.
Leider brauchen wir jetzt ein weitere Koordinate: µ = cosϑ, der Abstand von der Mitte der Sonnenscheibe: µ = 1 (ϑ = 0o ) ist die Mitte
der Sonnenscheibe; µ = 0 ist der Sonnenrand (ϑ = 90o ). Mit dem
Randverdunklungskoeffzient β ergibt sich das Randverdunklungsgesetz
als (β = 0 ist eine leuchtende Scheibe):
1 + β cos ϑ
Iν (ϑ)
=
Iν (0)
1+β
Für die Sonne ist β = 1.5 und v = 2 km s−1 , der Be-Stern ϕ Pers hat ein
v sin i von 560 km s−1 . Die obere Abbildung zeigt die Verbreiterung einer
hypothetischen Linie bei 6811 Å, beobachtet mit einem Spektrographen
mit einer Auflösung von λ/∆λ = 48 000 (FEROS). Die Rotationsverbreiterungen sind für v sin i = 10, 20, 30, 40, 50 km s−1 berechnet worden.
Die untere Abbildung zeigt für v sin i = 50 km s−1 den Effekt der MitteRand Variation. Gerechnet wurde β = 0.2, 0.5, 1.5, 2.5, 3.5, 4.5. Je
größer β ist, um so tiefer ist die Linie . Bei kleinen Werten von β ist das
Profil breiter.
II. Mikro- und Macro-Tubulenz
Auch vor der Beobachtung der Granulation fiel bereits auf, dass Turbulenz in den äusseren Schichten der Sonne ein Rolle spielt.
Mikro-Turbulenz: Zur Messung der chemischen Häufigkeit und der
Temperatur wird häufig die sogenannte Wachstumskurve verwendet. Dabei wird die Äuquivalentbreite gemessener Linien eine Multiplets gegen
log(gf λ) aufgetragen. Der Abstand der Kurven für verschiedene Multiplets liefert dann beispielsweise die Temperatur des Sterns (Eigentlich
χ 5040
T ; χ die Anregungstemperatur). Bei der Analyse der Wachstumskurve am Anfang des 20ten Jhd. fiel auf, dass es für starke Linien eine
Unterschied zwischen gemessener und berechneter Äuquivalentbreite
gibt. Die Differenz konnte mit der Annahme eines turbulenten Geschwindigkeitsfeldes mit einer Amplitude von ξt = 1 − 2 km/s erklärt werden.
Die Linien werden verbreitert durch die Geschwindigkeit der Atome (und
Molekühle) in der Atmosphäre. Diese sogn. Dopplerbreite einer Linie
ist gegeben durch:
q
λ
∆λD =
2vx2
c
...mit Gasgleichung (<=Gaskonstante; mol=Molekulargewicht;
T =absolute Temperatur) ergibt sich daraus:
r
λ 2<T
∆λD =
c mol
...bzw. für die Frequenz:
ν
∆νD =
c
r
2<T
mol
Um nun die brechneten Linienprofile mit der Beobachtung in Einklang
zu bringen, führt man die Turbulenzgeschwindigkeit ξt ein. Diese ist die
sogn. Mikroturbulenz.
r
λ 2<T
+ ξt2
∆λD =
c mol
r
ν 2<T
∆νD =
+ ξt2
c mol
Bei der Sonne ist ξt ∼ 1.4km s−1 .
Makro-Turbulenz: Nachdem die Äquivalentbreiten mit Hilfe der Mikro- Turbulenz “richtig gestellt” wurden, stellte sich bei der Modellierung
der Linienprofile heraus, dass diese im Kern ein bißchen weniger tief
waren als erwartet, dafür waren die Flügel ein bißchen zu breit. Mit
der Annahme eines weiteren turbulenten Geschwindigkeitsfeldes konnte
auch diese Diskrepanz beseitigt werden. Die Makro-Turbulenz kann
tatsächlich mit der Granulation identifiziert werden, da Spektren von
nur einem Granulum keine Makro-Turbulenz mehr benötigen.
Makro-Turbulenz: Ursache: optische dicke Turbulenzelemente.
Mikro-Turbulenz: Ursache: optische dünne Turbulenzelemente.
Für Hauptreihensterne fand Gray einen Zusammenhang zwischen der
Makro-Turbulenz < ζRT > und Tef f :
< ζRT >∼ 3.95 Tef f − 19.25 [km s−1 ]
g
M/M
=
; g = 2.74 104 cm s−1
g
R/R
III. Fourier-Analyse der Sternspektren
Die Fourier-Transformierte einer Funktion H(λ) ist h(f ), gegeben durch:
Z +∞
h(f ) =
H(λ)e2πiλf dλ
−∞
wenn λ ist in Å gegeben ist, so hat die Fourier-Transformierte h(f ) die
Einheit Å−1 . “Das Linienprofil wird durch eine Überlagerung von vielen
sinus (cosinus)-Funktionen unterschiedlicher Amplitude und Frequenz
wiedergegeben”.
Um das ursprüngliche Spektrum wieder zu erhalten durch:
Z +∞
H(λ) =
h(f )e2πiλf df
−∞
Zur Veranschaulichung: Je breiter die Linie ist, um so schmaler ist deren
Fourier-Transformierte.
Der große Vorteil der Fourier-Analyse der Spektrallinien ist, dass wir
die einzelnen Funktionen die das Linienprofil verändern nur im FourierRaum multipliziert müssen.
Beispiel: Sei I(λ) die instrumentelle Profil, G(λ) das rotationsverbreiterte Profil and F0 (λ) das intrinsische Linienprofil des Sterns, so ist die
Fourier-Transformierte des beoabchtetetn Linieprofils nur das Produkt
der Fourier-Transformierten (I(f ), G(f ), F0 (f )) dieser Funktionen:
D(f ) = I(f ) ∗ G(f ) ∗ F0 (f )
Mit der oben angegebenen Rücktransformation ließe sich zwar das beobachtete Linieprofil reproduzieren, es ist aber einfacher gleich im Fourierraum zu bleiben.
Auch das “Rauschen” der Fourier-Transformierten läßt sich leicht ableiten:
√
Sf = S λ ∆ λ N
wobei Sλ das Signal-zu-Rausch-Verhältnis ist, N die Anzahl der Datenpunkte im Linienprofil und ∆λ der Abstand zweier Datenpunkte [in Å].
Die Abbildung zeigt die Fourier-Transformierte der Fe II 4352 Linie von
α Aql. Die Dreiecke sind die beobachtetet Werte. Das instumentelle
Profil wurde bestimmt, fourier-transformiert und die Fourier-Transformierte des beobachteten Spektrum dadurch dividiert: Das Resultat ist die
oberen Kurve (schwarze Quadrate). Diese Kurve wurde dann modelliert.
Es ergab sich einem v sin i von 207 km s−1 .
IV. Die Granulation
Die Granulation wird durch die Konvektion hervorgerufen, ist aber nicht
die Konvektion, da wir die Granulation in der (radiativen) Photosphäre
beobachten. Die Granulation entsteht dadurch, dass die konevtiven
Zellen genug Impuls haben um in die konvektivstabile Schicht der Photosphäre “überzuschießen” (Overshoot-Schicht). Diese Overshoot-Schicht
hat ein Dicke von nur etwa 200 km. Die Granulation besteht aus heißen,
aufsteigenden Zellen (den Granulen) und kühlen absteigenden Regionen,
den intergranularen Räumen. Die Granulation ist als zellartiges Muster
zu erkennen.
IV.1 Die Typen der Granulation
Es gibt verschiedene Arten von Granulation:
i.) Die Granulation, mit Zellen von etwa 1000 km Durchmesser
ii.) Die Mesogranulation, mit Zellen von etwa 5-10000 km Durchmesser
iii.) Die Super-Granulation, mit Zellen von etwa 20-50000 km
Durchmesser
iv.) Die Giant Cells
VI.1.1 Die Granulation selber
Die Zahl der Granulen auf der Sonneoberfläche beträgt etwa ein Million.
Der Lebensdauer eines Granulums beträgt etwa 10 Minuten (35% fragmentieren, 60% tauchen ab, 4% verschmelzen). Vertikalen Geschwindigkeiten liegen bei 2 km/s (rms). Intensitätskontrast bei etwa 30%.
VI.1.2 Die Mesogranulation
Die Zahl der Meso-Granulen auf der Sonneoberfläche beträgt immer noch
100000. Die Lebensdauer eines Mesogranulums beträgt etwa 3 Stunden.
und die vertikalen Geschwindigkeiten liegen nur bei 60 m/s.
Die Existenz der Mesogranulation lässt sich nur sehr indirekt aus der
Beobachtung des horizontalen Strömungsmusters auf der Sonne ableiten
(Cork-Image).
VI.1.3 Die Supergranulation
Die Zahl der Supergranulen auf der Sonneoberfläche beträgt so etwa
1000. Die Lebensdauer eines Supergranulums beträgt etwa ein Tag. und
die vertikalen Geschwindigkeiten liegen nur bei 40 m/s.
Die Supergranulation lässt sich wieder aus der Beobachtung des horizontalen Strömungsmusters auf der Sonne ableiten, sie ist aber auch
als Zellenmuster bei Beobachtungen mit einem CaII Filter zu erkennen
(“chromospheric emission network”).
VI.1.4 Die Giant Cells
Die Giant Cells wurden durch die sehr genaue Analyse der Sonnenrotation entdeckt. Mit einem Durchmesser von 100000 km sind die Zellen
wirklich groß . Es gibt nur einige wenige dieser Zelle auf der Sonne. Die
Giant-Cells sind sehr schwierig nachzuweisen, da sie von der differentiellen Rotation überlagert sind.
VI.2 Woher kommen die Strukturen?
Wasserstoff ist in 2000 km Tiefe zu 50% ionisiert −− > Granulation
Helium I ist in 7000 km Tiefe zu 50% ionisiert −− > Mesogranulation
Helium II ist in 30000 km Tiefe zu 50% ionisiert −− > Supergranulation
Giant Cells : Tiefe der Konvektionsschicht.