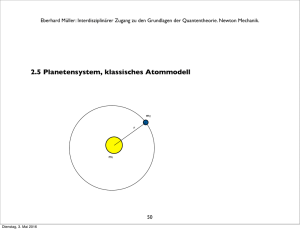
Theoretische Physik V Höhere Quantentheorie

Theoretische Physik V
Höhere Quantentheorie
Skritpum
o.Univ.-Prof. Urbaan M. Titulaer
Institut für Theoretische Physik
Universität Linz
SS 2009
Version vom 1. Oktober 2009
Vorwort
Dieses Skriptum basiert auf den Unterlagen zu Vorlesung ”Höhere Quantentheorie” von
o.Univ.-Prof. Urbaan M. Titulaer. Im Laufe der Zeit wurde dieses Skriptum um zwei Teilkapitel (”Verborgene Variablen und die Bell’sche Ungleichung” und ”Die Dichtefunktionalmethode”) erweitert, welche nun an den entsprechenden Stellen in diesen Text eingearbeitet
wurden. Sämtliche Abbildungen wurden neu erstellt und ersetzen die vorhandenen.
Der Inhalt ist weiterhin geistiges Eigentum des Urhebers der Originalversion, o.Univ.-Prof.
Urbaan M. Titulaer.
Die digitale Version wurde von Oskar Armbruster ([email protected]), Johannes Gall
([email protected]) und Philipp Kolmhofer ([email protected]) erstellt.
Dieses Skriptum wurde mit größter Sorgfalt erstellt und mehrfach auf Fehler kontrolliert.
Trotzdem kann nicht für die Fehlerfreiheit garantiert werden. Sollten Sie einen Fehler entdecken, so teilen Sie uns diesen bitte mit.
Linz, am 23. Juni 2009
Oskar Armbruster, Johannes Gall, Philipp Kolmhofer
Inhaltsverzeichnis
1 Zielsetzung und Inhaltsübersicht
4
2 Quantentheorie des Strahlungsfeldes
2.1 Die klassischen Feldgleichungen und die Feldoszillatoren . . . . . . . . . . .
2.1.1 Entwicklung nach Modenfunktionen . . . . . . . . . . . . . . . . . .
2.1.2 Das Vektorpotential; Ankoppelung an eine Stromdichte . . . . . . .
2.2 Quantisierung der Feldoszillatoren . . . . . . . . . . . . . . . . . . . . . . .
2.2.1 Der Hilbertraum des Strahlungsfeldes . . . . . . . . . . . . . . . . .
2.2.2 Superposition von Zuständen . . . . . . . . . . . . . . . . . . . . .
2.2.3 Einstein-Podolsky-Rosen Korrelationen . . . . . . . . . . . . . . . .
2.2.4 Verborgene Variablen und die Bell’sche Ungleichung . . . . . . . . .
2.2.5 Erwartungswerte von Feldoperatoren; Kohärente Zustände . . . . .
2.2.6 Regularisierung der Feldoperatoren . . . . . . . . . . . . . . . . . .
2.3 Das Strahlungsfeld in Wechselwirkung mit Atomen . . . . . . . . . . . . .
2.3.1 Wahl der störungstheoretischen Behandlung . . . . . . . . . . . . .
2.3.2 Die Matrixelemente der Störung; Die Dipolnäherung . . . . . . . .
2.3.3 Kurze Rekapitulation der zeitabhängigen Störungstheorie . . . . . .
2.3.4 Emission und Absorption von Strahlung . . . . . . . . . . . . . . .
2.3.5 Streuung von Photonen . . . . . . . . . . . . . . . . . . . . . . . . .
2.4 Das Atom im Strahlungsfeld: Spezielle Probleme . . . . . . . . . . . . . . .
2.4.1 Idealisierte Photodetektoren . . . . . . . . . . . . . . . . . . . . . .
2.4.2 Die Koinzidenz zweier Detektoren . . . . . . . . . . . . . . . . . . .
2.4.3 Ein Atom in einem Resonator . . . . . . . . . . . . . . . . . . . . .
2.4.4 Energieverschiebungen durch Ankopplung an die Vakuumfluktuationen (die Lamb-Verschiebung) . . . . . . . . . . . . . . . . . . . . .
2.4.5 Intermezzo: Die Selbstenergie freier Elektronen . . . . . . . . . . . .
6
6
8
9
10
12
13
16
18
19
22
23
24
25
26
27
29
33
33
35
37
3 Quantentheorie von Fermionfeldern
3.1 Hilbertraum und Feldoperatoren . . . . . . . . . . .
3.1.1 Feldoperatoren . . . . . . . . . . . . . . . .
3.1.2 Der Hamiltonoperator für Fermionfelder . .
3.2 Die Hartree-Fock-Näherung . . . . . . . . . . . . .
3.2.1 Die Bedeutung der Hartree-Fock Eigenwerte
48
48
50
51
52
57
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
40
43
3
INHALTSVERZEICHNIS
3.3
3.4
4 Die
4.1
4.2
4.3
4.4
4.5
3.2.2 Beispiel: Das Elektronengas . . . . . . . . . . . . . . .
3.2.3 Die Austauschenergie des Elektronengases . . . . . . .
3.2.4 Die Korrelationsfunktion (das Austauschloch) . . . . .
3.2.5 Die Dichtefunktionalmethode . . . . . . . . . . . . . .
Die Elektron-Phononwechselwirkung; Polaronen . . . . . . . .
3.3.1 Gitterschwingungen und ihre Quantisierung; Phononen
3.3.2 Die Elektron-Phonon-Wechselwirkung . . . . . . . . . .
Die BCS-Theorie der Supraleitung . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Dirac-Gleichung
Die ”Herleitung” der Dirac-Gleichung
Nichtrelativistische Näherungen . . .
Lösungen der freien Dirac-Gleichung
Die Löchertheorie . . . . . . . . . . .
Quantisierung des Diracfeldes . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
87
. 87
. 92
. 97
. 105
. 109
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
59
60
63
64
66
66
70
74
Kapitel 1
Zielsetzung und Inhaltsübersicht
In dieser Vorlesung werden wir einige Themen und Methoden behandeln, die über den Stoff
der Kursvorlesungen ”Quantenmechanik” und ”Thermodynamik und Statistische Physik”
hinausgehen, aber andererseits von genügend allgemeinem Interesse sind und in verschiedenen Teilbereichen der Physik ihre Anwendung finden. Es wird dabei ein gewisser Überlapp
mit den Vorlesungen ”Theoretische Atom- und Kernphysik” und ”Theoretische Festkörperphysik” auftreten, aber der Akzent wird in dieser Vorlesung eher auf der allgemeinen
Methodik als auf den spezifischen Anwendungen liegen. Andererseits werde ich versuchen,
bei jedem neu eingeführten Formalismus auch einige Anwendungen zu diskutieren; nur so
kann die Motivation zur Einführung des Formalismus einsichtig gemacht werden.
Das wichtigste Thema der Vorlesung ist die Beschreibung von Vielteilchensystemen,
insbesondere auch von solchen, in denen Teilchen erzeugt und vernichtet werden können.
Für solche Systeme reicht die in der Vorlesung Quantenmechanik verwendete Beschreibung
nicht aus; dort wurde die Zahl der Teilchen bei der Spezifizierung des Hilbertraumes (Zahl
der Freiheitsgrade sowie Festlegung des Symmetriecharakters bezüglich Vertauschung identischer Teilchen) (ein für allemal) festgelegt.
Als Einstieg in die Behandlung von Vielteilchensystemen behandeln wir in Kap. II die
Quantentheorie des Strahlungsfeldes. Aus der Elektrodynamik ist bekannt, dass das
Strahlungsfeld sich dynamisch verhält wie ein System harmonischer Oszillatoren, und es
liegt nahe, auf diesen Feldoszillatoren die Quantisierungsvorschrift für ”normale” Oszillatoren anzuwenden. Dies führt auf natürliche Weise zu einer für Bosonen angemessenen
Beschreibung; nach Einbeziehung der Wechselwirkung mit einem Atom können auch Absorption und (spontane und stimulierte) Emission von Strahlung auf recht natürliche Weise
erklärt werden. (Der für das Strahlungsfeld entwickelte Formalismus kann auch für sonstige
Oszillatoren verwendet werden; als Beispiel werden wir in Kap. III kurz die Beschreibung
von Gitterschwingungen diskutieren.) Aufgrund der unendlichen Zahl der Feldoszillatoren treten in der Theorie Divergenzen auf; wir werden an einigen Beispielen zeigen, wie
man diese, wenigstens formal, durch Renormierungsverfahren beseitigen kann.
In Kap. III zeigen wir, wie der Formalismus für die Behandlung von Systemen aus
vielen Fermionen modifiziert werden muss. Dies ist von Interesse für die Beschreibung
von Atom, Molekül und Festkörper. Als erstes diskutieren wir die Hartree-Fock-Näherung,
4
KAPITEL 1. ZIELSETZUNG UND INHALTSÜBERSICHT
5
und illustrieren sie am Beispiel des Elektronengases. Es erweist sich dabei als nützlich,
auch für die Elektronen einen Formalismus mit Erzeugungs- und Vernichtungsoperatoren einzuführen. Dieser Formalismus wird wohl etwas irreführend ”zweite Quantisierung”
genannt. Der so erhaltene Formalismus erweist sich als besonders geeignet für die Formulierung der BCS-Theorie der Supraleitung. Wir werden auch kurz auf die Herleitung der
in der BCS-Theorie auftretenden anziehenden Elektron-Elektron Wechselwirkung aus der
Elektron-Phonon Wechselwirkung eingehen.
In Kap. IV diskutieren wir die von Dirac vorgeschlagene relativistische Wellengleichung
für ein Teilchen mit Spin 12 . Die physikalische Interpretation dieser Gleichung weist einige
Schwierigkeiten auf, welche auf das Auftreten von Lösungen mit negativer Energie zurückzuführen sind. Diese Schwierigkeiten lassen sich weitgehend dadurch beseitigen, dass
man annimmt, dass sämtliche Zustände mit negativer Energie im energetisch niedrigsten
zugänglichen Zustand des Systems besetzt sind. Durch diese Annahme ist aber auch die
Dirac-Theorie nicht länger eine reine Ein-Teilchen-Theorie; eine Umformulierung in eine
Viel-Teilchen-Theorie erscheint angebracht, aber wir werden diese Umformulierung in dieser Vorlesung nicht explizit durchführen.
Literatur
Bisher habe ich kein Buch gefunden, in dem sämtliche Themen der Vorlesung behandelt
werden. Viele der Themenkreise werden behandelt in:
A. Messiah, Quantum Mechanics, Teil II.
J. J. Sakurai, Advanced Quantum Mechanics.
H. A. Bethe und R. W. Jackiw, Intermediate Quantum Mechanics.
W. Greiner, Theoretische Physik 4A: Quantentheorie, Spezielle Kapitel.
Insbesondere für Probleme der Festkörpertheorie:
C. Kittel, Quantum Theory of Solids.
J.M. Ziman, Electrons and Phonons.
Kapitel 2
Quantentheorie des Strahlungsfeldes
2.1
Die klassischen Feldgleichungen und die Feldoszillatoren
Ausgehend von den Maxwellgleichungen im freien Raum
∂B
= −c ∇×E
∂t
∇·B = 0
∂E
= c ∇×B
∂t
∇·E = 0
suchen wir zuerst nach speziellen Lösungen vom Typ
E(r, t) = e(r)q(t)
B(r, t) = b(r)p(t).
(1.1)
Substitution in die Maxwellgleichungen liefert
e(r)q̇(t) = c p(t) ∇×b(r);
b(r)ṗ(t) = −c q(t) ∇×e(r).
In beiden Gleichungen steht auf beiden Seiten jeweils ein Produkt einer reinen Ortsfunktion
und einer reinen Zeitfunktion. Gleichheit für alle r und t ist nur möglich, falls es zwei
Konstanten α und β gibt, so dass
q̇ = αp;
ṗ = −βq;
c ∇×b = αe;
c ∇×e = βb.
(1.2)
Das ineinander Substituieren dieser Gleichungen ergibt
p̈ = −ω 2 p
q̈ = −ω 2 q
ω 2 = αβ,
also die typischen Oszillatorgleichungen, sowie
∇×( ∇×b) =
ω2
α
∇×e = 2 b.
c
c
6
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
7
Aus letzterer Gleichung kann man über
∇×( ∇×b) = ∇( ∇·b) − ∇2 b
und ∇·b = 0, sowie die analogen Beziehungen für e, auf die Eigenwertgleichungen
∇2 b = −
ω2
b
c2
∇2 e = −
ω2
e
c2
schließen. Diese Gleichungen sind formal analog zur zeitunabhängigen Schrödingergleichung für ein freies Teilchen. Im unendlichen Raum sind die Lösungen ebene Wellen vom
Typ
eik (r) ≈ êi eikr ,
wobei êi ein Einheitsvektor ist mit êi ⊥ k. Die zugehörige Frequenz ist
ω = ck.
Der Wellenvektor k kann alle reellen Werte annehmen; bei jedem Wert von k gibt es zwei
linear unabhängige Polarisationsvektoren êi .
Weil das Arbeiten mit einem überabzählbaren Satz nicht konventionell normierbarer
Funktionen etwas unbequem ist, legt man oft periodische Randbedingungen auf einem
Kubus mit Kantenlänge L fest:
e(x + lx L, y + ly L, z + lz L) = e(x, y, z)
für alle ganze Zahlen lx , ly und lz . Dadurch werden die zulässigen Werte von k eingeschränkt
auf
k=
2π
(nx , ny , nz )
L
mit nx , ny und nz ganze Zahlen.
Für das Feld in einem Hohlraum mit spiegelnden Wänden sind die zulässigen Werte von ω
diskret (siehe Vorlesung Elektrodynamik). Dafür sind dann aber die sog. Modenfunktionen
en (r) und bn (r) von etwas komplizierterer Gestalt; sie können aber immer reell gewählt
werden. Auch für den Fall periodischer Randbedingungen kann man wegen der Entartung
zwischen k und −k, das Paar Modenfunktionen êi eikr und êi e−ikr durch êi sin kr und
êi cos kr ersetzen. So erhält man für alle Fälle einen Satz reeller Modenfunktionen, was
für die weitere formale Entwicklung einige Vorteile bietet. [Wir werden im weiteren die
Modenfunktionen mit einem einfachen Index k (für Wellenvektor und Polarisation!) durchnummerieren.] Am Schluss unserer Herleitung werden die für komplexe Modenfunktionen
erforderlichen Modifikationen ohne explizite Rechnung erwähnt werden.
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
8
Normierung:
Weil die Aufspaltung (1.1) nur bis auf Konstanten eindeutig ist, können wir für die Modenfunktionen eine im Prinzip beliebige Normierung wählen. Auch die Konstanten α und
β können unter Beibehaltung von αβ = ω 2 frei gewählt werden; die Wahl α = β = ω liegt
nahe. Mit dieser Wahl gilt dann aufgrund von (1.2):
Z
Z
c2
( ∇×ek ) ( ∇×ek ) dr
bk (r)bk (r)dr = 2
ω V
V
(1.3)
Z
c2
= 2
ek ( ∇× ( ∇×ek )) dr + Oberflächenterm.
ω V
Dabei bezeichnet V das Periodizitäts- oder Hohlraumvolumen. (Das auf den ersten Blick
anomale Vorzeichen des partiell integrierten Terms kann durch Ausschreiben in Komponenten überprüft werden; siehe Skriptum Elektrodynamik.)
Der Oberflächenterm ist proportional zu
I
I
2
d O (n̂×ek )bk = d2 O n̂ (ek ×bk ) ,
also proportional zum Oberflächenintegral der Normalkomponente des Poyntingvektors,
d.h. der Energiestromdichte. Für reelle Modenfunktionen verschwindet diese Größe; hätten
wir komplexe Modenfunktionen gewählt, so hätten sich aufgrund der periodischen Randbedingungen die Beiträge der Kantenflächen der Kuben jeweils paarweise kompensiert.
Aus (1.3) schließt man jetzt nach Einsetzen der Eigenwertgleichung
Z
Z
bk (r)bk (r)dr = ek (r)ek (r)dr
Weiters sind natürlich Modenfunktionen mit verschiedenen Indizes orthogonal zueinander.
Wir wählen jetzt als Normierungsbedingung
Z
e∗k (r)ek0 (r)dr = 4πωk δkk0 ,
(wobei die Verallgemeinerung auf komplexe Modenfunktionen miteingeschlossen wurde).
Für den Fall eines kontinuierlichen Modenindex wählt man auf analoge Weise
Z
e∗ki (r)ek0 j (r)dr = 4 πωk δ 3 (k − k0 )δij .
2.1.1
Entwicklung nach Modenfunktionen
Aus der Vollständigkeit der Modenfunktionen ek (r) oder bk (r) folgt, dass man jedes transversale Feld nach ihnen entwickeln kann:
Z
X
1
E ek dr
E(r, t) =
ek (r)qk (t)
mit qk (t) =
4πω
k
k
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
B(r, t) =
X
bk (r)pk (t)
k
1
mit pk (t) =
4πωk
9
Z
B bk dr
Einsetzen dieser Entwicklungen in den Ausdruck für die Feldenergie liefert
Z
1
W (t) =
dr |E(r, t)|2 + |B(r, t)|2
8π
Z
Z
1 X
=
qk qk 0
dr ek ek0 + pk pk0
dr bk bk0
8π kk0
V
V
1X 2
=
ωk pk (t) + qk2 (t) .
2 k
Wenn man diesen Ausdruck als Hamiltonfunktion auffasst:
W (t) = H({pk , qk }),
so erhält man als die Hamilton’schen Bewegungsgleichungen
ṗk = −
∂H
= −ωk qk
∂qk
q̇k =
∂H
= ωk pk ,
∂pk
also genau die vorher aus dem Separationsansatz erhaltenen Ausdrücke.
2.1.2
Das Vektorpotential; Ankoppelung an eine Stromdichte
Wie aus der Elektrodynamik bekannt ist, können die Felder E und B mittels
B = ∇×A
E=−
1 ∂A
− ∇φ
c ∂t
in einem Vektorpotential A und einem skalaren Potential φ ausgedrückt werden. Die oben
angegebenen allgemeinen Ausdrücke für rein transversale Felder E und B können hergeleitet werden aus
X c
φ(r, t) = 0
A(r, t) =
pk (t)ek (r).
ω
k
k
Diese Wahl ist nicht eindeutig; sie entspricht der Coulomb-Eichung
∇·A = 0;
diese Eichung ist für den Übergang zur Quantentheorie die bequemste; sie hat aber den
Nachteil, dass sie nicht relativistisch kovariant ist.
In Anwesenheit von Ladungen und Strömen werden zwei der Maxwellgleichungen abgeändert in
∂E
= c ∇×B − 4πj
∂t
∇·E = 4πρ.
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
10
Aus der ersten Gleichung erhält man durch skalare Multiplikation mit ek (r), Einsetzen der
Modenentwicklungen für E und B, Einsetzen von ∇×bk = ωck ek , und Integration über r:
Z
1
dr j(r, t)ek (r).
q̇k = ωk pk + gk (t)
mit gk (t) = −
ωk
Die Feldoszillatoren führen jetzt also erzwungene Schwingungen aus. Die obige Gleichung kann auch aus dem Hamilton’schen Formalismus erhalten werden; dazu nimmt man
in H einen Zusatzterm
Z
X
1
H1 = −
dr j(r, t)A(r, t) =
pk (t)gk (t)
c
k
auf. Für den longitudinalen Anteil von E erhält man keine Bewegungsgleichung, sondern
lediglich die Bestimmungsgleichung ∇·Ek = 4πρ mit der Lösung
Z
ρ(r0 , t)
Ek = −∇φ
φ(r, t) = dr0
|r − r0 |
Im Hamilton’schen Formalismus spielen also, wenigstens in der Coulomb-Eichung, die Größen A und φ recht unterschiedliche Rollen: A ist eine Linearkombination von Impulsen von
Feldoszillatoren und wird in der Quantentheorie zu einem Operator; φ ist ein Integral über
die Ladungsverteilung und hat mit den Feldoszillatoren nichts zu tun; es bleibt auch in
der Quantentheorie eine reine Zahlenfunktion, wenigstens bezüglich der Freiheitsgrade des
elektromagnetischen Feldes. (Die Ladungsverteilung ρ kann, wie wir später sehen werden,
unter Umständen selbst Operatorcharakter haben; wenn φ(r, t) in einer Schrödingergleichung vorkommt, muss weiters r als der Ortsoperator des beschriebenen Teilchens interpretiert werden. Dies sind übrigens ”Komplikationen” die bei der Interpretation von A(r, t)
genauso auftreten.)
2.2
Quantisierung der Feldoszillatoren
Wie zuerst von Dirac vorgeschlagen wurde, kann man aus der im vorherigen Abschnitt
behandelten Hamilton’schen Theorie des Strahlungsfeldes dadurch eine Quantentheorie
erhalten, dass man die Koordinaten qk und die Impulse pk der Feldoszillatoren ersetzt
durch Operatoren Qk und Pk , die die Vertauschungsrelationen
[Pk , Qk0 ] =
~
δkk0
i
erfüllen. Man erhält so für die Hamiltonoperatoren
H=
1X 2
ωk Pk + Q2k
2 k
H1 =
X
k
Pk gk (t).
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
11
Zur Diskussion des Spektrums von H führen wir, wie für ”normale” Oszillatoren, Leiteroperatoren ein:
1
a†k = √ (Qk − iPk )
2~
r
~
Pk = −i
(ak − a†k ).
2
1
ak = √ (Qk + iPk )
2~
r
~
(ak + a†k )
Qk =
2
Hieraus folgen die Vertauschungsrelationen
h
i
†
ak , ak0 = δkk0
und der Ausdruck für den freien Hamiltonoperator
X
1
†
H=
~ωk ak ak +
.
2
k
Die Eigenwerte dieses Operators sind, wie für ”normale” Oszillatoren,
X
1
E{nk } =
~ωk nk +
2
k
mitP
willkürlichen nk ≥ 0. Dies sieht auf den ersten Blick wegen der Divergenz der Summe
1
~ k ωk ziemlich beunruhigend aus. Weil aber nur Energieunterschiede physikalisch
2
relevant sind, können wir den divergenten Term in H genausogut weglassen und schreiben
X
X
~ωk a†k ak
~ωk nk .
H=
E{nk } =
k
k
Das heißt aber nicht, dass die sogenannte ”Nullpunktsenergie” physikalisch völlig ohne
Bedeutung ist; sie spielt eine Rolle, wenn wir Änderungen der Randbedingungen
vornehmen. Dazu betrachten wir z.B. einen kubischen Hohlraum, der durch eine bewegliche
Metallplatte in zwei Teile geteilt ist.
a
L−a
Die Eigenschwingungen des geteilten Hohlraumes hängen von der Position der Platte
ab. Die damit zusammenhängende Änderung der Nullpunktsenergie führt zu einer Kraft
auf die Platte, die von Casimir berechnet werden konnte. Seine Ergebnisse konnten später
12
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
experimentell genau bestätigt werden. Dies ist ein typisches Phänomen für die Quantentheorie von Systemen mit unendlich vielen Freiheitsgraden: In einer solchen Theorie treten
oft formal divergente Ausdrücke auf, die man zuerst wegen ihrer prinzipiellen Nichtbeobachtbarkeit außer Acht lassen kann. Bei genauerer Betrachtung ergibt aber die Änderung
eines solchen Ausdrucks bei Änderung irgendeines Systemparameters (eine Größe, die nur
mit Hilfe recht abenteuerlicher mathematischer Verfahren überhaupt berechnet werden
kann) einen interessanten beobachtbaren physikalischen Effekt. Die quantitative Vorhersage, erhalten durch solche abenteuerliche Manipulationen mit divergenten Größen, stimmt
dann typischerweise sehr genau mit den experimentellen Beobachtungen überein.
2.2.1
Der Hilbertraum des Strahlungsfeldes
Bisher haben wir zwar die Operatoren H, B und E eingeführt, aber noch nicht den Hilbertraum spezifiziert, in dem sie arbeiten. Die Analogie mit der herkömmlichen Quantenmechanik legt es aber nahe, die Eigenzustände von H als Basiszustände (Basis-Eigenvektoren)
des Hilbertraumes zu verwenden. Eine zentrale Rolle spielt der Vakuumzustand |{0} ,
definiert durch
ak |{0} = 0
für alle k,
der dem Grundzustand von H entspricht. Durch mehrfaches Anwenden von Erzeugungsoperatoren erhält man die Zustände
nk 

†
Y ak
 |{0}
√
(2.1)
|{nk } = 
n
!
k
k
(mit nur endlich vielen nk 6= 0!), die den Energieeigenwerten
X
E{nk } =
~ωk nk
k
entsprechen. Als neue Sprachregelung führen wir ein, dass sich im Strahlungsfeld im Zustand |{nk } jeweils nk Photonen der Sorte k befinden. Dabei ist die ”Sorte” durch die
Modenfunktion spezifiziert. Der von den Basisvektoren aufgespannte Raum (2.1) heißt
Fockraum. Er besteht aus allen Linearkombinationen
X
X
|φ =
c{nk } |{nk }
mit
|c{nk } |2 = 1.
{nk }
{nk }
Dabei läuft die Summation über alle Reihen ganzer Zahlen nk , bei denen
ist.
P
k
nk endlich
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
2.2.2
13
Superposition von Zuständen
Aus der Definition (2.1) und den Vertauschungsrelationen
zwischen ak und a†k kann man
leicht herleiten, dass der Zustand |{nk } zugleich ein Eigenzustand des Operators
X †
N=
ak ak
k
mit dem Eigenwert
X
n{nk } =
nk
k
ist. Der Operator
N heißt Photonenzahloperator; N hat wesentlich mehr Eigenzustände
als die |{nk } . So ist z. B. auch der Zustand
|α, β = αa†k + βa†l |{0}
|α|2 + |β|2 = 1
ein Eigenzustand von N mit dem Eigenwert 1. Er entspricht einem Feld, in dem ein einzelnes Photon in irgendeiner (gleich genauer zu bestimmenden) linearen Superposition der
Moden ek (r) und el (r) angeregt ist. Die Zeitentwicklung des obigen Zustandes ist
−iωk t †
−iωl t †
ak + βe
al |{0} ;
|α, β t = αe
der Zustand ist also nur für den Spezialfall ωk = ωl ein stationärer Zustand. Der obige
Zustand beschreibt also eine ganz andere Situation als der Zustand
|1k , 1l = a†k a†l |{0} .
Letzterer ist immer stationär; er entspricht der Situation, in der das Feld genau zwei
Photonen enthält, eins der Sorte k und eins der Sorte l.
Um die physikalische Bedeutung von Zuständen des Typs |α, β etwas genauer zu bestimmen, betrachten wir den Operator des elektrischen Feldes, der geschrieben werden
kann als
r
h
i
~X
ek (r) ak (t) + a†k (t) .
(2.2)
E(r, t) =
2 k
Eine ähnliche Darstellung sollte es natürlich für jede Wahl eines vollständigen Systems
{ek (r)} geben. Wir betrachten insbesondere eine unitäre Basistransformation Ukl , die nur
energetisch entartete Eigenfunktionen miteinander vermischt:
Ukl = 0
falls ωk 6= ωl .
(2.3)
Man überprüft leicht, dass man mit Hilfe der Transformationen
X
X
X
ẽk =
Ukl el
ãk =
Ukl∗ al
ã†k =
Ukl a†l
l
l
l
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
die Darstellung
r
E(r, t) =
14
i
~ Xh
†
∗
ẽk (r)ãk (t) + ẽk (r)ãk (t)
2 k
erreicht. Für den Hamiltonoperator erhält man
X
H=~
ωk ã†k ãk ,
k
und es liegt nahe, ã†k als Erzeuger eines Photons mit der Modenfunktion ẽk zu interpretieren. (Für die Wahl von ẽk anstelle von ẽ∗k werden wir gleich ein Argument geben.)
Beispiel 1:
e1 ∼ êx cos kz
ẽ1,2 ∼ êx e±ikz
e2 ∼ êx sin kz
Die entsprechenden ã†1,2 erzeugen Photonen mit den Wellenvektoren +kêz bzw −kêz . Dieses
Beispiel gestattet es, die obige Mehrdeutigkeit zwischen ẽk und ẽ∗k zu entscheiden. Falls wir
jedem Photon mit Wellenvektor k einen Impuls ~k zuordnen, so liegt es nahe, als Operator
für den Gesamtimpuls P des Feldes den Ausdruck
X †
k ak,i ak,i
P=~
k,i
anzusetzen. Nur für die oben festgelegte Identifikation stimmt dies mit dem Ausdruck
Z
1
P=
dr E(r)×B(r)
4πc V
aus der Maxwelltheorie überein.
Beispiel 2:
e1 ∼ êx eikz
e2 ∼ êy eikz
Linearkombinationen von a†1 und a†2 mit reellen Koeffizienten erzeugen linear polarisierte
Photonen mit einem Polarisationsvektor in der x-y-Ebene. Für ein komplexes Verhältnis
α/β erhält man elliptische Polarisation; insbesondere für α/β = ±i links oder rechts zirkular polarisierte Photonen.
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
15
Wellenpakete
Wenn man im obigen Formalismus die Nebenbedingung (2.3) fallen lässt, so geht die Diagonalform von H in der Transformation verloren. Die ã†k erzeugen dann Photonen, die
keinen stationären Zuständen des Strahlungsfeldes entsprechen, sondern Wellenpaketen.
Bei der Definition der Amplitude eines solchen Wellenpaketes tritt allerdings eine Komplikation auf. Das Betragsquadrat der Größe
X
ẽl (r) =
Ulk ek (r)
k
hängt mit der Energiedichte zusammen. Die entsprechende Größe für die Teilchendichte
setzen wir an als
X 1
√
Ulk ek (r).
f̃l (r) =
4πωk
k
Aus der Normierung der ek folgt, dass |f̃l |2 immer auf eins normiert ist; sein Betragsquadrat
kann also als Aufenthaltswahrscheinlichkeit des Photons interpretiert werden. Diese
Interpretation wird unterstützt vom folgenden
Lemma: Seien
X
b†1 =
U1k a†k
k
b†2 =
X
U2k a†k
k
und entsprechend
fi (r) =
X
k
1
√
Uik ek (r)
4πωk
so gilt
Z
h
i X
†
∗
b1 , b2 =
U1k U2k =
dr f1∗ (r)f2 (r).
k
V
Insbesondere verschwindet also der Kommutator, falls die Funktionen f1 (r) und f2 (r) nicht
überlappen: Man ”kann kein Photon vernichten an einem Punkt, wo das Photon sich nicht
aufhält”.
Die obige Betrachtung ist recht plausibel, aber genau gesehen wurde die intuitive Bedeutung der Bezeichnung ”Erzeuger” oder ”Vernichter” etwas überstrapaziert! In einer vernünftigen Theorie sollte man eigentlich überhaupt nicht von ”Aufenthaltswahrscheinlichkeiten” für Photonen reden, sondern nur von Nachweiswahrscheinlichkeiten für ganz bestimmte Detektoren (mit ggf. frequenzabhängigen Empfindlichkeiten). Weiters sollte man
im Auge behalten, dass die Wellenausbreitung des Lichtes im Vakuum nicht-dispersiv
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
16
ist. Das Auseinanderlaufen von Wellenpaketen ist also lediglich auf Unschärfe in der Richtung von k zurückzuführen. Für ein zur Zeit t = 0 scharf lokalisiertes Wellenpaket sind
also auch für spätere Zeiten ẽl (r, t) und f̃l (r, t) in den gleichen Teilen des Raumes konzentriert. (Die zeitabhängigen Amplituden erhält man dadurch, dass man in der Entwicklung
nach den stationären Modenfunktionen jedem ek (r) einen Zeitfaktor e−iωk t gibt.) Schließlich enthalten die meisten in der Praxis auftretenden Wellenpakete nur Komponenten aus
einem relativ schmalen k-Bereich (d.h. sie haben eine relativ wohldefinierte Energie). Auch
deshalb ist der Unterschied zwischen ẽl und f̃l für die Praxis eher unwichtig.
2.2.3
Einstein-Podolsky-Rosen Korrelationen
Ein spezieller Typ von Zuständen mit typisch quantenmechanischen Eigenschaften tritt z.B.
beim Zerfall eines ruhenden Positronium-Atoms aus dem Grundzustand in zwei γ-Quanten
auf. Aufgrund der Erhaltung von Impuls und Drehimpuls weiß man, dass der gebildete
Zwei-Photonzustand einen Gesamtimpuls und einen Gesamtdrehimpuls gleich Null haben
muss. Impuls und Drehimpuls der einzelnen Photonen sind aber völlig unbestimmt. Ein
Zustand der diese Anforderungen erfüllt ist
h
i
X
g(|k|) a†k,+ a†−k,− + a†k,− a†−k,+ |{0} ;
|pos ∼
k
hier bezeichnen die a†k,± die Erzeuger für Photonen mit Impuls k und positive, bzw negative
zirkulare Polarisation. Die Funktion g(k) ist so gewählt, dass
f (r) =
X
k
√
1
g(k)eikr
4πωk
in der Nähe des Ursprungs lokalisiert ist. Die entsprechende Amplitude zur Zeit t ist dann
auf einer Kugelschale mit dem Radius R = ct lokalisiert. Für genügend großes R in Richtung (θ, φ) tragen zur Amplitude in R nur Partialwellen
mit k in Richtung (θ, φ) bei. Ein
Detektor in (R, θ, φ) spricht also im Zustand |pos nur auf
Photonen mit k in Richtung
(θ, φ) an. Wie man leicht nachprüft, hat der Zustand |pos die Eigenschaft
aki a−k0 j |pos = 0
falls k 6= −k0 .
Mit der ”intuitiven” Deutung der Vernichter heißt dies für den Fall, dass die Kugel mit
Radius R mit vielen Detektoren besetzt ist:
Wenn ich im Punkt (R, θ, φ) ein Photon aus dem Zustand |pos detektiere, so
weiß ich damit auch, dass zu etwa der gleichen Zeit nur der Detektor im Punkt
(R, π − θ, 2π − φ) ein Photon detektieren kann; alle anderen Detektoren sehen
mit Sicherheit nichts.
Ich erhalte also Information über Ereignisse, die in der Relativitätstheorie als zu mir raumartig bezeichnet werden. Dieser Aspekt der Quantentheorie, der zuerst von Einstein, in
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
17
Zusammenarbeit mit Podolsky und Rosen bemerkt wurde, war für ihn Anlass, die Quantentheorie trotz ihrer Erfolge abzulehnen oder zumindest als eine unvollständige Theorie
zu bezeichnen.
Auf den ersten Blick erscheint ein Ausweg möglich, wobei man den Photonen ”verborgene Parameter” zuschreibt, die von der Quantentheorie nicht erfasst werden. Das obige Experiment wäre dann vergleichbar mit einem Versuch, in dem ich zwei Hälften einer Banknote
an zwei weit auseinander wohnende Freunde mit perfekt synchronisierter Postzustellung zuschicke; in dem Fall würde sich niemand über Informationen mit Überlichtgeschwindigkeit
bezüglich gelesener Seriennummern usw. aufregen. Erklärungsversuche dieser Art scheitern
aber, wenn man auch die Polarisationsfreiheitsgrade mit ins Spiel bringt. Wenn man sich
auf die Komponenten
mit k in der z-Richtung beschränkt, so überprüft man leicht, dass
man für |pos die zwei äquivalenten Darstellungen
† †
†
†
|pos ∼ ak,+ a−k,− + ak,− a−k,+ |{0}
und |pos ∼ a†k,x a†−k,x + a†k,y a†−k,y |{0}
angeben kann. (Der Beweis benützt die oben in Beispiel 2 gegebenen Beziehungen.) Mit einem Argument wie oben schließt man, dass aus Information über entweder die lineare oder
die zirkulare Polarisation des einen Photons sofortige Information über die entsprechende
Polarisation des anderen Photons folgt. Weil ich weiters mit der Entscheidung, ob ich lineare oder zirkulare Filter vor meine Detektoren setze, warten kann bis die Photonen schon
emittiert sind, müssen die Photonen in einer Verborgenen-Parameter-Theorie also genaue
Information sowohl über ihre zirkulare als auch über ihre lineare Polarisation mit sich führen. Da dies genaue Kenntnisse über die Werte zweier nicht-vertauschenden Operatoren [für
etwas explizitere Angabe dieser Operatoren siehe Kap. II des Skriptums Quantenmechanik]
bedeuten würde, impliziert eine solche Vorstellung eine Verletzung der Heisenberg’schen
Unschärferelationen; letztere sind aber in Experimenten vom Stern-Gerlach Typ vielfach
bestätigt worden!
Bemerkung 1:
Bei der praktischen Durchführung von Experimenten, in denen die Filter erst nach der
Emission der Photonen eingestellt werden (delayed choice experiments), muss vom obigen
Schema etwas abgewichen werden; die Photonen müssen durch Spiegel umgeleitet und
”aufgehalten” werden, damit eine synchrone Einstellung rechtzeitig stattfinden kann.
Bemerkung 2:
Ein quantitativer Test von Theorien mit verborgenem Parameter kann mittels der sog.
Bell’schen Ungleichungen erfolgen. Dies sind Ungleichungen über Koinzidenzraten zwischen Photonen-Detektoren mit verschieden geneigten Polarisationsfiltern; sie sind erfüllt
in Theorien mit verborgenen Parametern (und
ohne instantane Wechselwirkungen), aber
verletzt für Quantenzustände vom Typ |pos . Experimente von Clauser und Shimony, und
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
18
später von Aspect, zeigten klare Verletzungen der Bell’schen Ungleichungen, und widerlegten damit klar die ”natürliche” Theorie mit verborgenen Parametern.
2.2.4
Verborgene Variablen und die Bell’sche Ungleichung
Wir betrachten für die Einstein-Podolsky-Rosen-Anordnung den Operator A+ (θ), der die
Werte +1 bzw. −1 annimmt, falls das Photon mit Impuls +~k einen unter dem Winkel
θ zur x-Achse geneigten Polarisationsfilter passiert, bzw. nicht passiert. Ähnlich definiert
man den Operator A− (θ) für das Photon mit dem Impuls −~k. Die Korrelation P(θ1 , θ2 )
ist definiert als Erwartungswert des Produktes dieser Operatoren
P(θ1 , θ2 ) = hA+ (θ1 )A− (θ2 )i .
Die Quantenmechanik macht für P(θ1 , θ2 ) die Vorhersage
P(θ1 , θ2 ) = cos [2 (θ1 − θ2 )] .
(2.4)
In einer Theorie mit verborgenen Variablen macht man die Annahme, dass das Ergebnis
der Messung sämtlicher Operatoren A± (θ) festgelegt ist durch einen ”verborgenen Parameter” λ, der bei der Präparation des Systems gemäß einer Wahrscheinlichkeitsverteilung
ρ(λ) gesetzt wird. (Der Wertebereich von λ kann dabei willkürlich sein.) Es existieren also
Funktionen A± (θ; λ) die die Werte ±1 annehmen können, und es gilt
Z
P(θ1 , θ2 ) = dλ ρ(λ)A+ (θ1 ; λ) A− (θ2 ; λ).
Aus dem experimentellen Ergebnis P(θ, θ) = 1 folgt (mindestens für fast alle λ)
A+ (θ; λ) = A− (θ; λ),
und daher werden wir weiters die Indizes ± weglassen. Wir betrachten jetzt
Z
P(θ0 , θ1 ) − P(θ0 , θ2 ) = dλ ρ(λ) [A(θ0 ; λ)A(θ1 ; λ) − A(θ0 ; λ)A(θ2 ; λ)]
Z
dλ ρ(λ)A(θ0 ; λ)A(θ1 ; λ) [1 − A(θ1 ; λ)A(θ2 ; λ)] ,
wobei wir die Identität A2 (θ; λ) = 1 ausgenutzt haben. Der Ausdruck in den eckigen
Klammern ist positiv semidefinit; es gilt also die Ungleichung
Z
|P(θ0 , θ1 ) − P(θ0 , θ2 )| 6 dλ ρ(λ) [1 − A(θ1 ; λ)A(θ2 ; λ)] ,
oder
|P(θ0 , θ1 ) − P(θ0 , θ2 )| 6 1 − P(θ1 , θ2 ).
(2.5)
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
19
Dies ist die Bell’sche Ungleichung. Sie ist mit der (experimentell bestätigten) Vorhersage
(2.4) der Quantenmechanik unverträglich. Dazu betrachtet man z.B. die Umgebung des
Punktes θ1 = θ2 . Die linke Seite ist linear in |θ1 − θ2 |, falls man θ0 nicht so wählt, dass die
Ableitung von P nach θ0 verschwindet. Die rechte Seite dagegen ist quadratisch in θ1 − θ2
für den (experimentell bestätigten) Ausdruck (2.4); es gibt also sicher einen Bereich, wo
die Ungleichung (2.5) verletzt ist!
Unser Schluss ist: Eine Theorie mit verborgenen Zuständen kann die Ergebnisse der
Quantenmechanik für EPR-Zustände nie voll reproduzieren. Im Experiment wählt man
Werte von θ0 , θ1 und θ2 für die die Verletzung der Ungleichung möglichst groß ist, und auf
jeden Fall größer als der experimentelle Messfehler.
2.2.5
Erwartungswerte von Feldoperatoren; Kohärente Zustände
Da die Feldoperatoren E(r, t) und B(r, t)in den ak und a†k linear sind, verschwinden ihre
Erwartungswerte in den Zuständen |{nk } :
{nk }|E(r, t)|{nk } = {nk }|B(r, t)|{nk } = 0
Zustände mit nicht-verschwindenden
Erwartungswerten von E und B müssen Linearkombi
nationen von |{nk } mit unterschiedlichen Besetzungszahlen sein. Die wichtigsten Beispiele solcher Zustände sind die kohärenten Zustände. Diese erhält man auf natürliche Weise
durch Betrachtung des Hamiltonoperators für das Strahlungsfeld in Wechselwirkung mit
einer klassischen Stromdichte j(r, t). Wie im vorherigen Abschnitt gezeigt wurde, gilt:
r
X
~ X
†
ak − a†k gk (t).
~ωk ak ak − i
H(t) =
2 k
k
Die Heisenberg’schen Bewegungsgleichungen für die ak (t) lauten
i
ih
d
ak (t) =
Ĥ(t), ak (t) ,
dt
~
wobei Ĥ(t) den Hamiltonoperator im Heisenbergbild (d.h. mit zeitabhängigen ak und a†k
darstellt. Der obige Ausdruck liefert
d
1
ak (t) = −iωk ak (t) + √ gk (t)
dt
2~
oder
d
1
ak (t)eiωk t = √ eiωk t gk (t).
dt
2~
Die Lösung ist
ak (t)e
iωk t
Z t
1
0
dt0 eiωk t gk (t0 )
= ak + √
2~ 0
= ak + αk (t),
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
20
oder
(2.6)
ak (t) = [ak + αk (t)] e−iωk t
und, auf völlig analoge Weise
h
i
a†k (t) = a†k + αk∗ (t) eiωk t .
Jetzt nehmen wir zusätzlich an, dass die Stromdichte j(r, t), und damit gk (t), für t < 0
verschwindet. Weiters soll das System für t = 0 im Vakuumzustand |{0} sein. Damit
ist der Zustand im Heisenbergbild also auch auf |{0} festgelegt. Den Schrödingerzustand
bezeichnen wir mit |{0}; t . Aus der Invarianz sämtlicher Matrixelemente für
den Übergang
zwischen Schrödinger- und Heisenbergbild erhält man für willkürliches |ψ
ψ|ak (t)|{0} = ψ; t|ak |{0}; t .
Andererseits folgt mit Hilfe von (2.6)
ψ|ak (t)|{0} = e−iωk t αk (t) ψ|{0}
= e−iωk t αk (t) ψ; t|{0}; t .
Aus der Gleichheit der beiden Ausdrücke für willkürliches |ψ , also auch für willkürliches
|ψ; t , folgt
ak |{0}; t = αk (t)e−iωk t |{0}; t .
Der Zustand |{0}; t ist also ein Eigenzustand sämtlicher {ak } mit Eigenwerten αk (t)e−iωk t .
Solche Eigenzustände für normale Oszillatoren haben wir im Skriptum
Quantenmechanik
diskutiert. Sie heißen kohärente Zustände und werden mit |α bezeichnet. Der Zusammenhang mit den Energieeigenzuständen ist
X αn 1
2
√ |n .
|α = e− 2 |α|
n!
n
Insbesondere gilt in diesem Zustand eine Poissonverteilung der Zahl der Energiequanten:
2n
2 |α|
| n|α |2 = e−|α|
.
n!
Die Verallgemeinerung für das Strahlungsfeld ist
"
#
#
"
X Y (αk )nk
1X
√
|{αk } = exp −
|αk |2
|{nk } .
2 k
nk !
k
{nk }
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
21
−iωk t
Der Zustand |{0}; t ist also, bis auf einen Phasenfaktor,
mit
dem
Zustand
|{α
(t)e
k
identisch. Insbesondere gibt es im Zustand |{0}; t nichtverschwindende Erwartungswerte
für E und B:
{0}; t|E(r, t)|{0}; t = Re{E(r, t)}
mit
E(r, t) =
√
2~
X
ek (r)αk (t)e−iωk t .
k
Dieser Erwartungswert ist genau die Lösung des entsprechenden klassischen Problems.
Die kohärenten Zustände eines Oszillators haben die zusätzliche Eigenschaft, dass die
Schwankungen von Energie und Impuls in ihnen genauso groß sind wie im Grundzustand.
Auch diese Eigenschaft lässt sich auf das Strahlungsfeld übertragen. Allerdings erhält man
für die Schwankungen im Grundzustand einen unendlichen Beitrag. Bei der Ausarbeitung
von
X
~
ek (r)ek0 (r) ak + a†k ak0 + a†k0 |{0}
{0}| |E(r)|2 |{0} = {0}|
2
kk0
liefern nur die Terme mit
{0}|ak a†k0 |{0} = δkk0
einen Beitrag; alle sonstigen Terme verschwinden wegen
ak |{0} = {0}|a†k = 0.
Die nichtverschwindenden Terme sind alle aber etwa von der Größe ωk V −1 und führen zu
einer Divergenz. Der Operator |E(r)|2 ist also nicht wohldefiniert. Aus schlechtdefinierten
Operatoren dieser Art kann man wieder wohldefinierte machen durch Subtraktion des
divergenten Anteils, also hier des Vakuumerwartungswertes. Für einen Operator A definiert
man den nichtdivergenten Anteil : A : symbolisch als
: A : = A − {0}|A|{0} .
Eine etwas präzisere Vorschrift ist:
a) Schreibe A als ein Polynom in den {ak } und {a†k0 }
b) Ändere in jedem Term die Reihenfolge der Faktoren so, dass alle ak rechts von allen
a†k0 , stehen.
Durch diesen letzten Schritt ist das Verschwinden des Vakuumerwartungswertes gesichert.
Der Operator : A : heißt die normalgeordnete Version von A. Als Beispiel betrachten wir
h
i
~X
ek (r)ek0 (r) ak ak0 + a†k a†k0 + a†k ak0 + a†k0 ak .
: |E(r)|2 : =
2 kk0
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
22
Es lässt sich leicht zeigen, dass gilt
2
{αk }| : |E(r)|2 : |{αk } = {αk }| E(r) |{αk } ,
also das Feld E hat im Zustand |{αk } keine größeren Schwankungen als im Vakuumzustand. Dasselbe lässt sich für das B-Feld auf gänzlich analoge Weise zeigen. Die Zustände
|{αk } sind also so klassisch wie in der Quantentheorie nur möglich.
2.2.6
Regularisierung der Feldoperatoren
Die oben aufgetretenen Schwierigkeiten (Divergenzen des Schwankungsquadrats) können
darauf zurückgeführt werden, dass wir uns wieder etwas zu weit von der physikalischen
Realität entfernt haben. In der Praxis misst man nie das Feld an einem scharfen Punkt,
sondern höchstens den Mittelwert des Feldes über ein Gebiet der Größe z.B. eines Licht
absorbierenden oder stimuliert emittierenden Atoms. Mathematisch kann man dies darstellen durch eine Verschmierungsfunktion φ(r − r0 ) und daran anschließend die sog.
regularisierten Operatoren
Z
Eφ (r) = dr0 φ(r − r0 )E(r0 )
einführen, wobei φ(r) eine glatte, positive Funktion mit beschränkter Reichweite ist, die
im übrigen ziemlich frei gewählt werden kann. Für das Schwankungsquadrat dieser Größe
im Vakuum erhält man
Z
2
X
~ X
0
0
0
2
dr φ(r − r )ek (r ) ≡
|φ̃k |2 .
{0}| |Eφ (r)| |{0} =
2 k
k
Da φ glatt ist, nehmen die Entwicklungskoeffizienten φ̃k , die im wesentlichen Fourierkomponenten sind, mit zunehmendem k sehr rasch ab, und das Schwankungsquadrat der regularisierten Feldoperatoren ist endlich, aber natürlich von der genauen Wahl von φ(r)
abhängig.
Regularisierungsmethoden sind fast unumgänglich, falls wir die Unschärferelation zwischen den Feldern E und B diskutieren wollen. Für die Operatoren Ei (r) und Aj (r0 ) erhält
man aus den Modenentwicklungen den Kommutator
X
c
[Ei (r), Aj (r0 )] =
eki (r) [Qk , Pk0 ]
ek0 j (r0 )
0
ω
k
kk0
X
= i~c
ωk−1 eki (r)ekj (r0 ).
k
Die Funktionen ek (r) bilden aber einen vollständigen Satz von Funktionen im Raum der
rein transversalen Vektorfelder:
X 1
⊥
eki (r)ekj (r0 ) = θij
(r − r0 ),
4πω
k
k
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
23
⊥
wobei θij
den Projektionsoperator auf die transversalen Felder darstellt. Dessen Fouriertransformierte ist bekanntlich
⊥
(k) ∼ δij −
θij
ki kj
;
k2
die r-Darstellung werden wir nicht brauchen, weil wir letztendlich am Kommutator zwischen Ei und Bj interessiert sind:
[Ei (r), Bj (r0 )] = 4πi~c jkl ∇0k θil⊥ (r − r0 ).
In dem Ausdruck für θil⊥ (k) ist der Zusatzterm rein longitudinal, und seine Rotation verschwindet. Der erste Term ist die Fouriertransformierte von δij δ(r − r0 ), so dass wir letztendlich erhalten
[Ei (r), Bj (r0 )] = 4πi~c ijk ∇0k δ(r − r0 ).
Dieser Ausdruck ist nur für verschmierte Felder sinnvoll:
Z
0
0
[Eφi (r), Bψj (r )] = 4πi~c ijk ∇k dr00 φ(r − r00 )ψ(r0 − r00 ).
Aus diesem Kommutator erhält man mit der üblichen Prozedur Unschärferelationen
zwischen Eφi (r) und Bψj (r0 ). Wie zuerst von Bohr und Rosenfeld analysiert wurde, sind
die Verhältnisse recht subtil: Um Eφ (r) scharf bestimmen zu können, muss ich die Funktion
φ ziemlich breit wählen. Dies impliziert aber, dass es auch ein relativ großes Gebiet gibt,
in dem ich Bψ (r0 ) nicht gleichzeitig scharf bestimmen kann. Die obige Analyse erweist sich
aber trotz ihrer Subtilität als für die Praxis nicht allzu bedeutsam; wie wir im nächsten
Abschnitt sehen werden, messen die meisten Detektoren nicht E oder B, sondern den
nichtdivergenten Anteil irgendeines quadratischen Ausdrucks in den Feldern. Gerade weil
die Vakuumfluktuationen so stark sind, empfiehlt es sich, Detektoren so zu konstruieren,
dass sie auf die Vakuumfluktuationen überhaupt nicht reagieren. Die obigen Überlegungen
dienen lediglich dazu, klar zu machen, dass die Messung der Felder Eφ und Bψ nicht zu
prinzipiellen Schwierigkeiten in der Theorie führt.
2.3
Das Strahlungsfeld in Wechselwirkung mit Atomen
In diesem Abschnitt betrachten wir ein Atom in Wechselwirkung mit dem Strahlungsfeld.
Der Einfachheit halber werden wir das Atom meistens durch ein Ein-Elektron-System ersetzen (Leuchtelektron-Näherung), und auch seine Schwerpunktsbewegung vernachlässigen.
Diese Einschränkungen lassen sich alle ohne viel Schwierigkeiten aufheben, allerdings auf
Kosten einer weiteren Komplizierung der Notation. Die Güte der Leuchtelektronnäherung
wird insbesondere auch im nächsten Kapitel noch zur Sprache kommen.
Wir werden annehmen, dass die Engergieeigenwerte und Eigenzustände des Atoms, ggf.
in hinreichender Näherung, bekannt sind, und sie mit dem Label A bezeichnen:
Hat |A = EA |A .
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
24
Der Hilbertraum des Gesamtsystems ist das direkte Produkt des Hilbertraumes für das
Atom und desjenigen für das Strahlungsfeld. Seine Basiszustände werden wir mit |A; {nk }
bezeichnen. Für die Physik spielen auch Superpositionen mit Korrelationen zwischen Atom
und Strahlungsfeld oft eine wesentliche Rolle.
Für die Einführung der Wechselwirkung zwischen Atom und Strahlungsfeld gibt es,
solange wir die Spinfreiheitsgrade außer Betracht lassen, eine universelle Vorschrift: Man
ersetze im atomaren Hamiltonoperator den Impulsoperator pi eines Teilchens mit der Ladung ei durch
pi −
ei
A(ri ),
c
wobei ri den Ortsoperator des betreffenden Teilchens darstellt. Weil man es in der Praxis
meist mit Elektronen zu tun hat, werden wir für ei auch e schreiben; diese Größe wird
dann negativ sein. Mit der obigen Substitution erhält man für die kinetische Energie des
Elektrons
2
1 e
e
e2
p2i
p
−
A(r
)
−
[p
A(r
)
+
A(r
)p
]
+
|A(ri )|2 .
=
i
i i
i
i
i
2m
c
2m 2mc
2mc2
In störungstheoretischen Rechnungen niedrigster Ordnung kann man den letzten Term
weglassen, weil seine Effekte in erster Ordnung mit den Effekten des ersten Terms in
zweiter Ordnung vergleichbar sind. Weiters kommutieren in Coulomb-Eichung die Operatoren pi und A(ri ); der Kommutator in Ortsdarstellung enthält nämlich ∇·A(r). Der
Wechselwirkungs-Hamiltonoperator beträgt also in niedrigster Ordnung
HI = −
e
pi A(ri ).
mc
Weil (e/m)pi als der vom Teilchen getragene Strom interpretiert werden kann, ist dieser
Ausdruck mit unserem Ausdruck für die Ankopplung an eine klassische Stromdichte analog.
Für ein Teilchen mit Spin hat man den Zusatzterm
HI0 = −
e~
~σi B(ri ),
2mc
auf dessen Herleitung wir in Zusammenhang mit der Dirac-Gleichung noch zurückkommen
werden.
2.3.1
Wahl der störungstheoretischen Behandlung
In der Quantenmechanik kennt man zwei theoretische Verfahren, die stationäre und die
zeitabhängige Störungstheorie. Für einen zeitunabhängigen Hamiltonoperator, wie er in
unserem Fall vorliegt, sind im Prinzip beide anwendbar. Für die Anwendung haben aber
beide ihre Vor- und Nachteile:
Die stationäre Störungsrechnung ist im Prinzip leistungsfähiger, aber sie wird recht
schwerfällig, wenn Entartung vorliegt. Dies ist für die von uns betrachteten Systeme immer
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
25
der Fall; der Zustand |A; {0} ist z.B. entartet mit allen |B; 1k mit EB < EA und ~ωk =
EA − EB . Die stationäre Störungsrechnung findet denn auch kaum Anwendung in der
Theorie des Strahlungsfeldes.
Die zeitabhängige Störungsrechnung beruht auf einer Störungsentwicklung für den
Evolutionsoperator im Wechselwirkungsbild. Sie ist insbesondere zugeschnitten auf die Behandlung von Prozessen, bei denen der Endzustand im kontinuierlichen Spektrum des
ungestörten Hamiltonoperators liegt. Allerdings ist dies eine Entwicklung nach der Zahl
der Male, die die Störung wirksam wird; der Formalismus ist also vor allem für kurz andauernde Prozesse geeignet, z. B. Zerfalls- oder Streuprozesse, bei denen das Photon
sich räumlich rasch vom Atom trennt. Für Atome in Hohlräumen oder Laserresonatoren trifft dies nicht zu; dort werden wir einen Teil des Wechselwirkungsoperators in den
ungestörten Hamiltonoperator herüberholen müssen. Auch für die Beschreibung der Wechselwirkung eines Atoms mit den Vakuumfluktationen des Strahlungsfeldes, die zur sog.
Lamb-Verschiebung Anlass gibt, muss die zeitabhängige Störungsrechnung etwas modifiziert werden.
2.3.2
Die Matrixelemente der Störung; Die Dipolnäherung
Der Hamiltonoperator
ie
e
HI = − p·A(r) = −
mc
m
r
~ X ek (r) p·
ak − a†k
2
ωk
k
bewirkt in erster Ordnung Störungstheorie Übergänge unter Emission oder Absorption eines einzelnen Photons. Die Matrixelemente von HI zwischen Basiszuständen sind aufgebaut
aus Atom- und Feldanteilen:
r
1
ie
~ X
A; {nk }|HI |B; {n0k } = −
A|p·ek (r)|B
{nk }| ak − a†k |{n0k } .
m 2 k
ωk
In erster Ordnung tragen nur Matrixelemente zwischen energetisch entarteten Zuständen
bei, d.h. solche in denen sich {nk } und {n0k } nur unterscheiden um eine einzelne Einheit
für eine einzelne Mode, für die weiters noch gilt ~ωk = |EB − EA |. Die Photonen
dieser
Mode haben relativ zur Ausdehnung des Atoms lange Wellenlängen. Falls A|p|B nicht
verschwindet, kann also ek (r) im Matrixelement durch ek (r0 ) ersetzt werden, wobei r0
die Lage des Atomschwerpunktes ist; ek (r0 ) kann außerhalb des Matrixelements gebracht
werden, weil es die Elektronenkoordinate nicht enthält. Für das verbleibende Matrixelement
gilt
im im(EA − EB ) A|p|B =
A| [Hat , r] |B = −
A|r|B .
~
~
(3.1)
Einsetzen dieses Ausdrucks in das obige Matrixelement liefert (unter Ausnützung von
~ωk = ±(EB − EA ), wobei das Vorzeichen für den ak - und den a†k -Beitrag unterschied-
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
26
lich zu wählen ist)
r
X
~
−e
A|r|B ·
ek (r0 ) {nk }|(ak + a†k )|{n0k } = −e A|r|B · {nk }|E(r0 )|{n0k } .
2
k
Ein Übergang mit A|r|B 6= 0 heißt elektrischer Dipolübergang; die Näherung, in der
ek (r) durch ek (r0 ) ersetzt wird, heißt Dipolnäherung. In dieser Näherung bewirken, wie
man leicht nachprüft, der A2 -Term und der B·~σ -Term überhaupt keine elektronischen
Übergänge mehr (sie enthalten weder r noch p). Die Äquivalenz
e
− A(r)·p ≈ −eE(r)·r,
mc
welche hier nur in Störungstheorie erster Ordnung bewiesen wurde [Ersetzen von ~ωk durch
±(EB − EA )] lässt sich innerhalb der Dipolnäherung zu einer Ersetzung der gesamten
Störung durch −eE(r)·r verallgemeinern (ohne Beweis!).
2.3.3
Kurze Rekapitulation der zeitabhängigen Störungstheorie
Wir betrachten ein System mit einem Hamiltonoperator
H = H0 + HI ,
wobei die Eigenwerte und Eigenvektoren von H0 bekannt sind:
H0 |i = Ei |i .
Wenn wir den Zustand des Systems darstellen durch
X
i
|ψ; t =
ci (t)e− ~ Ei t |i ,
i
so erhält man durch Substitution in die Schrödingergleichung den Satz gekoppelter Gleichungen
i
1 X
i|HI |j e ~ (Ei −Ej )t cj (t).
ċi (t) =
i~ j
Diese Gleichungen können iterativ gelöst werden. Für die Anfangsbedingung ci (0) = δia
erhält man in erster Ordnung
Z
i
1 t 0
0
(1)
dt f |HI |a e ~ (Ef −Ea )t .
cf (t) =
i~ 0
Gelegentlich werden wir auch die zweite Ordnung brauchen:
Z
i
1 X t 00 00 (1)
(2)
cf (t) =
dt f |HI |i e ~ (Ef −Ei )t ci (t00 )
i~ i 0
Z
Z 00
i
i
1 X t 00 t 0 00 0
=− 2
dt
dt f |HI |i e ~ (Ef −Ei )t i|HI |a e ~ (Ei −Ea )t .
~ i 0
0
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
Die Wahrscheinlichkeit, das System zur Zeit t im Zustand |f
Ordnung gegeben durch
Z
2 t 0 i (E −Ea )t0 2
1 (1)
2
.
|cf (t)| = 2 f |HI |a dt e ~ f
~
0
27
anzutreffen, ist in erster
Für großes t erhält man mit Hilfe der Formel
sin2 tx
= πδ(x)
t→∞ tx2
lim
den Ausdruck
(1)
|cf (t)|2 =
2
2π f |HI |a δ(Ef − Ea )t.
~
Ein solcher Ausdruck ist nur dann sinnvoll, wenn der Zustand |f in einem Kontinuum
(oder Gebiet sehr dichter Zustände) liegt. Falls weiters noch das Matrixelement in einem
Energiebereich um Ef nur schwach von Ef abhängt, so erhält man für die Übergangswahrscheinlichkeit pro Zeiteinheit wf nach der Fermi’schen goldenen Regel
wf =
2
2π f |HI |a ρf ,
~
wobei ρf die Zahl der Zustände vom Typ f pro Energieintervall um Ef bezeichnet. Wenn
es neben Ef noch einen kontinuierlichen Parameter des Endzustandes gibt, wie z.B. den
Raumwinkel dΩ, in den ein Photon emittiert oder gestreut wird, so definiert man entsprechende differentielle Übergangsraten wf,dΩ und Zustandsdichten ρf,dΩ .
2.3.4
Emission und Absorption von Strahlung
Wir betrachten jetzt als Anfangszustand den Zustand |A; {0} , wobei |A ein angeregter
atomarer Zustand ist, der Einfachheit
halber ein s-Zustand. Wegen der Auswahlregeln
für das Matrixelement B|r|A sind Dipolübergänge nur nach p-Zuständen möglich. Als
Modenfunktionen für die Photonen wählen wir die ebenen Wellen
r
4πωk ik·r
êi e ,
eki (r) =
V
wobei wir die êi so wählen, dass êi in der (k, êz )-Ebene
liegt und ê2 darauf senkrecht
steht. Beim Übergang vom Zustand |A nach |B, lz = 0 kann dann nur ein Photon der
Polarisation êi emittiert werden. Wir werden weiters das Atom immer im Ursprung des
Koordinatensystems platzieren. Das Matrixelement für diesen Übergang beträgt
r
2πωk ~ B, 0; 1k1 |HI |A; {0} = −e
B, 0|z|A sin θ,
(3.2)
V
wobei θ den Winkel zwischen k und êz darstellt.
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
28
Zur Berechnung der Zerfallsrate brauchen wir noch die Zahl der Modenfunktionen mit
Energie zwischen ~ω und ~ω + dE im Raumwinkel dΩ um die Richtung k. Die Dichte der
erlaubten k-Werte im k-Raum ist
3
V
L
dk =
dk.
ρk dk =
2π
8π 3
In einem Ausschnitt dΩ einer Kugelschale um ω = ck mit der Dicke dE = d(~ck) befinden
sich also
V ω2
ρE,dΩ dEdΩ = 3 3 dEdΩ
8π ~c
erlaubte k-Werte. Für die Zerfallsrate erhalten wir also mit Hilfe der goldenen Regel
wE,dΩ =
2
e2 ω 3
sin2 θ B, 0|z|A .
3
2π~c
Weil e2 /~c die dimensionslose Feinstrukturkonstante α ≈ 1/137 ist, hat dieser Ausdruck
die Dimension einer
inversen Zeit, wie für eine Rate zu erwarten war. Um die Lebensdauer
des Zustandes |A zu berechnen müssen wir
R
a) integrieren über alle Richtungen von k; dies liefert einen Faktor dΩ sin2 θ = 8π/3
b) summieren über die 3 Subniveaus von |B : ein Faktor 3
B
c) summieren über alle p-Niveaus |B mit EB < EA . Dabei soll ω durch ωAB = EA −E
~
ersetzt werden.
Das Ergebnis ist
wA =
0
2 3
1
4e2 X = 3
B|z|A ωAB
.
τA
~c B
(3.3)
Für Absorption und stimulierte Emission ist dasselbe atomare Matrixelement (3.2) verantwortlich (oder dessen komplex konjugiertes). Bei der Auswertung der goldenen Regel
muss jetzt aber beachtet werden, dass der Endzustand diskret ist,
während der Anfangszu √
stand im Kontinuum liegt. Das relevante Feld-Matrixelement ist {nl −δkl }|ak |{nl } = nk ;
Die Rate (3.3) geht also über in die Rate für die Absorption oder stimulierte Emission durch
Multiplikation mit der Zahl hnk i, der mittleren Zahl der Photonen pro Mode.
Betrachte jetzt einen Hohlraum, in dem sich ein Atom befindet. Im thermischen Gleichgewicht müssen die Raten für Absorption und (stimulierte + spontane) Emission einander
die Waage halten. Wenn wir die Wahrscheinlichkeiten, dass sich das Atom im Zustand |C
befindet, mit pC bezeichnen, so muss gelten:
hnk i pB = (hnk i + 1)pA .
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
29
Weil im thermischen Gleichgewicht
pA = e−β(EA −EB ) pB = e−β~ωk pB
gelten muss, erhalten wir also für hnk iβ , der mittleren Quantenzahl pro Mode, den für
Bosonen bekannten Wert
hnk iβ =
1
eβ~ω
−1
.
Mit diesem Argument wurde zuerst von Einstein die Planck’sche Formel für die Energiedichte der Hohlraumstrahlung
U (ω)dω =
~ω 3
1
dω
3
β~ω
πc e
−1
hergeleitet (vgl. Skriptum Thermodynamik).
2.3.5
Streuung von Photonen
Als nächstes betrachten wir die Streuung eines Photons an einem Atom. Das relevante
Matrixelement ist
B; 1k0 j |HI |A; 1ki .
In diesem Matrixelement kommt nur der A2 -Term zum Tragen, weil wenigstens ein Erzeuger
und ein Vernichter auftreten muss. In der Dipolnäherung erhält man
√
e2 4π ωk ωk0 c2 ~ †
†
0 j |a 0 aki + aki a 0 |1ki
B; 1k0 j |HI |A; 1ki = B|A êj êi
1
k
kj
kj
2mc2
V
2ωk ωk0
2πe2 ~
= δAB êj êi
√
mV ωk ωk0
Der A2 -Term führt also nur zu elastischer Streuung.
In derselben Ordnung der Störungstheorie müssen aber auch Terme mitgenommen werden, in denen der Term erster Ordnung zweimal wirkt:
t00
t0
|A; 1ki −
→ |C; {0} −
→ |B; 1k0 ,j
und
t00
t0
|A; 1ki −
→ |C; 1ki 1k0 j −
→ |B; 1k0 ,j
Der intermediäre Zustand wird i.a. nicht mit Anfangs- und Endzustand energetisch entartet
sein (dieser Ausnahmefall der resonanten Streuung bedarf einer separaten Diskussion).
30
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
Salopp gesagt darf das System diesen Zustand aber für eine kurze Zeit ∆t ∼ ~/∆E innehaben; solange ”bemerkt” das System die Verletzung der Energieerhaltung wegen der EnergieZeit-Unschärferelation nicht (eine genauere mathematische Begründung folgt gleich). Die
drei Beiträge zur Streuung werden oft wie folgt graphisch dargestellt:
B
k! , j
B
k! , j
C
k, i
A
A
B
k! , j
C
k, i
A
k, i
Graphen eines ähnlichen Typs wurden zuerst von Feynman zur Veranschaulichung
von Rechnungen in der (relativistischen) Quantenelektrodynamik eingeführt; sie werden
deshalb als Feynmangraphen bezeichnet. Feynman führte auch Regeln ein, die es erlauben,
an Hand des Graphen sofort das zugehörige Matrixelement zu bestimmen. Wir werden
statt dessen die Matrixelemente auf konventionelle Art bestimmen.
Der Beitrag des ersten Diagramms zur Übergangsamplitude beträgt, wie man durch
(1)
Substitution des Matrixelements in den allgemeinen Ausdruck für cf sieht,
Z t
i
2πe2
0
(1)
δAB êj ·êi
dt0 e ~ (EB +~ωk0 −EA −~ωk )t
cf,I (t) = −
√
imV ωk ωk0
0
i
2πe2 ~ e ~ (EB +~ωk0 −EA −~ωk )t − 1
δAB êj ·êi .
=
√
mV ωk ωk0 EB + ~ωk0 − EA − ~ωk
Die mit dem zweiten Diagramm assoziierte Amplitude beträgt
√
1 4π ωk ωk0 c2 ~
e2 X
(2)
cf,II = − 2
êj ·pBC pCA ·êi
~
V
2ωk ωk0 m2 c2 C
Z t
Z t00
i
00 i
0
00
dt
dt0 e ~ (EB +~ωk0 −EC )t e ~ (EC −EA −~ωk )t ,
×
0
0
wobei wir die Abkürzungen pBC = B|p|C usw. eingeführt haben. Das Doppelintegral ist
elementar auswertbar:
Z t
Z t00
Z
i
00
~ t 00 i (EB +~ωk0 −EC )t00 e ~ (EC −EA −~ωk )t − 1
00
0
~
dt e
dt
dt . . . =
i 0
EC − EA − ~ωk
0
0
" i
#
i
e ~ (EB +~ωk0 −EA −~ωk )t − 1 e ~ (EB +~ωk0 −EC )t − 1
~2
=−
−
.
EC − EA − ~ωk EB + ~ωk0 − EA − ~ωk
EB + ~ωk0 − EC
Bei der Auswertung der Übergangsrate liefert der zweite Term (im Limes t → ∞) einen
Beitrag proportional zu δ(EB + ~ωk0 − EC ); dieser trägt nur bei, falls der Endzustand mit
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
31
einem intermediären Zustand |C; {0} entartet ist. Dies ist der Fall resonanter Streuung,
den wir ausgeschlossen haben.
Es gibt einen zweiten, etwas subtileren Grund, weshalb der zweite Term physikalisch
nicht relevant ist. Ein Indiz dafür ist dieoffensichtliche
Nichterhaltung der Energie, sowie
der Umstand, dass der Übergang |A; 1ki → |C; {0} unmittelbar zur Zeit t = 0 stattzufinden scheint. Das Auftreten dieses Terms hat damit zu tun, dass der Ausgangszustand
|A;1ki nur in niedrigster Ordnung dem physikalisch gemeinten Zustand (Atom im Zustand
|A + ein Photon der Sorte ki) entspricht.
[Der physikalische Anfangszustand ist genau
betrachtet nicht der Eigenzustand |A; 1ki des ungestörten Operators, sondern der Zustand
der daraus nach ”sanftem” Einschalten
der Störung H1 entsteht. Letzterer enthält u.a. eine
Beimischung des Zustandes |C; {0} , deren Berücksichtigung zu einem Beitrag führt, welcher denjenigen des zweiten Terms in der obigen Formel genau aufhebt. Da diese Effekte
bei den nichtresonanten Beiträgen bis zur betrachteten Ordnung aber ohnehin keine Rolle
spielen, werden wir den dazu benötigten Formalismus nicht näher diskutieren.]
(2)
Mit einer ähnlichen Rechnung lässt sich auch der Beitrag cf,III des dritten Diagramms
berechnen. Das Doppelintegral liefert
" i
#
i
~2
e ~ (EB +~ωk0 −EA −~ωk )t − 1 e ~ (EB −EC −~ωk )t − 1
−
.
−
EC + ~ωk0 − EA EB + ~ωk0 − EA − ~ωk
EB − EC − ~ωk
Der zweite Term trägt nur dann bei, wenn |B; {0} mit |C; 1ki entartet ist, also wieder
nur für den bereits ausgeschlossenen Resonanzfall; wir werden ihn weiters weglassen. Wir
erhalten also für sämtliche Beiträge zu cf (t) denselben Zeitfaktor:
"
#
X êj ·pBC pCA ·êi
2πe2 ~
êj ·pCA pBC ·êi
cf (t) = − 2 √
mδAB êj ·êi −
+
m V ωk ωk 0
E
EC + ~ωk0 − EA
C − EA − ~ωk
C
i
e ~ (EB +~ωk0 −EA −~ωk )t − 1
×
.
EB + ~ωk0 − EA − ~ωk
Aus dem Betragsquadrat dieses Ausdrucks erhält man mittels einer Rechnung, die der
Herleitung der Zerfallsrate völlig analog ist, für die Übergangsrate in einen Endzustand
mit dem Photon k0 j in einem Raumwinkel dΩ
2
2π 4π 2 e4 ~2 V ωk20
. . . dΩ
wf dΩ =
~ m2 V 2 ωk ωk0 8π 3 ~c3
2
c ωk0
e4
= 2 4 2
. . . dΩ.
m c m V ωk
Üblicherweise gibt man statt der Übergangsrate den Streuquerschnitt an, definiert
als die Übergangsrate
dividiert durch die einfallende Photonenstromdichte. Weil sich
im Zustand |1ki ein Photon im Volumen V befindet, welches sich natürlich mit der Lichtgeschwindigkeit bewegt, ist die Stromdichte in unserem Fall c/V . Falls man weiters noch den
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
32
klassischen Elektronenradius r0 = e2 /mc2 einführt, erhält man für den differentiellen
Streuquerschnitt
2
X
0
ω
dσ
1
ê
·p
p
·ê
ê
·p
p
·ê
k j BC CA i
j CA BC i
= r02
+
δAB êj ·êi −
.
dΩ
ωk m C EC − EA − ~ωk EC + ~ωk0 − EA Diese Formel wurde zuerst von Kramers und Heisenberg mit Hilfe der alten Quantentheorie hergeleitet; die in dieser Formel auftretende Struktur hat Heisenberg zur Idee der
Matrixmechanik geführt.
Bei der Streuung eines Photons muss immer Energieerhaltung gelten: Falls A = B
gilt auch ωk = ωk0 ; man spricht dann von elastischer Streuung. Streuung mit Änderung
des atomaren Zustandes (oder allgemeiner, des Zustandes des Systems, an welchem gestreut
wird) heißt Raman-Streuung. Je nachdem ob das Photon seine Energie erniedrigt oder
erhöht, spricht man von Stokes oder Anti-Stokes-Linien im Streuspektrum.
Rayleigh-Streuung
Wir betrachten jetzt insbesondere die elastische Streuung eines Photons an einem Atom
im Grundzustand. Weiters soll die Energie des Photons klein sein gegenüber sämtlichen
atomaren Anregungsenergien EC − EA . Wir können dann die Resonanznenner entwickeln
gemäß:
1
~ω
1
=
+ ... .
+
EC − EA − ~ω
EC − EA (EC − EA )2
Falls wir weiters noch die in Gleichung (3.1) hergeleitete Beziehung
pAC =
im(EA − EC )
rAC
~
verwenden, so erhält man für den Streuquerschnitt
2
"
#
X
dσ
i
2
= r0 êj ·êi − êj ·
(pAC rCA − rAC pCA ) ·êi + . . . .
dΩ
~
C
Aus der Vollständigkeit der Zustände |C kann man schließen, dass der Ausdruck in eckigen
Klammern der Kommutatorausdruck
~~
A| [p, r] |A = I~
i
ist. Die oben angegebenen Terme heben sich also auf; das gleiche gilt für die Terme der
Ordnung (~ω)2 , und der Streuquerschnitt ist bestimmt von der dritten Ordnung in ~ω:
"
# 2
r 2
X
dσ
1
0
=
~4 ωk4 êj ·
(p
p
+
p
p
)
·ê
AC CA
AC CA
i .
3
dΩ
m
(EC − EA )
C
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
33
In niedrigster Ordnung in ω erhalten wir also die bekannte ω 4 -Abhängigkeit, die zuerst
von Lord Rayleigh für die Streuung an einem harmonisch gebundenen Elektron hergeleitet wurde. Der Effekt erklärt die blaue Farbe des Himmels, sowie die rote Farbe der
untergehenden Sonne. Weil der aus den pAC gebildete Tensor bei Summation über alle
C-Zustände
(und, falls |A kein s-Zustand ist, bei Mittelung über die lz -Unterzustände
von |A ) zur Einheitsmatrix proportional ist, ist auch der Polarisationszustand des Streulichtes und seine Winkelverteilung leicht anzugeben (siehe Skriptum Elektrodynamik für
eine Ausarbeitung).
2.4
Das Atom im Strahlungsfeld: Spezielle Probleme
2.4.1
Idealisierte Photodetektoren
In diesem Abschnitt betrachten wir als idealisiertes Modell eines Photodetektors ein Atom,
in dem die im Feld vorhandenen Photonen immer Übergänge ins Kontinuum, also Photoionisation erwirken. Weiters erweist es sich als zweckhaft, die Wechselwirkung HI in
Dipolnäherung und im Wechselwirkungsbild zu betrachten:
HI (t) = −eE(r0 , t)·r(t).
Das Matrixelement zwischen einem Anfangszustand |A; a und einem Endzustand |F ; f
beträgt dann
F ; f |HI (t)|A; a = −e F |r(t)|A · f |E(r0 , t)|a
= −e eiωF A t rF A · f |E(r0 , t)|a .
In niedrigster Ordnung trägt nur der Vernichter-Anteil von E, weiters mit E(+) (r0 , t) bezeichnet, bei. Für die Wahrscheinlichkeit p1 (t), dass im Intervall (0, t) überhaupt ein Übergang dieser Art stattfindet, erhält man
X X ie Z t
2
0 iωF A t0
(+)
0
dt e
rF A · f |E (r0 , t )|a p1 (t) =
~
0
F
f
(4.1)
Z
e 2 X t Z t
00
0
=
dt00 eiωF A (t −t ) r∗F A ·G1a (r0 , t0 ; r0 , t00 )·rF A ,
dt0
~
0
0
F
wobei wir die Abkürzung
G1a (r0 , t0 ; r1 , t00 ) = a|E(−) (r0 , t0 )E(+) (r1 , t00 )|a
eingeführt haben; E(−) bezeichnet den Anteil von E. Bei der Herleitung
von (4.1) wurden
der Ausdruck für cf (t) und die Vollständigkeit der Zustände |f benutzt. Man überprüft
leicht, dass für G1a die alternative Darstellung
G1a (r1 , t1 ; r2 , t2 ) =
1
a| : E(r1 , t1 )E(r2 , t2 ) : |a
2
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
34
gilt. Dies bestätigt die auf S. 20 gemachte Aussage, dass in ”vernünftigen” Messanordnungen
nur normal geordnete Produkte von Feldoperatoren gemessen werden.
Der Ausdruck (4.1) lässt sich noch etwas umschreiben durch Einführung des Empfindlichkeitstensors
e 2 X
r∗F A rF A δ(ω − ωF A );
(4.2)
S(ω) = 2π
~
F
Substitution in (4.1) ergibt
Z t Z t
Z +∞
1
00
0
0
00
p1 (t) =
dt
dt
dω eiω(t −t ) S(ω) : G1a (r0 , t0 ; r0 , t00 )
2π 0
0
−∞
Eine weitere Vereinfachung erfolgt über die Fourier-Transformierte
Z +∞
1
S(t) ≡
dω eiωt S(ω);
2π −∞
Einsetzen dieser Größe liefert
Z t Z t
p1 (t) =
dt0
dt00 S(t00 − t0 ) : G1a (r0 , t0 ; r0 , t00 ).
0
0
Zwischenbemerkung
Der S-Tensor-Formalismus erlaubt auch die Berücksichtigung weiterer experimentell relevanter Faktoren: man kann hinter der Summation
in (4.2) einen Faktor RF einführen, der
die Nachweiswahrscheinlichkeit des in |F enthaltenen Photoelektrons repräsentiert.
Dadurch wird p1 (t) zur Wahrscheinlichkeit, dass ein Photon (über den Prozess der Photoionisation) detektiert wird. Auch der Effekt von vor dem Detektor platzierten Frequenzoder Polarisationsfiltern lässt sich durch eine Abänderung von S(ω) berücksichtigen.
In der Praxis wird man für Detektion von Licht bevorzugt solche Atome wählen, die im
für das Experiment relevanten Frequenzbereich eine möglichst konstante Empfindlichkeit
haben und die weiters nicht polarisationsselektiv sind:
S(ω) ' s0 I;
S(t) ' s0 I δ(t).
In dieser Näherung gilt
Z t
p1 (t) = s0
dt0 I : G1a (r0 , t0 ; r0 , t0 ).
0
Die Detektionsrate w1 (t) =
|E(r0 , t)|2 : proportional!
d
p (t)
dt 1
ist dann tatsächlich zum Erwartungswert von :
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
2.4.2
35
Die Koinzidenz zweier Detektoren
Als Nächstes betrachten wir die Situation, dass sich im Feld zwei Ein-Atom-Detektoren
(mit gleichen Atomen) an den Orten r10 und r20 befinden. Wir suchen die Wahrscheinlichkeit dafür, dass im Zeitintervall (0, t) beide Detektoren
ein Photon detektieren. Die
Basiszustände des Hilbertraumes haben die Form |B1 ; C2 ; i , wobei B1 z.B. andeutet, dass
Atom 1 sich im Zustand B befindet, und wir suchen nach Übergängen vom Typ
|A1 ; A2 ; a → |F1 ; G2 ; f .
Solche Übergänge erfordern zwei ”Eingriffe” von HI (der A2 -Term bewirkt keine Übergänge
und kann vernachlässigt werden) und zwar jeweils einen von den beiden Termen in die HI
zerlegt werden kann:
HI (t) = HI1 (t) + HI2 (t),
wobei HIi (t) nur die Wechselwirkung zwischen Feld und Atom i enthält. Die Übergansamplitude für den obigen Übergang beträgt also
Z 0
Z
−1 t 0 t 00
dt [HI1 (t0 )HI2 (t00 ) + HI2 (t0 )HI1 (t00 )] |A1 ; A2 ; a . (4.3)
dt
cF Gf (t) = F1 ; G2 ; f | 2
~ 0
0
(+)
(−)
Jedes der HI,i (t) kann wieder geschrieben werden als HIi (t)+HIi (t), wobei die ±-Anteile
die Vernichter bzw. Erzeuger von Photonen enthalten. Weil für den gesamten Übergang
Energieerhaltung gelten muss, und der atomare Anteil der Energie auf jeden Fall zunimmt,
(+)
muss im obigen Ausdruck jeder Term mindestens ein HIi enthalten. Beiträge, bei denen im
anderen Faktor der Anteil H (−) eine Rolle spielt, treten auf, aber sie sind, relativ zu Termen,
in denen von beiden HIi der (+)-Anteil auftritt, von der Ordnung (ωF A t)−1 (Der Beweis
(+)
wird dem Leser als Übungsaufgabe überlassen). Weil die HIi miteinander kommutieren
(sie enthalten als Feldoperatoren nur Vernichter; die auftretenden atomaren Operatoren
wirken auf verschiedene atomare Freiheitsgrade), kann der so erhaltene dominante Anteil
von cF Gf (t) auch geschrieben werden als
Z
Z
−1 t 0 t 00 (+) 0 (+) 00
dt
dt HI1 (t )HI2 (t )|A1 ; A2 ; a
F1 ; G2 ; f | 2
~ 0
0
[zum Beweis: abgesehen von der Reihenfolge der Operatoren ist die Differenz zwischen
den Termen in (4.3), dass im ersten Term HI2 und im zweiten Term HI1 zuerst wirkt.
Eine Umbenennung der Integrationsvariablen führt sofort zum obigen Ausdruck]. Eine
Ausarbeitung des Matrixelements liefert
e 2 Z t Z t
0
00
dt0
dt00 eiωF A t eiωGA t (rF A rGA ) : f |E(+) (r20 , t00 )E(+) (r10 , t0 )|a .
~
0
0
Die mit Hilfe dieses Ausdrucks berechnete Wahrscheinlichkeit p2 (t) für das Auftreten von
Ionisation in beiden Detektoren
XXX
|cF Gf (t)|2
p2 (t) =
F
G
f
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
36
kann jetzt genauso wie p1 (t) umgeformt werden durch Einführung
der Empfindlichkeitstensoren und Ausnützung der Vollständigkeit der Feldzustände |f . Das Ergebnis ist
Z t
Z t
XZ t Z t
0
00
000
p2 (t) =
dt
dt
dt
dt0000 Sil (t0000 − t0 )Sjk (t000 − t00 )
0
ijkl
0
0
0
0000
000
00
0
× G2,a
ijkl (r10 , t ; r20 , t ; r20 , t ; r10 , t ),
mit der Definition
(−)
(−)
(+)
(+)
G2,a
ijkl (xi ; xj ; xk ; xl ) ≡ a|Ei (xi )Ej (xj )Ek (xk )El (xl )|a ,
wobei xi für das Paar (ri0 , ti ) steht. Man überprüft leicht, dass auch G2,a als Erwartungswert
eines normal geordneten Operators aufgefasst werden kann. Für breitbandige, isotrope
Detektoren vereinfacht sich der Ausdruck für p2 (t):
XZ t Z t
0
00
00
0
2
dt0
dt00 G2,a
p2 (t) = s0
ijji (r10 , t ; r20 , t ; r20 , t ; r10 , t ).
ij
0
0
Für diesen Fall lässt sich also eine Koinzidenzrate
X 2,a
w2 (t1 , t2 ) = s20
Gijji (x1 ; x2 ; x2 ; x1 )
ij
definieren. Im allgemeinen sind die zwei Prozesse, trotz der dynamischen Unabhängigkeit
der beiden Detektoren, korreliert:
w2 (t1 , t2 ) 6= w1 (t1 )w2 (t2 ).
Der Bosecharakter der Photonen
Die Größe G2,a
ijji (x1 ; x2 ; x2 ; x1 ) lässt sich für Breitbanddetektoren also definieren als die Rate,
womit sowohl ein Photon mit Polarisation i zur Zeit t1 in der Nähe von r10 als auch ein
Photon mit Polarisation j zur Zeit t2 in der Nähe von r20 detektiert wird. Es ist instruktiv,
diese Größe für den Zwei-Photonen-Zustand
|k, l ≡ |1k 1l = a†k a†l |{0}
zu berechnen. Das Ergebnis ist (beachte, dass in der Mitte des Ausdruckes für G2,kl der
Projektor |{0} {0}| hineingeschoben werden darf)
G2,a
ijji =
~2
|eki (r10 , t1 )elj (r20 , t2 ) + eli (r10 , t1 )ekj (r20 , t2 )|2 ,
2
also dem entsprechenden Betragsquadrat einer symmetrisierten Zwei-Teilchen-Wellenfunktion,
wie sie für Bosonen üblich ist, recht analog. Wir sehen insbesondere, dass neben den räumlichen und den Polarisationsindizes auch die Zeitpunkte in den beiden Termen miteinander
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
37
vertauscht werden müssen; in dieser Hinsicht geht der hier behandelte Formalismus über
den aus der Vorlesung Quantenmechanik bekannten hinaus. Ein weiterer Unterschied zu
dem bekannten Formalismus ist noch, dass hier nicht die Ein-Teilchen-Wellenfunktionen
fk (r), eingeführt auf S. 15, auftreten, sondern die Feldamplitudenfunktionen ek (r); dies
hat damit zu tun, dass der hier beschriebene Photodetektor mit konstantem S(ω) auf die
Größe : |E(r, t)|2 : anspricht. Für die Wahl S(ω) ∼ ω −1 wären in der obigen Formel die fk
vorgekommen; dies wäre aber eine recht spezielle, praktisch nicht leicht realisierbare Wahl
(sogar falls die Bedingung nur über einen beschränkten Frequenzbereich zu gelten braucht).
Kohärente Zustände des Feldes sind Eigenzustände der E(+) (r, t). Für solche Zustände faktorisieren also die Feldkorrelationsfunktionen G 1 und G 2 , und es treten keinerlei Korrelationen zwischen unterschiedlichen Detektoren auf. Mit einer maximalen Bestimmtheit
dieser Zustände vom Wellenaspekt her korrespondiert also eine maximale Stochastizität
des Teilchenaspektes des Feldes.
Mehrfachkoinzidenzen von mehr als zwei Detektoren können auf völlig ähnliche Weise diskutiert werden. Eine ausführlichere Behandlung von Photodetektion und der Statistik
von Photoelektronen findet man in den Vorlesungen von Glauber in der Sommerschule von
1964 in Les Houches (Quantum Optics and Electronics, C. DeWitt et al., Hrsg., Gordon
and Breach, New York, 1965).
2.4.3
Ein Atom in einem Resonator
In diesem Abschnitt betrachten wir ein Atom in einem Laser- oder Hohlraumresonator,
der eine Eigenfrequenz besitzt, welche mit einem erlaubten Übergang des Atoms fast resonant ist. Ein im angeregten Zustand in den Resonator hineingebrachtes Atom wird rasch
zerfallen, aber das emittierte Photon wird dann von den Spiegeln oder Wänden auf das
Atom zurückreflektiert und mit einer gewissen Wahrscheinlichkeit wieder reabsorbiert. Zur
Beschreibung dieser Situation nehmen wir die Terme, die am effektivsten zu den atomaren Übergängen beitragen, im ungestörten Hamiltonoperator auf, und berechnen dann die
Eigenzustände des
so geänderten
H0 . Es zeigt sich, dass diese Zusatzterme
immer nur die
Zustände |A; n0 und |B; n0 − 1 miteinander mischt, wobei | A und | B die beteiligten
atomaren Zustände sind, und m0 der Zustand mit genau m Photonen in der fast resonanten
Feldmode, dessen Erzeuger und Modenfunktion wir mit a†0 bzw. e0 (r) bezeichnen werden.
Es reicht deshalb aus, den reduzierten Hamiltonoperator
1
†
0
H0 =EA |A A| + EB |B B| + ~ω0 a0 a0 +
2
r
(4.4)
h
i
~
−e
e0 (r0 )·rAB a†0 |A B| + a0 |B A|
2
zu betrachten, wobei wir uns einfachheitshalber auf den Fall reeller e0 (r) und
rAB be-
schränkt haben. Die Matrixelemente von H00 bezüglich der Basisvektoren |e1 = |A; n0
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
38
und |e2 = |B; n0 − 1 bilden die 2x2 Matrix
√ 1
~ω√
−~g n
0
EA + n −
.
~ω0 I +
~ωat
−~g n
2
Dabei haben wir die Abkürzungen
~ωat = EB − EA ;
e
g = − √ e0 (r0 )·rAB
2~
eingeführt und die Bezeichnung I für die Einheitsmatrix verwendet. Die obige Matrix hat
die Eigenwerte
1
1
1 p
~ωn± = EA + n −
~ω0 + ~(ω0 + ωat ) ± ~ (ωat − ω0 )2 + 4ng 2
2
2
2
1
1 p
= (EA + EB ) + n~ω0 ± ~ (∆ω)2 + 4ng 2 .
2
2
Die zugehörigen Eigenzustände sind
|n + = cos θn |A; n − sin θn |B; n − 1 ;
|n − = sin θn |A; n − cos θn |B; n − 1 ,
wobei
#
"p
√ (∆ω)2 + 4ng 2 − ∆ω
1
2g n
√
= arctan
θn = arctan
.
2
∆ω
2g n
Für genaue Resonanz (∆ω = 0) gilt immer θn = 45◦ . Die hier diskutierte Hamiltonfunktion
kann auch für ein Atom in einem sehr intensiven Laserstrahl benutzt werden. Der Sonderstatus einer einzelnen Mode des Feldes folgt dann aus der sehr hohen Besetzungszahl, nicht
aus der Diskretheit des Spektrums.
Betrachte jetzt den Fall, dass sich das System zur Zeit t = 0 im Zustand |B, n − 1
befindet. Wegen
|B, n − 1 = − sin θn |n + + cos θn |n −
gilt für den Zustand |t zur Zeit t bis auf einen Phasenfaktor
|t = − sin θn e−iωRn t |n + + cos θn eiωRn t |n −
= i sin 2θn sin ωRn t|A; n + [cos ωRn t + i cos 2θn sin ωRn t]|B; n − 1 .
Der Zustand oszilliert also mit der Rabi-Frequenz
ωRn =
1/2
1
(∆ω)2 + 4ng 2
2
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
39
zwischen den zwei Komponenten |A; n und |B; n − 1 , und zwar für exakte Resonanz
(∆ω = 0) vollständig, für endliche Verstimmung nur mit der Amplitude sin2 2θn . Die RabiOszillatoren können dadurch experimentell beobachtet werden, dass man einen Strahl von
Atomen quer durch einen starken Laserstrahl schießt und die Fluoreszenz beobachtet, d.h.
spontane Zerfälle unter Emission eines Photons, deren k-Vektor nicht parallel zum Laserstrahl zeigt. Die Intensität des Fluoreszenzlichtes ist dann entlang des Strahls räumlich
moduliert mit einer Wellenlänge
λ = 2π
vat
,
ωRn
wobei vat die Geschwindigkeit der Atome im Strahl darstellt.
Laser
Atome
Im Spektrum der Fluoreszenzstrahlung sind die vier Kombinationsfrequenzen
ω0 ± ωRn ± ωR,n−1
im Prinzip alle vertreten. Dabei ist die Differenz zwischen ωRn und ωR,n−1 experimentell
nie auflösbar, wenn ωRn selbst hinreichend groß ist. Man erhält also drei Komponenten mit
den Intensitätsverhältnissen
sin4 θn : 2 sin2 θn cos2 θn : cos4 θn .
√
Für |∆ω|√ g n gilt θn ' 45◦ und das Intensitätsverhältnis ist näherungsweise 1:2:1. Für
∆ω g n gilt
1
1
ωn− ' EB + n −
~ω0 ;
ωn−1,+ = EA + n −
~ω0 ;
2
2
√
g n
θn '
1,
∆ω
also die Intensität liegt fast vollständig bei der Frequenz ωn− −√
ωn−1,+ ' ωat , der unverschobenen atomaren Frequenz. Für allgemeine Werte von 2g n/∆ω findet man ein
Intensitätsverhältnis zwischen den beiden Extremen; für den gewichteten Mittelwert der
Emissionsfrequenz erhält man mit Hilfe einiger trigonometrischer Beziehungen immer die
unverschobene atomare Frequenz ωat .
40
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
Bemerkung
Für die obige Betrachtung ist wesentlich, dass jeweils nur ein Atom mit dem Feld wechselwirkt. Falls mehrere Atome vorhanden sind, so wird i.a. die Modenfunktion an den
verschiedenen Orten einen etwas anderen Wert haben, und auch die Verstimmung wird auf
Grund der Dopplerverschiebung leicht unterschiedliche Werte haben; die Rabi-Oszillationen
verschiedener Atome geraten also rasch außer Takt.
2.4.4
Energieverschiebungen durch Ankopplung an die Vakuumfluktuationen (die Lamb-Verschiebung)
In diesem letzten Abschnitt des Kapitels über die Quantentheorie des Strahlungsfeldes
betrachten wir den Einfluss der Ankopplung an das Strahlungsfeld auf die Lage der atomaren Niveaus. Eine quantitativ zuverlässige Behandlung dieser Effekte kann nur im Rahmen
einer voll-relativistischen Theorie gegeben werden. Die nachfolgende nicht-relativistische
Beschreibung liefert aber schon eine Erläuterung der grundlegenden physikalischen Ideen,
sowie eine überraschend gute vorläufige Abschätzung der Größenordnung des zu erwartenden Effekts.
Konkret betrachten wir das System (Atom + Feld) im Zustand |A; {0} . Die Wech-
selwirkung HI bewirkt, dass dieser Zustand für eine kurze Zeit in einen Zustand |B; 1k
übergehen kann, und sich dann, ”ehe die entsprechende Verletzung der Energieerhaltung auf
Grund der Energie-Zeit-Unschärfe bemerkt werden kann”, wieder in den Zustand |A; {0}
zurückverwandelt. Auch kompliziertere Szenarien sind möglich; einige davon sind in der
untenstehenden Reihe von Graphen dargestellt.
A
A
A
A
A
D
D
C
C
C
B
B
D
B
k
A
(I)
k
A
(II)
A
(III)
k!
k
k!
k
A
(IV)
B
k!
k
A
(V)
Diese Umwandlungen haben zur Folge, dass die mittlere
Energie eines Systems, das
sich zu den Zeiten t = 0 und t = t1 im Zustand |A; {0} befindet, sich von der ungestörten
Energie EA etwas unterscheidet. Wir werden diesen Effekt in niedrigster Ordnung in e2
berechnen, d.h. wir betrachten nur die Graphen I und II, und zwar zuerst nur den Graphen
I; wir werden später ein Argument geben, weshalb der Graph II nicht zu beobachtbaren
Effekten führt.
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
41
Zum skizzierten Vorgehen betrachten wir also einen Zustand der allgemeinen Form
X
|t = cA (t)|A; {0} +
cBk (t)|B; 1k .
B,k
Wir vernachlässigen also Beimischungen von weiteren Zuständen. Weiters wissen wir aus
den Betrachtungen über den atomaren Zerfall (S. 27), dass für vorgegebene A, B und k
immer nur ein Polarisationszustand des Photons k ankoppelt. Für die Entwicklungskoeffizienten erhält man die Bewegungsgleichungen (hergeleitet auf S. 26)
i
(−)
i~ċBk (t) = B; 1k |HI |A; {0} e ~ (EB +~ωk −EA )t cA (t)
X
i
(+)
(4.5)
i~ċ (t) =
A; {0}|H |B; 1 e ~ (EA −EB −~ωk )t c (t),
A
I
k
Bk
B,k
wobei in Dipolnäherung gilt (vgl. S. 25 und 27)
∗
ie
(−)
(+)
B; 1k |HI |A; {0} = A; {0}|HI |B; 1k = −
m
r
2π~ ∗
0
ê ·pBA ≡ HBkA
.
V ωk k1
Die Elimination
von
pBA zugunsten von rBA ist hier nicht möglich, weil die Zustände
|A; {0} und |B; 1k nicht energetisch entartet zu sein brauchen!
Wir suchen jetzt eine Lösung des Systems (4.5) mittels des Ansatzes
i
cA (t) = e− ~ ∆EA t .
Dies ergibt
H0
cBk (t) = BkA
i~
0
= HBkA
Z
t
i
0
dt0 e ~ (EB +~ωk −EA −∆EA )t
0
i
(EB +~ωk −EA −∆EA )t
~
−1
e
.
(EA + ∆EA − EB − ~ωk
i
Substitution in die Gleichung (4.5) für cA , und Division durch e− ~ ∆EA t , liefert
i
∆EA =
X
B,k
2
0
|HBkA
|
1 − e ~ (EA −EB −~ωk )t
.
(EA − EB − ~ωk )
Im obigen Ausdruck haben wir auf der rechten Seite ∆EA gegenüber EA vernachlässigt,
weil wir ohnehin ∆EA nur bis zur Ordung e2 berechnen wollen (Mitnehmen von ∆EA , aber
nicht von ∆EB , wäre überdies auch inkonsistent). Die Zeitabhängigkeit im obigen Ausdruck
ist natürlich unphysikalisch; die Zeitfunktion soll durch ihren Grenzwert für t → ∞ ersetzt
werden. Um für das zugrundeliegende Integral einen wohldefinierten Wert zu erhalten, fügt
man im Exponenten einen kleinen Imaginärteil hinzu:
Z ∞
1 − eixt
0
lim
≡ − lim i
dt0 ei(x+iη)t
t→∞
η&0
x
0
1
x
iη
1
= lim
= lim 2
− 2
= − iπδ(x).
2
η&0 x + iη
η&0 x + η 2
x +η
x
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
42
Wir erhalten für ∆EA also einen komplexen Wert:
0
|HBkA
|2
EA − EB − ~ωk
B,k
X
2
0
Im(∆EA ) = −π
|HBkA
| δ(EA − EB − ~ωk ).
Re(∆EA ) =
X
B,k
Der Imaginärteil liefert (wegen ωk > 0) nur für angeregte Zustände einen Beitrag; in
dem Ausdruck
2π X 0
2
2
|H
| δ(EA − EB − ~ωk ) = wA
− Im(∆EA ) =
~
~ B,k BkA
erkennt man die mit Hilfe
der Fermi’schen goldenen Regel berechnete totale Zerfallsrate des Zustandes |A , die auf S. 28 explizit berechnet wurde, wieder. Diese Interpretation
wird unterstützt durch das Ergebnis
|cA (t)|2 = e+2Im(∆EA )t/~ |cA (0)|2 = e−wA t |cA (0)|2 .
0
Im Ausdruck für Re(∆EA ) substituieren wir jetzt den Wert des Matrixelements HBkA
.
3
Weiters ersetzen wir die Summe über k durch ein Integral, was den Faktor V /(2π) (gleich
der Dichte der zulässigen Werte im k-Raum) mit sich bringt:
Z
|ê∗k1 ·pBA |2
2π~e2 V X
1
dk
.
Re(∆EA ) = 2
m V 8π 3 B
ωk EA − EB − ~ωk
Als nächstes führen wir die Integration über die Winkel im k-Raum durch; dabei können
wir wie auf S. 28 die Beziehung
Z
Z
2
2
2
∗
dΩ |êk1 ·pBA | = |pBA |
dΩ sin2 θ = |pBA |2 4π
3
einsetzen. Falls wir weiters noch von der Integrationsvariablen |k| auf Eγ = ~ωk = ~ck
übergehen, erhalten wir
Z
2 e2 1 X ∞
Eγ |pBA |2
Re(∆EA ) =
dEγ
.
3π ~c (mc)2 B 0
EA − EB − Eγ
Dieser Ausdruck beruht auf einer nicht relativistischen Beschreibung des Elektrons und auf
der Dipolnäherung, die nur gilt, falls die Wellenlänge des Photons klein ist gegenüber den
sonstigen relevanten Längen im Matrixelement pBA . Beide Näherungen werden schlecht
für
hohe Werte von Eγ (Beachte, dass bei vorgegebenem Eγ sämtliche Zustände |B , für die
gilt EB − EA ∼ Eγ , noch beachtliche Beiträge liefern können; für hohe Werte von Eγ sind
dies ionisierte Zustände mit relativistischen Geschwindigkeiten des Elektrons). Sowohl die
Korrekturen zur Dipolnäherung als auch die relativistischen Korrekturen führen zu einer
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
43
starken Unterdrückung der Beiträge hoher Eγ . (Für die Korrekturen zur Dipolnäherung
ist dies evident: die Substitution
Z
Z
∂
∂
∗
ψB (r) ψA (r)dr −→ ψB∗ (r)e−ik·r ψA (r)dr
∂r
∂r
führt zum Verschwinden des Matrixelements im Limes |k| → ∞!)
Wir bringen diese Korrekturen jetzt ganz grob in Rechnung durch ein Abschneiden des
(max)
obigen Integrals bei einem, vorerst noch recht willkürlichen, Wert Eγ
. Zur Abschät(max)
zung von Eγ
kann folgende Überlegung dienen: Die Reduktion des Matrixelements
−ik·r
durch e
wird effektiv, sobald der Wellenvektor des Photons vergleichbar wird mit dem
Wellenvektor ke des Photoelektrons, der ohnehin in ψB∗ (r) vorkommt. Dies bedeutet konkret
r
2mEγ
Eγ
ke ∼
=⇒ Eγ ∼ 2mc2 .
∼
2
~
~c
(Der Faktor 2 ist natürlich nicht ernst zu nehmen, weil für E ∼ mc2 die nichtrelativistische
Beziehung zwischen E und ke längst nicht mehr gilt!) Auch nach diesem Abschneiden
ist der Ausdruck für Re(∆EA ) noch nicht wohldefiniert; er hängt noch sehr sensitiv von
(max)
Eγ
ab. Um zu einer vernünftigen Interpretation zu kommen, brauchen wir eine neue
physikalische Idee, die Massenrenormierung.
2.4.5
Intermezzo: Die Selbstenergie freier Elektronen
Die obige Rechnung für ein in einem Atom gebundenes
Elektron kann auch für ein freies
Elektron
durchgeführt
werden. Die Zustände |A und |B müssen dann durch die Zustände
|p und |p0 mit den Wellenfunktionen
1 i
r|p = √ e ~ p·r
V
ersetzt werden, und für das Matrixelement erhält man
r
Z
i
e
2π~
0
0
dr e ~ (p−p )·r e−ik·r (p·êk1 )
Hp0 kp = −
3
m ωk V
r
e
2π~
=−
p·êk1 δp0 ,p−~k .
m ωk V
Im Ausdruck für die Größe Re(∆Ep ), die auch als die Selbstenergie des Elektrons bezeichnet wird, tritt weiters noch der Energienenner
Ep − Ep0 − ~ωk =
p2
|p − ~k|2
−
− ~ωk ≈ −~ωk
2m
2m
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
44
auf, wobei die Abschätzung für nichtrelativistische Werte von k gültig ist:
p2
|p − ~k|2
p·~k ~2 k2
v
~ωk
−
=
+
=
·k̂ +
~ωk .
2m
2m
m
2m
c
2mc2
Einsetzen des Ausdrucks für Hp0 0 kp und der Näherung für den Energienenner im Ausdruck
für ∆Ep0 Ausführen der Winkelintegration, sowie ein Übergang zur Integrationsvariablen
Eγ , liefert einen rein reellen
Ausdruck
(gleichzeitige Erhaltung von Energie und Impuls
beim Übergang |p; {0} → |p0 ; 1k ist nicht möglich), und zwar
e2 2p2
∆Ep = −
~c 3π(mc)2
Z
0
(max)
Eγ
(max)
e2 2 Eγ
dEγ = −
p2 .
~c 3π (mc)2
Dieser Beitrag zur Energie eines freien Elektrons kann genauso behandelt werden wie
der Beitrag der potentiellen Energie zur Energie des Elektrons in einem periodischen Potential. Dafür erhält man z.B. im Kronig-Penney-Modell, und für genügend kleine p, einen
Ausdruck vom Typ
hV ip = c0 + c1 p2 .
In der Festkörperphysik ist es üblich, diesen Term über eine effektive Masse m∗ in Rechnung zu bringen:
p2
p2
+ hV i = c0 +
2m
2m∗
mit m∗ =
m
.
1 + 2mc1
Auf ähnliche Weise können wir jetzt schreiben
#
"
(max)
2
p2
e
4
E
γ
m,
Ep − ∆Ep =
mit
m∗ ∼
= 1+
2m∗
~c 3π mc2
(max)
was für die Wahl Eγ
= mc2 eine Korrektur von 0,3% bedeutet. Die Masse m∗ heißt in
diesem Zusammenhang auch renormierte Masse.
Die für die weitere Rechnung entscheidende, von Kramers stammende Idee ist jetzt:
Eine experimentelle Messung der Elektronenmasse bestimmt immer in m∗ und nicht die
im Hamiltonoperator aufscheinende ”nackte” Masse m. Auch die oben berechnete Niveauverschiebung ∆EA ist prinzipiell nicht beobachtbar; beobachtbar
ist nur der Unterschied
zwischen der Niveauverschiebung des im Zustand |A gebundenen Elektrons und der soeben bestimmten Absenkung der kinetischen Energie:
(obs)
∆EA
p2
p2 −
|A .
≡ ∆EA − A|
2m∗ 2m
Ehe wir diesen Ausdruck für die Niveaus des Wasserstoffatoms auswerten, diskutieren
wir noch kurz den Einfluss des Graphen II auf S. 40. Dieser führt zu einem Zusatzterm in
der Gleichung für ċA :
i~ċA = . . . +
e2 ~2 2
A;
{0}|A
(r)|A;
{0}
.
2mc2
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
45
In der Dipolnäherung kann A2 (r) durch A2 (r0 ) ersetzt werden. Letzterer Operator wirkt
nicht mehr auf die Elektronenkoordinaten, und man erhält
e2 ~2 2
A|A
{0}|A
(r
)|{0}
,
0
2mc2
also einen Beitrag zur Selbstenergie, der zwar ohne Abschneidung der k-Integration divergent ist, aber für alle Zustände gleich, und der deshalb prinzipiell nicht beobachtbar
ist. Man überzeugt sich leicht, dass auch für freie Elektronen (ohne Dipolnäherung!) ein
p-unabhängiger Beitrag, analog zur Größe c0 in der Festkörperanalogie, entsteht.
i~ċA = . . . +
Bethe’s Berechnung der Lamb-Verschiebung
Einsetzen der schon berechneten Werte für Re(∆EA ) und m∗ in den obigen Ausdruck
(obs)
(obs)
für ∆EA
liefert (wir werden weiters unter ∆EA
ohne nähere Angabe den Realteil
verstehen)
#
"
Z Eγ(max)
2
2
X
2
e
E
|p
|
γ BA
(obs)
+ (p2 )AA
dEγ
∆EA =
~c 3π(mc)2 0
E
−
E
−
E
A
B
γ
B
(max)
Z
Eγ
X |pBA |2 (EA − EB )
e2
2
=
dEγ
~c 3π(mc)2 0
EA − EB − Eγ
B
!
(max)
2
X
e
2
Eγ
.
|pBA |2 (EB − EA ) ln
=
2
~c 3π(mc) B
|EB − EA |
2
Bei
P dieser2 Herleitung wurde im ersten Schritt die Vollständigkeitsbeziehung (p )AA =
B |pBA | verwendet; im zweiten Schritt wurde für den Fall EB < EA die Singularität
bei Eγ = EB − EA behoben durch Ausschneiden eines kleinen symmetrischen Intervalls
(genaueres Studium des Grenzübergangs auf S. 41 zeigt, dass dies die korrekte Behandlung
ist); die Integrale über (0, EBA − η) und (EBA + η, 2EBA ) heben sich dann genau auf, und
(max)
das Endergebnis folgt nach Vernachlässigung von EAB relativ zu Eγ
∼ mc2 im Beitrag
der oberen Integrationsgrenze.
(obs)
Der erhaltene Ausdruck für ∆EA
ist für die Niveaus des Wasserstoffatoms
ohne
weiteres exakt auswertbar, weil sämtliche Eigenwerte EA und Eigenzustände |A exakt
bekannt sind. Die Summe erweist sich als konvergent; sie hängt natürlich noch logarithmisch
(max)
vom Abschneideparameter Eγ
ab. Zur näheren Auswertung schreiben wir das Ergebnis
in der Form
!
(max)
X
e2
2
Eγ
(obs)
∆EA =
ln
|pBA |2 (EB − EA ),
2
~c 3π(mc)
h|EB − EA |iav
B
was lediglich einer Definition von h|EB − EA |iav entspricht.
Als nächstes betrachten wir die Identität
pHat − Hat p = −i~∇V,
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
46
P
die für jedes Ein-Elektron-Atom gilt. Die zu berechnende Summe B |pBA |2 (EB − EA )
erhält man entweder durch Nehmen des (BA)-Matrixelements der Identität, Multiplikation
mit pAB und Summation über B, oder durch das ”gespiegelte” Verfahren:
X
X
X
|pBA |2 (EB − EA ) = −i~
pAB ·(∇V )BA = i~
(∇V )AB ·pBA .
B
B
B
Der ”Mittelwert” der zwei äquivalenten Ausdrücke liefert
X
B
|pBA |2 (EB − EA ) = −
i~
~2
([p, ∇V ])AA = − (∇2 V )AA .
2
2
Für das Coulombpotential gilt
∇2 V (r) = 4πe2 δ(r),
also
X
B
|pBA |2 (EB − EA ) = −2πe2 ~2 |ψA (0)|2 .
Diese Größe ist nur für s-Zustände nichtverschwindend; für diese gilt die Beziehung
|ψns (0)|2 =
1
πn3 a30
mit a0 =
~ ~c
.
mc e2
Für die Verschiebung der s-Niveaus des Wasserstoffatoms erhalten wir also letztendlich
!
2 3 2
(max)
E
8
e
e
1
γ
(obs)
∆Ens
ln
=
.
3
3π ~c 2a0 n
h|EB − EA |iav
Die Größe e2 /(2a0 ) ist die Rydbergenergie, die natürliche Einheit für atomare Energieabstände. Für Niveaus mit l 6= 0 erhalten wir in dieser Ordnung keine Energieverschiebung.
Eine numerische Rechnung liefert für h|EB − E2s |i den Wert 17,8 Ry. Einsetzen dieses
(max)
Wertes liefert für die Wahl Eγ
= mc2 die ”Vorhersage”
1
(obs)
(obs)
∆E2s − ∆E2p1/2 = 1040 M hz,
~
in erstaunlich guter Übereinstimmung mit dem experimentellen Wert 1060 M Hz. Ände(max)
rung von Eγ
um einen Faktor 2 würde eine Änderung der Vorhersage um etwa 9% mit
sich bringen. Die genaue Übereinstimmung ist also eher ein glücklicher Zufall, aber die
Größenordnung des Ergebnisses wird durch unsere sehr grobe Theorie recht gut vorhergesagt.
Die oben durchgeführte Rechnung hat also folgendes Ergebnis gebracht: Der nichtrelativistische Ausdruck für ∆EA ist in niedrigster Ordnung der Störungstheorie divergent
KAPITEL 2. QUANTENTHEORIE DES STRAHLUNGSFELDES
(max)
47
und hängt linear von der Abschneideenergie Eγ
ab; der Massenrenormierungsterm di(max)
vergiert auch linear mit Eγ
, aber die beobachtbare Niveauverschiebung ist nur noch
logarithmisch divergent. Die Abhängigkeit von der Abschneideenergie bedeutet, dass die
Rechnung eigentlich überhaupt keine quantitative Vorhersage gebracht hat! Andererseits
ist die Rechtfertigung für das Abschneiden der Integrale keineswegs problematisch: Die
nicht relativistische Rechnung reicht nun einmal für hohe Eγ nicht aus, und man weiß im
Prinzip, was man besser machen soll.
In der relativistischen Theorie sind, wie sich herausstellt, sowohl ∆EA als auch die
(max)
Massenrenormierung nur noch logarithmisch divergent mit Eγ
und für deren Differenz
(max)
erhält man einen endlichen, von Eγ
unabhängigen Wert. Es gibt in der relativistischen
Theorie noch einen zweiten Effekt, die Vakuumpolarisation. Wie wir in unserer Diskussion der Diracgleichung sehen werden, kann aus dem Vakuumzustand vorübergehend ein
Elektron-Positron-Paar entstehen, das wegen Nichterhaltung der Energie natürlich wieder
schnell verschwinden muss. Während der kurzen Existenz des Paares werden die beiden
aber durch ein etwaiges äußeres Feld ein wenig auseinander gezogen, was zu einer Abschirmung sämtlicher Ladungen führt, genau wie für eine Ladung in einem Dielektrikum. Diese
sogenannte Ladungsrenormierung ist wieder formal divergent, aber prinzipiell unbeobachtbar. Im Wasserstoffatom gibt es aber beobachtbare Effekte, weil sowohl Elektron als
auch Proton in die ”Abschirmungswolke” aus Vakuumfluktuationen des jeweilig anderen
Teilchens kommen. Dieser Nettoeffekt ist wieder endlich, und die Summe der beiden so
(obs)
berechneten Beiträge zu ∆EA
stimmt innerhalb der inzwischen sehr kleinen Messungenauigkeiten mit dem Experiment überein. Die einschlägigen Rechnungen wurden in den
vierziger Jahren von Tomonaga, Schwinger und Feynman unabhängig voneinander durchgeführt. Der Beweis, dass die entwickelten Formalismen auch in höheren Ordnungen endliche
Ergebnisse liefern, stammt von Dyson. Um diese Übereinstimmung zu erhalten, müssen
auch Terme höherer Ordnung in der Störungstheorie betrachtet werden, aber bei diesen
treten keine neuen Divergenzen auf. Eine Theorie, in der nur endlich viele divergente
Graphen auftreten, heißt renormierbar.
Während die relativistische Quantenelektrodynamik also quantitativ sehr genaue Vorhersagen machen kann, wird die Rechtfertigung der formalen Vorgehensweise um einiges
diffiziler: Das Auftreten divergenter Ausdrücke für Massen- und Ladungsrenormierung ist
ein Indiz dafür, dass auch die relativistische Theorie im Bereich extrem hoher Energien
nicht korrekt sein kann. Es ist aber noch nicht klar, welche neuen physikalischen Effekte
die Massen- und Ladungsrenormierung zustande bringen (Effekte der Gravitation, Supersymmetrie, Superstrings, . . . ). Der wesentliche Vorteil einer renormierbaren Theorie ist
aber, dass man die Antwort auf diese Frage nicht zu wissen braucht, um mit der Theorie
selbst weiterarbeiten zu können. Viele Physiker halten sogar das ”Problem der Behebung
der Divergenzen” eher für ein psychologisches Problem der Theoretiker. In dieser Betrachtungsweise reicht es völlig aus, dass ein wohldefinierter Algorithmus zur Berechnung sämtlicher beobachtbarer Effekte existiert, und es wird als eine Anmaßung empfunden, der Natur
vorzuschreiben, welcher Art von Mathematik sie sich zu bedienen hat.
Kapitel 3
Quantentheorie von Fermionfeldern
3.1
Hilbertraum und Feldoperatoren für
identische Fermionen
In diesem Kapitel werden wir auch für Fermionen einen Besetzungszahlformalismus
entwickeln, der demjenigen für Photonen möglichst analog ist. Als erstes brauchen wir dazu
einen Satz von Modenfunktionen. Diese können ziemlich willkürlich gewählt werden;
die einzige Bedingung ist, dass sie vollständig sein müssen. Eine mögliche Wahl sind die
stationären Zustände irgendeines Referenz-Hamiltonoperators Href ,
Href φk (r, sz ) = Ek φk (r, sz )
mit
Href =
p2
+ Vref (r)
2m
und der Normierung
XZ
dr |φk (r, sz )|2 = 1.
sz
Weil Fermionen immer einen Spin haben, haben wir auch den Spinfreiheitsgrad explizit angegeben. In der obigen Definition ist Vref spinunabhängig gewählt; eine Verallgemeinerung
auf spinabhängige Potentiale bereitet keine Schwierigkeiten, wird aber für unsere Zwecke
nicht gebraucht. Unsere Wahl impliziert, dass jeder Eigenwert mindenstens (2s + 1)-fach
entartet ist; diese Entartung muss natürlich beim Abzählen der Eigenzustände berücksichtigt werden.
Als Basiszustände
des Hilbertraumes wählen wir wieder die Besetzungszahl-Eigen
zustände |{nk } , wobei jetzt aber die nk nur dieP
Werte 0 und 1 annehmen können (Pauliverbot!). Weiters gilt wieder die Nebenbedingung k nk < ∞. In Folge führen wir Erzeuger
c†k und Vernichter ck ein, die die Besetzungszahl nk um eins erhöhen bzw. erniedrigen, falls
dies erlaubt ist. Diese Vorschrift legt die ck und c†k noch nicht fest; die allgemeinste noch
zugelassene Form, für die ck und c†k hermitesch konjugiert sind, ist
c†k |{nl } = [1 − nk ]eiφk ({nl +δkl }) |{nl + δkl }
(1.1)
ck |{nl } = nk e−iφk ({nl }) |{nl − δkl } ,
48
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
49
wobei die Phasen φk ({nl }) im Prinzip noch frei wählbar sind. Insbesondere könnte man
sie alle, wie im analogen Bose-Fall, gleich Null wählen; dies führt aber zu einem recht
schwerfälligen Formalismus. Um zur Festlegung der φk ({nl }) zu gelangen, betrachten wir
zuerst die Identität
†
†
ck ck + ck ck |{nl } = (1 − nk + nk )|{nl } = |{nl } ,
oder
n
o
c†k , ck ≡ c†k ck + ck c†k = 1.
Statt einer charakteristischen Vertauschungsbeziehung, wie für Bosonen, haben wir also
hier eine charakteristische Antivertauschungsbeziehung. Es liegt jetzt nahe, diese Antikommutatorstruktur auszubauen und zu fordern
o
n
o
n
(1.2)
c†k , cl = δkl ;
c†k , c†l = {ck , cl } = 0.
Dies wird ermöglicht durch die von Jordan und Wigner vorgeschlagene Phasenkonvention
X
φk ({nl }) = π
nl0 ;
l0 <k
für diese Konvention ist es also notwendig, die Indizes k auf irgendeine, weitgehend willkürliche, aber ein für allemal festzulegende, Weise zu ordnen. Der formale Beweis, dass
diese Vorschrift nach Substitution in (1.1) zu den Beziehungen (1.2) führt, ist nicht sehr
schwierig, aber etwas mühsam, und wir beschränken uns auf einige Beispiele:
c†1 c†2 |{0} = c†1 |01 ; 12 = |11 ; 12 ;
c†2 c†1 |{0} = c†2 |11 ; 02 = −|11 ; 12 ;
c†1 c3 |01 ; 12 ; 13 = −c†1 |01 ; 12 ; 03 = −|11 ; 12 ; 03 ;
c3 c†1 |01 ; 12 ; 13 = c3 |11 ; 12 ; 13 = |11 ; 12 ; 03 .
Wir bemerken noch nebenbei, dass der Operator
Nk = c†k ck
der Zähloperator für die Zahl der Fermionen im Zustand φk (r, sz ) ist:
Nk |{nl } = nk |{nl } .
Der Operator
X
N=
Nk
k
ist offensichtlich der Operator für die Gesamtzahl der Fermionen.
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
3.1.1
50
Feldoperatoren
Wir führen jetzt den Feldoperator ψ(r, sz ) ein mittels
X
ψ(r, sz ) =
ck φk (r, sz )
k
und betrachten den Kommutator
h
i
X
[N, ψ(r, sz )] =
φl (r, sz ) c†k ck , cl .
k,l
Aus der Beziehung
h
i
n
o
†
†
†
†
†
†
ck ck , cl = ck ck cl − cl ck ck = ck ck cl + ck cl ck − ck , cl ck
= c†k ck cl + c†k cl ck − δkl ck = −δkl ck
folgt
[N, ψ(r, sz )] = −ψ(r, sz ),
also der Operator ψ(r, sz ) erniedrigt die Fermionenzahl um eins. Aufgrund der Identität
ψ(r, sz )|{δlk } = φk (r, sz )|{0} ,
gilt zusätzlich noch, dass ψ(r, sz ) nur ein Fermion vernichten kann, falls eines am Ort r
mit Spin sz vorhanden ist. Auf ähnliche Weise kann man den adjungierten Operator
X †
ψ † (r, sz ) =
ck φ∗k (r, sz )
k
interpretieren als den Erzeuger eines Fermions mit Spin sz am Ort r. Aufgrund der Vollständigkeit der φk (r, sz ) gilt die Antikommutatorbeziehung
n
o
†
X ∗
ψ (r, sz ), ψ(r0 , s0z ) =
φk (r, sz )φl (r0 , s0z ) c†k , cl
k,l
=
X
k
φ∗k (r, sz )φk (r0 , s0z ) = δ(r − r0 )δsz s0z .
Es liegt jetzt nahe, den Operator
ρ(r, sz ) = ψ † (r, sz )ψ(r, sz )
als die Teilchendichte am Ort r für den Spin sz zu interpretieren. Aufgrund der Orthonormalität der φk gilt
XZ
XXXZ
†
drψ (r, sz )ψ(r, sz ) =
drc†k cl φ∗k (r, sz )φl (r, sz )
sz
sz
=
k
XX
k
l
l
δkl c†k cl =
X
c†k ck = N,
k
also die integrierte Teilchendichte liefert die Teilchenzahl, wie es sich gehört.
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
51
Bemerkung
Bei der obigen Formulierung ist es eher nebensächlich, dass wir die Modenfunktionen in
der (r, sz )-Darstellung spezifiziert haben. Man erhält einen völlig äquivalenten Formalismus
mit ψ † (p, sz ) und ψ(p, sz ), falls man statt dessen die (p, sz )-Darstellung wählt.
Als nächstes betrachten wir die Paardichte, d.h. den Operator, dessen Erwartungswert
die Wahrscheinlichkeit dafür angibt, dass sich sowohl am Ort r ein Teilchen mit Spin sz
als auch am Ort r0 ein Teilchen mit Spin s0z befindet. Dieser Operator ist
1
ρ2 (x0 , x) = ψ † (x0 )ψ † (x)ψ(x)ψ(x0 ),
2
wobei wir die kompakte Notation x für das Paar (r, sz ) eingeführt haben. (Eine Integration über x wird im folgenden auch immer als Integration über r und Summation über sz
aufzufassen sein.) Wir berechnen als Beispiel den Erwartungswert von ρ2 (x0 , x) im Zweiteilchenzustand |1k , 1l :
0
1k , 1l |ρ2 (x , x)|1k , 1l
2
1 0 † †
= {0}|ψ(x)ψ(x )ck cl |{0} 2
2
1 †
†
0 †
0
= − {0}|ψ(x)ck ψ(x )cl |{0} + φk (x ) {0}|ψ(x)cl |{0} 2
1
2
= |−φk (x)φl (x0 ) + φk (x0 )φl (x)| .
2
Wir erhalten also das Betragsquadrat einer antisymmetrisierten Zwei-Teilchen-Wellenfunktion. Die Normierungsbedingung lautet
Z
Z
dx dx0 1k , 1l |ρ2 (x0 , x)|1k , 1l = 1.
wie aus der Orthonormalität der Modenfunktionen φk leicht hergeleitet werden kann. Für
einen n-Teilchen-Zustand erhält man auf ähnliche Weise
Z
Z
n
0
0
dx dx n|ρ2 (x , x)|n =
.
2
also die Zahl der Paare, die aus den Modenindizes gebildet werden können.
3.1.2
Der Hamiltonoperator für Fermionfelder
Wir betrachten jetzt ein System aus identischen Teilchen, die sich in einem gemeinsamen
äußeren Potential V (r) bewegen und weiters eine Paarwechselwirkung W (ri − rj ) miteinander haben.
Für den Erwartungswert der potentiellen Energie erhält man so in einem
Zustand |χ den Ausdruck
Z
Z
Z
χ|Hpot |χ = dx V (r) χ|ρ(x)|χ + dx dx0 W (r − r0 ) χ|ρ2 (x, x0 )|χ .
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
52
Die kinetische Energie hat eine entsprechend einfache Form in der Impulsdarstellung:
Z
X
p2 χ|Hkin |χ =
dp
χ|ψ † (p, sz )ψ(p, sz )|χ .
2m
s
z
Weil ψ(p, sz ), wie in der normalen Quantentheorie, als Fouriertransformierte von ψ(r, sz )
geschrieben werden kann, lässt sich dies umformen zu
Z
X
~2 2
†
χ|Hkin |χ =
dr χ|ψ (r, sz ) −
∇ ψ(r, sz )|χ .
2m
s
z
Für den gesamten Hamiltonoperator erhalten wir also
Z
~2 2
†
H = dx ψ (x) −
∇ + V (r) ψ(x)
2m
Z
Z
1
+
dx dx0 ψ † (x0 )ψ † (x)W (r − r0 )ψ(x)ψ(x0 ).
2
(1.3)
Verallgemeinerungen, die spinabhängige Wechselwirkungen und/oder Mehrteilchenwechselwirkungen enthalten, sind leicht hinzuschreiben, aber für uns nicht weiters von Interesse.
3.2
Die Hartree-Fock-Näherung
Eine der Aufgaben der Atom-, Kern- und Festkörperphysik ist es, die stationären Zustände
des Hamiltonoperators (1.3) für ein n-Teilchen-System zu bestimmen. Um eine Idee für die
dabei auftretenden Schwierigkeiten zu erhalten, leiten wir zuerst die Bewegungsgleichung
für den Feldoperator ψ(x) , betrachtet als ein Operator im Heisenbergbild, ab. Insbesondere
betrachten wir den Kommutator
[H, ψ(x)] = [H0 + Hw , ψ(x)] ,
wobei H0 den Ein-Teilchen-Anteil und Hw den Wechselwirkungsanteil bezeichnet:
Z
H0 = dx0 ψ † (x0 )H10 ψ(x0 )
mit
~2 02
∇ + V (r0 ).
2m
Für den ersten Teil des Kommutators erhalten wir so
Z
[H0 , ψ(x)] = dx0 ψ † (x0 )H10 ψ(x0 ), ψ(x)
Z
= dx0 −ψ † (x0 )ψ(x)H10 ψ(x0 ) − ψ(x)ψ † (x0 )H10 ψ(x0 )
Z
= − dx0 δ(x − x0 )H10 ψ(x0 ) = −H1 ψ(x).
H10 = −
53
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
Bei dieser Herleitung wurde im ersten Schritt das ”Antivertauschen” von ψ(x) mit ψ(x0 ),
sowie das Vertauschen von H10 und ψ(x) ausgenutzt (H10 wirkt auf x0 , aber nicht auf x). Im
zweiten Schritt wurde der Antikommutator von ψ † (x0 ) und ψ(x) eingesetzt. Das Ergebnis
ist nicht sonderbar aufregend; ohne Wechselwirkung erhält man ψ(x, t) dadurch, dass man
ψ(x) entwickelt nach den Eigenfunktionen φ̃l (x) von H1 mit Eigenwerten Ẽk ,
X
ψ(x) =
c̃l φ̃l (x),
l
und dann jedem c̃l seinen Zeitfaktor gibt:
X
i
ψ(x, t) =
c̃l φ̃l (x)e− ~ Ẽl t .
l
Der Kommutator mit dem Wechselwirkungsterm ergibt
Z
Z
1
0
[Hw , ψ(x)] =
dx
dx00 ψ † (x0 )ψ † (x00 )W (r0 − r00 )ψ(x00 )ψ(x0 ), ψ(x)
2
Z
Z
1
0
=
dx
dx00 W (r0 − r00 ) ψ † (x0 ) ψ(x), ψ † (x00 ) ψ(x00 )ψ(x0 )−
2
δ(x − x0 )ψ † (x00 )ψ(x00 )ψ(x0 )
1
=
2
Z
=−
Z
dx0 W (r0 − r)ψ † (x0 )ψ(x)ψ(x0 )−
Z
00
00
†
00
00
dx W (r − r )ψ (x )ψ(x )ψ(x)
dx0 W (r0 − r)ψ † (x0 )ψ(x0 )ψ(x).
Die Wechselwirkung verknüpft also die Zeitentwicklung des Feldoperators ψ(x) mit derjenigen eines Produktes aus drei Feldoperatoren. Die Bestimmung der Zeitentwicklung dieser
letzteren Größe erfordert Kenntnisse über Produkte aus 5 Feldoperatoren usw. Es bestehen also kaum Aussichten, ohne recht drastische Näherungen irgendwelchen Fortschritt zu
machen.
Die auf Hartree und Fock zurückgehende Idee zur Erhaltung einer Näherungslösung
ist jetzt folgende:
1) Man nehme an, es existiert ein Satz von n Basisfunktionen φl (x), welche näherungsweise harmonisch von der Zeit abhängen (als Heisenbergbild-Operatoren betrachtet).
Für die Entwicklungskoeffizienten von ψ(x, t) nach diesen speziellen Basisfunktionen
soll also gelten
i
cl (t) = e− ~ l t cl
(2.1)
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
54
2) Nehme in dem Ausdruck
Z
[Hw , ψ(x)] = − dx0 W (r0 − r)ψ † (x0 , t)ψ(x0 , t)ψ(x, t)
Z
X †
=−
ck (t)cl (t)cm (t) dx0 W (r0 − r)φ∗k (x0 )φl (x0 )φm (x)
k,l,m
nur diejenigen Terme mit, die mit irgendeiner der in ψ(x, t) schon vorkommenden Frequenzen resonant sind. Dies sind sicher die wichtigsten Terme; der Effekt der sonstigen Terme wird sich bei der Ausintegration der Bewegungsgleichungen weitgehend
ausmitteln. Nach dieser Näherung bleiben (in Abwesenheit zufälliger Entartungen)
nur noch die Terme mit k = l oder k = m übrig.
3) Ersetze in den übriggebliebenen Termen den Operator c†k ck durch seinen Erwartungswert hnk i im gesuchten stationären n-Teilchenzustand. Man erhält so
Z
X
hnk i cm (t) dx0 W (r0 − r)φ∗k (x0 )φk (x0 )φm (x)
[Hw , ψ(x, t)] = −
k,m
+
X
k,l
=−
hnk i cl (t)
Z
dx0 W (r0 − r)φ∗k (x0 )φk (x)φl (x0 )
Z
dx0 W (r0 − r) ψ † (x0 )ψ(x0 ) ψ(x)
Z
+ dx0 ψ(x0 )W (r0 − r) ψ † (x0 )ψ(x) ,
wobei wir die Summen für ψ(y) und ψ † (y) zurückgebildet haben, und benutzt haben,
dass in einem stationären Zustand im Rahmen der Näherung (2.1) gelten muss
D
E
c†k cl = δkl hnk i .
Wenn wir jetzt den Ausdruck für [Hw , ψ(x, t)] bilden und nach den (immer noch gesuchten) φl (x) zerlegen, und weiters die Bedingung (2.1) einsetzen, erhalten wir die Eigenwertgleichung
Z
† 0
0
0
0
l φl (x) = H1 + dx W (r − r) ψ (x )ψ(x ) φl (x)
Z
− dx0 φl (x0 )W (r0 − r) ψ † (x0 )ψ(x) ,
oder
Z
l φl (x) = H1 +
−
Z
!
0
0
dx W (r − r)
X
dx0 φl (x0 )W (r0 − r)
k
hnk i φ∗k (x0 )φk (x0 )
X
k
hnk i φ∗k (x0 )φk (x).
φl (x)
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
55
Es treten also zu H0 zwei zusätzliche Terme auf: ein von der gemittelten Teilchendichte erzeugtes direktes Wechselwirkungspotential und ein zusätzliches, nichtlokales Austauschpotential. Zum letzteren tragen nur dieRZustände bei, die denselben Spin wie das gesuchte
φl (x) [d.h. φl (r, sz )] haben; das Symbol dx0 bedeutet auch eine Summation über s0z , und
wenn φl (x0 ) und φm (x) bezüglich ihrer Spinabhängigkeit zueinander orthogonal stehen,
trägt der Term l = m zum Austauschpotential nicht bei.
Die oben hergeleiteten Gleichungen heißen Hartree-Fock Gleichungen. Sie sind nichtlinear und implizit; die gesuchten Funktionen φl (x0 ) kommen auch an der rechten Seite
vor, und die Gleichungen müssen selbstkonsistent gelöst werden. In der Praxis geht man
iterativ vor: Man nimmt zuerst n einigermaßen plausibel erscheinende Versuchsfunktionen
φ0k (x), setzt die zugehörigen hnk i gleich eins und berechnet direktes und Austauschpotential. Als nächstes löst man das so entstandene lineare Eigenwertproblem und nimmt die
n Lösungen mit niedrigstem l als neue Versuchsfunktionen φ1k (x). Man wiederholt dieses
Verfahren, bis sich die φik (x) von den φi−1
k (x) nicht mehr nennenswert unterscheiden. In
der Praxis konvergiert das Verfahren recht ordentlich. Es ist aber nicht gesichert, dass die
Lösung eindeutig (d.h. von der Wahl der φ0k unabhängig) ist; man kennt Beispiele, in denen
es mehrere Lösungen gibt.
Bemerkung 1
Durch Weglassen des Austauschtermes erhält man aus den Hartree-Fock-Gleichungen die
sog. Hartree-Gleichungen. Dabei lässt man allerdings den Term k = l im direkten Potential (der im Hartree-Fock-Formalismus vom entsprechenden Term im Austauschpotential
genau kompensiert wird) weg. Historisch wurden die Hartree-Gleichungen zuerst hergeleitet; man erhält sie, wenn man zu den vorhergehenden ähnliche Betrachtungen durchführt
in der ”normalen” n-Teilchen-Quantenmechanik unter Berücksichtigung des Pauliverbotes, aber ohne Antisymmetrisierung der Wellenfunktion. Hartree zeigte, dass man zu den
Hartree-Gleichungen geführt wird, falls man mit Hilfe der Variationsrechnung versucht,
den Erwartungswert des Hamiltonoperators
H=
n
X
(i)
H1 +
i=1
n
1 X
W (ri − rj )
2 i6=j=1
innerhalb der Klasse der Versuchswellenfunktionen vom Typ
φ(x1 , . . . , xn ) =
n
Y
φi (xi )
i=1
zu minimieren, wobei die {φi } einen Satz orthonormaler Funktionen bilden. (Im obigen
(i)
Ausdruck bezeichnet H1 den Operator H1 wirkend auf die Variablen des i-ten Teilchens).
Die Hartree-Fock-Gleichungen erhält man auf ähnliche Weise durch Minimierung innerhalb
der Klasse von antisymmetrisierten Produktwellenfunktionen (oder Slaterdeterminan-
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
56
ten)
n
Y
1 X
p
√
(−1)
φi (xpi ),
φ(x1 , . . . , xn ) =
n! p
i=1
wobei über alle Permutationen P der Indizes 1 bis n summiert wird.
Bemerkung 2
Der wichtigste Mangel der Hartree-Fock-Zustände ist die völlig unzureichende Beschreibung der Korrelationen in den Positionen der Elektronen. Für die Zweiteilchendichte im
Hartree-Fock-Grundzustand gilt
X
0 0
ρ2 (r, sz ; r , sz ) =
φ∗k (r, sz )φk (r, sz )φ∗l (r0 , s0z )φl (r0 , s0z )
k<l
− φ∗k (r, sz )φk (r0 , s0z )φ∗l (r0 , s0z )φl (r, sz ) .
Falls sz 6= s0z gibt der zweite Term keinen Beitrag (dies ist sofort klar, wenn die {φl }
Eigenfunktionen von sz sind; aber auch sonst ist dies leicht zu zeigen), und man erhält z.B.
1
1
1
1
ρ2 (r, + ; r0 , − ) = ρ(r, + )ρ(r0 , − ),
2
2
2
2
ein für ein System mit Coulombabstoßung völlig unrealistisches Ergebnis. Für sz = s0z
erhält man schon Korrelationen; insbesondere gilt auch im Hartree-Fock-Grundzustand
ρ2 (r, sz ; r, sz ) = 0,
wie es aufgrund des Pauliverbots sein soll, aber sonst ist auch hier das Hartree-FockErgebnis für die Korrelationsfunktion
g2 (x, x0 ) ≡ ρ2 (x, x0 ) − ρ(x)ρ(x0 )
weit von der Realität entfernt. Die Berechnung von Korrelationseffekten ist wegen der
langen Reichweite des Coulombpotentials recht diffizil; eine ”normale” Störungsentwicklung um das Hartree-Fock-Ergebnis konvergiert schlecht und führt für ausgedehnte Systeme (Festkörper) sogar zu Divergenzen oder unphysikalischen Formabhängigkeiten in den
einzelnen Ordnungen. Erst eine Resummation der Störungsreihe, die dem Phänomen der
Abschirmung der Coulombkräfte Rechnung trägt, führt zu einigermaßen akzeptablen Ergebnissen (siehe Kap. 6 im Buch von Kittel für eine Einführung in die Problematik). Die
Korrelationsfunktion kann insbesondere durch Streuung polarisierter Neutronen gemessen
werden; Experimente dieser Art wurden in letzter Zeit am Hochflussreaktor in Grenoble
an einigen Materialien durchgeführt.
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
3.2.1
57
Die Bedeutung der Hartree-Fock Eigenwerte
Die Hartree-Fock Eigenwertgleichung besitzt viele der Eigenschaften einer normalen Schrödingergleichung; insbesondere kann sie geschrieben werden als
1
φl (x),
l φl (x) = HHF
1
wobei HHF
ein effektiver hermitescher Ein-Teilchen-Hamiltonoperator ist, der zwar von
dem gesuchten Vielteilchenzustand, aber nicht vom Modenindex l abhängt. (Wegen
des Weglassens des Terms k = l ist dies in der Hartree-Näherung nicht der Fall!) Letztere
Unabhängigkeit bringt mit sich, dass der übliche Beweis der Orthogonalität der φl mit
unterschiedlichen l ohne weiteres auch auf die Hartree-Fock Eigenfunktionen anwendbar
ist; es ist also möglich, die φl (x) orthonormal zu wählen. Andererseits gilt nicht, dass die
Hartree-Fock Grundzustandsenergie geschrieben werden kann als Summe der l für die
besetzten Ein-Teilchen-Zustände:
E0,HF 6=
n
X
(2.2)
l .
l=1
Zur Überprüfung der obigen Ungleichheit berechnen wir zuerst einen Ausdruck für l
durch Multiplikation der Eigenwertgleichung mit φ∗l (x) und Integration über x:
Z
l =
dx
φ∗l (x)H1 φl (x)
+
n Z
X
k=1
−
n Z
X
k=1
Z
dx
Z
dx
dx0 |φl (x)|2 W (r − r0 )|φk (x0 )|2
dx0 φ∗l (x)φ∗k (x0 )W (r − r0 )φl (x0 )φk (x).
Andererseits erhält man für den Erwartungswert des Vielteilchen-Hamiltonoperators
(1.3)
im Hartree-Fock-Grundzustand |11 , . . . , 1n ; 0n+1 , . . . ≡ |0HF das Ergebnis
Z
X
E0,HF = 0HF |H|0HF =
dx φ∗l (x)H1 φl (x)
l
Z
n
n Z
1 XX
dx dx0 |φk (x)|2 W (r − r0 )|φl (x0 )|2
+
2 k=1 l=1
Z
n
n Z
1 XX
−
dx dx0 φ∗l (x)φ∗k (x0 )W (r − r0 )φl (x0 )φk (x).
2 k=1 l=1
Die Wechseiwirkungsterme treten also in den zwei in (2.2) verglichenen Ausdrücken mit
unterschiedlichen Vorfaktoren auf. Die Energien l − l0 (l0 ≤ n, l > n) sind genau die
Energien, die man brauchen würde, um ein Elektron aus dem Zustand l0 in den Zustand
l zu bringen ohne Änderung der Zustände der sonstigen Elektronen. Für große
Atome und Kerne (und erst recht für Festkörper) kann die Änderung der Zustände der
58
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
verbliebenen Elektronen (Konfigurationsrelaxation) vernachlässigt werden, und die l − l0
können dann mit den experimentellen Anregungsenergien für Elektronen verglichen werden. Als Beispiel der so erhaltenen Ergebnisse werden in der nachfolgenden Tabelle die mit
der Hartree-Fock-Näherung errechneten lonisationsenergien für die verschiedenen Zustände
mit dem Experiment verglichen. Dabei ist zu berücksichtigen, dass die L·S-Kopplung in
der Rechnung nicht berücksichtigt wurde, im Experiment aber nicht abzuschalten ist.
1s
1828
HF
exp
n
Fehler
j = l + 1/2
j = l − 1/2
2s
270
2p
3s
3p
3d
251
52,2
44,3
29,8
260,1
46,0
27,8
1879,7 282,0
53,4
247,2
43,6
27,4
−2,8% −4,4% −1,1% −2,3% −1,1% +7,4%
4d
1,69
1,57
+7,1%
(Energien in Rydberg.) Für Näheres siehe Bethe-Jackiw.
Zwischenbemerkung: Die Symmetrie der Orbitale
In der obigen Tabelle wurden die Funktionen φl (x) (weiters auch Orbitale genannt) charakterisiert durch Quantenzahlen, wie sie für ein Zentralfeldproblem üblich sind. Genau betrachtet ist aber das effektive Potential nicht exakt zentralsymmetrisch, außer für ein Atom
mit abgeschlossenen Schalen (Edelgasekonfiguration); im letzteren Fall ist sofort klar, dass
das direkte Potential zentralsymmetrisch ist, und eine relativ mühsame Rechnung zeigt,
dass auch das Austauschpotential eine so symmetrische Form hat, dass Lösungen vom Typ
φk (x) = φnlmσ (r, sz ) =
Rnl (r)
Ylm (θ, φ)χσ (sz )
r
möglich sind (siehe Bethe-Jackiw, S.64, für Einzelheiten). Für nicht-Edelgas-Atome ist die
obige Überlegung nicht mehr exakt gültig; sie bleibt aber aufrecht für den Beitrag ge1
, und für die sonstigen Beiträge erweist es sich als eine nicht
schlossener Schalen zu HHF
zu schlechte Näherung, auch diese durch ihr Mittel über die Winkel zu ersetzen; die so
gemachten Fehler sind klein gegenüber den ohnehin schon in der Hartree-Fock-Näherung
enthaltenen. Die sphärische Mittelung bringt einen zweifachen Vorteil: Erstens sind die
Rechnungen um Größenordnungen einfacher, weil eindimensionale statt dreidimensionale gekoppelte Integro-Differentialgleichungen selbstkonsistent zu lösen sind. Zweitens sind
auch die Ergebnisse einfacher zu deuten, und insbesondere lässt sich das Periodensystem
relativ leicht anhand eines Hartree-Fock Schalenbildes diskutieren.
Ähnliche Überlegungen können für Festkörper gemacht werden. Das effektive Potential
V (r), das in der Theorie der Bandstruktur von Festkörpern auftritt, soll eigentlich auch
als selbstkonsistentes Potential im Sinne einer Hartree-Fock-Theorie aufgefasst werden.
Auch hier kann nur für die Beiträge vollständig gefüllter Bände gezeigt werden, dass sie
strenge Gitterperiodizität besitzen. Die Beiträge teilweise gefüllter Bände brauchen nicht
die Symmetrie des Gitterpotentials zu haben (Gegenbeispiel: Für von Leitungselektronen
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
59
verursachten Ferromagnetismus ist das effektive Potential, im Gegensatz zum Gitterpotential, spinabhängig). In ”normalen” Materialien stellt der Ansatz einer Bloch-Form für die
Orbitale:
φl (x) = eik·r ukn (r)χσ (sz ),
mit gitterperiodischem ukn (r), noch eine der harmlosesten Näherungen in einer Bandstrukturrechnung dar. Insbesondere bei genau halbgefüllten Bändern muss man aber auf
das Auftreten von Strukturen mit dem inversen Fermi-Wellenvektor (Elektrondichtewellen)
gefasst sein. Solche Strukturen in der Elektronendichte führen aber i.a. wieder zu Gitterverzerrungen, womit dann wieder Gitter und Elektronen ”in Gleichschritt” gebracht worden
sind.
3.2.2
Beispiel: Das Elektronengas
Ein einfaches Beispiel, wofür die Hartree- und Hartree-Fock-Gleichungen exakt gelöst werden können, ist das Elektronengas, d.h. ein Modell, in dem das Potential der lonenrümpfe
ersetzt wird durch das Potential einer homogenen über das Kristallvolumen ausgeschmier(+)
ten Ladungsverteilung ρ0 = N |e|/V . Die Hartree-Gleichung lautet dann
#
"
Z
Z
n 0
(+)
2
X
|e|
ρ
e
p2
− dx0 0 0 + dx0
φ∗ (x0 )φk (x0 ) φl (x),
l φl (x) =
2m
|r − r |
|r − r0 | k=1 k
wobei der Strich bei der Summation bedeutet, dass der Term k = l entfällt. Wir versuchen
den Lösungsansatz
1
φkσ (r, sz ) = √ eik·r χσ (sz ),
V
wobei der Wellenvektor k so gewählt werden soll, dass die periodischen Randbedingungen
an den Grenzen des kubisch gewählten Volumens erfüllt sind. Mit dieser Wahl erhält man
für die Ladungsdichte im direkten Potential
0
N
X0
X
N −1
1
(−)
∗
e
e=
e.
φk (r)φk (r) = eρ0 =
V
V
k
k=1
Bis auf einen Fehler der Ordnung 10−23 hebt also das direkte Potential das äußere Potential
der verschmierten Rumpfladungen genau auf, und man erhält für die Hartree-Energien
genau die Werte für freie Teilchen
~2 k2
.
2m
Im Grundzustand sind sämtliche k-Werte bis zu einem Wert kF mit jeweils zwei Elektronen
(zwei Spinrichtungen) besetzt. kF bestimmt man aus der Beziehung
r
Z kF
Z
V
V
1
N
3
2 3
k 2 dk dΩ = 2 kF3 = N −→ kF = 3π 2 .
8π 0
π 3
V
kσ =
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
Für die mittlere Energie pro Teilchen
R
3 ~2 kF2
~2 k 2 k 2 dk
R
=
=
hl i =
2m
5 2m
k 2 dk
60
erhält man
3
F ,
5
wobei auch F wieder in der Dichte auszudrücken ist. Oft wählt man eine etwas andere
Darstellung und drückt kF aus in dem Radius r0 des mittleren Volumens pro Teilchen:
r
V
4 3
1
4
3
πr0 =
−→ kF =
mit α0 =
= 0,521 . . . .
3
N
α0 r0
9π
Ein vernünftiger dimensionsloser Parameter ist das Verhältnis rs von r0 zum Bohr’schen
Radius a0 = ~2 /(me2 ) = 0,529 Å. Ausgedrückt in diesem Parameter erhält man
hl i =
3 me4 1
2,210
=
Ry.
2
5 2~2 α0 rs2
rs2
Zwischenbemerkung
Der obige Ausdruck ist nicht mit der Energie pro Teilchen im Hartree-Grundzustand identisch. Bei der Berechnung der letzteren Größe geht die Wechselwirkung der Elektronen mit
dem Hintergrund voll ein, die Wechselwirkung der Elektronen untereinander aber nur mit
dem Faktor 1/2. Die physikalisch interessante Größe ist aber nicht diese Grundzustandsenergie, sondern die Kohäsionsenergie in der auch noch die elektrostatische Energie der
Hintergrundladung in Betracht gezogen wird. Letztere ist wieder genau gleich der Wechselwirkungsenergie der Elektronen und die Bilanz stimmt wieder! Man kann dieses Ergebnis
auch dadurch erreichen, dass man das Elektronengas so aufbaut, dass man abwechselnd ein
Elektron in das Volumen V hineinbringt und den positiven Hintergrund um eine Einheitsladung aufstockt. Weil man so immer Ladungen an fast-neutralen Systemen hinzufügt,
braucht man (bis zu Ordnung N −1 ) keine elektrostatische Arbeit zu leisten.
3.2.3
Die Austauschenergie des Elektronengases
Es wird sich jetzt herausstellen, dass die ebenen Wellen auch Eigenfunktionen des Austauschterms in der Hartree-Fock Eigenwertgleichung sind. Da die Austauschkräfte nur
zwischen Orbitalen gleicher Spins wirken, gilt
X 0 1 Z
1 ik·r ~2 k2 1 ik·r
0
0
0
√ e −
√
=
dr0 ei(k−k )·r W (r − r0 )eik ·r
kσ √ e
3
2m V
V
V
|k0 |<kF
Z
X 0 1
0
0
√
= ... −
dr0 ei(k−k )·(r −r) W (r − r0 )eik·r ,
V3
|k0 |<kF
und durch Übergehen auf die Integrationsvariable r0 − r = s erhält man
~2 k2
1 X0
kσ =
−
G(k − k0 ),
2m
V k0 <k
F
61
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
wobei G(q) für das Coulombpotential den Wert
Z
Z
e−iq·s
4πe2
−iq·s
2
G(q) = ds e
W (s) = e
ds
= 2
s
q
annimmt. Substitution dieses Ausdruckes ergibt
Z
4πe2 X 0
1
~2 k2
4πe2 V
=−
kσ −
=−
2m
V k0 <k |k − k0 |2
V 8π 3
F
2
Z
kF
k<kF
Z
dk0
1
|k − k0 |2
+1
e
1
dµ 2
2π
k 02 dk 0
2
02
2π
k + k − 2kk 0 µ
−1
0
Z
e2 kF 0 0
e2 kF2 − k 2 kF + k k + k0
=−
=−
ln k dk ln
+ kF .
πk 0
|k − k 0 |
π
2k
kF − k =−
Im Punkt k = kF hat die Funktion kσ eine senkrechte Tangente: für k = kF (1 + x) gilt
2
~2 k2 e2 kF
2
−
1 + x ln
+ O(x ) .
kσ =
2m
π
|x|
ΡHΕL
ΕF
Ε
−1
Weil die Zustandsdichte einen Faktor ∂∂kkσ
enthält (die erlaubten k-Werte sind im
k-Raum gleichmäßig verteilt), bedeutet dies eine verschwindende Zustandsdichte an der
Fermikante, was für die Transporteigenschaften bei niedriger Temperatur und für das thermodynamische Verhalten bedeutsam wäre. Allerdings ist die Einschneidung in der Zustandsdichte sehr schmal (siehe Skizze): um auf einen Bruchteil p−1 der Hintergrundsdichte
herunterzukommen, muss man bis auf einen Bruchteil
π(p − 1)
x = 2 exp −
α 0 rs
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
62
an die Fermienergie herangehen. Für rs = 3 und p = 10 ist dies 3 · 10−8 . Auch in der
Theorie ist der Effekt sehr delikat; die Einschneidung kann leicht durch Korrelationseffekte
(Abschirmung des Coulomb-Potentials) verschmiert werden. Experimentell gibt es, z.B.
in Metallen, nicht den geringsten Hinweis auf eine verschwindende Zustandsdichte an der
Fermikante.
Die mittlere Energie pro Elektron kann im Prinzip durch Summation aller kσ erhalten
werden (man braucht einen Faktor 21 weil es sich um eine Wechselwirkungsenergie handelt,
siehe S. 57, und einen Faktor 2 für die beiden Spinrichtungen). Eine direkte Rechnung ist
aber einfacher
1 4πe2 X 0
1
Eex = − 2
2 V k ,k <k |ki − kj |2
i j
F
2 Z
2
V
4πe
1
=−
dk
dk
.
1
2
V
8π 3
|k1 − k2 |2
k1 ,k2 <kF
Der Integrand kann umgeschrieben werden als
1
1
1
1
≡ 2
≡ 2
.
2
2
2
|k1 − k2 |
k1 + k2 − 2k1 k2 µ
k1 1 + s − 2sµ
Der zweite Faktor kann für s < 1 in den Legendre-Polynomen ausgedrückt werden:
"
#2
∞
X
X
1
0
L
=
s
P
(µ)
sL+L PL (µ)PL0 (µ).
=
L
2
1 + s − 2sµ
L
L,L0 =0
Das gesamte Integral setzt sich zusammen aus Beiträgen der Bereiche k2 < k1 (s < 1) und
k1 < k2 (s > 1), welche aus Symmetriegründen gleich sein müssen. Das erste Teilintegral
lässt sich mit Hilfe der obigen Formeln berechnen; für das Gesamtintegral I erhält man so
Z
I=2
Z
2πk22
dk1
k1 <kF
k2 <k1
Z
= 8π
Z
dk2
dk1
k1 <kF
0
Z
= 8π
k1 <kF
k1
dk1 k1
L+L0
∞ X
k2
1
P (µ)PL0 (µ)
dk2 dµ
2 L
k
k
1
1
0
L,L =0
2L+2
∞ X
k2
L=0
X
L
k1
1
2L + 1
∞
X
1
1
2 4
= 8π kF
.
(2L + 1)(2L + 3)
(2L
+
1)(2L
+
3)
L=0
Wegen
∞
X
∞ 1
1X
1
1
1
=
−
=
(2L + 1)(2L + 3)
2 L=0 2L + 1 2L + 3
2
L=0
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
63
erhält man letztendlich für die Austauschenergie
Eex = −
e2 V
e2 kF4 V
2 4
4π
k
=
−
.
F
16π 5
4π 3
Einsetzen der Beziehung zwischen kF und der Dichte liefert für die mittlere Austauschenergie pro Teilchen
ex = −
0,916
3e3
=−
Ry,
4πα0 r0
rs
und für die Kohäsionsenergie pro Teilchen in Hartree-Fock Näherung
2,21 0,916
koh
HF =
Ry.
−
rs2
rs
Anders als in der Hartree-Näherung erhält man also einen Ausdruck, der wenigstens für
genügend großes rs (für Metalle gilt typischerweise 2 < rs < 5) negativ werden kann
(Echte metallische Kohäsion würde übrigens erfordern, dass koh die atomare lonisationsenergie übersteigt). Nähere Diskussion des obigen Ergebnisses lohnt sich aber kaum, weil
die Hartree-Fock Näherung viel zu grob ist, um realistische Werte für die Kohäsionsenergie
zu liefern. Weiters haben wir durch Einsetzen der ebenen Wellen zwar eine Lösung der
Hartree-Fock-Gleichungen bestimmt, aber keineswegs gezeigt, dass dies auch die energetisch günstigste Lösung ist. Overhauser konnte zeigen, dass man Lösungen mit niedrigerer
Energie erhält durch das Ansetzen von Spindichtewellen; in diesen Lösungen ist die Gesamtladungsdichte konstant, aber es gibt lokal Überschüsse der einen oder anderen Spinrichtung. Dies kostet zwar kinetische Energie, aber die potentielle Energie wird abgesenkt,
weil Teilchen gleichen Spins einander aus dem Wege gehen, wie wir gleich im Detail sehen
werden. Auch die Overhauser-Lösung liefert aber noch keinen realistischen Wert für die
Kohäsionsenergie.
3.2.4
Die Korrelationsfunktion (das Austauschloch)
Zum Schluss unserer Diskussion der Hartree-Fock Näherung bestimmen wir noch die Paardichte ρ2 (r, +; r0 , +) für Elektronen gleichen Spins (die - triviale - Struktur für ungleiche
Spinrichtungen wurde schon auf S. 56 bestimmt). Aus dem Ausdruck von S. 56 für parallele
Spins folgt
i
1 Xh
0
0
1 − e−i(k−k )·(r−r )
ρ2 (r, +; r0 , +) = 2
V kk0
Z
2
2
1 N
1 −ik·(r−r0 ) =
−
dk
e
4 V
(8π 3 )2 k<kF
=
1
4
N
V
2
1 − F 2 (kF |r − r0 |) .
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
64
Das Integral in F (y) ist der Formfaktor der Einheitskugel; mit Hilfe der Beziehung
V 4π 3
1
kF = N
2
(2π) 3
2
erhält man für F (y) das Ergebnis
F (y) =
3
(sin y − y cos y).
y3
1 2
Die Funktion F (y) verhält sich für kleine y wie 1− 10
y und hat seinen ersten Nulldurchgang
π
π
π
bei y = 4 , d.h. bei r = 4 kF = 4 α0 r0 = 0,409 r0 . Das Loch in der Elektronendichte um
jedes Elektron heißt Fermi- oder Austauschloch. In einem ”reellen” Elektronengas gibt es
natürlich zusätzliche Effekte aufgrund der Coulomb-Abstoßung, die in der Hartree-Fock
Näherung nur äußerst unzureichend berücksichtigt worden sind.
3.2.5
Die Dichtefunktionalmethode
Zu einer Verbesserung des Ergebnisses der Hartree-Fock-Methode kann man durch Störungstheorie oder durch Variationsrechnung geraten. In den letzten Jahren hat sich aber
ein alternativer Zugang durchgesetzt: die Dichtefunktionalmethode. Ausgangspunkt ist ein
bemerkenswertes Theorem von Hohenberg und Kohn: Der Grundzustand der N-TeilchenSchrödingergleichung für ein System von N Elektronen in einem vorgegebenen äußeren
Potential V(r) ist im Prinzip durch die Teilchendichte ρ(1) (r) = n(r) eindeutig festgelegt.
Der Beweis erfolgt durch ”reductio ad absurdum”: Nehme an, es gäbe zwei Potentiale V1 (r)
und V2 (r), die zur selben Dichte im Grundzustand führen. Falls wir die entsprechenden
Grundzustände mit Ψ1 (r1 , . . . , rN ) und Ψ2 (r1 , . . . , rN ) bezeichnen, so gilt nach dem Ritzschen Variationsprinzip:
E10 = Ψ1 |H1 |Ψ1 < Ψ2 |H1 |Ψ2
Z
= Ψ2 |H2 |Ψ2 + dr [V2 (r) − V1 (r)] n(r),
wobei das <-Zeichen nur durch ein = ersetzt werden kann, falls V1 (r) und V2 (r) sich nur
um eine Konstante unterscheiden. Aus der obigen Ungleichung folgt
Z
E10 − E20 < dr [V2 (r) − V1 (r)] n(r).
Durch Vertauschen der Indizes 1 und 2 erhält man aber
Z
E20 − E10 < dr [V1 (r) − V2 (r)] n(r),
was einen Widerspruch ergibt. Die Annahme, zwei verschiedene V (r) führen zum selben
n(r), ist also nicht haltbar.
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
65
Es muss also ein Funktional E0 [n(r)] geben, das die Grundzustandsenergie in der zum
Grundzustand gehörenden Dichte n(r) ausdrückt. Das Funktional kann geschrieben werden
als
Z
ZZ
2
0
1
0 e n(r)n(r )
E0 [n] = T [n] + dr V (r)n(r) +
+ EXC [n],
dr dr
2
|r − r0 |
wobei T [n] die kinetische Energie und EXC [n] die Austausch- und Korrelationskorrekturen
darstellt. Sowohl T [n] als auch EXC [n] sind aber bisher noch unbekannte Funktionale. Der
Vorteil des neuen Formalismus ist aber, dass er als Ausgangspunkt für neuartige Näherungen dienen kann.
Die lokale-Dichte-Näherung
Die einfachste Näherung besteht darin, dass wir die Ergebnisse für das homogene Elektronengas nützen. Für dieses System (Jellium) gibt es recht gute Näherungen für E0J (n),
das wegen der Homogenität kein ”echtes” Funktional, sondern lediglich eine Funktion von
J
n ist, und deshalb auch für EXC
(n). Wir ersetzen nun das exakte Funktional EXC [n] durch
Z
J
EXC [n] ' dr EXC
(n(r)) ,
also durch einen gewichteten Mittelwert der Werte für homogenes Jellium.
Die nächste Beobachtung ist, dass das Funktional
E0 [n] einem Variationsprinzip ähnlich
dem Rayleigh-Ritz-Prinzip gehorcht (weil Ψ|H1 |Ψ sein Minimum für Ψ1 annimmt und
Ψ1 durch n(r) bestimmt ist). Die Variation von E0 [n] nach n lautet in der lokalen-DichteNäherung:
δT
δE0
=
+ V (r) + Φdir (r) + µXC (r) = 0,
δn
δn
wobei
Z
Φdir (r) =
dr0
e2 n(r0 )
;
|r − r0 |
µXC (r) =
J
dEXC
(n(r))
.
dn
Dieses Variationsprinzip ist identisch zu demjenigen für ein Gas aus nichtwechselwirkenden
Teilchen im effektiven Potential
Vef f (r) = V (r) + Φdir (r) + µXC (r).
Für dieses äquivalente System ist der Grundzustand gegeben als eine Slaterdeterminante
aus den N niedrigsten Eigenfunktionen der sog. Kohn-Sham-Gleichung:
~2 2
∇ + Vef f Φ(r) = KS Φ(r);
(2.3)
−
2m
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
66
diese Gleichung ist, wie die Hartree-Gleichung, bei vorgegebenem n(r) numerisch lösbar.
Wie bei der Hartree-Gleichung kann man also iterativ vorgehen: Zuerst löst man (2.3) für
eine Versuchsfunktion n0 (r); aus den N niedrigsten Eigenfunktionen konstruiert man dann
über die Slater-Determinante ein n1 (r), bestimmt daraus ein neues Vef f (r) und wiederholt
das Verfahren, bis man in genügender Näherung Konsistenz erreicht hat.
Die Dichtefunktionalmethode in der lokalen-Dichte-Näherung hat zu einem Durchbruch
bei der Berechnung der Struktur von Atomen, Molekülen und Festkörpern geführt. Gegenüber einer direkten Lösung der Schrödingergleichung hat sie aber den Nachteil, dass sie
nicht systematisch ist (Variationsrechnung: untere Grenze; Störungsrechnung: fester Algorithmus). Seit den ersten Arbeiten von Kohn et a. hat es weitere Entwicklungen gegeben;
insbesondere sind Korrekturen zur lokalen-Dichte-Näherung vorgeschlagen worden, in denen auch Ortsabhängigkeiten über die Ableitungen von n(r) mitgenommen werden. Auch
diese Varianten bilden aber noch keine voll systematische Theorie.
Literatur
∗ Einführend:
→ Physics Today, December 1998, p 21
∗ Originalarbeiten:
→ P. Hohenberg, W. Kohn, Phys. Rev. B 136, 864 (1964)
→ W. Kohn, L.J. Sham, Phys. Rev. A 140, 1133 (1965)
3.3
Die Elektron-Phononwechselwirkung; Polaronen
In diesem Abschnitt werden wir die Elektron-Phonon-Wechselwirkung in einem Festkörper
diskutieren. Unser wichtigstes Ziel dabei ist es, die Diskussion der BCS-Theorie der Supraleitung vorzubereiten. Weil in der BCS-Theorie nur die niedrigfrequenten Phononen eine
Rolle spielen, und deren Verhalten von Einzelheiten der Gitterstruktur weitgehend unabhängig ist, werden wir uns in der Diskussion der Phononen auf einfache hochsymmetrische
Kristalle beschränken, sofern die Diskussion und die Formeln dadurch einfacher werden.
3.3.1
Gitterschwingungen und ihre Quantisierung; Phononen
Im vorhergehenden Kapitel wurde skizziert, wie man im Prinzip die elektronische Grundzustandsenergie für ein System von Elektronen in einem vorgegebenen äußeren Potential
berechnet, insbesondere im Potential einer vorgegebenen Anordnung von lonenrümpfen.
Für eine vorgegebene Zahl von Ionenrümpfen (oder sogar von Kernen) in einem vorgegebenem Volumen wird diese Grundzustandsenergie von der Anordnung der Rümpfe abhängen,
und i.a. ihr Minimum für irgendeine periodische Anordnung erreichen, wobei jedes Ion auf
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
67
einem Gitterplatz Rnα sitzt, mit
Rnα = Rn + cα = n1 a1 + n2 a2 + n3 a3 + cα ;
dabei sind die ai drei Gittervektoren; die ni sind ganze Zahlen mit 0 ≤ ni ≤ Ni ; N1 N2 N3 =
N/s, und die Zahl s bezeichnet die Zahl der Plätze, charakterisiert durch die Vektoren cα
mit 1 ≤ α ≤ s, innerhalb einer Gitterzelle. Gitterplätze verschiedener cα können mit Ionen
verschiedener Art besetzt sein. Wir betrachten im weiteren Konfigurationen des Gitters,
in denen jedes Ion sich nahe ”seinem” Gitterpunkt befindet:
rnα = Rnα + snα ,
und betrachten die potentielle Energie nur bis zu quadratischen Termen in den snα :
1 X
E ({snα }) = E0 +
Φnαi
0 0 snαi sn0 α0 j
2 nn0 αα0 ij n α j
mit E0 = E({0}); die Entwicklungskoeffizienten Φnαi
n0 α0 j heißen Kraftkonstanten. Zwischen
den Kraftkonstanten existieren viele strukturabhängige Symmetriebedingungen. Die
wichtigsten sind:
a) Symmetrie
0 0
nαj
Φnαi
n0 α0 j = Φnαi
b) Invarianz gegenüber Gittertranslationen:
(n−n0 )αi
Φnαi
n0 α0 j = Φoα0 j
(d.h. der Energieaufwand für eine Auslenkung zweier Ionen hängt nur vom Abstand
der Gleichgewichtspositionen, nicht aber von deren absoluten Orten ab.)
c) Invarianz gegenüber starren Verschiebungen des Gitters
X n0 α0 j
Φnαi = 0.
nα
Die Hamiltonfunktion für die Gitterschwingungen kann jetzt geschrieben werden als
HG =
1X
1 X
mα (ṡnα )2 +
Φnαi
0 0 snαi sn0 α0 j .
2 nα
2 nn0 αα0 ij n α j
(3.1)
Dies ist die aus der Vorlesung Mechanik bekannte Form für kleine Schwingungen um ein
Gleichgewicht. Es existieren zeitlich periodische Normalschwingungen vom Typ
s(p)
nα (t) = √
1
u(p) e−iωp t
mα nα
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
68
−1/2
(p)
mit zeitunabhängigen unα . (Der Faktor mα
bewirkt, dass die u(p) zu verschiedenen ωp
(p)
orthogonal zueinander stehen; für die s gilt mit mα gewichtete Orthogonalität; siehe
Skriptum Mechanik). Die Eigenwerte ωp folgen aus der Eigenwertgleichung
0 0
(p)
ωp2 unαi
=
X
n0 α0 j (p)
Dnαi
un0 α0 j
mit
n0 α0 j
Dnαi
n0 α0 j
Φn α j
≡ √ nαi .
mα mα0
Wegen der Invarianz bezüglich Gittertranslationen lässt sich dieses (3N ×3N )-Eigenwertproblem
in N/s unabhängige (3s × 3s)-Eigenwertprobleme zerlegen mit dem Ansatz
r
s qβ iq·Rn
(p)
qβ
c e
.
1 ≤ β ≤ 3s
(3.2)
unαi ≡ unαi =
N αi
Hierdurch reduziert sich die obige Eigenwertgleichung zu
"
#
X
X
0 −n)α0 j
(n
2 qβ
ωqβ
cαi =
Doαi
eiq·(Rn −Rn0 ) cqβ
α0 j
α0 j
≡
X
(3.3)
n0
α0 j
Dαi
(q)cqβ
α0 j .
α0 j
Die N/s Gittervektoren q haben die Gestalt
qm =
m1
m2
m3
b1 +
b2 +
b3 ;
N1
N2
N3
0 < mi < Ni ,
(3.4)
wobei bi die Basisvektoren des reziproken Gitters sind, charakterisiert durch
bi ·aj = 2πδij .
Die Lösungen (3.2) mit den q-Vektoren (3.4) erfüllen periodische Randbedingungen für ein
Volumen bestehend aus N1 × N2 × N3 Einheitszellen. Die Einschränkung in (3.4) zur sogen.
ersten Brillouin-Zone verhindert Doppelzählungen: Man überzeugt sich leicht, dass die
Substitution
q m → q m + Gp
mit Gp = p1 b1 + p2 b2 + p3 b3
mit ganzzahligen pi die Eigenvektoren uqβ
nαi unverändert lässt.
Normalkoordinaten
Wenn wir die Lösungen des Eigenwertproblems (3.3) gemäß
X
αi
∗
0
qβ qβ
cαi
cαi = δββ 0
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
69
normieren, können wir die allgemeinste Lösung der aus (3.1) hergeleiteten Bewegungsgleichungen in der Form
r
X
s qβ iq·Rn
cαi e
snαi (t) =
Qqβ (t)
N
m
α
qβ
schreiben. Falls wir weiters die cqβ
αi so wählen, dass gilt
∗
,
c−qβ
=
cqβ
αi
αi
was aufgrund der Form der Eigenwertgleichung (3.3) erlaubt ist, und weiters die Identität
X
n
0
ei(q−q )·Rn =
N
∆(q − q0 )
s
benützen, wobei ∆(q) gleich eins ist für den Nullvektor oder jeden anderen Vektor des
reziproken Gitters, und null für alle sonstigen Vektoren, so lässt sich die Hamiltonfunktion
HG mittels einer etwas mühsamen Rechnung in
1X
1 X
2
2
HG =
Q̇qβ Q̇−qβ + ωqβ
Qqβ Q−qβ =
Pqβ P−qβ + ωqβ
Qqβ Q−qβ ,
2 qβ
2 qβ
umformen, wobei die Pqβ und Qq0 β 0 die üblichen Poisson-Klammern für Koordinaten und
Impulse erfüllen.
Die Quantisierung der Gitterschwingungen geschieht mittels der Substitution
s
~ †
aqβ + a−qβ ;
Qqβ =
2ωqβ
r
~ωqβ Pqβ = −i
a−qβ − a†qβ ,
2
wobei die aqβ und a†qβ Erzeuger und Vernichter für Bosonen sind. Die so erhaltenen
Boseteilchen heißen Phononen. Die Hamiltonfunktion in diesen Variablen erhält die schon
vertraute Form
X
1
†
~ωqβ aqβ aqβ +
,
H=
2
qβ
und wir können auch für die Phononen eine Besetzungszahldarstellung einführen. Die Nullpunktsenergie des Phononensystems liefert einen Beitrag zur Grundzustandsenergie und
muss als solche neben der elektronischen Grundzustandsenergie beim Vergleich zweier ”konkurrierender” Kristallstrukturen berücksichtigt werden. Dynamisch spielt sie aber keine
Rolle.
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
70
Optische und akustische Phononen
2
Aus der Struktur des Eigenwertproblems geht hervor, dass die ωqβ
analytische Funktionen
qβ
von q sind, und dass die cαi analytisch gewählt werden können. Andererseits weiß man,
dass es für q = 0 drei Eigenvektoren zu ω = 0 gibt, nämlich die starren Verschiebungen des
Gitters. Es müssen sich also unter den 3s Funktionen ωqβ = ωβ (q) mindestens 3 befinden,
die für q ↓ 0 nach Null gehen. Andererseits lässt sich zeigen, dass die Anwesenheit von mehr
als 3 nach Null strebenden Frequenzen, sowie von ωβ (q), die langsamer als q ansteigen, mit
der Stabilität der Kristallstruktur unvereinbar ist. Für Kristalle genügend hoher Symmetrie
(z.B. kubische Kristalle) gibt es drei sog. akustische Zweige, einen longitudinalen mit
cqβ
α k q;
ωβ (q) = cl q + O(q 2 )
und zwei entartete transversale mit
ωβ (q) = ct q + O(q 2 ),
cqβ
α ⊥ q;
wobei cl und ct die longitudinale, bzw transversale Schallgeschwindigkeit bezeichnen. Wenn
wir uns vom Punkt q = 0 entfernen, so geht die strenge Trennung zwischen longitudinalen
und transversalen Schwingungen, sowie die Entartung der zwei vorwiegend transversalen
Zweige, außer in einigen hochsymmetrischen Richtungen im Kristall, allmählich verloren.
Die 3(s − 1) weiteren Phononenzweige werden optische Zweige genannt.
3.3.2
Die Elektron-Phonon-Wechselwirkung
Wir betrachten jetzt einen Kristall mit Ein-Elektron-Orbitalen vom Bloch-Typ
1
Φkνσ (x) = √ eikr ukν (r)χσ (sz ),
V
mit einer gitterperiodischen Funktion ukν (r), und untersuchen den Einfluss einer Auslenkung des Ions n, α. Diese Auslenkung hat einen direkten Einfluss auf das Potential der
Ionen das auf die Elektronen am Ort r wirkt; in niedrigster Ordnung gilt
V (r) =
X
nα
vα (r − rnα ) =
= V0 (r) −
XX
nαi qβ
X
nα
r
Qqβ
[vα (r − Rnα ) − snα ∇vα (r − Rnα )]
s qβ iqRn ∂
c e
vα (r − Rnα ),
N mα αi
∂ri
wobei V0 (r) das äußere Potential des ungestörten Gitters darstellt. Im Hamiltonoperator
für das Fermionfeld erhält man so einen zusätzlichen Term
Z
Hel-ph = dx ψ † (x) [V (r) − V0 (r)] ψ(x).
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
71
Substitution der Modenentwicklungen für ψ und ψ † liefert
X
qβ
Hel-ph = −
aqβ + a†−qβ c†k0 ν 0 σ ckνσ
Mkνk
0ν0
kνk0 ν 0 σ
qβ
mit
qβ
Mkνk
0ν0 =
XZ
s
~s
iqRn i(k−k0 )r
∗
e
.
cqβ
αi uk0 ν 0 (r)ukν (r)∇i vα (r − Rnα ) × e
2
2N mα ωqβ V
dr
nαi
Als nächstes setzen wir für vα (r − Rnα ) eine Fourierreihe ein. Dies liefert
X
0
0
∇i vα (r − Rnα ) = i
e−iq Rn qi0 vαq0 eiq r ,
q0
wobei wir einen Faktor exp(−iq0 cα ) in vαq0 absorbiert haben. Ausführen der Summation
über n liefert einen Faktor
NX
N
4(q − q0 ) =
δq0 , q+Gp ;
s
s p
das r-Integral enthält also außer gitterperiodischen Faktoren nur noch den Exponentialfaktor
exp [i(k + q + Gp − k0 )r] ,
und es verschwindet, wenn nicht k0 = k + q + Gp + Gp0 . Für genügend glatte ukν (r) ist
nur der Term mit Gp0 = 0 wichtig, und wir erhalten nach sämtlichen Substitutionen
s
Z
X
~N
qβ
(q + Gp )cα
dr u∗(k+q+Gp )ν 0 (r)ukν (r)
Hel-ph = − i
2sm
ω
α
qβ
τ
kνν 0
αGp qβ
vα(q+Gp ) aqβ + a†−qβ c†(k+q+Gq )ν 0 σ ckνσ ,
wobei das r-Integral über eine Gitterzelle läuft. Der Wechselwirkungsterm beschreibt Prozesse, in denen ein Elektron vom Zustand kνσ in den Zustand (k + q + Gp )ν 0 σ übergeht
und dabei ein Phonon mit Quasiimpuls q absorbiert oder ein Phonon mit Quasiimpuls
−q emittiert. Ein Übergang ist natürlich nur möglich, wenn der Ausgangszustand besetzt
und der Endzustand leer ist. Weil typische Phononenergien klein sind gegenüber der Breite
typischer Bänder, spielen für Metalle nicht zu weit vom Gleichgewicht nur Übergänge innerhalb des Bandes, in dem das Fermi-Niveau liegt eine Rolle; wir werden einfachheitshalber
annehmen, dass dieses Band nicht entartet ist, und dass die Fermioberfläche nicht zu nahe
an die Ränder der Brillouin-Zone kommt, so dass man auch die Umklappprozesse mit
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
72
Gp 6= 0 vernachlässigen kann. Dies hat wieder zur Folge, dass nur longitudinal polarisierte Phononen für die Wechselwirkung eine Rolle spielen. Für Elementkristalle entfällt
auch noch die Summation über α und nur der longitudinale akustische Phononzweig trägt
bei. Nach allen diesen Vereinfachungen erhält man
s
Z
X
~N
†
ql
∗
qc vq dr uk+q (r)uk (r) aq + a−q c†k+q,σ ckσ
Hel-ph = −i
2mωql
τ
kqσ
X
≡
Mkq aq + a†−q c†k+q,σ ckσ ,
(3.5)
kqσ
wobei wir den Index l bei den Phononen-Erzeugern und -Vernichtern weggelassen haben.
Für breite Bänder ist auch die k-Abhängigkeit von Mkq , die auf die uk (r) zurückzuführen
ist, sehr viel weniger ausgeprägt als die q-Abhängigkeit.
Die Wechselwirkung (3.5) beschreibt den Einfluss der Phononen auf die Elektronenniveaus noch nicht vollständig; eine Änderung der Positionen der Ionen bringt eine Umverteilung der Dichte der Elektronen, und damit eine Änderung des selbstkonsistenten
Elektron-Elektronpotentials mit sich. Effekte dieser Art führen aber zu Termen derselben
Ordnung wie die in (3.5) enthaltenen (bis zur niedrigsten Ordnung in den Phononkoordinaten); lediglich die Interpretation der Mkq ändert sich.
Abbremsung von Elektronen durch Phononenemission
Unter Einfluss der Elektron-Phonon-Wechselwirkung kann ein Elektron mit Wellenvektor
k in ein Elektron mit Wellenvektor k − q und ein longitudinales Phonon mit Wellenvektor
q zerfallen. Dabei muss aber Energieerhaltung gelten:
k − k−q − ~ωq = 0,
was für parabolische Bänder und unter Vernachlässigung der Phonondispersion zu
~
2kq − q 2 = cl q
2m∗
führt. Der Mindestwert von k, für den diese Gleichung erfüllt sein kann, ist
1
~kmin = ~q + m∗ cl ,
2
oder, weil q beliebig klein gewählt werden kann,
~kmin = m∗ cl .
Dies bedeutet, dass nur Elektronen, deren Gruppengeschwindigkeit vg = ~k/m∗ die longitudinale Schallgeschwindigkeit übertrifft, durch Emission von Phononen zerfallen (akustische Cerenkov-Strahlung).
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
73
Virtuelle Phononen, das Polaron
In unserer Diskussion der Lamb-Verschiebung haben wir gesehen, dass die Wechselwirkung
eines Atoms mit dem
zur Folge hat, dass das Atom dauernd zwischen den
Strahlungsfeld
Zuständen |A; {0} und |B; 1k hin und her pendelt. Auf ähnliche Weise befindet sich ein
Elektron mit Wellenvektor k aufgrund
der Elektron-Phonon-Wechselwirkung
für einen Teil
der Zeit in Zuständen |1k−q,σ ; 1q , |1k−q−q0 ,σ ; 1q 1q0 usw., wobei die angegebenen Zustände
nicht energetisch mit |1kσ ; {0} entartet zu sein brauchen. Die Phononen können also
nicht frei durch den Kristall laufen; sie müssen in der Nähe des Elektrons bleiben, um
wieder reabsorbiert zu werden, ”ehe die Verletzung der Energieerhaltung bemerkt werden
kann". Das Elektron schleppt also eine Wolke virtueller Phononen mit sich. Die kombinierte
Anregung heißt Polaron. Für schwache Elektron-Phonon-Wechselwirkung lässt sich der
Aufbau des Polarons mittels Störungsrechnung
bestimmen. In niedrigster Ordnung gilt für
den Ein Polaron-Zustand |1kσ ; {0} p der Ausdruck
|1kσ ; {0}
p
X
= |1kσ ; {0} +
q
Mkq
|1k−q,σ ; 1q .
k − k−q − ~ωql
Genau wie bei der Lamb-Verschiebung führt die Beimischung von Zuständen mit virtuellen
Phononen auch zu einer Verschiebung der Energieniveaus (allerdings hat man wegen der
endlichen Zahl der Phononanregungen keinerlei Divergenzschwierigkeiten). Wir werden die
Berechnung der Energieverschiebungen aber nicht weiter verfolgen.
Elektron-Elektron-Wechselwirkung durch Phononaustausch
In untenstehender Skizze wird ein Prozess veranschaulicht, der in zweiter Ordnung in Hel−ph
auftritt und der zu einer effektiven Wechselwirkung zwischen den Elektronen führt. Das
besondere daran ist, dass diese Wechselwirkung unter Umständen attraktiv sein kann;
dies ist für die Erklärung der Supraleitung wesentlich.
k+q
k' - q
k' - q
k+q
q
k'
k
k'
-q
k
(Nebenbei sei bemerkt, dass in der relativistischen Quantenelektrodynamik die Coulombwechselwirkung zwischen geladenen Teilchen auf völlig analoge Weise als eine Folge des Austausches eines Photons zwischen den Teilchen gedeutet wird.) Die Amplitude
für den skizzierten Prozess erhält man genauso wie die Amplitude für die Streuung von
Photonen an einem Atom (Kapitel 2.3.5, S. 29). Wenn wir die k-Abhängigkeit von Mkq
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
74
vernachlässigen und die Beziehung
M−q = Mq∗
ausnützen, welche aus der Definition von Mkq und der Konvention auf S. 68 über die
Polarisationsvektoren cqβ
α folgt, so erhalten wir
1
1
2
+
c(t) ∼ |Mq |
.
k0 − k0 −q − ~ωq k − k+q − ~ωq
Die hieraus folgende Übergangswahrscheinlichkeit enthält einen Faktor t δ (k0 −q + k+q − k0 − k );
wenn man nur in der Übergangsrate in niedrigster Ordnung interessiert ist, kann man durch
Substitution der δ-Funktion den Ausdruck in eckigen Klammern noch etwas umformen:
1
1
[. . . ] = −
+
~ωq + (k − k+q ) ~ωq − (k − k+q )
+2~ωq
=
.
(k − k+q )2 − ~2 ωq2
Dieselbe Übergangsamplitude würde man aus einer effektiven Wechselwirkung
eff
Hel-el
1 X
+2 |Mq |2 ~ωq
c†k0 −q,σ0 c†k+q,σ ckσ ck0 σ0
=
2
2
2
2 kk0 qσσ0 (k+q − k ) − ~ ωq
erhalten. (Die Reihenfolge der Fermionoperatoren ist äquivalent mit den in dem Störungsausdruck zweiter Ordnung in den Amplituden auftretenden Reihenfolgen c†k+q,σ ckσ c†k0 −q,σ0 ck0 σ0
bzw c†k0 −q,σ0 ck0 σ0 c†k+q,σ ckσ ; der Faktor 21 tritt auf, weil der Übergang von q nach −q dasselbe
bewirkt wie die Vertauschung der zwei Diagramme in der Skizze auf S. 73).
Die obige Herleitung der effektiven Wechselwirkung kann auch etwas vornehmer durchgeführt werden, indem man die Erzeuger und Vernichter für die Elektronen zugunsten
derjenigen für die Polaronen eliminiert. Dies kann mit Hilfe einer kanonischen Transformation geschehen, siehe Madelung, Festkörpertheorie II, §81; das Ergebnis ist aber dasselbe.
Ein Vergleich mit der Fourierdarstellung des Ausdrucks (1.3) auf S. 52 ergibt, dass die
oben hergeleitete Wechselwirkung repulsiv ist für |k+q − k | > ~ωq und attrativ für
|k+q − k | < ~ωq .
3.4
Die BCS-Theorie der Supraleitung
In diesem Abschnitt werden wir zeigen, dass die Elektron-Phonon-Wechselwirkung dazu
führen kann, dass der Grundzustand des Elektronensystems sich radikal ändert. Wir werden
dabei vom Hamiltonoperator
X †
1 X
Vkk0 q c†k0 −q,σ0 c†k+q,σ ckσ ck0 σ0
H=
k ckσ ckσ +
2 kk0 σσ0 q
kσ
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
75
ausgehen. Dabei haben wir vernachlässigt, dass die k nicht wirklich Ein-Teilchen-Energien
sind. Dieser Fehler ist nicht sehr bedeutsam, solange wir nur Zustände betrachten, in denen
nur eine kleine Zahl von Elektronen angeregt sind.
Cooper-Paare
Cooper betrachtete für den obigen Hamiltonoperator den Fall, dass alle Niveaus bis zum
Fermi-Niveau besetzt sind, und dass zwei zusätzliche Elektronen in das System hineingebracht werden. Er suchte jetzt den niedrigsten Zustand für diese Zusatzelektronen; falls die
Wechselwirkung zwischen den Elektronen vorwiegend attraktiv ist, kann man gebundene
Zustände erwarten; insbesondere erwartet man den niedrigsten Wert für die Energie für
einen verschwindenden Gesamtimpuls des Paares, und für antiparallele Spins (für die das
Pauliverbot die Elektronen nicht daran hindert, das attraktive Potential auszunützen). Wir
wählen also für den Zwei-Teilchen-Zustand den Ansatz
X
|ψ =
α(k)c†k↑ c†−k↓ |0HF .
|k|>kF
Für die Energie dieses Zustandes erhält man
E − E0,HF = 2
X
k>kF
k |α(k)|2 +
1X
(Vk,−k,q + V−k,k,−q ) α∗ (k + q)α(k).
2 k,q
Dieser Ausdruck muss unter der Nebenbedingung
führt zu den Euler-Lagrange-Gleichungen
2k α(k) +
P
k
|α(k)|2 = 1 minimiert werden. Dies
1X
(Vk−q,−k+q,q + V−k+q,k−q,−q ) α(k − q) − λα(k) = 0.
2 q
(4.1)
(Bei der Ableitung des Potentialterms nach α∗ (k) muss eine Variablentransformation
k ⇒ k − q durchgeführt werden.) Durch Multiplikation der oberen Gleichung mit α∗ (k)
und Summation über k erhält man für λ die Interpretation
λ = E − E0,HF .
Um einen Eindruck der möglichen Lösungen von (4.1) zu erhalten, führen wir eine zuerst
von Bardeen vorgeschlagene vereinfachte Form für die Wechselwirkung V ein. Wir wissen
schon, dass der von Phononen vermittelte Teil von V attraktiv ist für |k+q − k | < ~ωq .
Bardeen schlug als Näherung vor
(
−W für |k − F | und |k+q − F | < ~ω0 ;
Vk,−k,q =
0
für sonstige Werte von k und q.
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
76
Dabei ist ω0 eine typische Frequenz von der Größe der Debye-Frequenz. Mit dieser vereinfachten Wechselwirkung erhält man für die obige Gleichung
X
(2k − λ)α(k) = W
α(k0 )
für F < k < F + ~ω0 ;
F <k0 <F +~ω0
sonst.
α(k) = 0
Diese Gleichung ist exakt lösbar, weil die Summe nicht mehr von k abhängt und durch
eine Konstante A ersetzt werden kann. Die Lösung ist
α(k) =
AW
2k − λ
für F < k < F + ~ω0 ,
und der Eigenwert λ folgt aus der Konsistenzbedingung
A=
X
X
α(k) =
F <k <F +~ω0
k
AW
.
2k − λ
Weil ~ω0 F können wir bei der Umformung der Summe über k in ein Integral über
die Zustandsdichte im gesamten Integrationsintervall gleich der Zustandsdichte an der
Fermienergie g(F ) setzen, und erhalten
Z
~ω0
d
1 = g(F )
0
W
2 − (λ − 2F )
mit der Lösung
1
W g(F ) ln
2
2~ω0 − (λ − 2F )
−(λ − 2F )
= 1,
was für kleine Werte von W g(F ) geschrieben werden kann als
−(λ − 2F ) = 2~ω0 e−2/W g(F ) .
Wir haben also wirklich einen gebundenen Zustand der zwei Zusatzelektronen gefunden.
Dies bedeutet aber zugleich eine Instabilität des Hartree-Fock-Grundzustands:
auch für die schon anwesenden Elektronen in den oberen Niveaus ist es energetisch vorteilhaft, sich aus den Ebenen-Wellen-Zuständen zu entfernen und Cooper-Paare zu bilden. Diese können dann aber bei genügend hoher Dichte der Paare nicht länger als unabhängig betrachtet werden, und wir brauchen einen neuen Ansatz für die GrundzustandsWellenfunktion. Der neue Ansatz kann nicht mit Störungstheorie erhalten werden. Der
Ausdruck für die Bindungsenergie eines Cooper-Paares enthält W −1 im Exponenten; er
ist also nichtanalytisch in der Kopplungskonstanten W . Störungstheorie dagegen liefert
immer Ausdrücke, die analytische Funktionen der Kopplungskonstante sind.
77
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
Ehe wir dieses Problem näher betrachten, werden wir noch zeigen, dass die BardeenWechselwirkung keine Triplett-Paare vom Typ
X
|ψ t =
β(k)c†k↑ c†−k↑ |0HF
|k|>kF
zulässt. Wegen
c†k↑ c†−k↑ |0HF = −c†−k↑ c†k↑ |0HF
trägt nur der in k antisymmetrische Teil von β(k) zum Zustand |ψ
β(−k) = −β(k) setzen. Dann verschwindet aber die Größe
X
B≡
β(k),
t
bei und wir können
k
und die Integralgleichung für λ − 2F hat nur die triviale Lösung λ = 2F mit β(k) = 0.
Für allgemeinere Formen der Wechselwirkung sind aber Triplett-Paare durchaus möglich;
für den suprafluiden Grundzustand von 3 He treten sie in gewissen Parameterbereichen
auf und auch für Supraleiter gibt es diesbezügliche Spekulationen. Triplett-Paare würden
insbesondere die Koexistenz von Supraleitung und Ferromagnetismus ermöglichen,
wofür es allerdings im Experiment keinerlei Hinweise gibt.
Der BCS-Grundzustand
Wir versuchen jetzt einen alternativen Grundzustand zu konstruieren, in dem die attraktive
Wechselwirkung so gut wie möglich ausgenützt wird. In einem System aus vielen Fermionen
tritt dabei eine Komplikation auf: sogar für positives W haben die Matrixelemente der
Wechselwirkung zwischen den Komponenten eines Zustandes
X
|ψ t =
γ ({nkσ }) |{nkσ }
(4.2)
{nkσ }
scheinbar regellos verteilte Vorzeichen aufgrund der auf S.49 eingeführten Jordan-WignerPhasen. Die von Bardeen, Cooper und Schrieffer vorgeschlagene Lösung für dieses
Problem ist:
1 Nummeriere die Zustände so, dass die Orbitale für k und −k immer in der Reihenfolge
k ↑; −k ↓; −k ↑; k ↓ vorkommen.
2 Lasse in der Superposition (4.2) nur solche {nkσ } zu, in denen die Orbitale k ↑ und
−k ↓ entweder beide besetzt oder beide leer sind; wähle weiters alle γ ({nkσ }) reell und
positiv. (Eine andere Nummerierung der Orbitale führt zu einer sehr komplizierten Wahl
für die Vorzeichen der γ ({nkσ }).)
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
78
Hierdurch hat man erreicht, dass wenigstens alle Beiträge zum Erwartungswert des
reduzierten Wechselwirkungsoperators
I
Hred
= −W
0
X
c†k↑ c†−k↓ c−k0 ↓ ck0 ↑
k,k0
positiv sind. (Der Faktor 21 ist verschwunden, weil wir alle Terme so umgeordnet haben,
dass der erste Erzeuger mit dem Spin ↑ vorkommt.) Der Strich beschränkt die Summation
auf ein Band der Breite 2~ω0 um F .
Der zweite von BCS angewandte Trick ist, dass sie sich im Zustand (4.2) nicht
P beschränken auf Komponenten mit einer vorgegebenen Gesamtteilchenzahl N = kσ nkσ .
Diese Erweiterung des Raumes der erlaubten Zustände wird es, wie in der großkanonischen
Gesamtheit der statistischen Physik, erlauben, die Besetzungswahrscheinlichkeiten für die
Paare (k ↑, −k ↓) unabhängig voneinander zu wählen. Weiters führt es zu nichtverschwindenden Erwartungswerten der Erzeuger und Vernichter für Paare
ψ|c−k↓ ck↑ |ψ = ψ|c†k↓ c†−k↑ |ψ = D(k).
Die obigen Überlegungen dienten lediglich als Motivation für die nachfolgende formale
Vorgangsweise:
I Führe einen reduzierten Hamiltonoperator ein für die Orbitale F − ~ω0 < k <
F + ~ω0 . (Die niedrigeren Orbitale sind alle besetzt; die höheren alle leer.) Wir verwenden weiters die Konvention, dass der Index k für k ↑ steht und der Index −k
für −k ↓. Schließlich nehmen wir nur den oben angegebenen reduzierten Wechselwirkungsoperator mit:
0
0
X
X
†
†
Hred =
k ck ck + c−k c−k − W
c†k c†−k c−k0 ck0 .
k,k0
k
Wir rechnen weiters die k immer relativ zum Ferminiveau. Aus diesem Hamiltonoperator folgen die Bewegungsgleichungen
i~ċk = k ck −
i~ċ†−k
=
W c†−k
−k c†−k
0
X
c−k0 ck0
k0
− W ck
X
c†k0 c†−k0
k0
II Ersetze in diesen Bewegungsgleichungen die Summen durch ihre Erwartungswerte im
gesuchten Grundzustand
0
X
k
0
X
k
0
0
X
X
c−k ck →
c−k ck ≡
D(k) ≡ 4/W
c†k c†−k →
k
0
X
k
† † ck c−k ≡
k
0
X
k
D∗ (k) ≡ 4∗ /W.
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
79
Mit Hilfe dieser Variante des Hartree-Fock-Ansatzes erhält man aus dem obigen System
die linearen, bezüglich k entkoppelten, Gleichungen (wir wählen 4 weiters reell)
i~ċk = k ck − 4c†−k ;
i~ċ†−k = −k c†−k − 4ck .
Diese Gleichungen haben Operator-Lösungen vom Typ
1
1
αk = uk ck − vk c†−k ≡ cos θk ck − sin θk c†−k
2
2
1
1
†
α−k
= uk c†−k + vk ck ≡ cos θk c†−k + sin θk ck ,
2
2
die von der Zeit abhängen gemäß
αk (t) = αk (0)e−iλk t/~
(4.3)
†
†
(0)e+iλk t/~ ,
(t) = α−k
α−k
wobei λk aus der Eigenwertgleichung
λk − k
4
= λ2k − 2k − 42 = 0
4
λk + k folgt; die positive Wurzel ist also
q
λk = 2k + 42 .
Die in (4.3) gewählte Normierung bewirkt, dass die αk und αk† die für Fermion-Erzeuger
und -Vernichter charakteristischen Antikommutatoren besitzen:
n
o
1
1
†
2
2
2
2
αk , αk = uk + vk = sin
θk + cos
θk = 1;
2
2
{αk , α−k } = uk vk − vk uk = 0,
usw. Die uk und vk bestimmt man durch Substitution in die Eigenwertgleichung:
oder:
bzw.:
λk uk = k uk + 4vk
λ2k u2k = 2k + 42 u2k = 2k u2k + 42 vk2 + 2k 4uk vk
42 u2k − vk2 = 2k 4uk vk .
Einsetzen der trigonometrischen Darstellung liefert
4
4 cos θk = k sin θk
⇒ tan θk = ,
k
oder auch
"
#
1
1
k
1
k
2
uk = (1 + cos θk ) =
1+ p 2
=
1+
2
2
2
λk
k + 42
1
1
k
vk2 = (1 − cos θk ) =
1−
,
2
2
λk
(4.4)
woraus klar hervorgeht, dass beim Übergang k → −k auch die uk und vk ihren Wert
austauschen; die physikalische Bedeutung dieses Faktums wird gleich erläutert werden.
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
80
Die explizite Form des Grundzustandes
Weil die αk die Energie eines Zustandes um λk erniedrigen, muss der Grundzustand des
Systems von allen αk vernichtet werden. Diese Bedingung wird erfüllt vom Zustand
|ψBCS
∼
=
0
Y
k
α−k αk |{0} ,
wie aus der Antivertauschung der {αk } und aus αk0 αk0 = 0 hervorgeht. Mit Hilfe der
Ausdrücke (4.3) lässt sich dies umschreiben zu
" 0
#
Y
(−vk ) uk + vk c†k c†−k |{0} ,
k
wobei Terme mit einem auf |{0} wirkenden Vernichter weggelassen wurden. Der korrekt
normierte Zustand ist
" 0
#
Y
† †
|ψBCS =
uk + vk ck c−k |{0} ,
k
wie aus
0
Y
ψBCS |ψBCS =
u2k + vk2 = 1
k
sofort hervorgeht. Der Zustand |ψBCS kann auch aufgefasst werden als ein kohärenter
Zustand für Cooperpaare mit dem Paarerzeuger
†
A ∼
0
X
k
1
tan θk c†k c†−k ,
2
(weil kein Paar mehrfach besetzt werden kann, bleiben von exp αA† |{0} genau die in
|ψBCS auftretenden Terme übrig; wir werden die korrekte Normierung von A† hier nicht
explizit bestimmen).
Ehe wir unsere Rechnung weiter verfolgen, und insbesondere den noch immer nicht
festgelegten Parameter 4 selbstkonsistent bestimmen, müssen
wir noch eine weitere Konsistenzbedingung kontrollieren: Damit der Zustand |ψBCS mit |0HF verglichen werden
kann, muss er zumindest im Mittel die gleiche Teilchenzahl N/2 aufweisen. Um den
P
Erwartungswert von 0k c†k ck + c†−k c−k zu bestimmen, müssen die ck und c†k zuerst in
den αk und αk† ausgedrückt werden. Aus den Beziehungen (4.3) schließt man sofort
†
ck = uk αk + vk α−k
;
c−k = uk α−k − vk αk† ,
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
81
woraus folgt
†
|ψBCS = vk2 .
ψBCS |c†k ck |ψBCS = vk2 ψBCS |α−k α−k
Weil die vk2 für k-Werte mit entgegengesetzten k sich zu eins summieren, erhält man in der
Tat im Mittel den Wert 21 für den obigen Erwartungswert, vorausgesetzt, dass die Niveaudichte im betrachteten Energiebereich eine Konstante ist. (Für nichtkonstantes g() hätte
man den Nullpunkt der Energieskala nicht in die Mitte des betrachteten Energiebereichs
legen dürfen; wegen der vielen Näherungen, die ohnehin schon gemacht worden sind, lohnt
sich die Diskussion solcher Feinheiten aber hier kaum mehr.)
Die Bestimmung des Parameters 4
Ähnlich wie oben bestimmen wir jetzt
†
D(k) = ψBCS |c−k ck |ψBCS = uk vk ψBCS |α−k α−k
|ψBCS = uk vk ;
für 4 erhält man so die Konsistenzbedingung
4=W
0
X
k
0
0
1 X
4
1 X
p
sin θk = W
.
D(k) = W
2 + 2
2
2
4
k
k
k
Dies führt zu der Bestimmungsgleichung
Z +~ω0
d
1
~ω0
p
1 = W g(F )
= W g(F ) arsinh
2
4
42 + 2
−~ω0
mit der Lösung
~ω0
≈ 2~ω0 e−1/W g(F ) ,
1
sinh g(F )W
4=
was bis auf den Faktor 2 im Exponenten mit dem Ausdruck für die Bindungsenergie eines
Cooperpaares übereinstimmt;
genaue Übereinstimmung wäre ohnehin nicht zu erwarten,
weil der Zustand |ψBCS einen ganz anderen ”Hintergrund” für die Cooperpaare bildet als
der Zustand |0HF .
Bestimmung der Grundzustandsenergie
Als letztes müssen wir noch verifizieren, dass der Zustand |ψBCS
auch wirklich einen
niedrigeren Erwartungswert der Energie hat als der Zustand |0HF . Dazu berechnen wir
ψBCS |Hred |ψBCS =
0
0
X
X
†
†
c†k c†−k c−k0 ck0 |ψBCS
=
k ψBCS |ck ck + c−k c−k |ψBCS − W ψBCS |
kk0
k
=2
0
X
k
k vk2
−W
0
X
kk0
uk vk u v = 2
k0
k0
0
X
k
k vk2
42
−
,
W
(4.5)
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
82
wobei die obigen Zwischenergebnisse aus der Bestimmung von 4 und der mittleren Teilchenzahl benützt wurden. Der obige Ausdruck muss verglichen werden mit
E0,HF =
X
k <0
2k = −
0
X
k
|k | .
Für den ersten Term in (4.5) erhält man mit Hilfe des Ausdrucks für vk2 auf S. 79
2
0
X
k vk2
=
0
X
k
k
k
k
1−
λk
= −g(F )
Z
+~ω0
d p
−~ω0
2
2 + 42
,
weil der Mittelwert von k verschwindet. Für den Energieunterschied
Eg = EBCS − E0,HF
findet man
Eg = 2g(F )
Z
(
~ω0
d − p
0
2
)
2 + 42
−
42
.
W
Auswerten des Integrals und Einsetzen der obigen Beziehung zwischen 4 und W liefert
letztendlich
s
)
(
2
4
2g(F )~2 ω 2
1
− g(F )42 .
Eg = g(F )~2 ω02 1 − 1 + 2 2 = − 2/g( )W 0 ∼
=
F
~ ω0
e
−1
2
Das Ergebnis ist also für alle Werte von W negativ! Nach der hier behandelten einfachen
Theorie wird ein Metall also immer supraleitend, wenn für ein noch so kleines Energiegebiet
die attraktive, von Phononen vermittelte, Wechselwirkung zwischen den Elektronen größer
ist als die Coulombabstoßung.
Angeregte Zustände; die Energielücke
Die niedrigsten angeregten Zustände erhält man durch Anwendung der Erzeuger αk† für
Quasiteilchen auf den Grundzustand |ψBCS . Der so erhaltene Zustand ist
00 Y
αk† |ψBCS = uk c†k − vk c−k uk + vk c†k c†−k
uk0 + vk0 c†k0 c†−k0 |{0}
k0
= c†k
00 Y
k0
uk0 + vk0 c†k0 c†−k0 |{0} ,
Q
wobei das Symbol 00k0 ein Produkt über alle k0 6= k im betrachteten Band von Energiewerten bezeichnet. Die Energie des so erhaltenen Zustands liegt um λk oberhalb der
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
83
Grundzustandsenergie. Allerdings lässt sich der obige Zustand nicht über einen physikalischen Mechanismus anregen; jede Störung ist bilinear in den ck und c†k , und deshalb auch
in den αk und αk† . Die tatsächlich anregbaren Zustände haben die Form
αk† αk† 0 |ψBCS
=
c†k c†k0
000 Y
vk00 c†k00 c†−k00
uk00 +
k00
|{0}
mit der Zusatzenergie λk + λk0 , bzw.
†
|ψBCS
αk† α−k
=
uk c†k c†k
− vk
00 Y
u +v
k0
k0
c†k0 c†−k0
k0
|{0}
mit der Zusatzenergie 2λk . Die obige Rechnung überzeugt noch nicht ganz; eigentlich sollten wir nur Zustände mit derselben mittleren Teilchenzahl vergleichen. Dies lässt sich durch
eine geringfügige Änderung der uk0 und vk0 , die einer Verschiebung des Referenzniveaus
für die Energie der Ordnung N −1 entspricht, erreichen. (Vgl. die Änderung des chemischen
Potentials mit der Temperatur für das ideale Fermigas im Skriptum Thermodynamik und
Statistische Physik.) Es lässt sich zeigen, dass diese Korrektur nur zu Modifikationen der
Ordnung N −1 in den Anregungsenergien führt. Wir haben also gesehen, dass Anregungen
mit Energien kleiner als 24 nicht möglich sind. Diese so genannte Energielücke
ist experimentell gut bestätigt, und sie ist wesentlich für das Verständnis der elektromagnetischen Eigenschaften des Supraleiters.
Elektromagnetische Eigenschaften von Supraleitern
Von den Brüdern F. und H. London wurden schon 1935 zur Beschreibung des elektromagnetischen Verhaltens von Supraleitern für T TC die Gleichungen
E=
∂
(ΛJs )
∂t
B = −c ∇×(ΛJs )
(4.6)
vorgeschlagen. Dabei bezeichnet Js den Strom und Λ ist eine Konstante, die wegen
∇×E +
1 ∂B
=0
c ∂t
in beiden Gleichungen gleich gewählt werden soll. Die erste der Gleichungen (4.6) besagt,
dass der Strom ohne Dissipation fließt. Feld und Strom haben immer einen Phasenunterschied von 90◦ . Aus der zweiten Gleichung schließt man mit Hilfe der vierten Maxwellgleichung
∇×B =
4π
Js
c
⇒ ∇2 B =
4πB
B
≡ 2;
2
Λc
λL
Diese Gleichung besagt, dass das B-Feld im Inneren des Supraleiters auf einer Längenskala
λL abklingen muss (der Meißner-Ochsenfeld-Effekt). Weil λL experimentell die Größenordnung µm hat, heißt dies, dass ein Magnetfeld in einen Supraleiter kaum eindringen kann.
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
84
Andererseits kostet das Austreiben des Feldes (Kompression der Feldlinien) Energie, und
es wird ersichtlich, dass genügend hohe Magnetfelder die Supraleitung zerstören.
Für rein transversale Felder (und in der Coulomb-Eichung) lassen sich die Gleichungen
(4.6) zusammenfassen zu
Js (r) = −
1
A(r).
Λc
(4.7)
Letztere Gleichung werden wir jetzt zum Schluss unseres Kapitels über Supraleitung aus
der BCS-Theorie herleiten.
Mikroskopische Herleitung der London-Gleichung
Wir werden die London-Gleichung für langwellige stationäre transversale Felder herleiten
A(r) = Aq eiqr ;
qAq = 0.
Die elektrische Stromdichte wird im Formalismus der quantisierten Felder dargestellt von
dem Operator
X e~ Js (r) =
ψ † (r, σ)∇ψ(r, σ) − ψ(r, σ)∇ψ † (r, σ)
2mi
σ
2 X
e
−
ψ † (r, σ)A(r)ψ(r, σ) = JP (r) + JD (r),
mc σ
wobei die Operatoren JP und JD als paramagnetische bzw. diamagnetische Stromdichte bezeichnet werden. Die obige Form für den Stromdichteoperator folgt direkt aus dem
Operator
e e~
e2
e p− A =
∇−
A
j = ev =
m
c
im
mc
der normalen Ein-Teilchen-Quantenmechanik. Durch Einsetzen der Modenentwicklungen
für ψ und ψ † können wir JP und JD in den ckσ und c†kσ ausdrücken. Wir werden dabei
die Blochfunktionen uk (r) durch eins ersetzen; durch diese Prozedur erhält man über die
Einheitszelle gemittelte Stromdichten (das Überlappintegral der verschiedenen auftretenden uk (r) geht nach eins im Limes q → 0). Die so erhaltenen Ausdrücke sind
JP (r) =
e~ X †
0
ck+q0 ,σ ckσ e−iq r (2k + q0 ) ;
2mV kq0 σ
JD (r) = −
e2 X †
0
ck+q0 ,σ ckσ e−iq r A(r).
mcV kq0 σ
Die makroskopisch relevanten Größen sind die Erwartungswerte dieser Operatoren im
(durch das äußere Feld möglicherweise geänderten) Vielteilchenzustand
des Systems, ins
besondere bei T = 0, wo das ungestörte System im Zustand |ψBCS ist.
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
85
Die diamagnetische Stromdichte ist selbst linear im äußeren Feld; zurBerechnung der
im Feld linearen Antwort reicht es also aus, den Erwartungswert im |ψBCS zu bilden. Dies
impliziert, dass nur Terme mit q0 = 0 in der Summe überleben, wie man durch Zerlegen
†
der c†kσ und ckσ nach den α±k und α±k
leicht sieht. Das Ergebnis ist
X †
e2 Ns
e2
A(r) ψBCS |
A(r),
jD (r) = ψBCS |JD |ψBCS = −
ckσ ckσ |ψBCS = −
mcV
mcV
kσ
wobei Ns die Zahl der in Cooper-Paaren gebundenen Elektronen ist, also die Zahl der
Niveaus zwischen F − ~ω0 und F . Die diamagnetische Stromdichte allein hat also genau
die für die London-Gleichung erforderliche Form, wobei noch gilt
Λ=
m
ns e2
oder
λ2L =
mc2
,
4πns e2
mit ns = NVs die Dichte der an der Supraleitung beteiligten Elektronen.
Zur Berechnung der paramagnetischen Stromdichte brauchen wir zuerst die Änderung
des Grundzustandes durch die Störung
Z
XZ
e
e~ X
0
†
dr ψ (r) A(r)p ψ(r) = −
dr c†k+q0 ,σ ckσ A(r)k e−iq r ,
H1 = −
mc
mcV kq0 σ
σ
wobei wir wieder die uk0 (r) durch eins ersetzt haben. Einsetzen der speziellen Form von
A(r) ergibt
H1 = −
e~ X †
c
ckσ kAq .
mc kσ k+q,σ
(4.8)
Weil dieser Störterm nicht auf die Spins wirkt, können nur Paare von Quasiteilchen mit
entgegengesetzten Spins angeregt werden. (Der Operator αk† erhöht den Spin um ~/2,
†
während α−k
ihn um ~/2 erniedrigt.) Der gestörte Zustand hat also die Form
X
†
2
|ψA = |ψBCS + e
f (k0 )αk† 0 +q α−k
0 |ψBCS + O(e ),
k0
und die stationäre Störungsrechnung ergibt für die Koeffizienten
f (k) =
1
ψBCS |α−k αk+q H1 |ψBCS .
e (λk + λk+q )
Zum Matrixelement tragen zwei Terme in (4.8) bei:
†
†
c†k+q,↑ ck↑ |ψBCS = uk+q vk αk+q
α−k
|ψBCS
und
†
†
c†−k,↓ c−k−q,↓ |ψBCS = uk vk+q αk+q
α−k
|ψBCS ,
KAPITEL 3. QUANTENTHEORIE VON FERMIONFELDERN
86
wobei die Beziehungen u−k0 = uk0 ; v−k0 = −vk0 benützt wurden. Einsetzen dieser Beziehungen liefert
f (k) =
~
[kAq uk+q vk − (k + q)Aq uk vk+q ] ,
mc (λk + λk+q )
was sich wegen qAq = 0 reduziert zu
f (k) =
~kAq
~kAq
1
[uk+q vk − uk vk+q ] =
sin (θk − θk+q ) . (4.9)
mc (λk + λk+q )
mc (λk + λk+q )
2
Für q → 0 geht also der Zähler des Ausdrucks für f (k) nach Null, während der Nenner
endlich bleibt. Dies bedeutet aber, dass sämtliche f (k) für q → 0 verschwinden, und damit
der Erwartungswert
der paramagnetischen Stromdichte. (Der Erwartungswert von JP (r)
in |ψBCS verschwindet, wie man leicht zeigt.)
Damit ist gezeigt worden, dass der einzige Beitrag zur von einem Feld induzierten
Stromdichte der diamagnetische Beitrag ist, der die Londongleichung erfüllt. Auf ähnliche
Weise zeigt man, dass der B~σ -Term, der zu H1 noch hätte addiert werden müssen, und
der in normalen Metallen zur paramagnetischen Antwort beiträgt, auch keine Paare von
Quasiteilchen im Limes q → 0 anregen kann. In normalen Metallen gibt es elementare
Anregungen mit beliebig niedriger Energie. Die zu f (k) analogen Ausdrücke verschwinden dann im Limes q → 0 nicht, weil sowohl Zähler als auch Nenner des betreffenden
Ausdrucks verschwinden, und deren Quotient endlich bleibt. Man findet typischerweise,
dass die paramagnetische Stromdichte die diamagnetische weitgehend kompensiert, und es
bleiben nur kleine Nettoeffekte übrig.
Zum Schluss dieser Ausführungen soll noch betont werden, dass sämtliche in diesem
Abschnitt erhaltenen Ergebnisse auch in einer eichinvarianten Weise erhalten werden
können. Das Verhalten der ganzen Theorie unter Eichtransformationen ist aber recht kompliziert, weil die Feldoperatoren, und damit auch die Größen D(k) auf S. 78 ortsabhängige
Phasenfaktoren erhalten, und damit auch |ψBCS selbst keine eichinvariante Größe ist. Für
eine Diskussion siehe z.B. G. Rickayzen, Theory of Superconductivity, §6.4, oder Kittel, S.
172-177.
Kapitel 4
Die Dirac-Gleichung
4.1
Die ”Herleitung” der Dirac-Gleichung
Die von Dirac vorgeschlagene relativistische Wellengleichung für das Elektron kann natürlich genausowenig ”hergeleitet” werden wie irgendeine andere fundamentale Gleichung in
der Physik (Newton-, Maxwell- oder Schrödingergleichung). Man kann höchstens versuchen, die postulierte Gleichung plausibel zu machen. Dabei werden wir in dieser Vorlesung
nicht den ursprünglich von Dirac gewählten Zugang nehmen, sondern eine von Feynman
propagierte Alternative, die auch im Buch von Sakurai verwendet wird. Als Einführung
betrachten wir zunächst eine zuerst von van der Waerden vorgeschlagene, alternative
Form der nichtrelativistischen Schrödingergleichung für ein Teilchen mit Spin 21 .
Ein übliches Argument zur Begründung der Schrödingergleichung geht aus von der
Beziehung
E=
p2
+ V (r)
2m
und führt die Substitution
E
→
i~
∂
∂t
p
→
−i~∇
durch. Dies führt zur Schrödingergleichung
~2 2
∂
∇ + V (r) ψ.
i~ ψ = Hψ = −
∂t
2m
Für ein Teilchen mit Spin
1
2
gibt es aber die äquivalente Darstellung
(~σ p)(~σ p)
p2
=
,
2m
2m
die mittels der Identität
(~σ A) (~σ B) = AB + i~σ (A × B)
87
KAPITEL 4. DIE DIRAC-GLEICHUNG
88
leicht zu überprüfen ist. Aus der obigen Identität geht aber auch hervor, dass die Äquivalenz
verloren geht nach der Substitution
p
e
→ p − A(r);
c
die zweite Alternative führt dann zu
1 e e ~σ p − A ~σ p − A + V (r)
2m
c
c
1 i h
e e i
e 2
=
p− A +
~σ p − A × p − A + V (r),
2m
c
2m
c
c
was mittels der Identität
p × A + A × p = −i~( ∇×A)
in der Form
i2
1 h
e
e~
p − A(r) −
~σ B(r) + V (r)
2m
c
2mc
(1.1)
geschrieben werden kann. Der Zusatzterm
−
e~
e
~σ B = − SB,
2mc
mc
der in der üblichen Behandlung ”von Hand” eingesetzt werden muss, wird also in der
Formulierung von van der Waerden und Feynman automatisch mitgeliefert, inklusive des
Wertes 2 für das gyromagnetische Verhältnis des Elektrons. Der Hamiltonoperator (1.1)
wirkt selbstverständlich auf eine zweikomponentige Wellenfunktion des Elektrons.
Die freie Dirac-Gleichung
Ganz analog zum Vorhergehenden kann man für die relativistische Energie-Impuls-Beziehung
eines freien Teilchens mit Spin 12 schreiben
2
E
E
E
2
−p =
− ~σ p
+ ~σ p = m2 c2 .
c
c
c
Dies führt zu einer Wellengleichung für eine zweikomponentige Wellenfunktion ψ der
Form
i~ ∂
i~ ∂
+ i~~σ ∇
− i~~σ ∇ ψ = (mc)2 ψ.
c ∂t
c ∂t
Im Gegensatz zur nichtrelativistischen Schrödingergleichung ist dies eine Differentialgleichung zweiter Ordnung bezüglich der Zeit. Eine Reduktion auf Differentialgleichungen
KAPITEL 4. DIE DIRAC-GLEICHUNG
89
erster Ordnung ist aber ohne weiteres möglich durch Verdopplung der Zahl der Variablen: Falls wir definieren
ψ (L) ≡ ψ
ψ (R) ≡
i~
(∂0 − ~σ ∇) ψ
mc
mit
∂0 ≡
1∂
,
c ∂t
so gehorcht das Paar zweikomponentiger Wellenfunktionen ψ (R) , ψ (L) dem Gleichungssystem
i~ [∂0 − ~σ ∇] ψ (L) = mcψ (R) ;
(1.2)
i~ [∂0 + ~σ ∇] ψ (R) = mcψ (L) .
Für masselose Spin- 21 -Teilchen (Neutrinos) erweist sich die Variablenverdopplung als überflüssig; solche Teilchen können durch zweikomponentige Wellenfunktionen dargestellt werden, die einer Differentialgleichung erster Ordnung gehorchen. Es sind im Prinzip zwei
Arten von Neutrinos denkbar: Solche vom Typ ψ (L) , für die Spin und Impuls immer antiparallel stehen, und solche vom Typ ψ (R) , für die Spin und Impuls immer parallel stehen.
In der Natur kommen nur ”linkshändige” Neutrinos vom Typ ψ (L) vor (genauer gesagt, nur
solche Neutrinos wechselwirken mit normaler Materie oder Antimaterie über die schwache Wechselwirkung. Rechtshändige Neutrinos würden im Prinzip über ihre Energiedichte
zum Krümmungsradius des Weltalls beitragen, aber die Astrophysik ist noch weit davon
entfernt, solche Effekte messen zu können).
Um die Gleichungen (1.2) in die von Dirac angegebene Form zu bringen, bilden wir
zuerst Summe und Differenz der Größen ψ (L) und ψ (R) :
ψ (A) ≡ ψ (L) + ψ (R)
ψ (B) ≡ ψ (R) − ψ (L) .
Diese Größen erfüllen das Gleichungssystem
i~ ~σ ∇ψ (B) + ∂0 ψ (A) = mcψ (A)
i~ ~σ ∇ψ (A) + ∂0 ψ (B) = −mcψ (B)
oder, zusammengefasst zu einem vierdimensionalen System
(A) (A) −∂0 −σ∇
ψ
ψ
i~
= −mc
.
σ∇
∂0
ψ (B)
ψ (B)
Eine etwas kompaktere Schreibweise entsteht mit Hilfe der Definitionen
0 −iσk
I 0
γk =
k = 1, 2, 3
γ4 =
,
iσk
0
0 −I
90
KAPITEL 4. DIE DIRAC-GLEICHUNG
wobei I die zweidimensionale Einheitsmatrix und 0 die zweidimensionale Nullmatrix darstellt. Die obigen Definitionen führen zum Gleichungssystem
∂
mc
~γ ∇ + γ4
ψ+
ψ = 0;
x4 = ict,
∂x4
~
oder noch kompakter (mit Einstein-Konvention)
∂
mc
γµ
+
ψ = 0.
∂xµ
~
(1.3)
Hier ist die Größe ψ ein vierdimensionales Objekt, das als Spinor bezeichnet wird. Eine
etwas explizitere Darstellung von (1.3) ist
4 X
4 X
µ=1 β=1
(γµ )αβ
∂
mc
+
δαβ ψβ = 0.
∂xµ
~
(α = 1, . . . , 4).
Die Matrizen γµ erfüllen die Antivertauschbeziehungen
{γµ , γν } = 2δµν I4 ,
(1.4)
die man aus der expliziten Darstellung leicht überprüfen kann (die Größe I4 bezeichnet die
4-dimensionale Einheitsmatrix):
0 −iσk
0 −iσl
0 −iσl
0 −iσk
{γk , γl } =
+
iσk
0
iσl
0
iσl
0
iσk
0
{σk , σl }
0
I 0
=
= 2δkl
,
0
{σk , σl }
0 I
usw. Wie zuerst von Pauli gezeigt wurde, bestimmen die Beziehungen (1.4) die 4-dimensionalen
Matrizen γµ bis auf eine Ähnlichkeitstransformation:
0 0
γµ , γν = 2δµν I4 ⇐⇒ γµ0 = Sγµ S−1
mit irgendeiner nichtsingulären Matrix S. Aus diesem Theorem folgt sofort, dass man aus
jeder Lösung ψ der Gleichung (1.3) eine Lösung ψ 0 ≡ Sψ der Gleichung
mc
0 ∂
+
ψ0 = 0
γµ
∂xµ
~
konstruieren kann. Der physikalische Inhalt der Dirac-Gleichung wird deshalb von einer
Änderung der Darstellung der γ-Matrizen nicht beeinträchtigt, und man findet in der Literatur eine Menge solcher Darstellungen, worauf wir hier nicht näher eingehen werden. Wir
bemerken weiters noch, dass mit unserer Wahl der γµ diese hermitesch und spurlos sind.
Letztere Eigenschaft bleibt unter Ähnlichkeitstransformationen erhalten; die Hermitizität
91
KAPITEL 4. DIE DIRAC-GLEICHUNG
ebenso, wenn S unitär gewählt wird. Zum Schluss erwähnen wir noch, dass die Darstellungsunabhängigkeit der Dirac-Gleichung in Anwesenheit eines elektromagnetischen Feldes
erhalten bleibt, wie man nach der Substitution
~ ∂
~ ∂
e
−→
− Aµ ,
i ∂xµ
i ∂xµ c
leicht sieht.
Die Gleichung (1.3) kann durch Multiplikation von links mit γ4 in die vertraute Form
i~
∂
ψ = HD ψ
∂t
(1.5)
gebracht werden. Für den Hamiltonoperator findet man so
HD = −ic~~
α∇ + βmc2
(1.6)
mit
I 0
;
0 −I
β = γ4 =
0 σk
.
σk 0
αk = iγ4 γk =
Die Form (1.6) ist die von Dirac ursprünglich vorgeschlagene.
Wahrscheinlichkeitsdichte und Wahrscheinlichkeitsstrom
Wir werden mit einer Diskussion der physikalischen Interpretation von ψ und seinen Komponenten noch etwas warten, bis wir einige einfache Lösungen der Dirac-Gleichung diskutiert haben. Es liegt aber nahe anzusetzen, dass die Größe
X
ψα∗ (r, t)ψα (r, t)d3 r
ψ † (r, t)ψ(r, t)d3 r ≡
α
die Wahrscheinlichkeit darstellt, zur Zeit t ein Teilchen im Volumen d3 r um r anzutreffen.
Wir werden später sehen, dass diese Interpretation nicht ganz unproblematisch ist, aber
wir zeigen jetzt als erstes, dass es in der Dirac-Theorie eine Kontinuitätsgleichung für
die Größe ψ † ψ gibt. Aus der Dirac-Gleichung folgt für ψ †
∂
mc †
∂ †
ψ γk + ∗ ψ † γ4 +
ψ = 0.
∂xk
∂x4
~
Multiplikation von rechts mit γ4 und Ausnützen von
∂
∂
∂
=
=−
∗
∗
∂x4
∂(ict)
∂x4
liefert für die Größe ψ̄ ≡ ψ † γ4 die adjungierte Gleichung
mc
∂
ψ̄γµ +
ψ̄ = 0,
∂xµ
~
KAPITEL 4. DIE DIRAC-GLEICHUNG
92
wobei wir noch die Beziehung γµ γ4 = −γ4 γµ benutzt haben. Aus der obigen Gleichung und
der Dirac-Gleichung selbst folgt jetzt
∂
ψ̄γµ ψ = 0,
∂xµ
also eine Erhaltungsgröße für den Stromvektor
sµ = icψ̄γµ ψ = cψ † α
~ ψ, icψ † ψ .
Es liegt also nahe, die Größe
j = cψ † α
~ψ
als Wahrscheinlichkeitsstromdichte und ψ † ψ als Wahrscheinlichkeitsdichte zu interpretieren. Zur Absicherung dieser Interpretation sollte eigentlich noch gezeigt werden, dass sich
sµ unter Lorentztransformationen in der Tat wie eine Vektordichte transformiert. Dies ist
tatsächlich der Fall, aber der Beweis kann hier nicht gegeben werden (siehe Sakurai oder
Messiah). Weiters liegt es nahe, die Größe c~
α als Geschwindigkeitsoperator zu deuten,
was sich mit gewissen Einschränkungen als möglich erweisen wird. Zum Schluss bemerken
wir noch, dass die obige Form für sµ auch in Anwesenheit eines Viererpotentials Aµ ungeändert bleibt, wie man leicht nachprüft. Die Stromdichte in der Dirac-Theorie hat also
keine manifest diamagnetischen Anteile!
4.2
Nichtrelativistische Näherungen
In diesem Abschnitt diskutieren wir die Lösungen der Gleichung
∂
ie
mc
− Aµ γµ ψ +
ψ=0
∂xµ ~c
~
(2.1)
die harmonisch von der Zeit abhängen gemäß
ψ(r, t) = ψ(r, 0)e−iEt/~ ,
also stationäre Lösungen. Das Viererpotential Aµ ist dabei definiert als
Aµ ≡ (A, iA0 ) = (A, iΦ)
Die Gleichung (2.1) kann jetzt zerlegt werden in zwei Gleichungen für die Bestandteile ψ (A)
und ψ (B) :
h 1
e i
E − eA0 − mc2 ψ (A) ;
~σ p − A ψ (B) =
c
c
h e i (A) 1
~σ p − A ψ =
E − eA0 + mc2 ψ (B) .
c
c
KAPITEL 4. DIE DIRAC-GLEICHUNG
93
Mit Hilfe der zweiten Gleichung kann man ψ (B) eliminieren; so erhält man
h h (A)
e i
c2
e i (A)
2
ψ .
~σ p − A
~
σ
p
−
A
ψ
=
E
−
eA
−
mc
0
c
E − eA0 + mc2
c
Für nichtrelativistische Teilchen gilt
E ≈ mc2 ;
|eA0 | mc2 .
Es liegt also nahe, die nichtrelativistische Energie zu definieren als
E(NR) = E − mc2
und den Faktor in der Mitte der Gleichung für ψ (A) zu entwickeln gemäß
"
#
2mc2
1
1
E(NR) − eA0
c2
=
=
1−
+ . . . . (2.2)
E − eA0 + mc2
2m 2mc2 + E(NR) − eA0
2m
2mc2
Wenn man sich auf den ersten Term beschränkt, erhält man die Gleichung
1 e e ~σ p − A ~σ p − A ψ (A) = E(NR) − eA0 ψ (A) ,
2m
c
c
also genau die van-der-Waerden’sche Form der nichtrelativistischen stationären Schrödingergleichung für eine zweikomponentige Wellenfunktion; wie im vorhergehenden Abschnitt
gezeigt wurde, lässt sie sich schreiben als
e 2
e~
1 p− A −
~σ B + eA0 ψ (A) = E(NR) ψ (A) .
2m
c
2mc
(Für eine lineare Superposition von stationären Lösungen, deren Eigenwerte alle die Ungleichung E(NR) mc2 erfüllen, gilt die zeitabhängige Schrödingergleichung für die Größe
ψ (NR) (r, t) = ψ (A) (r, t)eimc
2 t/~
;
der zusätzliche Phasenfaktor ist für die physikalische Interpretation ohne Bedeutung; wir
haben damit also aus der Dirac-Gleichung die Schrödingergleichung hergeleitet zusammen
mit der Bedingung für ihre Gültigkeit.)
Relativistische Korrekturen für den elektrostatischen Fall
Als nächstes werden wir den Korrekturterm in (2.2) mit berücksichtigen; dabei werden
wir uns aber der Einfachheit halber auf den Fall A = 0 beschränken. Die so entstandene
Gleichung lässt sich schreiben als
(NR)
HA
ψ (A) = E(NR) ψ (A)
94
KAPITEL 4. DIE DIRAC-GLEICHUNG
mit
(NR)
HA
1
= (~σ p)
2m
E(NR) − eA0
1−
+ ...
2mc2
!
(~σ p) + eA0 .
Auf den ersten Blick sieht diese Gleichung ganz vernünftig aus; bei näherer Betrachtung
sieht man aber (mindestens) drei Schwierigkeiten:
(NR)
1 Der Operator HA
(NR)
enthält den Eigenwert EA
.
(NR)
2 Der Operator HA
ist nicht hermitesch; beim Ausarbeiten der (~σ p) sieht man, dass
(NR)
neben hermiteschen Termen ein Term i~Ep entsteht. Die Nichthermitizität von HA
ist nicht ohne weiteres fatal, aber sie macht lästige Umformulierungen der allgemeinen
Theorie erforderlich.
3 Die zweikomponentige Wellenfunktion ψ (A) ist nicht korrekt normiert; die korrekte Normierung lautet
Z
dr ψ (A)† ψ (A) + ψ (B)† ψ (B) = 1.
Bis zur betrachteten Ordnung gilt aber
ψ (B) ≈
~σ p (A)
ψ ,
2mc
weshalb wir die Normierungsbedingungen für ψ (A) in der Form
Z
p2
(A)†
(A)
dr ψ
1+
ψ
≈1
4m2 c2
schreiben können.
Wie wir gleich zeigen werden, lassen sich sämtliche Schwierigkeiten beheben, und zwar
durch die Transformation
p2
(A)
ψ (A) .
Ψ = Ωψ ≡ 1 +
8m2 c2
Die zweikomponentige Wellenfunktion Ψ ist offensichtlich bis zur betrachteten Ordnung
korrekt normiert, und die Gleichung
(NR)
Ω−1 HA
Ω−1 Ψ = E(NR) Ω−2 Ψ
lautet bis auf Terme höherer Ordnung
"
2 2
p2
p
p
~σ p
+ eA0 −
,
+ eA0
−
2
2
2m
8m c
2m
2m
E(NR) − eA0
2mc2
!
#
~σ p Ψ = E
(NR)
1−
p2
4m2 c2
Ψ.
KAPITEL 4. DIE DIRAC-GLEICHUNG
95
oder
o
p2
p4
1 n 2 (NR)
+ eA0 −
p
,
E
−
eA
+
0
2m
8m3 c2 8m2 c2
i
−2 (~σ p) E(NR) − eA0 (~σ p) Ψ = E(NR) Ψ.
Der letzte Term in den eckigen Klammern lässt sich umformen mittels der Identität
2ABA = A2 , B − [A, [A, B]]
(mit A = ~σ p und B = E(NR) − eA0 ). Der erste Term kompensiert genau den vierten Term
in den eckigen Klammern. Weil die Zahl E(NR) zum Doppelkommutator nicht beiträgt, ist
damit auch die Abhängigkeit vom Eigenwert E(NR) eliminiert worden. Der Doppelkommutator lässt sich weiter vereinfachen mit Hilfe der Identitäten
[~σ p, −eA0 ] = −ie~~σ E
[~σ p, −ie~~σ E] = −e~2 ∇E − 2e~~σ (E × p)
bei deren Herleitung auch ∇A0 = −E und ∇×E = 0 verwendet wurden. Einsetzen der
Ergebnisse sämtlicher Umformungen liefert
2
p4
e~~σ (E × p)
e~2
p
+ eA0 −
−
−
∇E Ψ = E(NR) Ψ.
(2.3)
2m
8m3 c2
4m2 c2
8m2 c2
Die ersten zwei Terme in (2.3) sind bekannt; der dritte Terme ist die erste Korrektur zur
kinetischen Energie, die man auch erhalten würde mittels der Taylorentwicklung
q
p2
p4
(mc2 )2 + p2 c2 − mc2 =
−
+ ...
.
2m 8m3 c2
Der vierte Term liefert die Spin-Bahn-Kopplung: Ein Elektron, das sich im Feld E bewegt,
”sieht” in seinem Ruhesystem infolge der Lorentztransformation ein Magnetfeld, welches
an seinen Spin ankoppelt. Für ein zentralsymmetrisches Potential eA0 = V (r) erhält man
die vertraute Form
e~
~
1 dV
1 dV
− 2 2 ~σ (E × p) = − 2 2 −
~σ (r × p) =
S L.
4m c
4m c
r dr
2m2 c2 r dr
Der letzte Term
−
e~2
e~2
∇E
=
∇2 A0 ,
8m2 c2
8m2 c2
der als Darwin-Term bezeichnet wird, kann mit der potentiellen Energie eA0 zusammen
genommen werden. Er besagt dann, dass das Elektron nicht das Potential am genauen Ort
~
r spürt, sondern den Mittelwert über einen Bereich der Abmessung mc
= 3, 9 · 10−11 cm.
96
KAPITEL 4. DIE DIRAC-GLEICHUNG
Auf dieses Phänomen werden wir später im Zusammenhang mit der so genannten Zitterbewegung des Dirac-Elektrons noch zurückkommen.
Für das Wasserstoffatom gilt
∇E = 4πeδ(r)
und der Darwin-Term trägt nur für s-Zustände bei (im Gegensatz zur Spin-Bahn-Kopplung,
die nur für l 6= 0-Zustände von Bedeutung ist). Der Einfluss der Zusatzterme in (2.3) in erster Ordnung Störungstheorie lässt sich für das Wasserstoffatom explizit berechnen (Rechnungen in zweiter und höherer Ordnung sind nur sinnvoll, wenn auch höhere Korrekturen
(NR)
zu HA berücksichtigt werden). Die Energiewerte hängen nur von den Quantenzahlen n
und j ab und betragen
−e2 1
α2
1
3
,
Enj =
+
−
2a0 n2 n3 j + 12
4n
wobei a0 den Bohr’schen Radius und α0 die Feinstrukturkonstante darstellt. Ohne Beweis
erwähnen wir noch, dass sich die volle Dirac-Gleichung für das Wasserstoffatom auch exakt
lösen lässt; das Ergebnis ist (für Kernladung Z)

Enj
− 21


Z 2 α2


= mc 1 + 2 
q


2
j + 12 − Z 2 α2
n − j + 21 +
2
.
Wegen der Beziehung
1 2 2
e2
α mc =
2
2a0
liefert die Taylorentwicklung nach Potenzen von α2 bis auf einen additiven Faktor mc2 das
nichtrelativistische Ergebnis. Es ist bemerkenswert, dass in der Dirac-Theorie neben der
jz -Entartung auch noch ein Teil der l-Entartung erhalten bleibt. So sind z.B. die Zustände
2s1/2 und 2p1/2 immer noch entartet; diese Entartung wird erst durch die Wechselwirkung
mit dem Strahlungsfeld aufgehoben (siehe unsere Diskussion der Lamb-Verschiebung in
Kapitel 2.4).
Weiters ist noch zu bemerken, dass der exakte Ausdruck nur für Z ≤ 137 gilt; für höhere
Werte von Z treten formal komplexe Eigenwerte auf (instabile Niveaus). Stabile Kerne mit
Z > 137 kommen zwar in der Natur nicht vor, aber die Ergebnisse haben trotzdem eine gewisse Relevanz für die Beschreibung von Experimenten, in denen hochenergetische schwere
Kerne aufeinandergeschossen werden. Auf die physikalische Bedeutung der komplexen Eigenwerte werden wir kurz näher eingehen im Zusammenhang mit unserer Diskussion des
Klein’schen Paradoxons im nächsten Abschnitt.
97
KAPITEL 4. DIE DIRAC-GLEICHUNG
4.3
Lösungen der freien Dirac-Gleichung
In diesem Abschnitt diskutieren wir Lösungen der freien Dirac-Gleichung (Aµ = 0) der
Form einer ebenen Welle:
(A) ψ
i(pr−Et)/~ uA (p)
,
ψ(r, t) =
= Ne
uB (p)
ψ (B)
wobei N ein noch zu bestimmender Normierungsfaktor ist. Substitution in die Gleichungen
für ψ (A) und ψ (B) ergibt
uA (p) =
c
(~σ p) uB (p);
E − mc2
uB (p) =
c
(~σ p) uA (p).
E + mc2
(3.1)
Die Größen E und p erfüllen selbstverständlich die Beziehung
q
E = ± p2 c2 + (mc2 )2 .
Für jede Wahl des Vorzeichens existieren zwei linear unabhängige Lösungen. Insbesondere
für p2 m2 c2 gilt:
uA (p)
uB (p)
>
für E 0 .
<
Um zur korrekten Wahl des Vorzeichens für E zu gelangen, betrachten wir zuerst den
Fall p = 0. Dann muss gelten
γ4
∂
mc
ψ=− ψ
∂(ict)
~
oder expliziter
E I 0
mc uA (0)
uA (0)
−
=−
.
uB (0)
c~ 0 -I
~ uB (0)
Aus dieser Gleichung folgt sofort, dass gelten muss
E = mc2 ⇐⇒ uB (0) = 0;
E = −mc2 ⇐⇒ uA (0) = 0
Der vollständige Satz von Eigenspinoren
 
 
 
0
1
0






1
0
(3)
(2)
0

 
u
=
u(1) = 
u
=
0
1
0
0
0
0
u(4)
 
0
0

=
0
1
hat als zusätzliche Eigenschaft, dass er aufgebaut ist aus Eigenvektoren des Operators
γ1 γ2 − γ2 γ1
σ3 0
Σ3 =
=
,
0 σ3
2i
KAPITEL 4. DIE DIRAC-GLEICHUNG
98
der bis auf den Faktor ~2 den Spin des Dirac-Elektrons beschreibt. (Diese intuitiv plausible
Interpretation kann abgesichert werden durch Betrachtung des Transformationscharakters
der Dirac-Gleichung unter Drehungen. Dies wird in dieser Vorlesung nicht durchgeführt.)
Man wählt jetzt die Eigenspinoren u(1) (p) und u(2) (p) für E > 0 auch für p 6= 0 so,
dass gilt
(2)
(1)
0 0
0 1
;
;
uA (p) = N
uA (p) = N
1
0
für die Eigenspinoren u(3) (p) und u(4) (p) für E < 0 wählt man dagegen
(4)
(3)
0 0
0 1
.
;
uB (p) = N
uB (p) = N
1
0
Mit Hilfe der Darstellung
p3
p1 − ip2
~σ p =
p1 + ip2
−p3
erhält man so aus (3.1) für die vollständigen Eigenspinoren




1
0




0
1


u(1) (p) = N 0 
u(2) (p) = N 0 
 p3 c/(E+mc2 )  ;
(p1 −ip2 )c/(E+mc2 ) ;
(p1 +ip2 )c/(E+mc2 )
−p3 c/(E+mc2 )




−(p1 −ip2 )c/(|E|+mc2 )
−p3 c/(|E|+mc2 )
−(p1 +ip2 )c/(|E|+mc2 )
 p3 c/(|E|+mc2 ) 
(4)
0
;
.
u(3) (p) = N 0 
u
(p)
=
N




1
0
0
1
Man prüft leicht nach, dass für die so konstruierten Eigenspinoren gilt
u(r)† (p) u(s) (p) = 0
für r 6= s.
Die Normierung der Eigenspinoren ist weitgehend eine Konventionssache. Die am häufigsten verwendete Konvention ist
r
|E|
|E| + mc2
(r)†
(r)
0
⇒
N
=
;
u (p)u (p) =
mc2
2mc2
dies bedeutet, dass sich die Norm des Eigenspinors wie die vierte Komponente eines Vierervektors transformiert. Mit dieser Definition sind die normierten Eigenlösungen der DiracGleichung
s
mc2 (r)
ψ (r) (r, t) =
u (p) ei(pr−ηr |E|t)/~
|E| V
99
KAPITEL 4. DIE DIRAC-GLEICHUNG
mit
(
+1 für r = 1, 2;
ηr =
−1 für r = 3, 4.
Die Korrektheit der Wahl der Vorzeichen ηr für die Energie, die bisher nur über die Analogie
mit dem Fall p = 0 plausibel gemacht wurde, lässt sich auch mittels Substitution in die
Dirac-Gleichung überprüfen.
Wir bemerken noch, dass die Eigenspinoren u(r) (p) nur im Spezialfall p1 = p2 = 0
auch Eigenvektoren von Σ3 sind. Wie wir gleich sehen werden, ist nur die Komponente
des Spins parallel zu p eine Bewegungskonstante der freien Dirac-Gleichung. Dies stellt
einen wichtigen Unterschied zur nichtrelativistischen Theorie dar.
Im Limes V → ∞ erhält man für das Eigenwertspektrum der freien Dirac-Hamiltonfunktion
ein (zweifach) entartetes Kontinuum mit den zwei getrennten Bereichen
−∞ < E < −mc2
und
mc2 < E < ∞.
Das Fehlen einer unteren Schranke für die möglichen E-Werte stellt die größte Schwierigkeit bei der Interpretation der Dirac-Gleichung als Einteilchengleichung dar; eine nicht sehr
speziell gewählte Störung würde ein unbeschränktes Absinken der Energie des Elektrons
zur Folge haben. Damit würde die Stabilität der Materie, die gerade durch die Einführung
der ”normalen” Quantentheorie wiederhergestellt wurde, wieder verloren gehen. Ehe wir
im nächsten Abschnitt auf die Vorschläge zur Beseitigung dieser Schwierigkeit eingehen,
diskutieren wir kurz noch einige weitere Folgerungen aus der Dirac-Gleichung.
Observable und Bewegungskonstanten
Die Observablen für ein Diracteilchen lassen sich genauso wie für ein Schrödingerteilchen
aus den Basisoperatoren r, p und S konstruieren; lediglich für die Komponenten von S ist
in der Diractheorie eine andere Darstellung notwendig; auf S. 97 wurde die Darstellung
~1
~ σi 0
~
ijk γj γk =
Si = Σi =
2
2 2i
2 0 σi
vorgeschlagen, allerdings mit einer recht dürftigen Begründung. In der nachfolgenden Betrachtung werden wir die Dynamik dieser Observablen (im Heisenbergbild) etwas näher
betrachten. Die Bewegungsgleichung für eine Observable A lautet
dA
∂A
i
=
+ [H, A]
dt
∂t
~
mit
H = c~
αp + βmc2 .
Die Observable p vertauscht offensichtlich mit H und ist also auch in der Diractheorie für
ein freies Teilchen eine Bewegungskonstante.
KAPITEL 4. DIE DIRAC-GLEICHUNG
100
Die erste Überraschung tritt bei der Betrachtung des Drehimpulses auf. Dafür gilt
[H, L] = [c~
αp, r × p] =
~
cα
~ ×p
i
oder
dL
=cα
~ × p.
dt
Anders als in der Schrödingertheorie eines freien Teilchens mit Spin 12 ist der Drehimpuls
also keine Bewegunskonstante. Auch der Spin ist, wie schon aus der Konstruktion der
Eigenspinoren hervorging, keine Bewegungskonstante. Wegen
0 σi
σj 0
0 σk
[αi , Σj ] =
,
= 2iijk
;
σi 0
0 σj
σk 0
I 0
σi 0
[β, Σi ] =
,
=0
0 -I
0 σi
gilt
i
i
ic h
d
~ = −c α
S = [H, S] =
α
~ p, Σ
~ × p.
dt
~
2
Wir sehen also, dass wenigstens der Gesamtdrehimpuls
J=L+S
auch für das freie Diracteilchen eine Bewegungskonstante ist; dies gilt übrigens auch für
die Größe S · p oder für
S p̂ =
S·p
|p|
die sog. Helizität des Elektrons. Die Tatsache, dass J = L + S für unsere Wahl von S eine
Bewegungskonstante ist, ist natürlich umgekehrt ein starkes Argument für die Wahl von
~~
Σ als Darstellung für den Spinoperator S.
2
Als nächstes betrachten wir die Zeitentwicklung des Ortsoperators:
dr
i
ic
= [H, r] = [~
αp, r] = c α
~.
dt
~
~
Für den Geschwindigkeitsoperator erhalten wir also nicht etwa p/m, sondern c~
α. Weil jede
Komponente von α
~ nur die Eigenwerte ±1 hat, ist klar, dass ein Elektron nie in einem
Eigenzustand einer Komponente von α
~ sein kann (Lichtgeschwindigkeiten sind für Teilchen
mit endlicher Masse nicht erlaubt!). Formal betrachtet: die Eigenvektoren von αi haben
keinen endlichen Erwartungswert der Energie und können nicht experimentell präpariert
werden. Für den Operator α
~ erhält man die Bewegungsgleichung
d~
α
i
i
i
= [H, α
~ ] = (−2~
αH + {H, α
~ }) = (−2~
αH + 2cp) ,
dt
~
~
~
KAPITEL 4. DIE DIRAC-GLEICHUNG
101
wie man aus {αi , αj } = 2δij und {αi , β} = 0 sofort sieht. Die obige Operator-Differentialgleichung
hat die Lösung
cp cp −2iHt/~
α
~ (t) =
+ α
~ (0) −
e
,
H
H
wie man durch direkte Substitution sieht (bedenke [H, p] = 0). Der erste Term ist für einen
Eigenzustand von p genau die Gruppengeschwindigkeit dividiert durch c:
q
dE(p)
d
c2 p
2
vg ≡
=
± p2 c2 + (mc2 ) =
dp
dp
E(p)
(bemerke, dass für Zustände negativer Energie vg und p antiparallel stehen!). Der Zusatzterm stellt eine sehr hochfrequente, oszillierende Bewegung dar (minimale Frequenz
2mc2 /~ ' 1, 5 · 10+21 sec−1 ), die Zitterbewegung genannt wird.
Der Erwartungswert der Amplitude der Zitterbewegung verschwindet für Eigenzustände
von p; z.B. gilt
Z
dr ψp(1)† (r)αi ψp(1) (r) =

†


1
1

E + mc2 
0 
0 

 0 σi 
 V = cpi .




1
1
σ
0
2E V
E
i
c
c
~σ p
σp
2 ~
E+mc2
E+mc
0
0
Auf analoge Weise errechnet man die Erwartungswerte in den übrigen Eigenfunktionen.
Matrixelemente von αi zwischen Eigenfunktionen mit unterschiedlichem p verschwinden
trivialerweise (r-Integration), und man zeigt auch leicht
Z
Z
(1)†
(2)
dr ψp (r) αi ψp (r) = dr ψp(3)† (r) αi ψp(4) (r) = 0
Um eine nichtverschwindende Amplitude der Zitterbewegung zu erhalten, braucht man
also eine Linearkombination von Lösungen der freien Diracgleichung mit unterschiedlichen
Vorzeichen von E; durch Betrachten der führenden Komponenten sieht man z.B.
2 Z
p
(3)†
(1)
.
dr ψp (r) α3 ψ (r) = 1 + O
m2 c2
Eng mit dem Phänomen der Zitterbewegung verknüpft ist die Unmöglichkeit, ein Diracteilchen beliebig genau zu lokalisieren. Die Konstruktion einer Wellenfunktion vom Typ
ψ † (r) = (Φ∗ (r), 0, 0, 0)
führt nicht zum Ziel; in einer Zerlegung nach ebenen Wellen gemäß
Z
ψ(r) = dp c1 (p)u(1) (p) + c3 (p)u(3) (p) + c4 (p)u(4) (p) eipr/~
KAPITEL 4. DIE DIRAC-GLEICHUNG
102
muss gelten
c3 (p)
−p3 c
=
;
c1 (p)
|E(p)| + mc2
− (p1 − ip2 ) c
c4 (p)
=
.
c1 (p)
|E(p)| + mc2
Das Auftreten von Wellenvektoren mit p ∼ mc, die für eine Lokalisierung auf Gebiete 4x ∼
~/mc notwendig sind, hat also automatisch eine starke Beimischung von Komponenten
mit negativen Energien, also eine ausgeprägte Zitterbewegung, zur Folge; letztere zerstört
dann sofort wieder die Lokalisierung. Newton und Wigner konnten zeigen, dass auch
die Bildung eines Wellenpaketes, welches nur Komponenten positiver Energie enthält, nie
zu einer Lokalisierung schärfer als 4x ∼ ~/mc führen kann. Weil die Eigenfunktionen
der freien Diracgleichung mit E > 0 nicht vollständig sind, ist auch nicht zu erwarten,
dass die Eigenfunktionen zu E > 0 eines Diracteilchens in einem äußeren Potential aus
einer linearen Superposition von Ebenen-Wellen-Lösungen mit E > 0 aufzubauen sind.
Dies erklärt das Auftreten des Darwin-Terms in der ersten relativistischen Korrektur zur
Schrödingergleichung, der ja als eine Verschmierung der Position des Elektrons über einen
Bereich ~/mc gedeutet werden konnte.
Stückweise konstante Potentiale; das Klein’sche Paradoxon
Der Fall eines stückweise konstanten Potentials, welches nur von einer Raumkoordinate
abhängt, ist auch für die Diracgleichung der nächst einfache exakt lösbare Fall. Weil die
Diracgleichung eine Gleichung erster Ordnung in den Raumableitungen ist, braucht man
nur Stetigkeit der vierkomponentigen Wellenfunktionen zu verlangen, nicht aber deren
Ableitungen. Wegen der Verdopplung der Komponentenzahl gegenüber der nichtrelativistischen Theorie bleibt aber die Zahl der so erhaltenen Anschlussbedingungen die gleiche.
Die Energie-Impuls-Beziehung in einem Bereich mit Potential V = eA0 folgt z.B. aus der
Beziehung
(~σ p)
und lautet
(A)
c2
(A)
2
(~
σ
p)
ψ
=
E
−
V
−
mc
ψ
E − V + mc2
p2 c2 = E − V + mc2
E − V − mc2 .
Diese Gleichung hat reelle Lösungen für
E > V + mc2
oder
E < V − mc2 .
und imaginäre Lösungen (evaneszente Wellen) für die ”Bandlücke”
V − mc2 < E < V + mc2 .
Wir werden hier keine expliziten Rechnungen durchführen. Diese sind im Prinzip nicht
schwierig, dafür aber etwas langwierig; explizite Rechnungen findet man z.B. in W. Greiner,
Theoretische Physik, Band 6. Das qualitative Verhalten ist aber aus den obigen Ergebnissen
leicht einsichtig zu machen.
103
KAPITEL 4. DIE DIRAC-GLEICHUNG
Kastenpotentiale
(
V0 für |z| < a
V=
0
für |z| > a.
Für |V| < 2mc2 ergibt sich folgende Situation (Skizze für V<0)
E
mc2
mc2 +V
-a
a
Z
-mc2
-mc2 -V
• Im Energiebereich E > mc2 hat man ein kontinuierliches Spektrum (Streuzustände)
• Im Bereich mc2 + V < E < mc2 hat man einige diskrete, in dem Kasten lokalisierte,
Niveaus.
• Im Bereich −mc2 < E < mc2 + V gibt es keine Zustände.
• Im Bereich E < −mc2 gibt es wieder nur ein kontinuierliches Spektrum. Für −mc2 −
V < E < −mc2 sind die verallgemeinerten Eigenfunktionen im Bereich |z| < a
evaneszent: Die ebenen Wellen negativer Energie tunneln durch das für sie abstoßend
wirkende Potential hindurch.
Beim Anwachsen von |V| spalten sich die gebundenen Zustände vom Kontinuum der
Zustände mit E > 0 ab. Für V > 0 ”entstehen” hingegen gebundene Zustände aus dem
Kontinuum der Zustände mit negativer Energie.
Für |V| > 2mc2 wird das Verhalten qualitativ anders:
104
KAPITEL 4. DIE DIRAC-GLEICHUNG
E
Z=-a
Z=a
Z
mc2
-mc2
mc2 +V
-mc2 +V
Für mc2 + V < E < −mc2 hat man jetzt ein kontinuierliches Spektrum, allerdings mit
Resonanzen im Reflexionskoeffizienten, deren Lagen in Abhängigkeit von V sich stetig
mit den Lagen gebundener Zustände verbinden lässt; die gebundenen Zustände werden
instabil beim ”Eintauchen” in das Kontinuum der Zustände negativer Energie (vgl. das
Ergebnis für das Coulombproblem mit Zα > 1; dort tritt aber ein ”Zusammenbruch” auf
für den Energiewert E1,1/2 = 0; dies ist aber eine Besonderheit des singulären Potentials.
Nach Abschneiden des Potentials tritt die Instabilität erst bei E1,1/2 = −mc2 auf).
Ähnlich paradoxe Ergebnisse erhält man für Streuung an einer Potentialstufe:
V(z) = V0 θ(z).
Für V0 < 2mc2 erhält man teilweise Reflexion für E(p) > V0 + mc2 und Totalreflexion für
E(p) < V0 + mc2 . Für V0 > 2mc2 tritt aber die skizzierte Lage auf:
105
KAPITEL 4. DIE DIRAC-GLEICHUNG
E
V_0+mc2
V_0-mc2
mc2
0
Z
Für E(p) < V0 − mc2 wird das Potential wieder transparent; es lässt sich eine Lösung
konstruieren aus einer einlaufenden und einer reflektierten Welle für z < 0 und einer nach
rechts auslaufenden Welle (mit pZ < 0 wegen des anomalen Vorzeichens der Gruppengeschwindigkeit im unteren Kontinuum! Eine Lösung, die rechts eine Welle enthält, ist formal
auch möglich, führt aber zu einem physikalisch inakzeptablen Wert R > 1 des Reflexionskoeffizienten). Dieses Verhalten wurde zuerst von Klein gefunden und ist unter dem Namen
Klein’sches Paradoxon bekannt.
4.4
Die Löchertheorie
Bisher haben wir drei physikalisch schwerverdauliche Konsequenzen aus der Diractheorie
gefunden:
1: Die Instabilität der Zustände mit E > 0 gegenüber strahlendem Zerfall in Zustände
des unteren Kontinuums
2: Das Instabilwerden von gebundenen Zuständen beim Eintauchen in das untere Kontinuum
3: Das Klein’sche Paradoxon
Zur Beseitigung dieser Mängel stellte Dirac die Hypothese auf, dass sämtliche Zustände
mit E < −mc2 (für den feldfreien Raum) besetzt sind, mit vielleicht sehr wenigen Ausnahmen. Ein fehlendes Elektron in einem Zustand negativer Energie verhält sich wie ein
positiv geladenes Teilchen mit Energie, Impuls und Spin entgegengesetzt zu demjenigen des
fehlenden Elektrons. Dieses Loch hat dieselbe Masse wie das Elektron; es wird Positron
KAPITEL 4. DIE DIRAC-GLEICHUNG
106
genannt und wurde kurz nach dem Vorschlag von Dirac auch experimentell von Anderson
in der kosmischen Strahlung gefunden. Positronen können dadurch erzeugt werden, dass
ein γ-Quant ein Elektron aus einem Zustand mit E < 0 in einen mit E > 0 anhebt. In der
neuen Sprachregelung heißt dies: Das Photon erzeugt ein Elektron-Positron-Paar.
Der Einwand der Instabilität von Atomen und freien Elektronen ist durch die Dirachypothese beseitigt. (Dies zeigt übrigens, dass die Diracgleichung nur für Fermionen eine
akzeptable Beschreibung darstellt.) Beim Eintauchen eines unbesetzten gebundenen Zustands in das Kontinuum wird er ”sofort” von einem Elektron aus dem ”Dirac-Meer” besetzt.
Experimentell würde dies bedeuten, dass bei der Bildung eines ”überkritischen” Potentials
(z.B. beim Zusammenstoß zweier hochgeladener Kerne) eine beachtliche Zahl von ungepaarten Positronen emittiert wird, was auch wieder der Beobachtung entspricht. Auf eine
detaillierte Deutung des Klein’schen Paradoxons in der Löchertheorie werden wir verzichten, weil die dort vorausgesetzte Situation (zwei unendliche Halbräume mit unterschiedlichem Potential) unphysikalisch ist und höchstens als Grenzfall eines Kastenpotentials mit
großer Breite von Bedeutung sein kann. Die in einem solchen Gebiet über die Schwelle
E = mc2 hinausgehobenen besetzten Zustände entleeren sich (Bildung lokalisierter Positronen unter Emission freier Elektronen) und die so gebildete Raumladung bringt dann
das überkritische Potential bis auf den Wert 2mc2 hinunter.
Anwendung: Streuung von Licht an freien Elektronen
Die Wechselwirkung eines Diracteilchens mit einem Strahlungsfeld kann analog zur Theorie
in Kap. 2 aufgezogen werden, indem man A(r, t) in der Diracgleichung durch den Operator
für das quantisierte Strahlungsfeld ersetzt. Wir werden als Beispiel für das Funktionieren
der Löcherhypothese die Streuung von Licht an freien Elektronen studieren. Die klassische
Theorie liefert hier den Streuquerschnitt
dσ
= r02 |êi · êj |2
dΩ
2
e
wobei r0 = mc
2 der klassische Elektronenradius ist und êi bzw. êj die Polarisationsvektoren
des einfallenden bzw. gestreuten Photons. (Dieses Ergebnis folgt aus der Formel auf S. 30,
wenn man bedenkt, dass der Operator p keine Übergänge zwischen verschiedenen Zuständen eines freien Elektrons vermitteln kann; dann gilt auch ωk = ωk0 .) Der verbleibende
Term im Ausdruck auf S. 30 kommt vom A2 -Term in der klassischen Wechselwirkung, der
in der Diractheorie kein direktes Analogon hat. Die Wechselwirkung in der Diractheorie ist
gegeben durch
HI = −e~
αA(r, t).
Für die Streuamplitude bis zur zweiten Ordnung gemäß dem zweiten und dritten Graphen
auf S. 30:
107
KAPITEL 4. DIE DIRAC-GLEICHUNG
p' r'
p' r'
k' j
k' j
p'' r''
+
pr
p'' r''
ki
pr
ki
erhält man in Analogie mit der unteren Formel auf S. 31:
0 0
0
p r |~
α · êj e−ik r |p00 r00 p00 r00 |~
α · êi eikr |pr
−2πe2 c2 ~ X X
√
V ωk ωk0 p00 r00 =1,2
E” − E − ~ωk
!
0 0
0
α · êj e−ik r |pr
p r |~
α · êi eikr |p00 r00 p00 r00 |~
+
.
E” − E + ~ωk0
Für p = 0 tragen nur die Zwischenzustände p00 = ~k bzw. p00 = −~k0 bei. Weil α
~ nur zwischen großen und kleinen Komponenten der Eigenspinoren nichtverschwindende Matrixelemente hat, erhält man für das Verhältnis des obigen Ausdrucks zum nichtrelativistischen
Ausdruck auf S. 36
#
"
2
~ωk
1
mc2 X
c~k
2
=O
...
= O mc
.
(êi · êj ) r00
mc2
~ck
mc2
Dieser Ausdruck verschwindet für ωk → 0! Es gibt in der Diractheorie aber noch eine
dritte Möglichkeit: Das einkommende Photon kann ein Elektron-Positron Paar erzeugen;
das Positron vernichtet dann das ursprünglich anwesende Elektron unter Emission eines
Photons. Diese und eine vierte Möglichkeit sind in den unten skizzierten Diagrammen
angegeben:
k' j
k' j
p'' r''
p' r'
p'' r''
+
pr
pr
ki
ki
p' r'
108
KAPITEL 4. DIE DIRAC-GLEICHUNG
Die zugehörige Amplitude ist
00 00
0
p r |~
α · êj e−ik r |pr p0 r0 |~
α · êi eikr |p00 r00
−2πe2 c2 ~ X X
√
V ωk ωk0 p00 r00 =3,4
E’ + |E”| − ~ωk
00 00
!
0
p r |~
α · êi eikr |pr p0 r0 |~
α · êj e−ik r |p00 r00
+
.
E’ + |E”| + ~ωk0
Für p = 0 und ~ωk mc2 gilt in guter Näherung
u(r) (p0 ) ≈ u(r) (p00 ) ≈ u(r) (0)
0
eikr ≈ e−ik r ≈ 1
und
E’ + |E”| − ~ωk ≈ E’ + |E”| + ~ωk0 ≈ 2mc2 .
Falls man weiters noch schreibt
(r) χ+
(r)
u (0) =
für r = 1, 2
0
(r)
u (0) =
0
(r)
χ−
für r = 3, 4 ,
so erhält man für die obige Summe
0
00
0
1 X (r00 )†
(r)
(r )†
(r00 )
(r )†
(r)
(r )†
(r00 )
χ
~σ · êj χ+
χ+ ~σ · êi χ−
+ χ− ~σ · êi χ+
χ+ ~σ · êj χ−
,
2mc2 r00 =3,4 −
(r)
was sich wegen der Vollständigkeit der χ− schreiben lässt als
1
1
(r0 )†
(r)
χ+ [~σ êj ~σ êi + ~σ êi ~σ êj ] χ+ =
êi êj δrr0 ,
2
2mc
mc2
also genau das zur Erhaltung des klassischen Resultats benötigte Ergebnis.
Das obige Ergebnis zeigt auf recht beeindruckende Weise, dass die Diractheorie erst mit
Berücksichtigung der Zustände negativer Energie und der Löcherhypothese zu Übereinstimmung mit den bekannten experimentellen Ergebnissen führt. In den obigen Diagrammen
wurde gemäß einer von Feynman vorgeschlagenen Konvention das Positron als ein sich
rückwärts in der Zeit bewegendes Elektron gezeichnet. Der in den Diagrammen auftretende Zwischenzustand ist weiters für nichtrelativistische Ausgangsteilchen mit einem
riesigen Energieexzess behaftet, also extrem kurzlebig. Das könnte man dadurch zum Ausdruck bringen, dass man die beiden Vertizes extrem nahe zusammenzeichnet; damit ist der
Übergang zum nichtrelativistischen A2 -Graphen auch ”anschaulich” plausibel zu machen!
Zum Schluss: Mit der Löcherhypothese hört die Diractheorie auf, eine echte Einteilchentheorie zu sein. Sie ist eigentlich nur als Vielteilchentheorie konsisten interpretierbar, und es
liegt nahe, auch das Diracfeld als Operatorfeld umzudefinieren. In einer solchen Feldtheorie
109
KAPITEL 4. DIE DIRAC-GLEICHUNG
kann man auch einige etwas beunruhigende Aspekte der Löchertheorie (unendliche Massenund Ladungsdichte des Vakuums) durch Renomierung wegdefinieren. Die Quantenelektrodynamik, d.h. die Theorie der gekoppelten quantisierten Dirac- und Maxwellfelder,
ist trotz der in ihr notwendigen, formal sehr abenteuerlichen, Renormierungsverfahren, die
wohl erfolgreichste fundamentale Theorie der heutigen Physik; sie erlaubt z.B. eine sehr
präzise Berechnung der Lambverschiebung und des, in der Vorlesung nicht diskutierten,
anomalen magnetischen Moments von Elektron und Myon. Weiters ist sie das Vorbild
weiterer in der Elementarteilchenphysik benützter Feldtheorien für starke und schwache
Wechselwirkungen. Lehrbücher, die die Quantenelektrodynamik behandeln, sind z.B. Sakurai und Messiah; siehe auch R. P. Feynman, Quantum Elektrodynamics, sowie sein für
Laien verfasstes QED, The Strange Theory of Light and Matter.
4.5
Quantisierung des Diracfeldes
Ganz analog zur Vorgangsweise bei dem Maxwell- bzw. Schrödingerfeld führen wir einen
Feldoperator für das Diracfeld ein mittels der Definition
r
4
mc2 X X 1
p
b(r) (t)u(r) (p) eipr/~
(5.1)
ψ(r, t) =
V p r=1 |E| p
(r)
und interpretieren die bp (t) als Vernichter eines Elektrons im Zustand (p, r). Sie erfüllen
also die Antivertauschungsbeziehungen
n
o
n
o n
o
(s)†
(r) (s)
(r)† (s)†
0
b(r)
,
b
=
δ
δ
;
b
,
b
=
b
,
b
= 0.
rs pp
p
p
p
p0
p0
p0
Der Hamiltonoperator für das freie Diracfeld lautet dann
Z
H = dr H(r)
H(r) = ψ † (r) HD ψ(r)
mit
HD = −i~c α
~ ∇ + βmc2 .
Einsetzen der Entwicklung (5.1) in H liefert
H = ··· =
XXXX
p
p0
r
r0
XX
mc2 E (r)† (r0 ) (r)†
0
(r)
bp bp0 u (p) u(r ) (p0 ) =
ηr |E|b(r)†
δpp0 p
p bp
|EE’|
p
r
mit
η1 = η2 = 1;
η3 = η4 = −1,
E = Ep = ±
p
p2 c2 + m2 c4 .
110
KAPITEL 4. DIE DIRAC-GLEICHUNG
(r)
Mit Hilfe dieses Hamiltonoperators erhalten wir als Bewegungsgleichung für die bp und
(r)†
bp
i
i
d (r)
= −ηr |E| bp(r)
bp =
H, b(r)
p
dt
~
~
d (r)†
i
i
b
=
H, b(r)†
= ηr |E| b(r)†
p
p
dt p
~
~
Die Lösungen dieser Gleichung können verwendet werden, um in (5.1) die Heisenbergope(r)
(r)
(r)
ratoren bp (t) zugunsten der Schrödingeroperatoren bp ≡ bp (0) zu eliminieren:
r
i
mc2 X X 1 (r) (r)
p bp u (p)e ~ (pr−ηr |E|t) .
ψ(r, t) =
V p r
|E|
Neben der Gesamtenergie H benötigen wir später noch Ausdrücke für die Gesamtladung
Z
X
(r)
e b(r)†
Q = e dr ψ † (r)ψ(r) =
p bp
p,r
und für den Gesamtimpuls
Z
X
(r)
P = −i~ dr ψ † (r)∇ψ(r) =
p b(r)†
p bp
p,r
Der Grundzustand (oder Vakuumzustand) des freien Diracfeldes entspricht gemäß
der Löchertheorie dem Zustand, in dem alle ”Orbitale” mit r = 1, 2 leer und alle ”Orbitale”
mit r = 3, 4 besetzt sind:
b(r)
b(r)†
p |vac = 0, r = 1, 2
p |vac = 0, r = 3, 4 .
(r)
Für r = 3, 4 hebt der Operator bp die Energie des Vakuums um E an, und erniedrigt
gleichzeitig den Impuls um p und die Ladung um e. Diese Operatoren verhalten sich also
gewissermaßen als Erzeuger für positiv geladene Teilchen, die Positronen. Wir definieren
die Erzeuger für Positronen mittels:
(4)
d(1)†
= −b−p ;
p
(3)
d(2)†
= b−p
p
Die Korrespondenz 1 ↔ 4, 2 ↔ 3 sorgt dafür, dass für p ≈ 0 die Erzeuger mit Index 1
die z-Komponente des Spins um ~2 erhöhen. Die Vorzeichen sorgen dafür, dass die JordanWigner Phasenkonventionen erhalten bleiben, falls wir das Vakuum neu definieren als den
Zustand, in dem sämtliche Elektron- und Positron-Orbitale leer sind:
b(r)
d(r)
p |vac = 0,
p |vac = 0, r = 1, 2 .
Die Antikommutatoren lauten, wie erwartet,
n
o
(r0 )†
d(r)
,
d
= δrr0 δpp0 ;
0
p
p
111
KAPITEL 4. DIE DIRAC-GLEICHUNG
Antikommutatoren vom Typ {d, d}, d† , d† , sowie {d, b}, d† , b usw. verschwinden alle.
Falls wir weiters Positron-Spinoren einführen mittels:
v (1) (p) = −u(4) (−p)
v (2) (p) = u(3) (−p) ,
so können wir den Feldoperator ψ umschreiben als
r
X X mc2 (s)
i(pr−Et)/~
(s)
−i(pr−Et)/~
b(s)
+ d(s)†
,
ψ(r, t) =
p u (p) e
p v (p) e
E
V
p s=1,2
p
wobei E ab jetzt immer dem positiven Ausdruck E(p) = + p2 c2 + m2 c4 entspricht. Bei der
obigen Umformung haben wir benutzt, dass die Summation in (5.1) sämtliche p umfasst,
sodass p unter der Summation durch −p ersetzt werden kann.
Der Hamiltonperator in den neuen Operatoren lautet
XX
XX
(s) (s)†
(s)
(s)
(s)† (s)
EP b(s)†
b
−
d
d
=
EP b(s)†
H=
−p −p
p
p
p bp + d p d p − 1 ,
p s=1,2
p
s
wobei wir die Antivertauschungsrelation ausgenützt und im zweiten Term den Summationsindex von p in −p umbenannt haben. Der Term −1 im Summanden ist eine (divergente)
Konstante und wird üblicherweise weggelassen. Für die Gesamtladung erhält man analogerweise
X
(s) (s)†
(s)† (s)
bp bp + d−p d−p
Q=e
ps
=e
X
ps
(s)
(s)† (s)
b(s)†
p b p − dp dp + 1
Hier sieht man also explizit, dass die Positronen positive Ladung tragen (e = −|e|). Weiters
tritt hier eine unübliche ”Hintergrundladung des Dirac-Sees” auf; dieser Term wird üblicherweise auch ohne viel Kommentar gestrichen. Allerdings bietet sich in jüngster Zeit eine
attraktive Alternative an: in den erfolgreicheren modernen Theorien der Elementarteilchen
treten diese in ”Generationen” auf. Zu dem Elektron mit Ladung −|e| (und dem ungeladenen Elektronneutrino) gehören in einer Generation zwei Quarks mit Ladung 32 |e| und
− 31 |e|, die auch Spin 12 haben und weiters noch in drei Varianten (Farben)
vorkommen. Die
2
1
Gesamtladung der Orbitale mit Impuls p ist also: 2 −|e| + 3 3 − 3 |e| = 0, und auch
die Hintergrundladungen der Diracseen addieren sich innerhalb der Generation zu Null.
Wechselwirkungen
In einer relativistisch invarianten Theorie ist es unschön, ein Wechselwirkungspotential
V (r1 − r2 ) zwischen zwei Fermionen einzuführen: eine instantane Wechselwirkung zwischen
zwei zueinander raumartig gelegenen Teilchen verträgt sich schlecht mit der relativistischen
Kausalität (nur zueinander raumartig gelegene Ereignisse können einander beeinflussen).
112
KAPITEL 4. DIE DIRAC-GLEICHUNG
Stattdessen lässt man sich inspirieren von der Methode der Ankopplung von geladenen Teilchen an das Maxwellfeld (oder von den Elektronen an den Phononen in der Festkörperphysik). Der Wechselwirkungsterm (in der Hamiltondichte, oder, auf etwas fundamentalerem
Niveau, in der Lagrangedichte) hat die Form
wobei
LI = G J A,
G eine Zahl (Kopplungskonstante) ist,
J ein ”Strom” bilinear in den Fermionenfeldern, und
A ein Kraftfeld (Bosonfeld) ist
(in komplizierteren Theorien treten auch Ströme aus Bosonenfeldern auf).
Weiters soll LI eine skalare Dichte sein; dies heißt, dass J und A unter Lorentztransformationen ähnlich transformieren müssen. Weil das Maxwellfeld Aµ ein Vektorfeld ist, darf
es nur an einen Vektorstrom ankoppeln; wir haben in der Tat gesehen, dass die Stromdichte
Jµ = ψ̄γµ ψ = ψ † αψ, ψ † ψ
wie ein Vektor p, Ec transformiert.
Die schwache Wechselwirkung sollte z.B. imstande sein, Zerfälle wie
µ− −→ e− + ν̄e + νµ
zu beschreiben. Dies geschieht durch Ankopplung an ein intermediäres Vektorboson W± ;
der obige Prozess wird zerlegt in
µ− −→ W− + νµ
W− −→ ν̄e + e−
oder auch (vgl. die Thomsonstreuung)
|0 −→ W+ + e− + ν̄e
µ− + W+ −→ νµ
νµ
µ−
e−
W±
ν̄e
KAPITEL 4. DIE DIRAC-GLEICHUNG
113
Der schwache Strom muss also Terme enthalten, die ein Myon vernichten und ein MyonNeutrino erzeugen (oder ein Elektron und ein Elektron-Antineutrino erzeugen). Ein Ansatz
wäre
?
Jµw = ψ̄νe γµ ψe + ψ̄νµ γµ ψm + h.c.
(5.2)
wobei der Myonspinor mit ψm bezeichnet wurde. Da das W± -Teilchen sehr massiv ist, führt
es in dem skizzierten Prozess zu sehr großen Energienennern, also zu sehr schwacher Wechselwirkungen, sogar falls die Kopplungskonstante mit derjenigen der elektromagnetischen
Wechselwirkung vergleichbar ist. (Allerdings nicht mehr, falls die Energie des einfallenden
Teilchens mit mW c2 vergleichbar ist.)
Der obige Ansatz kann aber nicht richtig sein, weil das Neutrino nur zwei Komponenten
hat; das Neutrino kommt nur als linkshändiges Teilchen vor! Wir müssen im Stromoperator
also auf linkshändige Teilchen projizieren. Für masselose Teilchen hat der Diracspinor die
Form
(+) χ
χ(+)
=
wegen E = c|p|.
σ·pc (+)
χ
σ · p̂ χ(+)
|E|
Wegen [σ · p̂]2 = I gilt also
χ(+)
σ · p̂ 0
χ(+)
σ · p̂ χ(+)
Σ · p̂
=
=
,
0 σ · p̂
σ · p̂ χ(+)
σ · p̂ χ(+)
χ(+)
d.h. Σ · p̂ = −γ5 mit
γ5 = γ1 γ2 γ3 γ4 =
0 −I
.
−I 0
Der Projektor auf die linkshändigen Teilchen hat also die Form 21 (1 + γ5 ). Weiters sieht
man, dass γ5 mit einem Pseudoskalar (Vektorprodukt eines axialen mit einem polaren Vektor) zusammenhängt; dies wird bestätigt durch eine Analyse des Verhaltens der γ-Matrizen
unter Lorentztransformationen, die ergibt, dass γ5 mit eigentlichen Lorentztransformationen kommutiert, aber mit Raumspiegelungen antikommutiert. Durch Überlegungen dieser
Art wird man dazu geführt, statt (5.2) anzusetzen
Jµw = ψ̄νe γµ (1 + γ5 ) ψe + ψ̄νµ γµ (1 + γ5 ) ψm + . . . ,
wobei benützt wurde, dass γ5 mit allen γµ antivertauscht. Aus dieser Form geht hervor, dass
in der schwachen Wechselwirkung, d.h. beim Zerfall des W− -Teilchens, nur linkshändige
Elektronen produziert werden (auch beim Zerfall des Neutrons, wobei das W− durch ein
Nukleon- (oder Quark-)-Anteil in Jµw produziert wurde). Diese Vermutung wurde schon
1958 durch Wu et al. experimentell bestätigt.
In der vereinheitlichten Theorie der elektromagnetischen und schwachen Wechselwirkungen kann zusätzlich zum Photon und zum W± noch ein viertes Teilchen, das Z0 , ausgetauscht werden. Der zugehörige Strom enthält neben einem reinen ψ̄νe γµ (1 + γ5 )ψν Term
114
KAPITEL 4. DIE DIRAC-GLEICHUNG
auch neutrale (ladungserhaltende) Ströme aus geladenen Teilchen (mit irgendeiner Kombination aus γµ und γµ γ5 ). Dieser Term führt zu e − ν-Streuung.
e−
ν
Z0
e−
ν
Durch Drehung dieses Diagramms sieht man, dass das Z0 durch e+ − e− Vernichtung erzeugt werden kann, und dann in alle möglichen Teilchen-Antiteilchen Paare zerfallen kann.
Aus der Lebensdauer des Z0 -Teilchens kann man dementsprechend die gesamte Zahl der
Elementarteilchen (mit Masse kleiner als 12 MZ0 ) bestimmen. Die im letzten Jahr angelaufenen Experimente zeigen, dass es neben den bisher bekannten Teilchen keine weiteren zu
geben scheint, also insbesondere keine weiteren masselosen Neutrinos (neben νe , νµ und
ντ ).