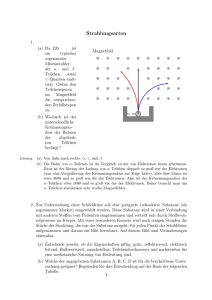
Zusatzmaterial 2 3.3 Massen und Stoffmengen Stöchiometrie: Sie

1
Zusatzmaterial 2
3.3 Massen und Stoffmengen
Stöchiometrie:
Sie befaßt sich mit Mengenverhältnissen der Elemente in Verbindungen und mit
quantitativen Beziehungen von Elementen oder Verbindungen, die an chemischen
Reaktionen beteiligt sind.
Typische Fragestellungen:
1. Berechnung von molaren Molekülmassen / Formelmassen
Beispiel Methan: CH4:
M(CH4) = M(C) + 4 . M(H) = (12,011 + 4 . 1,008) g/mol = 16,043 g/mol
2. Berechnung der prozentualen Zusammensetzung
a) Massenanteile (Massenprozente) oder b) Mengenanteile (Atomprozente)
3. Aufstellen von Reaktionsgleichungen
4. Ermittlung einer Formel aus Analysendaten
4 Das Periodensystem der Elemente (PSE)
4.1 Historisches
! Arbeiten von 1869 von Lothar Meyer (1830 – 1895) und Dmitri Mendelejew
(1834 – 1907): Systematische Anordnung der Elemente nach zunehmender
Atommasse, wodurch Eigenschaften der Elemente periodisch auftauchten.
! Erst 60 Elemente waren bekannt.
! Mendelejew hat Eigenschaften von unbekannten Elementen richtig vorhergesagt
(Scandium, Gallium, Germanium).
! Probleme bei: Argon – Kalium
Cobalt – Nickel
Tellur – Iod
Bei allen drei Paaren mußte aufgrund der chemischen Eigenschaften das schwerere
Element vor dem leichteren einsortiert werden!
⇒
Das Ordnungsprinzip im PSE kann nicht die Masse sein!
2
4.2 Die Elektronenstruktur der Atome
Quantenmechanische Beschreibung
Historisches
1905: Planck und Einstein: E = hν
Licht besteht aus Teilchen, den Photonen.
Welle-Teilchen-Dualismus: Je nach der Art des Experiments kann man Elektronen
einmal besser als Wellen oder besser als Teilchen beschreiben. Elektronen sind
nicht mal Welle mal Teilchen, wir beschreiben sie nur so!
1924: de Broglie:
h
p
Wellenlänge ist gleich der Planck-Konstante geteilt durch den Impuls.
Jedes Objekt hat auch Wellencharakter.
λ =
1926: Heisenbergsche Unschärferelation:
Ort und Geschwindigkeit eines Teilchens sind nicht gleichzeitig genau bestimmbar.
1926: Schrödinger beschreibt die Elektronen als Wellen in Atomen. Die SchrödingerGleichung besitzt heute fundamentale Bedeutung für die Naturwissenschaften.
Ergebnisse der quantenmechanischen Betrachtung
Man unterscheidet die folgenden Quantenzahlen:
1. Hauptquantenzahl n:
n = 1, 2, 3...
(K-, L-, M-...Schale)
Größe
2. Nebenquantenzahl l:
l = 0, 1, 2, ... n – 1
s-, p-, d-, f-Orbital
Form
3. Magnetquantenzahl ml:
ml = -l, -(l – 1), ... +l
2l + 1 Zustände
Orientierung
Die durch die 3 QZ festgelegten Zustände (Wellenfunktion Ψn, l, ml) nennt man
Atomorbitale.
4. Spinquantenzahl ms:
Drehsinn
ms = +1/2 oder –1/2