¨Ubungsblatt 1 zur Teilchenphysik I

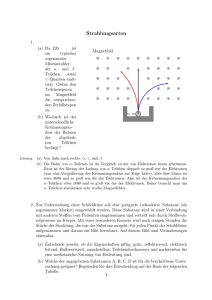
Übungsblatt 1 zur Teilchenphysik I
1) Benutzen Sie die Webpage der Particle Data Group oder andere Informationsquellen, um
folgende Größen im natürlichen Einheitensystem der ETP (h̄ = c = 1) auszudrücken: Atomradius (1 Å), Nukleonradius (1 f m = typische Größe von Atomkernen), klassischer Elektronradius,
Comptonwellenlänge des Elektrons, Gravitationsbeschleunigung auf der Erdoberfläche.
2) Bestimmen Sie wie bei Aufgabe 1 in natürlichen Einheiten die inversen Lebensdauern (auch
genannt Zerfallsbreite Γ = τ −1 ) von Neutron, Myon, den Pionen und dem Rho-Meson (ρ). Vergleichen Sie die Ergebnisse mit den Massen dieser Teilchen. Kann man aus diesen Zahlen etwas
lernen?
3) Schätzen Sie die Masse mY des von Yukawa hypothetisierten Mesons mit der Annahme ab, dass
das Meson ein Potential der Form V (r) ∝ 1r e−rmY besitzt und dass die Reichweite des Potentials
von der Größenordnung des Nukleonradiuses ist.
4) Schätzen Sie die Masse mY ganz anders ab, indem Sie annehmen, dass der Austausch der
Mesonen zwischen den Nukleonen eine Energieunschärfe der Nukleonen von der Größenordung der
Mesonmasse verursacht und dass die entsprechende Ortsunschärfe (maximal) von der Größenordnung
des Kernradiuses ist. Diskutieren Sie Aufgabe 3 und 4.
5) Stellt man ein homogenes und zeitunabhängiges Magnetfeld senkrecht zur Flugrichtung eines
geladenen Teilchens auf und dazu auch ein homogenes und zeitunabhängiges elektrisches Feld
senkrecht zur Laufrichtung des Teilchens und zur Magnetfeldrichtung, dann ist es möglich, dass das
Teilchen ohne Ablenkung fliegt. Welche Geschwindigkeit muss das Teilchen bei gegebenen E- und
B-Feldern dazu haben? Sie schalten nun das E-Feld aus und beobachten dass das Teilchen entlang
einer Kreisbahn mit Radius r fliegt. Bestimmen Sie das Verhältnis von Ladung zu Masse (q/m).
6) Vor der Entdeckung des Neutrons gab es die Vorstellung, dass Atomkerne aus Protonen und Elektronen bestehen, wobei die Atomzahl Z gleich der (im Vergleich zu den Elektronen) überzähligen
Protonen ist. Diese Idee scheint den Beobachtungen zum β-Zerfall nicht zu widersprechen. Trotzdem gibt es hier ein Problem, das diese Idee nicht sehr attraktiv erscheinen lässt. Bestimmen Sie
mit Hilfe der Unschärferelation für Ort und Impuls den minimalen Impuls von Elektronen im Atomkern. Ist das Elektron nicht-relativistisch? (Evtl. müssen Sie hier in ein Buch mit relativistischen
Formeln schauen.) Bestimmen Sie nun die entsprechende typische Energie des Elektronen die beim
β-Zerfall abgestrahlt werden unter der Annahme, dass diese ungefähr der Energie der Elektronen
vor dem Zerfall entspricht. Vergleichen Sie das Ergebnis mit dem Elektronspektrum des β-Zerfalls,
das in der Vorlesung diskutiert wurde.
7) Gruppendiskussion: Welche Schlussfolgerung würden Sie in Bezug auf Aufgabe 6 ziehen? Finden
Sie Argumente als Befürworter und als Gegner der in Aufgabe 6 dargestellten Idee über die Struktur
der Atomkerne.
8) In der Vorlesung wurde erwähnt, dass man sich die Wechselwirkung mittels eines elektromagnetischen Feldes als den Austausch von unendlich vielen Photonen vorstellen sollte. Mit folgender
1
Rechnung lässt sich besser veranschaulichen, was damit gemeint ist.
Bestimmen Sie die Greensfunktion G für die Schrödinger-Gleichung mit dem Hamiltonoperator
H = H 0 + V , wobei H 0 der Hamiltonoperator für die freie Bewegung ist und V der für ein
Potential. Dies Aufgabe kann man ohne großen Aufwand ganz allgemein auf dem Operator-Nivau
ausführen, ohne irgendetwas konkret zu spezifizieren. Konkret können Sie sich das Wasserstoff als
Problem vorstellen. Die Greenfunktion erfüllt also die Gleichung
(H 0 + V ) G = 1 ,
wobei 1 der Einheitsoperator ist. Lösen die Gleichung iterativ, wobei Sie V störungstheoretisch
behandeln, d.h. V H 0 , und zeigen Sie, dass die Lösung die Form
G = G0 − G0 V G0 + G0 V G0 V G0 − . . .
hat. Hierbei ist G0 die freie Greensfunktion (d.h. H 0 G0 = 1). (Bemerkung: Sie können diese
unendliche Summe leicht explizit ausführen.) Die Wirkung von V entspricht dem Effekt vom
Austausch eines (!) Photons. Wie genau sollte man dann den Effekt eines klassischen elektromagnetischen Feldes im Bezug auf den Austausch von Photonen interpretieren?
2