Teil2 - oth-regensburg.de

Algorithmen und Datenstrukturen
2. Datenstrukturen und Algorithmen in C++ und
Java
Datenstrukturen und Algorithmen sind eng miteinander verbunden. Die Wahl der
richtigen Datenstruktur entscheidet über effiziente Laufzeiten. Beide erfüllen nur
alleine ihren Zweck. Leider ist die Wahl der richtigen Datenstruktur nicht so einfach.
Eine Reihe von schwierigen Problenem in der Informatik wurden deshalb noch nicht
gelöst, da eine passende Datenorganisation bis heute noch nicht gefunden wurde.
Wichtige Datenstrukturen (Behälterklassen, Collection, Container) werden in C++
und Java bereitgestellt. Auch Algorithmen befinden sich in diesen "Sammlungen".
Sammlungen (Kollektionen) sind geeignete Datenstrukturen (Behälter) zum
Aufbewahren von Daten. Durch ihre vielfältigen Ausprägungen können sie zur
Lösung unterschiedlicher Aufgaben herangezogen werden. Ein Lösungsweg umfaßt
dann das Erzeugen eines solchen Behälters, das Einfügen, Modifizieren und
Löschen der Datenelemente. Natürlich steht dabei im Mittelpunkt der Zugriff auf die
Datenelemente, das Lesen der Dateninformationen und die aus diesen
Informationen resultierenden Schlußfolgerungen. Verallgemeinert bedeutet dies:
Das Suchen nach bestimmten Datenwerten, die in den Datenelementen der
Datensammlung (Kollektion) gespeichert sind.
Suchmethoden bestehen aus einer Reihe bestimmter Operationen. Im wesentlichen
sind dies
− Das Initialisieren der Kollektion ( die Bildung einer Instanz mit der Datenstruktur, auf der die Suche
erfolgen soll
− das Suchen eines Datenelements (z.B. eines Datensatzes oder mehrerer Datensätze)in der
Datensammlung mit einem gegebenen Kriterium (z.B. einem identifizierenden Schlüssel)
− das Einfügen eines neuen Datenelements. Bevor eingefügt werden kann, muß festgestellt werden,
ob das einzufügende Element in der Kollektion schon vorliegt.
− das Löschen eines Datenelements. Ein Datenelement kann nur dann gelöscht werden, falls das
Element in der Kollektion vorliegt.
Häufig werden Suchvorgänge in bestimmten Kollektionen (Tabellen) benötigt, die
Daten über identifizierende Kriterien (Schlüssel) verwalten. Solche Tabellen können
als Wörterbücher (dictionary) oder Symboltabellen implementiert sein. In einem
Wörterbuch sind bspw. die "Schlüssel" Wörter der deutschen Sprache und die
Datensätze, die zu den Wörtern gehörenden Erläuterungen über Definition,
Aussprache usw. Eine Symboltabelle beschreibt die in einem Programm
verwendeten Wörter (symbolische Namen). Die Datensätze sind die Deklarationen
bzw. Anweisungen des Programms. Für solche Anwendungen sind nur zwei weitere
zusätzliche Operationen interessant:
− Verbinden (Zusammenfügen) von Kollektionen, z.B. von zwei Wörterbüchern zu einem großen
Wörterbuch
− Sortieren von Sammlungen, z.B. des Wörterbuchs nach dem Schlüssel
Die Wahl einer geeigneten Datenstruktur (Behälterklasse) ist der erste Schritt. Im
zweiten Schritt müssen die Algorithmen implementiert werden. Die Standard−
Bibliotheken der Programmiersprachen C++ und Java bieten Standardalgorithmen
an.
1
Algorithmen und Datenstrukturen
2.1 Datenstrukturen und Algorithmen in C++
2.1.1 Die C++−Standardbibliothek und die STL
Der Entwurf der Standard−C++−Bibliothek wurde relativ spät um einen Teil erweitert,
der Standard Template Librarary (STL) genannt wurde, da er u.a. viele Templates
zur Verfügung stellt. Die STL erhöht die Einsetzbarkeit von C++ enorm, da
wesentliche, immer wiederkehrende Templates dort festgelegt sind.
Die wesentlichen Komponenten der STL sind
− Algorithmen
z.B. Sortieren
− Container
, wie bspw. Listen oder Mengen
− Iteratoren
, mit deren Hilfe Container traversiert werden können
− Funktionsobjekte
, die eine Funktion einkapseln, die von anderen Komponenten benutzt werden
kann.
−Adaptoren
durch die eine andere Schnittstelle von einer Komponente gebildet werden kann.
2.1.2 Container
2.1.2.1 Grundlagen
Ein Container ist ein Objekt, das der Speicherung anderer Objekte dient, z.B. eine
Liste, ein Array oder eine Schlange. Mit der Containert−Klasse wird der Typ eines
solchen Objekts definiert. Objekte, die ein Containert speichert, sind die Elemente.
Der Typ der Elemente ist der Elementtyp.
Da Container−Klassen für einen beliebigen Elementtyp definiert werden sollen, sind
in der Standard−C++−Bibliothek Templates für Container−Klassen definiert. Es wird
unterschieden zwischen
− Sequenzen, in denen jedes Element eine Position besitzt, wie z.B. Listen
− Adaptoren für Sequenzen, die einer Sequenz eine andere Schnittstelle verleihen, wie z.B. ein Stapel
− assoziative Container, die jeweils eine Menge von Elementen verwalten, auf die über ihren Inhalt
(Wert) zugegriffen wird (z.B. set und map).
Sequenzen
Adaptoren von Sequenzen
1
Template für Container−Klasse
template <class T1> class vector
template <class T> class list
template <class T> class deque
template <class T,classContainer=deque<T> > class stack
template <class T, class Container = deque<T> > class queue
template <class T,class Container=deque<T>,class Compare=
less<typname Container::value_type> > class priority_queue
T ist jeweils der Elementtyp
2
Algorithmen und Datenstrukturen
Assoziative Container
template <class Key2,class Compare3=less<Key> > class set
template <class Key,class T,class Compare = less<Key> >class map
Abb.: Templates von Container−Klassen
Die Stärke der STL ist, dass, soweit möglich, alle Container die gleiche Schnittstelle
besitzen. Die Schnittstelle wird (leider) nicht in einer abstrakten Klasse definiert
sondern durch eine Tabelle, in der die gemeinsamen Eigenschaften aller Container
festgelegt werden.
Konstruktoren
Destruktoren
Zuweisung
Traversieren
Vergleiche
Größe
Typen
X u;
X()
X(a)
u wird leerer Container
Leerer Container
Neuer Container mit X(a) == a wird erzeugt
X X u; u = a;
u=a
(&a)−>~X()
r=a
a.begin()
a.end()
a == b
a != b
a<b
a>b
a <= b
a >= b
a,size()
a.empty()
X::value_type
X::iterator
X::const_iterator
X::size_type
Der Inhalt des Containers a wird gelöscht
Dem Container mit Referenz r wird er Container a zugewiesen
liefert einen Iterator auf das erste Element des Containers zurück
liefert einen Iterator auf den gedachten Nachfolger des letzten
Elements des Containers a zurück
Prüfen, ob die Container a und b elementweise gleich sind
!(a == b)
Anzahl der Elemente in a
a.size() == 0
Elementtyp
Typ eines Iterators, der auf ein Element zeigt
Typ eines Iterators, der auf ein konstantes Element zeigt
Typ nicht negativer Werte von bspw. Iteratordifferenzen und von
size()
Abb.: Wichtige Eigenschaften eines Containers
2.1.2.2 STL−Container−Anwendungen
1. "priority_queue" container adaptor
neue Einträge
Eintrag
Eintrag
Eintrag
Eintrag
Eintrag
pop()
push()
niedrigste
...........
dritthöchste zweithöchste höchste
Priorität
Abb.: Eine Priority Queue
Die "priority_queue" nutzt die "Container"−Klassen "vector"
deque.Typische Deklarationen zu einer "priority_queue" sind:
2
3
Key ist der Typ der Schlüssel der abgespeicherten Elemente
Compare ist eine Vergleichsklasse
3
bzw.
Algorithmen und Datenstrukturen
priority_queue< vector<node> > x;
priority_queue< deque<string>,case_insensitive_compare > y;
priority_queue< vector<int>, greater<int> > z;
Die Implementierung der "priority−queue" in der STL−Version von Hewlett
Packard zeigt folgende Aussehen:
template <class Container, class Compare> class priority_queue
{
protected :
Container c;
Compare comp;
?
public :
bool empty() const { return c.empty(); }
size_type size() const { return c.size() }
value_type& top() const { return c.front(); }
void push(const value_type& x
{
c.push_back(x);
push_heap(c.begin(), c.end(), comp);
}
void pop()
{
pop_heap(c.begin(), c.end(), comp);
c.pop_back();
}
}
Die STL−Funktionen push_heap() und pop_heap() werden zur Implementierung
herangezogen. push() fügt das neue Element an das Ende des Container,
push_heap() bringt danach das Element an seinen richtigen Platz. pop() ruft
zuerst pop_heap() auf. pop_heap() bringt das Element an das Ende des
Container, pop_back() entfernt das Element und verkürzt den Container.
Man kann aus dieser Anwendung ersehen, wie leicht es wurde, eine Container−
Klasse mit Hilfe der STL einzurichten.
Die "priority_queue" der STL ist ein Adapter und stützt sich ab auf die Klassen
vector bzw. deque. Präsentiert wird ein Interface, das zusätzlich zu den üblichen
Container−Methoden fünf Member−Funktionen bereitstellt.
2. Huffman Coding mit "priority_queue"−Container
4
Gegeben ist eine Datei, z.B. mit folgendem Inhalt
AAAAAAAAAAAAAA
BBB
C
D
E
F
GGG
HHHH
Gesucht ist eine geeignete Binärcodierung (Code variabler Länge), die die Häufigkeit
des Auftretens der Zeichen berücksichtigt.
Der Huffman−Algorithmus relisiert die Binärcodierung mit Hilfe eines Binärbaums,
der folgendes Aussehen haben könnte:
4
vgl. 3.1.2.2
4
Algorithmen und Datenstrukturen
28
0
1
14
14
0
1
A
6
8
0
1
0
3
3
4
1
4
0
B
G
1
H
2
0
2
1
0
1
1
1
1
C
F
D
1
Abb.: Huffman−Codierungs−Baum
E
Jeder Knoten hat ein Gewicht, der den Platz im Huffman−Codierungs−Baum
festlegt. Die STL "priority_queue" wird zunächst zur Aufnahme der eingelesenen
Zeichen benutzt. Je nach Häufigkeit des Vorkommens der Zeichen erfolgt die
Einordnung.
Danach werden die beiden Einträge (Knoten) mit der niedrigsten Priorität entfernt,
ein neuer interner Knoten (Addition der Gewichte) gebildet. Der neue Knoten wird
wiedern in die priority_queue gebracht. Das wird solange wiederholt bis nur ein
einziger Knoten in der priority_queue vorliegt.
5
Algorithmen und Datenstrukturen
2.1.3 Iteratoren
Bei allen Containern werden Iteratoren verwendet, um einen Container zu
traversieren oder evtl. auch, um auf ein bestimmtes Element zu verweisen. Die
einzelnen Container stellen bidirektionale Iteratoren oder Iteratoren zum wahlfreiem
Zugriff bereit.
vector<T>::iterator
list<T>::iterator
deque<T>::iterator
set<T,Compare>::iterator
multiset<T,Compare>::iterator5
map<Key,T,Compare6>::iterator
multimap<Key,T,Compare>::iterator
random_access_iterator
bidirectional−iterator
random_access_iterator
bidirectional_iterator
bidirectional_iterator
bidirectional_iterator
bidirectional_iterator
− Iteratoren sind Verallgemeinerungen von Zeigern
− Zeiger sind Iteratoren im Sinne der STL und können überall eingesetzt werden, wo
Iteratoren benutzt werden
− Vorwärtsiteratoren unterstützen Prä− und Postinkrement (++).
− Rückwärtsiteratoren unterstützen Prä− und Postdekrement (−−). Nicht alle
Container bieten Rückwärtsiteratoren
− Random−Access−Iteratoren unterstützen Zeiger−Arithmetik
− Die Algorithmen der STL operieren auf Iteratoren.
2.1.4 Algorithmen
Algorithmen operieren auf Containern oder Iteratoren. Ihr Verhalten kann über
Template−Argumente gesteuert werden.
5
6
Iteratoren des Typs map bzw. multimap liefern Werte des Typs pair<Key,Value>
Compare definiert eine Ordnungsfunktion auf Key
6
Algorithmen und Datenstrukturen
2.2 Datenstrukturen und Algorithmen in Java
2.2.1 Durchwandern von Daten mit Iteratoren
Bei Datenstrukturen gibt es eine Möglichkeit, gespeicherte Daten unabhängig von
der Implementierung immer mit der gleichen Technik abzufragen. Bei
Datenstrukturen handelt es sich meistens um Daten in Listen, Bäumen oder
ähnlichem und oft wird nur die Frage nach der Zugehörigkeit eines Worts zum
Datenbestand gestellt (z.B. "Gehört das Wort dazu?"). Auch die Möglichkeit Daten in
irgendeiner Form aufzuzählen, ist eine häufig gestellte Aufgabe. Hierfür bieten sich
Iteratoren an. In Java umfaßt das Interface Enumeration die beiden Funktionen
hasMoreElements() und nextElement(), mit denen durch eine Datenstruktur
iteriert werden kann.
public interface Enumeration
{
public boolean hasMoreElements();
// Test, ob noch ein weiteres Element aufgezählt werden kann
public Object nextElement() throws NoSuchElementException;
/* setzt den internen Zeiger auf das nächste Element, d. h. liefert das
das nächste Element der Enumertion zurück. Diese Funktion kann eine
NoSuchException auslösen, wenn nextElement() aufgerufen wird, obwohl
hasMoreElements() unwahr ist
*/
}
Die Aufzählung erfolgt meistens über
for (Enumeration e = ds.elements(); e.hasMoreElements(); )
System.out.println(e.nextElements());
Die Datenstruktur ds besitzt eine Methode elements(), die ein Enumeration−
Objekt zurückgibt, das die Aufzählung erlaubt.
2.2.2 Die Klasse Vector
class java.util.Vector extends AbstractList
implements List, Cloneable,
Serializable
Die Klasse Vector beschreibt ein Array mit variabler Länge. Objekte der Klasse
Vector sind Repräsentationen einer linearen Liste. Die Liste kann Elemente
beliebigen Typs enthalten, ihre Länge ist zur Laufzeit veränderbar (Array mit
variabler Länge). Vector erlaubt das Einfügen von Elementen an beliebiger Stelle,
bietet sequentiellen und wahlfreien Zugriff auf die Elemente. Das JDK realisiert
Vector als Array von Elementen des Typs Object. Der Zugriff auf Elemente erfolgt
über Indizes. Es wird dazu aber kein Operator [], sondern es werden Methoden
benutzt, die einen Index als Parameter annehmen.
Anlegen eines neuen Vektors (Konstruktor): public Vector()
public Vector(int initialCapacity,int capacityIncrement)
// Ein Vector vergrößert sich automatisch, falls mehr Elemente aufgenommen werden, als
// ursprünglich vorgesehen (Resizing). Dabei sollen initialCapacity und capacityIncrement
// passend gewählt werden.
7
Algorithmen und Datenstrukturen
Einfügen von Elementen: public void addElement(Object obj)
// Anhängen an des Ende der bisher vorliegenden Liste von Elementen
Eigenschaften: public final boolean isEmpty()
// Prüfen, ob der Vektor leer ist
public final int size()
// bestimmt die Anzahl der Elemente
public final int capacity()
// bestimmt die interne Größe des Arrays. Sie kann mit ensureCapacity() geändert
// werden
Einfügen an beliebiger Stelle innerhalb der Liste:
public void insertElementAt(Object obj, int index) throws
ArrayIndexOutOfBoundsException
// fügt obj an die Position index in den "Vector" ein.
Zugriff auf Elemente: Für den sequentiellen Zugriff steht ein Iterator zur Verfügung.
Wahlfreier Zugriff erfolgt über:
public Object firstElement() throws ArrayIndexOutOfBoundException;
public Object lastElement() throws ArrayIndexOutOfBoundException;
public Object elementAt(int index) throws ArrayIndexOutOfBoundException;
firstElement() liefert das erste, lastElement() das letzte Element− Mit
elementAt() wird auf das Element an der Position index zugegriffen. Alle 3
Methoden verursachen eine Ausnahme, wenn das gewünschte Element nicht
vorhanden ist.
Arbeitsweise des internen Arrays. Der Vector vergrößert sich automatisch, falls mehr
Elemente aufgenommen werden. Die Operation heißt Resizing.
Die Größe des Felds. Mit capacity() erhält man die interne Größe des Arrays. Sie
kann mit ensureCapacity() geändert werden. ensureCapacity(int
minimumCapacity) bewirkt bei einem Vector, daß er mindestens minCapacity
Elemente aufnehmen soll.
Der Vektor verkleinert nicht die aktuelle Kapazität, falls sie schon höher als
minCapacity ist. Zur Veränderung dieser Größe, dient die Methode trimToSize().
Sie reduziert die Kapazität des Vectors auf die Anzahl der Elemente, die gerade im
Vector sind.
Die Anzahl der Elemente kann über die Methode size() erfragt werden. Sie kann
über setSize(int newSize) geändert werden. Ist die neue Größe kleiner als die
alte, so werden die Elemente am Ende des Vectors abgeschnitten. Ist newSize
größer als die alte Größe, werden die neu angelegten Elemente mit null initialisiert.
Bereitstellen des Interface Enumerartion. In der Klasse Vector liefert die Methode
public Enumeration elements() einen Enumerator (Iterator) für alle
Elemente, die sich in Vector befinden.
8
Algorithmen und Datenstrukturen
Vector
<< Konstruktoren >>
public Vector()
// Ein Vector in der Anfangsgröße von 10 Elementen wird angelegt
public Vector(int startKapazitaet)
// Ein Vector enthält Platz für startKapazitaet Elemente
public Vector(int startKapazitaet, int kapazitaetsSchrittweite)
<< Methoden >>
public final synchronized Object elementAt(int index)
// Das an der Stelle index befindliche Objekt wird zurückgegeben
public final int size()
public final synchronized Object firstElement()
public final synchronized Object lastElement();
public final synchronized void insertElementAt(Object obj, int index)
// fügt Object obj an index ein und verschiebt die anderen Elemente
public final synchronized void setElementAt(Object obj, int index)
public final synchronized copyInto(Object einArray[])
// kopiert die Elemente des Vektors in das Array einArray
// Falls das bereitgestellte Objektfeld nicht so groß ist wie der Vektor,
// dann tritt eine ArrayIndexOutOfBounds Exception
public final boolean contains(Object obj)
// sucht das Element, liefert true zurück wenn o im Vector vorkommt
public final int indexOf(Object obj)
// sucht im Vector nach dem Objekt obj. Falls obj nicht in der Liste ist, wird
// −1 übergeben
public final int lastIndexOf(Object obj)
public final synchronized boolean removeElement(Object obj)
// entfernt obj aus der Liste. Konnte es entfernt werden, wird true
// zurückgeliefert
public final synchronized void removeElementAt(int index)
// entfernt das Element an Stelle index
public final synchronized void removeAllElements()
// löscht alle Elemente
public final int capacity()
// gibt an, wieviel Elemente im Vektor Patz haben
// (, ohne daßautomatische Größenanpassung erfolgt)
public synchronized Object clone()
// Implementierung der clone()−methode von Object, d.h. eine Referenz
// das kopierte Feld wird zurückgegeben. Die Kopie ist flach.
public final synchronized String toString()
Abb.: Die Klasse Vector
9
Algorithmen und Datenstrukturen
2.2.3 Die Klasse Stack
class java.util.Stack extends Vector
Ein Stack ist eine nach dem LIFO−Prinzip arbeitende Datenstruktur. Elemente
werden vorn (am vorderen Ende der Liste) eingefügt und von dort auch wieder
entnommen. In Java ist ein Stack eine Ableitung von Vector mit neuen
Zugriffsfunktionen für die Implementierung des typischen Verhaltens von einem
Stack.
Konstruktor: public Stack();
Hinzufügen neuer Elemente: public Object push(Object item);
Zugriff auf das oberste Element:
public Object pop();
// Zugriff und Entfernen des obersten
Element
public Object peek()
// Zugriff auf das oberste Element
Suche im Stack: public int search(Object o)
// Suche nach beliebigem Element,
// Rueckgabewert: Distanz zwischen gefundenem und
//
obersten Stack−Element bzw. −1,
//
falls das Element nicht da ist.
Test: public boolean empty()
// bestimmt, ob der Stack leer ist
Vector
Stack
public Stack()
public Object push(Object obj)
public synchronized Object pop()
public synchronized Object peek()
public synchronized int search(Object obj)
public boolean empty()
Abb.: Die Klasse Stack
Anwendungen:
1. Umrechnen von Dezimalzahlen in andere Basisdarstellungen
Aufgabenstellung: Defaultmäßig werden Zahlen dezimal ausgegeben. Ein Stapel, der Ganzzahlen
aufnimmt, kann dazu verwendet werden, Zahlen bezogen auf eine andere Basis als 10 darzustellen.
Die Funktionsweise der Umrechnung von Dezimalzahlen in eine Basis eines anderen Zahlensystem
zeigen die folgenden Beispiele:
10
Algorithmen und Datenstrukturen
2810 = 3 ⋅ 8 + 4 = 34 8
7210 = 1 ⋅ 64 + 0 ⋅ 16 + 2 ⋅ 4 + 0 = 10204
5310 = 1 ⋅ 32 + 1⋅ 16 + 0 ⋅ 8 + 1 ⋅ 4 + 0 ⋅ 2 + 1 = 1101012
Mit einem Stapel läßt sich die Umrechnung folgendermaßen unterstützen:
6
1
leerer Stapel
n = 355310
n%8=1
n/8=444
n = 444 10
7
7
4
4
4
1
1
1
n%8=7
n%8=6
n%8=4
n/8=55
n/8=6
n = 5510
n = 610
n/6=0
n = 010
Abb.: Umrechnung von 355310 in 67418 mit Hilfe eines Stapel
Algorithmus zur Lösung der Aufgabe:
1) Die am weitesten rechts stehende Ziffer von n ist n%b. Sie ist auf dem Stapel abzulegen.
2) Die restlichen Ziffern von n sind bestimmt durch n/b. Die Zahl n wird ersetzt durch n/b.
3) Wiederhole die Arbeitsschritte 1) und 2) bis keine signifikanten Ziffern mehr übrig bleiben.
4) Die Darstellung der Zahl in der neuen Basis ist aus dem Stapel abzulesen. Der Stapel ist zu diesem
Zweck zu entleeren.
Implementierung: Das folgende kleine Testprogramm7 realisiert den Algorithmus und benutzt dazu
eine Instanz von Stack.
import java.util.*;
public class PR61210
{
public static void main(String[] args)
{
int zahl = 3553;
// Dezimalzahl
int b
= 8;
// Basis
Stack s = new Stack();
// Stapel
do
{
s.push(new Integer(zahl % b));
zahl /= b;
} while (zahl != 0);
while (!s.empty())
{
System.out.print(s.pop());
}
System.out.println();
}
}
7
pr61210
11
Algorithmen und Datenstrukturen
Ein Stack ist ein Vector. Die Vector−Klasse wird von der Klasse Stack erweitert. Das
ist sicherlich nicht immer besonders sinnvoll. Funktionen, die im Gegensatz zur
Leistungsfähigkeit eines Stapels stehen sind add(), addAll(), addElement(),
capacity(), clear(), clone(), contains(), copyInto(), elementsAt(), .... .
2.2.4 Die Klasse Bitset für Bitmengen
class java.util.BitSet implements Cloneable, Serializable
Die Klasse Bitset bietet komfortable Möglichkeiten zur bitweisen Manipulation von
Daten.
Bitset anlegen und füllen. Mit zwei Methoden lassen sich die Bits des Bitsets leicht
ändern: set(bitNummer) und clear(bitNummer).
Mengenorintierte Operationen. Das Bitset erlaubt mengenorientierte Operationen mit
einer weiteren Menge.
BitSet
public void and(BitSet bs)
public void or(BitSet bs)
public void xor(BitSet bs)
public void andNot(Bitset set)
// löscht alle Bits im Bitset, dessen Bit in set gesetzt sind
public void clear(int index)
// Löscht ein Bit. Ist der Index negativ, kommt es
// zur Auslösung von IndexOutOfBoundsException
public void set(int index)
// Setzt ein Bit. Ist der Index negativ, kommt es
// zur Auslösung von IndexOutOfBoundsException
public boolean get(int index)
// liefert den Wert des Felds am übergebenen Index,
// kann IndexOutOfBoundsException auslösen.
public int size()
public boolean equals(Object o)
// Vergeicht sich mit einem anderen Bitset−Objekt o.
Abb.: Die Klasse BitSet
12
Algorithmen und Datenstrukturen
2.2.5 Die Klasse Hashtable und assoziative Speicher
Eine Hashtabelle (Hashtable) ist ein assoziativer Speicher, der Schlüssel (keys) mit
Werten verknüpft. Die Datenstruktur ist mit einem Wörterbuch vergleichbar. Die
Hashtabelle arbeitet mit Schlüssel/Werte Paaren. Aus dem Schlüssel wird nach einer
Funktion − der sog. Hashfunktion − ein Hashcode berechnet. Dieser dient als Index
für ein internes Array. Dieses Array hat zu Anfang ein feste Grösse. Leider hat
dieses Technik einen entscheidenden Nachteil. Besitzen zwei Wörter denselben
Hashcode, dann kommt es zu einer Kollision. Auf ihn muß die Datenstruktur
vorbereitet sein. Hier gibt es verschiedene Lösungsansätze. Die unter Java
implementierte Variante benutzt eine verkettete Liste (separate Chaining). Falls eine
Kollision auftritt, so wird der Hashcode beibehalten und der Schlüssel bzw. Wert in
einem Listenelement an den vorhandenen Eintrag angehängt. Wenn allerdings
irgendwann einmal eine Liste durchsucht werden muß, dann wird die Datenstruktur
langsam. Ein Maß für den Füllgrad ist der Füllfaktor (Load Factor). Dieser liegt
zwischen 0 und 100 %. 0 bedeutet: kein Listenelement wird verwendet. 100 %
bedeutet: Es ist kein Platz mehr im Array und es werden nur noch Listen für alle
zukommenden Werte erweitert. Der Füllfaktor sollte für effiziente Anwendungen nicht
höher als 75% sein. Ist ein Füllfaktor nicht explizit angegeben, dann wird die
Hashtabelle "rehashed", wenn mehr als 75% aller Plätze besetzt sind.
class java.util.Hashtable extends Dictionary implements Map,
Cloneable, Serializable
Erzeugen von einem Objekt der Klasse HashTable:
public Hashtable()
/* Die Hashtabelle enthält eine Kapazität von 11 Einträgen und einen Füllfaktor von 75 % */
public HashTable(int initialCapacity)
/* erzeugt eine Hashtabelle mit einer vorgebenen Kapazität und dem Füllfaktor 0.75 */
public HashTable(int initialCapacity, float loadFactor)
/* erzeugt eine Hashtabelle mit einer vorgebenen Kapazität und dem angegebenen Füllfaktor */
Daten einfügen: public Object put(Object key, Object value)
/* speichert den Schlüssel und den Wert in der Hashtabelle. Falls sich zu dem
Schlüssel schon ein Eintrag in der Hashtabelle befand, so wird dieser
zurückgegeben. Anderenfalls ist der Rückgabewert null. Die Methode ist
vorgegeben vom Interface Map. Es überschreibt die Methode von der Superklasse
Dictionary. */
Daten holen: public Object get(Object key)
Schlüssel entfernen. public Object remove(Object key)
Löschen der Werte. public void clear()
Test. public boolean containsKey(Object key)
// Test auf einen bestimmten Schlüssel
public boolean containsValue(Object value)
// Test auf einen bestimmten Wert
Aufzählen der Elemente. Mit keys() und elements() bietet die Hashtabelle zwei
Methoden an, die eine Aufzählung zurückgeben:
public Enumeration keys()
// liefert eine Aufzählung aller Schlüssel, überschreibt keys() in Dictionary.
public Enumeration elements()
// liefert eine Aufzählung der Werte, überschreibt elements() in Dictionary
Wie üblich liefern beide Iteratoren ein Objekt, welches das Interface Enumeration
implementiert.
Der
Zugriff
erfolgt
daher
mit
Hilfe
der
Methoden
hasMoreElements() und nextElement().
13
Algorithmen und Datenstrukturen
Dictionary
{abstract}
public abstract Object put (Object key, Object value)
publicc abstract Object get(Object key)
public abstract Enumeration elements()
public abstract Enumeration keys()
public abstract int size()
public absztract boolean isEmpty()
public abstract Object remove(Object key)
Hashtable
Map
<< Konstruktor >>
public Hashtable(int initialKapazitaet)
public Hashtable(int initialKapazitaet, float Ladefaktor)
public Hashtable()
<< Methoden >>
public synchronized boolean contains(Object wert)
public synchronized boolean containsKey(Object key)
public synchronized void clear()
public synchronized Object clone()
protected void rehash()
public synchronized String toString()
Properties
<< Konstruktor >>
public Properties()
// legt einen leeren Container an
public Properties(Properties defaults)
// füllt eine Property−Liste mit den angegebenen Default−Werten
<< Methoden >>
public String getProperty(String key)
public String getProperty(String key, String defaultKey)
public synchronized void load(InputStream in) throws IOException
// Hier muß ein InputStream übergeben werden, der die daten der
// Property−Liste zur Verfügung stellt.
public synchronizred void save(OutputStream out, String header)
public void list(PrintStream out)
public void list(PrintWriter out)
public Enumeration propertyNames()
// beschafft ein Enumerations−Objekt mit denen Eigenschaften
// der Property−Liste aufgezählt werden können
Abb.: Die Klassen Hashtable und Properties
Die Klasse Hashtable ist eine Konkretisierung der abstrakten Klasse Dictionary.
Diese Klasse beschreibt einen assoziativen Speicher, der Schlüssel auf Werte
abbildet und über den Schlüsselbegriff einen effizienten Zugriff auf den Wert
ermöglicht. Einfügen und der Zugriff auf Schlüssel erfolgt nicht auf der Basis des
14
Algorithmen und Datenstrukturen
Operators "==", sondern mit Hilfe der Methode "equals". Schlüssel müssen daher
lediglich inhaltlich gleich sein, um als identisch angesehen zu werden.
Bsp. : Hashtabelle zum Test der von Zufallszahlen der Methode Math.random().
8
import java.util.*;
class Zaehler
{
int i = 1;
public String toString()
{
return Integer.toString(i);
}
}
public class Statistik
{
public static void main(String args[])
{
Hashtable h = new Hashtable();
for (int i = 0; i < 10000; i++)
{
// Erzeuge eine Zahl zwischen 0 und 20
Integer r = new Integer((int)(Math.random() * 20));
if (h.containsKey(r))
((Zaehler) h.get(r)).i++;
else h.put(r,new Zaehler());
}
System.out.println(h);
}
}
Die Klasse Hashtable benutzt das Verfahren der Schlüsseltransformation (Hash−
Funktion) zur Abbildung von Schlüsseln auf Indexpostionen eines Arrays. Die
Kapazität der Hash−Tabelle gibt die Anzahl der Elemente an, die insgesamt
untergebracht werden können. Der Ladefaktor zeigt an, bei welchem Füllungsgrad
die Hash−Tabelle vergrößert werden muß. Das Vergrößern erfolgt automatisch, falls
die Anzahl der Elemente innerhalb der Tabelle größer ist als das Produkt aus
Kapazität und Ladefaktor. Seit dem JDK 1.2 darf der Ladefaktor auch größer als 1
sein. In diesem Fall wird die Hash−Tabelle erst dann vergrößert, wenn der
Füllungsgrad größer als 100% ist und bereits ein Teil der Elemente in den
Überlaufbereichen untergebracht wurde.
Die Klasse Hashtable ist eine besondere Klasse für Wörterbücher. Ein Wörterbuch
ist eine Datenstruktur, die Elemente miteinander assoziiert. Das Wörterbuchproblem
ist das Problem, wie aus dem Schlüssel möglichst schnell der zugehörige Wert
konstruiert wird. Die Lösung des Problems ist: Der Schlüssel wird als Zahl kodiert
(Hashcode) und dient in einem Array als Index. An einem Index hängen dann noch
die Werte mit gleichem Hashcode als Liste an.
8
vgl. pr13215
15
Algorithmen und Datenstrukturen
2.2.6 Die abstrakte Klasse Dictionary
Die Klasse Dictionary ist eine abstrakte Klasse, die Methoden anbietet, wie
Objekte (also Schlüssel und Wert) miteinander assoziiert werden:
public abstract Object put(Object key,Object value)
// fügt den Schlüssel key mit dem verbundenen Wert value in das Wörterbuch
// ein
public abstract Object get(Object key)
//
//
//
//
liefert das zu key gehörende Objekt zurück. Falls kein Wert mit dem
Schlüssel verbunden ist, so liefert get() eine null. Eine null als
Schlüssel oder Wert kann nicht eingesetz werden. In put() würde das zu
einer NullPointerException führen.
public abstract Object remove(Object key)
// entfernt ein Schlüssel/Wertepaar aus dem Wörterbuch. Zurückgegeben wird
// der assoziierte Wert.
public abstract boolean isEmpty()
// true, falls keine Werte im Wörterbuch
public int size()
gibt zurück, wie viele Elemente aktuell im Wörterbuch sind.
public abstract Enumeration keys()
// liefert eine Enumeration für alle Schlüssel
public abstract Enumeration elements()
// liefert eine Enumeration über alle Werte.
2.2.7 Die Klasse Properties
Die Properties Klasse ist eine Erweiterung von Hashtable. Ein Properties Objekt
erweitert die Hashtable um die Möglichkeit, sich unter einem wohldefinierten Format
über einen Strom zu laden und zu speichern.
Erzeugen. public Properties()
// erzeugt ein leeres Propertes Objekt ohne Worte.
public Properties(Properties p)
// erzeugt ein leeres Properties Objekt mit Standard−werten aus den
// übergebenen Properties
Die Methode getProperty(). public String getProperty(String s)
// sucht in den Properties nach der Zeichenkette
public String getProperty(String key, String default)
// sucht in den Properties nach der Zeichenkette key. Ist dieser nicht
// vorhanden, wird der String default zurückgegeben
Eigenschaften ausgeben. Die Methode list() wandert durch die Daten und gibt
sie auf einem PrintWriter aus:
public void list(PrintWriter pw)
// listet die Properties auf dem PrintWriter aus.
16
Algorithmen und Datenstrukturen
2.2.8 Collection API
Die Java 2 Plattform hat Java erweitert um das Collection API. Anstatt Collection
kann man auch Container (Behälter) sagen. Ein Container ist ein Objekt, das
wiederum Objekte aufnimmt und die Verantwortung für die Elemente übernimmt. Im
"util"−Paket befinden sich sechs Schnittstellen, die grundlegende Eigenschaften
der Containerklassen definieren.
Das in Java 1.2 enthaltene Collections Framework beinhaltet im Wesentlichen drei
Grundformen: Set, List und Map. Jede dieser Grudformen ist als Interface
implementiert. Die Interfaces List und Set sind direkt aus Collection abgeleitet.
Es gibt auch noch eine abstrakte Implementierung des Interface, mit dessen Hilfe
das Erstellen eigener Collections erleichtert wird. Bei allen Collections, die das
Interface Collection implementieren, kann ein Iterator zum Durchlaufen der Elemente
mit der Methode "iterator()" beschafft werden.
Zusätzlich fordert die JDK 1.2−Spezifikation für jede Collection−Klasse zwei
Konstruktoren:
− Einen parameterlosen Konstruktor zum Anlegen einer neuen Collection.
− Ein mit einem einzigen Collection−Argument ausgestatteter Konstruktor, der eine neue Collection
anlegt und mit den Elementen der als Argument übergebenen Collection auffüllt.
2.2.8.1 Die Schnittstellen Collection, Iterator, Comparator
Das Interface Collection bildet die Basis der Collection−Klasse und −Interfaces
des JDK 1.2. Alle Behälterklassen implementieren das Collection Interface und
geben den Klassen damit einen äußeren Rahmen.
17
Algorithmen und Datenstrukturen
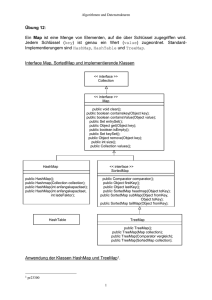
Das Interface Collection
<< interface >>
Collection
public void clear();
// Optional: Löscht alle Elemente in dem Container. Eird dies vom Container nicht unterstützt,
// kommt es zur UnSupportedOperationException
public boolean add(Object o);
// Optional: Fügt ein Objekt dem Container hinzu und gibt true zurück, falls sich das Element
// einfügen läßt. Gibt false zurück, falls schon ein Objektwert vorhanden ist und doppelte Werte
// nicht erlaubt sind.
public boolean addAll(Collection c);
// fügt alle Elemente der Collection c dem Container hinzu
public boolean remove(Object o);
// Entfernen einer einzelnen Instanz. Rückgabewert ist true, wenn das Element gefunden und
// entfernt werden konnte
public boolean removeAll(Collection c);
// Oprtional: Entfernt alle Objekte der Collection c aus dem Container
public boolean contains(Object o);
// liefert true, falls der Container das Element enthält
// Rückgabewert ist true, falls das vorgegebene Element gefunden werden konnte
public boolean containsAll(Collection c);
// liefert true, falls der Container alle Elemente der Collection c enthält.
public boolean equals(Object o);
// vergleicht das angegebene Objekt mit dem Container, ob die gleichen Elemente vorkommen.
public boolean isEmpty();
// liefert true, falls der Container keine Elemente enthält
public int size();
// gibt die Größe des Containers zurück
public boolean retainAll(Collection c);
public Iterator iterator();
publicObject [] toArray();
// gibt ein Array mit Elementen des Containers zurück
public Object [] toArray(Object [] a);
public int hashCode();
// liefert den Hashwert des Containers
public String toString()
// Rückgabewert ist die Zeichenketten−Repräsentation der Kollektion.
Abb.: Das Interface Collection
Die abstrakte Basisklasse AbstractCollection implementiert die Methoden des
Interface Collection (ohne iterator() und size()). AbstractCollection ist
die Basisklasse von AbstractList und AbstractSet.
18
Algorithmen und Datenstrukturen
Das Interface Iterator
<< interface >>
Iterator
public boolean hasNext();
// gibt true zurück, wenn der Iterator mindestens ein weiteres Element enthält.
public Object next();
// liefert das nächste Element bzw. löst eine Ausnahme des Typs NoSuchElementException
// aus, wenn es keine weiteren Elemente gibt
public void remove();
// entfernt das Element, das der Iterator bei next() geliefert hat.
Abb.:
Bei allen Collections, die das Interface Collection implementieren, kann ein Iterator
zum Durchlaufen der Elemente mit der Methode "iterator()" beschafft werden.
Das Interface Comparator
Vergleiche zwischen Objekten werden mit speziellen Objekten vorgenommen, den
Comparatoren. Ein konkreter Comparator implementiert die folgende Schnittstelle.
<< interface >>
java.util.Comparator
public int compare(Object o1, Object o2)
// vergleicht 2 Argumente auf ihre Ordnung
public boolean equals(Object arg)
// testet, ob zwei Objekte bzgl. des Comparator−Objekts gleich sind
Abb.
19
Algorithmen und Datenstrukturen
2.2.8.2 Die Behälterklassen und Schnittstellen des Typs List
Behälterklassen des Typs List fassen eine Menge von Elementen zusammen, auf
die sequentiell oder über Index (−positionen) zugegriffen werden kann. Wie Vektoren
der Klasse Vector hat das erste Element den Index 0 und das letzte den Index
"size() − 1". Es ist möglich an einer beliebigen Stelle ein Element einzufügen
oder zu löschen. Die weiter hinten stehenden Elemente werden dann entsprechend
weiter nach rechts bzw. nach links verschoben.
9
Das Interface List
10
<< interface >>
List
public void add(int index, Object element);
// Einfügen eines Elements an der durch Index spezifizierten Position
public boolean add(Object o);
// Anhängen eines Elements ans Ende der Liste
// Rückgabewert ist true, falls die Liste durch den Aufruf von add verändert wurde. Er ist false,
// wenn die Liste nicht verändert wurde. Das kann bspw. der Fall sein, wenn die Liste keine
// Duplikate erlaubt und ein bereits vorhandenes Element noch einmal eingefügt werden soll.
// Konnte das Element aus einem anderen Grund nicht eingefügt werden, wird eine Ausnahme
// des Typs UnsupportedOperationException, CallsCastException oder IllegalArgumentException
// ausgelöst
public boolean addAll(Collection c);
// Einfügen einer vollständigen Collection in die Liste. Der Rückgabewert ist true, falls die Liste
// durch den Ausfruf von add veränder wurde
public boolean addAll(int index, Collection c)
public void clear();
public boolean equals(Object object);
public boolean contains(Object element);
public boolean containsAll(Collection collection);
public Object remove(int index)
public boolean remove(Object element);
public boolean removeAll(Collection c);
// Alle Elemente werden gelöscht, die auch in der als Argument angebenen
// Collection enthalten sind.
public boolean retainAll(Collection c);
// löscht alle Elemente außer den in der Argument−Collection enthaltenen
public Object get();
public int hashCode();
public Iterator iterator();
public ListIterator listIterator():
public ListIterator listIterator(int startIndex);
public Object set(int index, Obeject element);
public List subList(int fromIndex, int toIndex);
public Object [] toArray();
public Object [] toArray(Object [] a);
Abb.:
Auf die Elemente einer Liste läßt sich mit einem Index zugreifen und nach
Elementen läßt sich mit linearem Aufwand suchen. Doppelte Elemente sind erlaubt.
9
seit Java 1.2 implementiert die Klasse Vector die Schnittstelle List
Da ebenfalls das AWT−Paket eine Klasse mit gleichen namen verwendet, muß der voll qualifizierte Name
in Anwendungen benutzt werden.
10
20
Algorithmen und Datenstrukturen
Die Schnittstelle List, die in ArrayList und LinkedList eine Implementierung findet,
erlaubt sequentiellen Zugriff auf die gespeicherten gespeicherten Elemente. Das
Interface List wird im JDK von verschiedenen Klassen implementiert:
AbstractList
ist eine abstrakte Basisklasse (für eigene List−Implementierungen), bei der alle
Methoden die Ausnahme UnsupportedException auslösen und diverse
Methoden abstract
deklariert sind. Die direkten Subklassen sind
AbstractSequentialList,
ArrayList
und
java.util.Vector.
AbstractList implementiert bereits viele Methoden für die beiden Listen−
Klassen :
11
abstract class AbstractList extends AbstractCollection implements List
<< Methoden >>
public void add(int index, Object element)
// Optional: Fügt ein Objekt an der spezifizierten stelle ein
public boolean add(Object o)
// Optional: Fügt das Element am Ende an
public boolean addAll(int index, Collection c)
// Optional: Fügt alle Elemente der Collection ein
public void clear()
// Optional: Löscht alle Elemente
public boolean equals(Object o)
// vergleicht die Liste mit dem Objekt
public abstract Object get(int index)
// liefert das Element an dieser Stelle
int hashCode()
// liefert HashCode der Liste
int indexOf(Object o)
// liefert Position des ersten Vorkommens für o oder −1,
// wenn das Element nicht existiert.
Iterator iterator()
// liefert den Iterator. Überschreibt die Methode AbstractCollection,
// obwohl es auch listIterator() für die spezielle Liste gibt. Die Methode
// ruft aber listIterator() auf und gibt ein ListIterator−Objekt zurück
Object remove(int index)
// löscht ein Element an Position index.
protected void removeRange(int fromIndex, int toIndex)
// löscht Teil der Liste von fromIndex bis toIndex. fromIndex wird mitgelöscht,
// toIndex nicht.
public Object set(int index, Object element)
// Optional. Ersetzt das Element an der Stelle index mit element.
public List subList(int fromIndex, int toIndex)
// liefert Teil einer Liste fromIndex (einschließlich) bis toIndex (nicht mehr dabei)
Abb.:
AbstractSequentialList
bereitet die Klasse LinkedList darauf vor, die Elemente in einer Liste zu verwalten
und nicht wie ArrayList in einem internen Array.
LinkedList
realisiert die doppelt verkettete, lineare Liste und implementiert List.
ArrayList
11 Beim aufruf einer optionalen Methode, die von der Subklasse nicht implementiert wird, führt zur
UnsupportedOperationException.
21
Algorithmen und Datenstrukturen
implementiert die Liste als Feld von Elementen und implementiert List. Da Arraylist
ein Feld ist, ist der Zugriff auf ein spezielles Element sehr schnell. Eine LinkedList
muß aufwendiger durchsucht werden. Die verkettete Liste ist aber deutlich im Vorteil,
wenn Elemente gelöscht oder eingefügt werden.
22
Algorithmen und Datenstrukturen
<< interface >>
Collection
<< interface >>
List
LinkedList
ArrayList
<< Konstruktor >>
public LinkedList();
public LinkedList(Collection collection);
<< Konstruktor
public ArrayList();
public ArrayList(Collection collection);
public ArrayList(int anfangsKapazitaet);
<< Methoden >>
public void addFirst(Object object);
public void addLast(Object object);
public Object getFirst();
public Object getLast();
public Object removeFirst();
public Object removeLast();
<< Methoden >>
protected void removeRange
(int fromIndex, int toIndex)
// löscht Teil der Liste von
// fromIndex bis toIndex. fromIndex wird
// mitgelöscht, toIndex nicht.
Vector
Abb.
Das Interface ListIterator
<< interface >>
ListIterator
public boolean hasPrevious();
// bestimmt, ob es vor der aktuellen Position ein weiteres Element gibt, der Zugriff ist mit
// previous möglich
public boolean hasNext();
public Object next();
public Object previous();
public int nextIndex();
puplic int previousIndex();
public void add(Object o);
// Einfügen eines neuen Elements an der Stelle der Liste, die unmittelbar vor dem nächsten
// Element des Iterators liegt
public void set(Object o);
// erlaubt, das durch den letzten Aufruf von next() bzw. previous() beschaffene Element zu
// ersetzen
public void remove();
Abb.:
ListIterator ist eine Erweiterung von Iterator. Die Schnittstelle fügt noch
Methoden hinzu, damit an aktueller Stelle auch Elemente eingefügt werden können.
23
Algorithmen und Datenstrukturen
Mit einem ListIterator läßt sich rückwärts laufen und auf das vorgehende
Element zugreifen.
Bsp.:
1. Simulation einer Schlange12
Eine verkettete Liste hat neben den normalen Funktionen aus AbstractList noch weitere
Hilfsmethoden zur Implementierung von einem Stack oder einer Schlange. Es handelt sich dabei um
die Methoden addFirst(), addLast(), getFirst(), getLast() und removeFirst().
import java.util.*;
public class ListBsp
{
public static void main(String [] args)
{
LinkedList schlange = new LinkedList();
schlange.add("Thomas");
schlange.add("Andreas");
schlange.add("Josef");
System.out.println(schlange);
schlange.removeFirst();
schlange.removeFirst();
System.out.println(schlange);
}
}
2. Entfernen von Duplikaten13
import java.util.*;
public class EntfDupl
{
public static void main(String args[])
{
int [] a = { 1, 7, 7, 1, 5, 1, 2, 7, 2, 1, 6, 6, 3, 6, 7 };
LinkedList l = new LinkedList();
for (int i = 0; i < a.length; i++)
{ l.add(new Integer(a[i])); }
System.out.println(l);
int i = 0;
do
{
int aktWert = ((Integer) l.get(i)).intValue();
i++;
if (i == l.size()) break;
int j = i;
do
{
int wert = ((Integer) l.get(j)).intValue();
if (wert == aktWert) l.remove(j);
j++;
} while (j < l.size());
System.out.println(l);
} while (i < l.size());
}
}
12
13
Vgl. pr22220
vgl. pr22220
24
Algorithmen und Datenstrukturen
2.2.8.3 Behälterklassen des Typs Set
Ein Set ist eine Menge, in der keine doppelten Einträge vorkommen können. Set hat
die gleichen Methoden wie Collection. Standard−Implementierung für Set sind das
unsortierte HashSet (Array mit veränderlicher Größe) und das sortierte TreeSet
(Binärbaum).
Bsp. :
14
import java.util.*;
public class SetBeispiel
{
public static void main(String args [])
{
Set set = new HashSet();
set.add("Gerhard");
set.add("Thomas");
set.add("Michael");
set.add("Peter");
set.add("Christian");
set.add("Valentina");
System.out.println(set);
Set sortedSet = new TreeSet(set);
System.out.println(sortedSet);
}
}
14
Vgl. pr13230
25
Algorithmen und Datenstrukturen
<< interface >>
Collection
<< interface >>
Set
public boolean add(Object element);
public boolean addAll(Collection collection);
public void clear();
public boolean equals(Object object);
public boolean contains(Object element);
public boolean containsAll(Collection collection);
public int hashCode();
public Iterator iterator();
public boolean remove(Object element);
public boolean removeAll(Collection collection);
public boolean retainAll(Collection collection);
public int size();
public Object[] toArray();
public Object[] toArray(Object[] a);
HashSet
<< interface >>
SortedSet
public HashSet();
public HashSet(Collection collection);
public HashSet(int anfangskaazitaet);
public HashSet(int anfangskapazitaet,
int ladeFaktor);
public Object first();
public Object last();
public SortedSet headSet(Object toElement);
public SortedSet subSet(Object fromElement,
Object toElement);
public SortedSet tailSet(Object fromElement);
public Comparator comparator();
public Object fisrt();
public Object last();
TreeSet15
public TreeSet()
public TreeSet(Collection collection);
public TreeSet(Comparator vergleich);
public TreeSet(SortedSet collection);
Die Schnittstelle Set
Ist eine im mathematischen Sinne definierte Menge von Objekten. Die Reihenfolge
wird durch das Einfügen festgelegt. Wie von mathematischen Mengen bekannt, darf
ein Set keine doppelten Elemente enthalten. Besondere Beachtung muß Objekten
geschenkt werden, die ihren Wert nachträglich ändern. Die kann ein Set nicht
kontrollieren. Eine Menge kann sich nicht selbst als Element enthalten.
15 implementiert die sortierte Menge mit Hilfe der Klasse TreeMap, verwendet einen Red−Black−Tree als
Datenstruktur
26
Algorithmen und Datenstrukturen
Zwei Klassen ergeben sich aus Set: die abstrakte Klasse AbstractSet und die
konkrete Klasse HashSet.
Die Schnittstelle SortedSet
erweitert Set so, daß Elemente sortiert ausgelesen werden können. Das
Sortierkriterium wird durch die Hilfsklasse Comparator gesetzt.
2.2.8.4 Behälterklassen des Typs Map
Ein Map ist eine Menge von Elementen, auf die über Schlüssel zugegriffen wird.
Jedem Schlüssel (key) ist genau ein Wert (value) zugeordnet. Standard−
Implementierungem sind HashMap, HashTable und TreeMap.
27
Algorithmen und Datenstrukturen
Interface Map, SortedMap und implemetierende Klassen
<< interface >>
Collection
<< interface >>
Map
public void clear();
public boolean containskey(Object key);
public boolean containsValue(Object value);
public Set entrySet();
public Object get(Object key);
public boolean isEmpty();
public Set keySet();
public Object remove(Object key);
public int size();
public Collection values();
HashMap
public HashMap();
public Hashmap(Collection collection);
public HashMap(int anfangskapazitaet);
public HashMap(int anfangskapazitaet,
int ladeFaktor);
<< interface >>
SortedMap
public Comparator comparator();
public Object firstKey();
public Object lastKey();
public SortedMap headmap(Object toKey);
public SortedMap subMap(Object fromKey,
Object toKey);
public SortedMap tailMap(Object fromKey);
Hashtable
TreeMap
public TreeMap();
public TreeMap(Map collection);
public TreeMap(Comparator vergleich);
public TreeMap(SortedMap collection);
Abb.:
Die Schnittstelle Map
Eine Klasse, die Map implementiert, behandelt einen assoziativen Speicher. Dieser
verbindet einen Schlüssel mit einem Wert. Die Klasse Hashtable erbt von Map.
Map ist für die implementierenden Klassen AbstractMap, HashMap, Hashtable,
RenderingHints, WeakHashMap und Attributes das, was die abstrakte Klasse
Dictionary für die Klasse Hashtable ist.
Die Schnittstelle SortedMap
Eine Map kann mit Hilfe eines Kriteriums sortiert werden und nennt sich dann
SortedMap. SortedMap erweitert direkt Map. Das Sortierkriterium wird mit einem
speziellen Objekt, das sich Comparator nennt, gesetzt. Damit besitzt auch der
28
Algorithmen und Datenstrukturen
assoziative Speicher über einen Iterator eine Reihenfolge. Nur die konkrete Klasse
TreeMap implementiert bisher eine SortedMap.
Die abstrakte Klasse AbstractMap implementiert die Schnittstelle Map.
Die konkrete Klasse HashMap implementiert einen assoziativen Speicher, erweitert
die Klasse AbstractMap und implementiert die Schnittstelle Map.
Die konkrete Klasse TreeMap erweitert AbstractMap und implementiert
SortedMap. Ein Objekt von TreeMap hält Elemente in einem Baum sortiert.
Bsp. : Aufbau und Anwendung einer Hash−Tabelle
16
import java.io.*;
import java.util.*;
public class HashTabTest
{
public static void main(String [ ] args)
{
Map map = new HashMap();
String eingabeZeile
= null;
BufferedReader eingabe = null;
try {
eingabe = new BufferedReader(
new FileReader("eing.txt"));
}
catch (FileNotFoundException io)
{
System.out.println("Fehler beim Einlesen!");
}
try {
while ( (eingabeZeile = eingabe.readLine() ) != null)
{
StringTokenizer str = new StringTokenizer(eingabeZeile);
if (eingabeZeile.equals("")) break;
String key
= str.nextToken();
String daten = str.nextToken();
System.out.println(key);
map.put(key,daten);
}
}
catch (IOException ioe)
{
System.out.println("Eingefangen in main()");
}
try {
eingabe.close();
}
catch(IOException e)
{
System.out.println(e);
}
System.out.println("Uebersicht zur Hash−Tabelle");
System.out.println(map);
//h.printHashTabelle();
System.out.println("Abfragen bzw. Modifikationen");
// Wiederauffinden
String eingabeKey = null;
BufferedReader ein = new BufferedReader(
new InputStreamReader(System.in));
System.out.println("Wiederauffinden von Elementen");
while (true)
{
try {
System.out.print("Bitte Schluessel eingeben, ! bedeutet Ende: ");
eingabeKey = ein.readLine();
// System.out.println(eingabeKey);
if (eingabeKey.equals("!")) break;
String eintr = (String) map.get(eingabeKey);
16
vgl. pr23300
29
Algorithmen und Datenstrukturen
if (eintr == null)
System.out.println("Kein Eintrag!");
else
{
System.out.println(eintr);
System.out.println("Soll dieser Eintrag geloescht werden? ");
String antwort = ein.readLine();
// System.out.println(antwort);
if ((antwort.equals("j")) || (antwort.equals("J")))
{
// System.out.println("Eintrag wird entfernt!");
map.remove(eingabeKey);
}
}
}
catch(IOException ioe)
{
System.out.println(eingabeKey +
" konnte nicht korrekt eingelesen werden!");
}
}
System.out.println(map);
System.out.println("Sortierte Tabelle");
Map sortedMap = new TreeMap(map);
System.out.println(sortedMap);
}
}
2.2.8.5 Implementierung von Graphen−Algorithmen mit Behälterklassen
2.2.8.5.1 Kürzeste Pfade in gerichteten, ungewichteten Graphen.
Lösungsbeschreibung. Die
ungewichteten Graphen G:
folgende
Abbildung
k1
k3
zeigt
einen
gerichteten,
k2
k4
k5
k6
k7
Abb.:
Ausgangspunkt ist ein Startknoten s (Eingabeparameter). Von diesem Knoten aus
soll der kürzeste Pfad zu allen anderen Knoten gefunden werden. Es interessiert nur
die Anzahl der Kanten, die in dem Pfad enthalten sind.
Falls für s der Knoten k3 gewählt wurde, kann zunächst am Knoten k3 der Wert 0
eingetragen werden. Die "0" wird am Knoten k3 vermerkt.
k1
k3
k2
k4
k5
30
Algorithmen und Datenstrukturen
0
k6
k7
Abb.: Der Graph nach Markierung des Startknoten als erreichbar
Danach werden alle Knoten aufgesucht, die "eine Einheit" von s entfernt sind. Im
vorliegenden Fall sind das k1 und k6. Dann werden die Knoten aufgesucht, die von s
zwei Einheiten entfernt sind. Das geschieht über alle Nachfolger von k1 und k6. Im
vorliegenden Fall sind es die Knoten k2 und k4. Aus den benachbarten Knoten von k2
und k4 erkennt man, dass k5 und k7 die kürzesten Pfadlängen von drei Knoten
besitzen. Da alle Knoten nun bewertet sind ergibt sich folgenden Bild:
k1
k2
1
k3
2
k4
0
k5
2
1
k6
k7
Abb.: Graph nach Ermitteln aller Knoten mit der kürzeszen Pfadlänge 2
Die hier verwendete Strategie ist unter dem Namen "breadth−first search" bekannt.
Die "Breitensuche zuerst" berücksichtigt zunächst alle Knoten vom Startknoten aus,
die am weitesten entfernt liegenden Knoten werden zuerst ausgerechnet.
Übertragen der Lösungsbeschreibung in Quellcode. Zu Beginn sollte eine Tabelle
mit folgenden Einträgen vorliegen:
k
k1
k2
k3
k4
k5
k6
k7
bekannt
false
false
false
false
false
false
false
dk
∞
∞
0
∞
∞
∞
∞
pk
0
0
0
0
0
0
0
Die Tabelle überwacht den Fortschritt beim Ablauf des Algorithmus und führt Buch
über gewonnene Pfade. Für jeden Knoten werden 3 Angaben in der Tabelle
verwaltet:
− die Distanz dk des jeweiligen Knoten zu dem Startknoten s. Zu Beginn sind alle Knoten von s aus
unerreichbar ( ∞ ). Ausgenommen ist natürlich s, dessen Pfadlänge ist 0 (k3).
− Der Eintrag pk ist eine Variable für die Buchführung (und gibt den Vorgänger im Pfad an).
− Der Eintrag unter "bekannt" wird auf "true" gesetzt, nachdem der zugehörige Knoten erreicht wurde.
Zu Beginn wurden noch keine Knoten erreicht.
Das führt zu der folgenden Knotenbeschreibung:
class Vertex
{
public String
name;
public LinkedList adj;
// Name des Knoten
// Benachbarte Knoten
31
Algorithmen und Datenstrukturen
public boolean
public int
public Vertex
.....
}
bekannt;
dist;
path;
// Kosten
// Vorheriger Knoten auf dem kuerzesten Pfad
Die Grundlage des Algorithmus kann folgendermaßen beschrieben werden:
/*
/*
/*
/*
1
2
3
4
*/
*/
*/
*/
/* 5 */
/* 6 */
/* 7 */
/* 8 */
/* 9 */
void ungewichtet(Vertex s)
{
Vertex v, w;
s.dist = 0;
for (int aktDist = 0; aktDist < ANZAHL_KNOTEN; aktDist++)
for each v
if (!v.bekannt && v.dist == aktDist)
{
v.bekannt = true;
for each w benachbart_zu v
if (w.dist == INFINITY)
{
w.dist = aktDist + 1;
w.path = v;
}
}
}
Der Algorithmus deklariert schrittweise je nach Distanz (d = 0, d = 1, d= 2 ) die
d = ∞ auf die Distanz
Knoten als bekannt und setzt alle benachbarten Knoten von w
d w = d + 1.
2
Die Laufzeit des Algorithmus liegt bei
O( V )
. Die Ineffizienz kann beseitigt werden:
17
d ≠∞
. Einigen Knoten wurde dv = aktDist
Es gibt nur zwei unbekannte Knotentypen mit v
zugeordnet, der Rest zeigt dv = aktDist + 1. Man braucht daher nicht die ganze Tabelle, wie es
in Zeile 3 und Zeile 4 beschrieben ist, nach geeigneten Knoten zu durchsuchen. Am einfachsten ist
es, die Knoten in zwei Schachteln einzuordnen. In die erste Schachtel kommen Knoten, für die gilt: dv
= aktDist. In die zweite Schachtel kommen Knoten, für die gilt: dv = aktDist + 1. In Zeile 3 und
Zeile 4 kann nun irgendein Knoten aus der ersten Schachtel herausgegriffen werden. In Zeile 9 kann
w der zweiten Schachtel hinzugefügt werden. Wenn die äußere for−Schleife terminiert ist die erste
Schachtel leer, und die zweite Schachtel kann nach der ersten Schachtel für den nächsten Durchgang
übertragen werden.
Durch Anwendung einer Schlange (Queue) kann das Verfahren verbessert werden.
Am Anfang enthält diese Schlange nur Knoten mit Distanz aktDist. Benachbarte
Knoten haben die Distanz aktDist + 1 und werden "hinten" an die Schlange
angefügt. Damit wird garantiert, daß zuerst alle Knoten mit Distanz aktDist
bearbeitet werden. Der verbesserte Algorithmus kann in Pseudocode so formuliert
werden:
/* 1 */
/* 2 */
/* 3 */
/*
/*
/*
/*
17
4
5
6
7
*/
*/
*/
*/
void ungewichtet(Vertex s)
{
Queue q;
Vertex v, w;
q = new Queue();
q.enqueue(s); s.dist = 0;
while (!q.isEmpty())
{
v = q.dequeue();
v.bekannt = true; // Wird eigentlich nicht mehr benoetigt
for each w benachbart_zu v
if (w.dist == INFINITY)
{
wegen der beiden verschachtelten for−Schleifen
32
Algorithmen und Datenstrukturen
/* 8 */
/* 9 */
/*10 */
w.dist = v.dist + 1;
w.path = v;
q.enqueue(w);
}
}
}
Die folgende Tabelle zeigt, wie sich die Daten der Tabelle während der Ausführung
des Algorithmus ändern:
Anfangszustand
k
bekannt dk
k1
false
k2
false
k3
false
k4
false
k5
false
k6
false
k7
false
Q: k3
pk
∞
∞
0
0
0
0
0
0
0
0
∞
∞
∞
∞
k2 aus der Schlange
k
bekannt dk
k1
true
k2
true
k3
true
k4
false
k5
false
k6
true
k7
false
Q: k4, k5
1
2
0
2
3
1
pk
k3
k1
0
k1
k2
k3
0
∞
k3 aus der Schlange
bekann dk
pk
t
false
1
k3
∞
false
0
true
0
0
∞ 0
false
∞ 0
false
false
1
k3
∞ 0
false
Q: k1, k6
k4 aus der Schlange
bekann dk
pk
t
true
1
k3
true
2
k1
true
0
0
true
2
k1
false
3
k2
true
1
k3
false
3
k4
Q: k5, k7
k1 aus der Schlange
bekannt dk
pk
true
1
false
2
true
0
false
2
∞
false
false
1
∞
false
Q: k6, k2, k4
k3
k1
0
k1
0
k3
0
k5 aus der Schlange
bekannt dk
pk
true
true
true
true
true
true
false
Q: k7
1
2
0
2
3
1
3
k3
k1
0
k1
k2
k3
k4
k6 aus der Schlange
bekann dk
pk
t
true
1
k3
false
2
k1
true
0
0
false
2
k1
∞
false
0
true
1
k3
∞ 0
false
Q: k2, k4
K7 aus der Schlange
bekann dk
pk
t
true
1
k3
true
2
k1
true
0
0
true
2
k1
true
3
k2
true
1
k3
true
3
k4
Q: leer
Abb.:Veränderung der Daten während der Ausführung des Algorithmus zum kürzesten Pfad
Implementierung .
18
class Vertex
{
String
name;
// Name des Knoten
LinkedList adj;
// Benachbarte Knoten
int
dist;
// Kosten
Vertex
path;
// Vorheriger Knoten auf dem kuerzesten Pfad
// Konstruktor
public Vertex( String nm )
{ name = nm; adj = new LinkedList( ); reset( ); }
// Methode
public void reset( )
{ dist = Graph.INFINITY; path = null; }
}
Über die Instanzvariable adj wird die Liste der benachbarten Knoten geführt, dist
enthält die Kosten, path den Vorgängerknoten vom kürzsten Pfad. Identifiziert wird
der Knoten durch einen Namen (Typ: String).
Die Klasse Graph implementiert die Methode ungewichtet(). Die Schlange in
dieser Liste wird über eine LinkedList mit den Methoden removeFirst() und
addLast() simuliert. Zum Aufbau des Graphen (Adjazenzliste) dient die Methode
18
vgl.: pr22850
33
Algorithmen und Datenstrukturen
addEdge(). Die Kanten werden aus einer Textdatei, die je Zeile ein Knotenpaar
(source, destination) umfaßt. Über die Hashmap vertexMap werden die
Referenzen zu den Knoten hergestellt.
public class Graph
{
public static final int INFINITY = Integer.MAX_VALUE;
private HashMap vertexMap = new HashMap( ); // Abbildung der Knoten
// Methode Hinzufuegen Kante
public void addEdge(String sourceName,String destName )
{
Vertex v = getVertex(sourceName);
Vertex w = getVertex(destName);
v.adj.add( w );
}
// Ausgabe des Pfads
public void printPath(String destName) throws NoSuchElementException
{
Vertex w = (Vertex) vertexMap.get(destName);
if( w == null )
throw new NoSuchElementException( "Destination vertex not found" );
else if( w.dist == INFINITY )
System.out.println( destName + " is unreachable" );
else
{
printPath( w );
System.out.println( );
}
}
// Falls vertexName nicht da ist, fuege den Knoten
// mit diesem Namen in die vertexMap (Adjazenzliste).
// In jedem Fall: Rueckgabe des Knoten.
private Vertex getVertex(String vertexName)
{
Vertex v = (Vertex) vertexMap.get(vertexName);
if( v == null )
{
v = new Vertex(vertexName);
vertexMap.put(vertexName, v);
}
return v;
}
private void printPath(Vertex dest)
{
if( dest.path != null )
{
printPath( dest.path );
System.out.print( " to " );
}
System.out.print( dest.name );
}
private void clearAll( )
{
for( Iterator itr = vertexMap.values( ).iterator( ); itr.hasNext( ); )
( (Vertex)itr.next( ) ).reset( );
}
public void ungewichtet( String startName ) throws NoSuchElementException
{
clearAll( );
Vertex start = (Vertex) vertexMap.get(startName);
if( start == null )
throw new NoSuchElementException( "Startknoten wurde nicht gefunden" );
LinkedList q = new LinkedList( ); // Schlange fuer breadth search first
q.addLast(start); start.dist = 0;
while( !q.isEmpty( ) )
{
Vertex v = (Vertex) q.removeFirst( );
for( Iterator itr = v.adj.iterator( ); itr.hasNext( ); )
{
Vertex w = (Vertex) itr.next( );
if( w.dist == INFINITY )
{
34
Algorithmen und Datenstrukturen
w.dist = v.dist + 1;
w.path = v;
q.addLast( w );
}
}
}
}
/*
* Verarbeitung einer Anforderung;
* Rueckgabe false, falls Dateiende.
*/
public static boolean processRequest(BufferedReader in, Graph g)
{
String startName = null;
String destName = null;
try
{
System.out.println( "Starknoten:" );
if( (startName = in.readLine( ) ) == null )
return false;
System.out.println( "Zielknoten:" );
if( ( destName = in.readLine( ) ) == null )
return false;
g.ungewichtet(startName);
g.printPath(destName);
}
catch( Exception e )
{ System.err.println( e ); }
return true;
}
/*
* Eine main()−Routine, die
* 1. Eine Datei liest, die Kanten enthaelt
*
(Der Dateiname wird als Parameter ueber die
*
Kommandozeile eingegeben);
* 2. den Graphen aufbaut;
* 3. wiederholt 2 Knoten anfordert und
*
den Algorithmus zur Berechnung der kuerzesten Pfade
*
in Gang setzt.
* Die Datei besteht aus Zeilen mit dem Format
*
Quelle (source) Ziel (destination).
*/
public static void main( String [ ] args )
{
Graph g = new Graph( );
try
{
FileReader din = new FileReader(args[0]);
BufferedReader graphFile = new BufferedReader(din);
// Lies die Kanten und fuege ein
String zeile;
while( ( zeile = graphFile.readLine( ) ) != null )
{
StringTokenizer st = new StringTokenizer(zeile);
try
{
if( st.countTokens( ) != 2 )
throw new Exception( );
String source = st.nextToken( );
String dest
= st.nextToken( );
g.addEdge(source, dest);
}
catch( Exception e )
{ System.err.println( e + " " + zeile ); }
}
}
catch( Exception e )
{ System.err.println( e ); }
System.out.println( "File read" );
BufferedReader in = new BufferedReader(
new InputStreamReader( System.in ) );
while( processRequest( in, g ) )
;
35
Algorithmen und Datenstrukturen
}
}
2.2.8.5.2 Berechnung der kürzesten Pfadlängen in gewichteten Graphen (Algorithmus
von Dijkstra)
1. Dijkstras Algorithmus zur Berechnung der kürzesten Wege
Gegeben ist ein gerichteter Graph G mit Knotenmenge V und Kantenmenge E. Jede
Kante e kat eine nichtnegative Länge, Außerdem ist ein Knoten s (Standort)
gegeben.
Gesucht ist der kürzeste Weg von s nach v für jeden Knoten v ∈V des Graphen.
Vorausgesetzt ist, dass jeder Knoten v ∈V durch wenigstens einen Weg von s aus
erreichbar ist. Für den kürzesten Weg soll die Länge ermittelt werden.
Lösungsbeschreibung. Die Lösung stützt sich auf die Berechnung der kürzesten
Pfadlängen in ungewichteten Graphen ab. Im Algorithmus von Dijkstra werden auch
die Daten über "bekannt", dv (kürzeste Pfadlänge) und pv (letzter Knoten, der eine
Veränderung von dv verursacht hat) verwaltet.
Es wird eine Menge S von Knoten betrachtet und schrittweise vergrößert, für die der
kürzeste Weg von s aus bereits bekannt ist. Jedem Knoten v ∈V wird ein Distanz
d(v) zugeordnet. Anfangs ist d(s) = 0 und für alle von s verschiedenen Knoten v ∈V
ist d v = ∞ , und S ist leer. Dann wird S nach dem Prinzip "Knoten mit kürzester
19
Distanz von s zuerst" schrittweise folgendermaßen vergrößert, bis S alle Knoten V
des Graphen enthält:
1. Wähle Knoten v ∈ V
2. Nimm v zu S hinzu
S mit minimaler Distanz
w∉ S , ersetze d(w) durch
3. Für jede Kante vw von einem Knoten v zu einem Knoten
min({d ( v), d (v) + c (v, w)})
Der folgende Graph
2
k1
k2
4
1
3
10
2
2
k3
k4
5
8
k5
4
k6
6
k7
1
Abb.: Graph nach Ermitteln aller Knoten mit der kürzeszen Pfadlänge 2
mit der Knotenbeschreibung
19
vgl. 1.
36
Algorithmen und Datenstrukturen
class Vertex
{
....
public LinkedList adj;
// Benachbarte Knoten
public boolean
bekannt; //
// Kosten
public DistType20 dist;
public Vertex
path;
// Vorheriger Knoten auf dem kuerzesten Pfad
...
}
führt zu der folgende Initialisierung:
k
k1
k2
k3
k4
k5
k6
k7
bekannt
false
false
false
false
false
false
false
dk
0
∞
∞
∞
∞
∞
∞
pk
null
null
null
null
null
null
null
Abb.: Anfangszustand der Tabelle mit den Daten für den Algorithmus von Dijkstra
Der erste Knoten (Start) ist der Knoten k1 mit Pfadlänge 0. Nachdem k1 bekannt ist,
ergibt sich folgendes Bild:
20
DistType ist wahrscheinlich int
37
Algorithmen und Datenstrukturen
k
k1
k2
k3
k4
k5
k6
k7
bekannt
true
false
false
false
false
false
false
dk
0
2
∞
1
∞
∞
∞
pk
null
k1
null
k1
null
null
null
Abb.: Zustand der Tabelle nach "k1 ist bekannt"
"k1" beitzt die Nachbarknoten: k2 und k4. "k4" wird gewählt und als bekannt markiert.
Die Knoten k3, k5, k6 und k7 sind jetzt die benachbarten Knoten.
38
Algorithmen und Datenstrukturen
k
k1
k2
k3
k4
k5
k6
k7
bekannt
true
false
false
true
false
false
false
dk
0
2
3
1
3
9
5
pk
null
k1
k4
k1
k4
k4
k4
Abb.: Zustand der Tabelle nach "k4 ist bekannt"
"k2" wird gewählt. "k4" ist benachbart, aber schon bekannt. "k5" ist ebenfalls
benachbart, wir aber nicht ausgerichtet, da die Kosten von "k2" aus 2 +10 = 12 sind
und ein Pfad der Länge 3 schon bekannt ist
k
k1
k2
k3
k4
k5
k6
k7
bekannt
true
true
false
true
false
false
false
dk
0
2
3
1
3
9
5
pk
null
k1
k4
k1
k4
k4
k4
Abb.: Zustand der Tabelle nach "k2 ist bekannt"
Der nächste ausgewählte Knoten ist "k5" (ohne Ausrichtungen), danach wird k3
gewählt. Die Wahl von "k3" bewirkt die Ausrichtung von "k6"
k
k1
k2
k3
k4
k5
k6
k7
bekannt
true
true
true
true
true
false
false
dk
0
2
3
1
3
8
5
pk
null
k1
k4
k1
k4
k3
k4
Abb.: Zustand der Tabelle "k5 ist bekannt" und (anschließend) "k3 ist bekannt".
"k7" wird gewählt. Daraus resultiert folgende Tabelle:
39
Algorithmen und Datenstrukturen
k
k1
k2
k3
k4
k5
k6
k7
bekannt
true
true
true
true
true
false
true
dk
0
2
3
1
3
6
5
pk
null
k1
k4
k1
k4
k7
k4
Abb.: Zustand der Tabelle "k7 ist bekannt".
Schließlich bleibt nur noch k6 übrig. Das ergibt dann die folgende Abschlußtabelle:
k
k1
k2
k3
k4
k5
k6
k7
bekannt
true
true
true
true
true
true
true
dk
0
2
3
1
3
6
5
pk
null
k1
k4
k1
k4
k7
k4
Abb.: Zustand der Tabelle nach "k6 ist bekannt".
Der Algorithmus, der diese Tabellen
folgendermaßen beschrieben werden:
berechnet,
kann
(in
Pseudocode)
void dijkstra(Vertex s)
{
Vertex v, w;
/* 1 */
s.dist = 0;
/* 2 */
for(; ;)
{
/* 3 */
v = kleinster_unbekannter_Distanzknoten;
/* 4 */
if (v == null)
/* 5 */
break;
/* 6 */
v.bekannt = true;
/* 7 */
for each w benachbart_zu v
/* 8 */
if (!w.bekannt)
/* 9 */
if (v.dist + cvw < w.dist)
{
/* 10 */
w.dist = v.dist + cvw;
/* 11 */
w.pfad = v;
}
}
}
Die Laufzeit des Algorithmus resultiert aus dem Aufsuchen aller Knoten (in den
beiden for−Schleifen) und im Aufsuchen der Kanten (c(vw)) (in der inneren for−
Schleife): O(|E| + |V|2) = O(|V|2).
Implementierung .
21
import java.util.*;
import java.io.*;
class Vertex
{
String
name;
21
// Name des Knoten
vgl.pr22851
40
Algorithmen und Datenstrukturen
LinkedList adj;
// Benachbarte Knoten
boolean
bekannt;
int
dist;
// Kosten
Vertex
path;
// Vorheriger Knoten auf dem kuerzesten Pfad
// Konstruktor
public Vertex(String nm)
{ name = nm; adj = new LinkedList( ); reset( ); }
// Methode
public void reset( )
{ dist = Graph.INFINITY; path = null; bekannt = false; }
}
public class Graph
{
public static final int INFINITY = Integer.MAX_VALUE;
private HashMap vertexMap = new HashMap(); // Abbildung der Knoten
private HashMap edgeMap
= new HashMap(); // Abbildung der Kanten
// Methode Hinzufuegen Kante
public void addEdge(String sourceName,String destName,String distanz)
{
Vertex v = getVertex(sourceName);
Vertex w = getVertex(destName);
String key = sourceName + destName;
v.adj.add(w);
edgeMap.put(key,distanz);
}
// Ausgabe des Pfads
public void printPath(String destName) throws NoSuchElementException
{
Vertex w = (Vertex) vertexMap.get(destName);
if( w == null )
throw new NoSuchElementException( "Destination vertex not found" );
else if( w.dist == INFINITY )
System.out.println( destName + " is unreachable" );
else
{
System.out.println(w.dist);
printPath( w );
System.out.println( );
}
}
// Falls vertexName nicht da ist, fuege den Knoten
// mit diesem Namen in die vertexMap.
// In jedem Fall: Rueckgabe des Knoten.
private Vertex getVertex(String vertexName)
{
Vertex v = (Vertex) vertexMap.get(vertexName);
if( v == null )
{
v = new Vertex(vertexName);
vertexMap.put(vertexName, v);
}
return v;
}
private void printPath(Vertex dest)
{
if( dest.path != null )
{
printPath( dest.path );
System.out.print( " to " );
}
System.out.print( dest.name );
}
private void clearAll( )
{
for( Iterator itr = vertexMap.values( ).iterator( ); itr.hasNext( ); )
( (Vertex)itr.next( ) ).reset( );
}
public void dijkstra(String startName) throws NoSuchElementException
{
clearAll( );
Vertex v, w, u;
Vertex start = (Vertex) vertexMap.get(startName);
if( start == null )
41
Algorithmen und Datenstrukturen
throw new NoSuchElementException( "Startknoten wurde nicht gefunden" );
start.dist = 0;
v = start; w = start; u = start;
for (; ;)
{
if (v == null) break;
v.bekannt = true;
int kleinstW = INFINITY;
for( Iterator itr = v.adj.iterator( ); itr.hasNext( ); )
{
w = (Vertex) itr.next( );
if (w == null) break;
if (!w.bekannt)
{
String key = v.name + w.name;
int cvw
= Integer.parseInt((String) edgeMap.get(key));
if (v.dist + cvw < w.dist)
{
w.dist = v.dist + cvw;
w.path = v;
}
}
}
for( Iterator itr = vertexMap.values( ).iterator( ); itr.hasNext( ); )
{
Vertex x = (Vertex) itr.next( );
if (!x.bekannt && x.dist != INFINITY)
{
if (kleinstW > x.dist)
{
kleinstW = x.dist;
u = x;
}
}
}
if (!u.bekannt) v = u;
else v = null;
}
}
/*
* Verarbeitung einer Anforderung;
* Rueckgabe false, falls Dateiende.
*/
public static boolean processRequest(BufferedReader in, Graph g)
{
String startName = null;
String destName = null;
try
{
System.out.print("Starknoten: ");
if( (startName = in.readLine( ) ) == null )
return false;
System.out.print("Zielknoten: " );
if( (destName = in.readLine( ) ) == null )
return false;
// System.out.println(startName);
g.dijkstra(startName);
System.out.print("Kuerzester Weg: ");
g.printPath(destName);
}
catch( Exception e )
{ System.err.println( e ); }
return true;
}
/*
* Eine main()−Routine, die
* 1. Eine Datei liest, die Kanten enthaelt
*
(Der Dateiname wird als Parameter ueber die
*
Kommandozeile eingegeben);
* 2. den Graphen aufbaut;
* 3. wiederholt 2 Knoten anfordert und
*
den Algorithmus zur Berechnung der kuerzesten Pfade
*
in Gang setzt.
* Die Datei besteht aus Zeilen mit dem Format
42
Algorithmen und Datenstrukturen
*
Quelle (source) Ziel (destination).
*/
public static void main(String [] args)
{
Graph g = new Graph( );
try
{
FileReader din = new FileReader(args[0]);
BufferedReader graphFile = new BufferedReader(din);
// Lies die Kanten und fuege ein
String zeile;
while( ( zeile = graphFile.readLine() ) != null )
{
StringTokenizer st = new StringTokenizer(zeile);
try
{
if( st.countTokens( ) != 3 )
throw new Exception( );
String source = st.nextToken( );
String dest
= st.nextToken( );
String distanz = st.nextToken();
g.addEdge(source, dest, distanz);
}
catch( Exception e )
{ System.err.println( e + " " + zeile ); }
}
}
catch( Exception e )
{ System.err.println( e ); }
System.out.println( "File read" );
BufferedReader in = new BufferedReader(
new InputStreamReader( System.in ) );
while( processRequest( in, g ) )
;
}
}
Ein Problem des vorstehenden Agorithmus ist das Durchsuchen der Knotenmenge
nach der kleinsten Distanz . Man kann das wiederholte Bestimmen der kleinsten
Distanz
einer
prioritätsgesteuerten
Warteschlange
übertragen.
Der
Leistungsaufwand beträgt dann O(|E| log(|V)+|V| log(|V|)). Der Algorithmus (in
Pseudocode) könnte so aussehen:
22
v ∈V do d (v ) = ∞
d ( s) = 0 ; S = 0
/* 2 */
/* 1 */ for_all
/* 3 */ pq = new PriorityQueue(); // Vorrangwarteschlange für Knoten in V
pq ≠ 0 do /* pq = V S */
pq.delete _ min()
/* 5 */
v
/* 6 */ S = S ∪ {}
for _ all( v, w) ∈ E do
/* 7 */
/* 4 */ while
d (v ) + c(v , w) < d ( w) pq.decrease_ key( w, d (v) + c (v, w))
( v, w) aus E
/* 9 */ Entferne
/* 8 */ if
/*10*/ end while
2. Implementierung mit Hilfe einer Schlange
22
v = kleinster_unbekannter_Distanzknoten
43
Algorithmen und Datenstrukturen
Negativ bewertete Kanten. Falls der Graph negativ bewertete Kanten hat,
funktioniert der Algorithmus von Dijkstra nicht. Implementiert man den Dijkstra−
Algorithmus mit einer Schlange, dann dürfen Kantenbewertungen auch negativ sein:
void negativGewichtet(Vertex s)
{
Queue q;
Vertex v, w;
q = new Queue();
q = enqueue(s);
while(!q.isEmpty())
{
v = dequeue();
for each w benachbart_zu w
if (v.dist + cvw < w.dist)
{
w.dist = v.dist + cvw;
w.path = v;
if (w ist_nicht_in q)
q.enqueue(w);
}
}
}
Implementierung.
23
import java.util.*;
import java.io.*;
class Vertex
{
String
name;
// Name des Knoten
LinkedList adj;
// Benachbarte Knoten
boolean
bekannt;
int
dist;
// Kosten
Vertex
path;
// Vorheriger Knoten auf dem kuerzesten Pfad
// Konstruktor
public Vertex(String nm)
{ name = nm; adj = new LinkedList( ); reset( ); }
// Methode
public void reset( )
{ dist = Graph.INFINITY; path = null; bekannt = false; }
}
public class Graph
{
public static final int INFINITY = Integer.MAX_VALUE;
private HashMap vertexMap = new HashMap(); // Abbildung der Knoten
private HashMap edgeMap
= new HashMap(); // Abbildung der Kanten
// Methode Hinzufuegen Kante
public void addEdge(String sourceName,String destName,String distanz)
{
Vertex v = getVertex(sourceName);
Vertex w = getVertex(destName);
v.adj.add(w);
String key = sourceName + destName;
edgeMap.put(key,distanz);
}
// Ausgabe des Pfads
public void printPath(String destName) throws NoSuchElementException
{
Vertex w = (Vertex) vertexMap.get(destName);
if( w == null )
throw new NoSuchElementException( "Zielknoten nicht gefunden" );
else if( w.dist == INFINITY )
System.out.println( destName + " ist nicht erreichbar" );
else
{
printPath( w );
System.out.println(" = " + w.dist);
23
vgl. pr22852
44
Algorithmen und Datenstrukturen
}
}
// Falls vertexName nicht da ist, fuege den Knoten
// mit diesem Namen in die vertexMap.
// In jedem Fall: Rueckgabe des Knoten.
private Vertex getVertex(String vertexName)
{
Vertex v = (Vertex) vertexMap.get(vertexName);
if( v == null )
{
v = new Vertex(vertexName);
vertexMap.put(vertexName, v);
}
return v;
}
private void printPath(Vertex dest)
{
if( dest.path != null )
{
printPath( dest.path );
System.out.print( " to " );
}
System.out.print( dest.name );
}
private void clearAll( )
{
for( Iterator itr = vertexMap.values( ).iterator( ); itr.hasNext( ); )
( (Vertex)itr.next( ) ).reset( );
}
public void negGew(String startName) throws NoSuchElementException
{
clearAll();
Vertex v, w;
LinkedList q = new LinkedList();
Vertex start = (Vertex) vertexMap.get(startName);
if( start == null )
throw new NoSuchElementException( "Startknoten wurde nicht gefunden" );
q.addLast(start); start.dist = 0;
while(!q.isEmpty())
{
v = (Vertex) q.removeFirst();
for( Iterator itr = v.adj.iterator(); itr.hasNext( ); )
{
w = (Vertex) itr.next();
String key = v.name + w.name;
int cvw
= Integer.parseInt((String) edgeMap.get(key));
if ( (v.dist + cvw) < w.dist)
{
w.dist = v.dist + cvw;
w.path = v;
if (!q.contains(w))
q.addLast(w);
}
}
}
}
/*
* Verarbeitung einer Anforderung;
* Rueckgabe false, falls Dateiende.
*/
public static boolean processRequest(BufferedReader in, Graph g)
{
String startName = null;
String destName = null;
try
{
System.out.println( "Starknoten:" );
if( (startName = in.readLine( ) ) == null )
return false;
System.out.println( "Zielknoten:" );
if( (destName = in.readLine( ) ) == null )
return false;
g.negGew(startName);
g.printPath(destName);
45
Algorithmen und Datenstrukturen
}
catch( Exception e )
{ System.err.println( e ); }
return true;
}
/*
* Eine main()−Routine, die
* 1. Eine Datei liest, die Kanten enthaelt
*
(Der Dateiname wird als Parameter ueber die
*
Kommandozeile eingegeben);
* 2. den Graphen aufbaut;
* 3. wiederholt 2 Knoten anfordert und
*
den Algorithmus zur Berechnung der kuerzesten Pfade
*
in Gang setzt.
* Die Datei besteht aus Zeilen mit dem Format
*
Quelle (source) Ziel (destination).
*/
public static void main(String [] args)
{
Graph g = new Graph( );
try
{
FileReader din = new FileReader(args[0]);
BufferedReader graphFile = new BufferedReader(din);
// Lies die Kanten und fuege ein
String zeile;
while( ( zeile = graphFile.readLine() ) != null )
{
StringTokenizer st = new StringTokenizer(zeile);
try
{
if( st.countTokens( ) != 3 )
throw new Exception( );
String source = st.nextToken( );
String dest
= st.nextToken( );
String distanz = st.nextToken();
g.addEdge(source, dest, distanz);
}
catch( Exception e )
{ System.err.println( e + " " + zeile ); }
}
}
catch( Exception e )
{ System.err.println( e ); }
System.out.println( "File read" );
BufferedReader in = new BufferedReader(
new InputStreamReader( System.in ) );
while( processRequest( in, g ) )
;
}
}
3. Implementierung des Algorithmus von Dijkstra nach dem Verfahen von
Bellman/Ford
Negative Kantengewichte können auch im Rahmen des Optimalitätsprinzips von
Bellman zur Lösung des Problems kürzester Wege benutzt werden. Eine
Anwendung des Optimalitätsprinzip auf das "Shortest Path"−Problem zeigt der
Bellman−Ford Algorithmus:
void bellmanford(Vertex s)
{
Vertex v, w;
s.dist = 0;
for I = 1 to
{
for_each
{
E −1
( v, w) ∈ E
46
Algorithmen und Datenstrukturen
if ((v.dist + cvw) < w.dist)
{
w.dist = v.dist + cvw;
}
}
}
}
47
Algorithmen und Datenstrukturen
2.2.8.5.3 Berechnung eines minimal spannenden Baums in einem zusammenhängenden,
ungerichteten, gewichteten Graphen (Algorithmus von Prim)
ein endlicher, zusammenhängender Graph
Gewichtsfunktion g : E → ℜ+ (Gewicht oder Länge der Kante).
Gegeben
ist
G
=
(V,E)
mit
Gesucht ist ein spannender Baum für G.
Defintion: Ein spannender Baum ist ein zusammenhängender, azyklischer Teilgraph
von G, der alle Knoten miteinander verbindet.
Die Kosten von T sind die Summe der Gewichte aller Kanten in T.
Aufgabe. Berechne einen spannenden Baum mit minimalen Kosten (minimum
spanning tree).
Lösungsbeschreibung. Der folgende Graph
2
k1
k2
4
1
3
10
2
7
k3
k4
5
8
k5
4
k6
6
k7
1
besitzt folgenden minimale Spannbaum:
2
k1
k2
1
2
k3
k4
k5
4
6
k6
k7
1
Abb.:
Die Anzahl der Kanten in einem minimal spannenden Baum ist |V| − 1 (Anzahl der
Knoten − 1). Der minimal spannende Baum ist
− ein Baum, der keine Zyklen besitzt.
− spannend, da er jeden Knoten abdeckt.
− ein Minimum.
Der Algorithmus von Prim arbeitet stufenweise. Auf jeder Stufe wird ein Knoten
ausgewählt. Die Kanten auf seine nachfolgenden Knoten werden dann untersucht.
Die Untersuchung folgt nach den Vorschriften des Dijkstra−Algorithmus. Es gibt nur
d = min(d v , c vw )
eine Ausnahme hinsichtlich der Ermittlung der Distanz: w
Die Ausgangssituation zeigt folgende Tabelle:
48
Algorithmen und Datenstrukturen
k
k1
k2
k3
k4
k5
k6
k7
bekannt
false
false
false
false
false
false
false
dv
0
∞
∞
∞
∞
∞
∞
pv
null
null
null
null
null
null
null
Abb.: Ausgangssituation
"k1" wird ausgewählt, "k2, k3, k4 sind zu k1 benachbart". Das führt zur folgenden
Tabelle:
k
k1
k2
k3
k4
k5
k6
k7
bekannt
true
false
false
false
false
false
false
dv
0
2
4
1
∞
∞
∞
pv
null
k1
k1
k1
null
null
null
Abb.: Die Tabelle im Zustand "k1 ist bekannt"
Der nächste Knoten, der ausgewählt wird ist k4. Jeder Knoten ist zu k4 benachbart.
Ausgenommen ist k1, da dieser Knoten "bekannt" ist. k2 bleibt unverändert, denn die
"Kosten" von k4 nach k2 sind 3, bei k2 ist 2 eingetragen. Der Rest wird, wie die
folgende Tabelle zeigt, verändert:
k
k1
k2
k3
k4
k5
k6
k7
bekannt
true
false
false
true
false
false
false
dv
0
2
2
1
7
8
4
pv
null
k1
k4
k1
k4
k4
k4
Abb.: Die Tabelle im Zustand "k4 ist bekannt"
Der nächste Knoten, der ausgewählt wird, ist k2. Das zeigt keine Auswirkungen.
Dann wird k3 gewählt. Das bewirkt eine Veränderung der Distanz zu k6.
k
k1
k2
k3
k4
k5
k6
k7
bekannt
true
true
true
true
false
false
false
dv
0
2
2
1
7
5
4
pv
null
k1
k4
k1
k4
k3
k4
Abb.: Tabelle mit Zustand "k2 ist bekannt" und (anschließend) mit dem Zustand "k3 ist bekannt"
49
Algorithmen und Datenstrukturen
Es folgt die Wahl des Knoten k7, was die Ausrichtung von k6 und k5 bewirkt:
k
k1
k2
k3
k4
k5
k6
k7
Bekannt
true
true
true
true
false
false
true
dv
0
2
2
1
6
1
4
pv
null
k1
k4
k1
k7
k7
k4
Abb.: Tabelle mit Zustand "k7 ist bekannt"
Jetzt werden noch k6 und dann k5 bestimmt. Die Tabelle nimmt danach folgende
Gestalt an:
k
k1
k2
k3
k4
k5
k6
k7
Bekannt
true
true
true
true
true
true
true
dv
0
2
2
1
6
1
4
pv
null
k1
k4
k1
k7
k7
k4
Abb.: Tabelle mit Zustand "k6 ist bekannt" und (anschließend) "k5 ist bekannt"
Die Tabelle zeigt, daß folgende Kanten den minimal spannenden Baum bilden:
(k2,k1),k3,k4)(k4,k1),(k5,k7),(k6,k7),(k7,k4)
Der Algorithmus von Prim zeigt weitgehende Übereinstimmung mit dem Algorithmus
von Dijkstra. Er besitzt aber auch Gültigkeit für ungerichtete Graphen. Jede Kante ist
daher in zwei Adjazenzlisten zu führen. Ohne Heaps ist die Laufzeit O(|V|2).
50
Algorithmen und Datenstrukturen
2.2.8.5.4 Topologisches Sortieren
Sortieren bedeutet Herstellung einer totalen (vollständigen) Ordnung. Es gibt auch
Prozesse zur Herstellung von teilweisen Ordnungen , d.h.: Es gibt eine Ordnung für
einige Paare dieser Elemente, aber nicht für alle. In Graphen für die Netzplantechnik
ist die Feststellung partieller Ordnungen zur Berechnung der kürzesten (und
längsten) Wege erforderlich.
Bsp.: Die folgende Darstellung zeigt einen Netzplan zur Ermittlung des kritischen
Wegs. Die einzelnen Knoten des Graphen sind Anfangs− und Endereignispunkte der
Tätigkeiten, die an den Kanten angegeben sind. Die Kanten (Pfeile) beschreiben die
Vorgangsdauer und sind Abbildungen binärer Relationen. Zwischen den Knoten liegt
eine partielle Ordnungsrelation.
24
Bestelle A
50 Tage
Baue B
1
Teste B
4
20 Tage
Korrigiere Fehler
2
25 Tage
3
15 Tage
Handbucherstellung
60 Tage
Abb. : Ein Graph der Netzplantechnik
Zur Berechnung des kürzesten Wegs sind folgende Teilfolgen, die partiell geordnet
sind, nötig:
1 −> 3:
50 Tage
1−>4−>2−>3: 60 Tage
1−>4−>3:
80 Tage (kürzester Weg)
Eindeutig ist das Bestimmen der topologischen Folgen nicht. Zu dem folgenden
Graphen
2
1
4
3
kann es mehrere topologische Folgen geben.Zwei dieser topologischen Folgen sind
24
vgl. 1.2.2.2
51
Algorithmen und Datenstrukturen
1
2
1
3
3
4
2
4
Abb.:
Bezugspunkt zur Ableitung eines Algorithmus für den topologischen Sort ist ein
gerichteter, azyklischer Graph, z.B.
0
1
2
3
1
2
3
4
1
5
3
6
2
7
Über der Knotenidentifikationen ist zusätzlich die Anzahl der Vorgänger vermerkt. Dieser Zähler wird
in die Knotenbeschreibung aufgenommen. Der Zähler soll festhalten, wie viele unmittelbare Vorgänger
der Knoten hat. Hat ein Knoten keine Vorgänger, dann wird der Zähler auf 0 gesetzt.
Damit kann der Algorithmus durch folgende Pseudocode−Darstellung beschrieben
werden.
void topsort()
{
Queue q;
int zaehler = 0;
Vertex v, w;
q = new Queue();
for each vertex v
if (v.indegree25 == 0)
q = new Queue();
while (!q.isEmpty())
{
v = q.dequeue();
zaehler++;
for each w adjacent to v
if (−−w.indegree == 0)
q.enqueue(w);
}
if (zaehler != anzahlKnoten)
System.out.println("Fehler: Zyklus gefunden");
}
25
indegree ist der Zähler für die jeweilige Anzahl von Vorgängerknoten
52
Algorithmen und Datenstrukturen
Zur Bestimmung der gewünschten topologischen Folge wird mit den
Knotenpunktnummern begonnen, deren Zähler den Wert 0 enthalten. Sie verfügen
über keinen Vorgänger und erscheinen in der topologischen Folge an erster Stelle.
Implementierung :
26
import java.util.*;
import java.io.*;
class Vertex
{
String
name;
// Name des Knoten
LinkedList adj;
// Benachbarte Knoten
int
indegree = 0; // Ingrad des Knoten
// int
dist;
// Kosten
// Vertex
path;
// Vorheriger Knoten auf dem kuerzesten Pfad
// Konstruktor
public Vertex( String nm )
{ name = nm; adj = new LinkedList(); }
}
public class Graph
{
// Abbildung der Knoten
private HashMap vertexMap = new HashMap();
// Methode Hinzufuegen Kante
public void addEdge(String sourceName,String destName)
{
Vertex v = getVertex(sourceName);
Vertex w = getVertex(destName);
w.indegree++;
v.adj.add(w);
}
// Falls vertexName nicht da ist, fuege den Knoten
// mit diesem Namen in die vertexMap.
// In jedem Fall: Rueckgabe des Knoten.
private Vertex getVertex(String vertexName)
{
Vertex v = (Vertex) vertexMap.get(vertexName);
if( v == null )
{
v = new Vertex(vertexName);
vertexMap.put(vertexName, v);
}
return v;
}
/*
* Herstellung der Ordnung von Knoten in einem
* gerichteten, azyklischen Graphen
*/
public void topsort()
{
Vertex v = null, w;
int zaehler = 0;
// Schlange fuer breadth search first
LinkedList q = new LinkedList( );
for (Iterator itr = vertexMap.values().iterator(); itr.hasNext();)
{
v = ((Vertex) itr.next());
if (v.indegree == 0)
{
// enqueue: Einreihen in die Schlange
q.addLast(v);
// System.out.println(v.name);
}
}
if (v == null)
{
System.out.println("Fehler: Kein vorgaengerloser Knoten");
System.exit(0);
26
vgl. pr22854
53
Algorithmen und Datenstrukturen
}
while( !q.isEmpty( ) )
{
// dequeue: Entnehmen aus der Schlange
v = (Vertex) q.removeFirst( );
zaehler++;
System.out.print(v.name + " ");
for( Iterator itr = v.adj.iterator( ); itr.hasNext( ); )
{
w = (Vertex) itr.next( );
if(−−w.indegree == 0)
{
q.addLast( w );
}
}
}
// System.out.println(vertexMap.size());
// System.out.println(zaehler);
if (zaehler != vertexMap.size())
{
System.out.println("Fehler: Zyklus gefunden");
System.exit(0);
}
}
/*
* Eine main()−Routine, die
* 1. Eine Datei liest, die Kanten enthaelt
*
(Der Dateiname wird als Parameter ueber die
*
Kommandozeile eingegeben);
* 2. den Graphen aufbaut;
* 3. wiederholt 2 Knoten anfordert und
*
den Algorithmus zur Berechnung des topologischen Sort
*
in Gang setzt.
* Die Datei besteht aus Zeilen mit dem Format
*
Quelle (source) Ziel (destination).
*/
public static void main(String [] args)
{
Graph g = new Graph( );
try
{
FileReader din = new FileReader(args[0]);
BufferedReader graphFile = new BufferedReader(din);
// Lies die Kanten und fuege ein
String zeile;
while( ( zeile = graphFile.readLine() ) != null )
{
StringTokenizer st = new StringTokenizer(zeile);
try
{
if( st.countTokens( ) != 2 )
throw new Exception( );
String source = st.nextToken( );
String dest
= st.nextToken( );
g.addEdge(source, dest);
}
catch( Exception e )
{ System.err.println( e + " " + zeile ); }
}
}
catch( Exception e )
{ System.err.println( e ); }
System.out.println( "File read" );
// System.out.print(g.vertexMap);
// System.out.println(g.vertexMap.size());
g.topsort();
System.out.println();
}
}
54
Algorithmen und Datenstrukturen
Schreibtischtest. Die folgende Tabelle soll die Veränderung des Zählers für
unmittelbare Vorgänger zeigen und über die Knotenidentifikationen das Ein− bzw.
Ausgliedern aus der Schlange (Queue) q.
Vertex
1
2
3
4
5
6
7
Enqueue
Dequeue
1
0
1
2
3
1
3
2
1
1
2
0
0
1
2
1
3
2
2
2
3
0
0
1
1
0
3
2
5
5
4
0
0
1
0
0
3
1
4
4
5
0
0
0
0
0
2
0
3,7
3
6
0
0
0
0
0
1
0
7
7
0
0
0
0
0
0
0
6
6
Die Tabelle wurde mit den Daten des folgenden, azyklischen Graphen erstellt:
0
1
2
3
1
2
3
4
1
5
3
6
2
7
55
Algorithmen und Datenstrukturen
2.2.9 Algorithmen
Die Wahl einer geeigneten Datenstruktur ist der erste Schritt. Im zweiten Schritt
müssen die Algorithmen implementiert werden. Die Java Bibliothek hilft mit einigen
Standardalgorithmen weiter. Dazu zählen Funktionen zum Sortieren und Suchen in
Containern und das Füllen von Containern. Zum flexiblen Einsatz dieser Funktionen
haben die Java−Entwickler die Klasse Collections bereitgestellt. Collections bietet
Algorithmen statischer Funktionen an, die als Parameter ein Collection Objekt
erwarten. Leider sind viele Algorithmen nur auf List Objekte definiert , z.B.
27
public static void shuffle(List list)
// würfelt die Werte einer Liste durcheinander
Bsp.28:
import java.util.*;
public class VectorShuffle
{
public static void main(String args[])
{
Vector v = new Vector();
for (int i = 0; i < 10; i++)
v.add(new Integer(i));
Collections.shuffle(v);
System.out.println(v);
}
}
public static void shuffle(List list, random rnd)
// würfelt die werte der Liste durcheinander und benutzt dabei den Random Generator rnd.
Nur die Methoden min() und max() arbeiten auf allgemeinen Collection−Objekten.
2.2.9.1 Datenmanipulation
Daten umdrehen. Die Methode reverse() dreht die Werte einer Liste um. Die
Laufzeit ist linear zu der Anzahl der Elemente.
public static void reverse(List l)
// dreht die Elemente in der Liste um
Listen füllen. Mit der fill()−Methode läßt sich eine Liste in linearer Zeit belegen.
Nützlich ist dies, wenn eine Liste mit Werten initialisiert werden muß.
public static void fill (List l, Object o)
// füllt eine Liste mit dem Element o
Daten zwischen Listen kopieren. Die Methode copy(List quelle, List ziel)
kopiert alle Elemente von quelle in die Liste ziel und überschreibt dabei
Elemente, die evtl. an dieser Stelle liegen.
public static void copy(List quelle, List ziel)
// kopiert Elemente von quelle nach ziel. Ist ziel zu klein, gibt es eine IndexOutOfBoundsException
27
28
Nutzt die Collection Klasse keine List Objekte, arbeitet sie mit Iterator Objekten, um allgemein zu bleiben
vgl. pr22122
56
Algorithmen und Datenstrukturen
2.2.9.2 Größter und kleinster Wert einer Collection
Die Methoden min() und max() suchen das größte und kleinste Element einer
Collection. Die Laufzeit ist linear zur Größe der Collection. Die Methoden machen
keinen Unterschied, ob die Liste schon sortiert ist oder nicht.
public static Object min(Collection c)
//
public static Object max(Collection c)
/* Falls min() bzw. max() auf ein Collection−Objekt angewendet wird, erfolgt die Bestimmung des
Minimums bzw. Maximums nach der Methode compareTo() der Comparable Schnittstelle. Byte,
Character, Double, File, Float, Long, Short, String, Integer, BigInteger, ObjectStreamField, Date und
Calendar haben diese Schnittstelle implementiert. Lassen sich die Daten nicht vergleichen, dann gibt
es eine ClassCastException.
*/
public static Object min(Collection c, Comparator vergl)
//
public static Object max(Collection c, Comparator vergl)
2.2.9.3 Sortieren
Die Collection Klasse bietet zwei sort() Methoden an, die die Elemente einer Liste
stabil sortieren. Die Methode sort() sortiert die Elemente in ihrer natürlichen
Ordnung, z.B.:
29
− Zahlen nach der Größe (13 < 40)
− Zeichenketten alphanumerisch (Juergen < Robert < Ulli)
Eine zweite überladene Form von sort() arbeitet mit einem speziellen Comparator
Objekt, das zwei Objekte mit der Methode compare() vergleicht.
public static void sort(List liste)
// sortiert die Liste
public static void sort(List liste,Comparator c)
// sortiert die Liste mit dem Comparator c
Die Sortierfunktion arbeitet nur mit List−Objekten. "sort()" gibt es aber auch in der
Klasse Arrays.
Bsp.: Das folgende Programm sortiert eine Reihe von Zeichenketten in
aufsteigender Folge. Es nutzt die Methode Arrays.asList() zur Konstruktion
einer Liste aus einem Array .
30
import java.util.*;
public class CollectionsSortDemo
{
public static void main(String args[])
{
String feld[] =
{ "Regina","Angela","Michaela","Maria","Josepha",
"Amalia","Vera","Valentina","Daniela","Saida",
"Linda","Elisa"
};
List l = Arrays.asList(feld);
Collections.sort(l);
29
Stabile Sortieralgorithmen beachten die Reihenfolge von gleichen Elementen, z.B. beim Sortieren von
Nachrichten in einem Email−Programm, zuerst nach dem Datum und anschließend nach dem Sender, soll die
Liste innerhalb des Datum sortiert bleiben.
30 Leider gibt es keinen Konstruktor für ArrayList, der einen Array mit Zeichenketten zuläßt.
57
Algorithmen und Datenstrukturen
System.out.println(l);
}
}
Die Java Bibliothek bietet nicht viel zur Umwandlung von Feldern ("Array") in
dynamische Datenstrukturen. Eine Ausnahme bildet die Hilfsklasse Arrays, die die
Methode asList() anbietet. Die Behälterklassen ArrayList und LinkedList
werden über asList() nicht unterstützt, d.h. Über asList() wird zwar eine
interne Klasse ArrayList benutzt, die eine Erweiterung von AbstractList ist,
aber nur das notwendigste implementiert.
Sortieralgorithmus. Es handelt sich um einen optimierten "Merge−Sort". Seine
Laufzeit beträgt N ⋅ log(N ) .
Die sort() Methode arbeitet mit der toArray() Funktion der Klasse List. Damit
werden die Elemente der Liste in einem Feld (Array) abgelegt. Schließlich wird die
sort() Methode der Klasse Arrays genutzt und mit einem ListIterator wieder
in die Liste eingefügt.
Daten in umgekehrter Reihenfolge sortieren. Das wird über ein spezielles
Comparator−Objekt geregelt, das von Collections über die Methode
reverseOrder() angefordert werden kann.
Bsp. :
31
import java.util.*;
public class CollectionsReverseSortDemo
{
public static void main(String args[])
{
Vector v = new Vector();
for (int i = 0; i < 10; i++)
{
v.add(new Double(Math.random()));
}
Comparator comparator = Collections.reverseOrder();
Collections.sort(v,comparator);
System.out.println(v);
}
}
Eine andere Möglichkeit für umgekehrt sortierte Listen besteht darin, erst die Liste
mit sort() zu sortieren und anschließend mit reverse() umzudrehen.
31
Vgl. pr22122
58
Algorithmen und Datenstrukturen
2.2.9.4 Suchen von Elementen
Die Behälterklassen enthalten die Methode contains(), mit der sich Elemente
suchen lassen. Für sortierte Listen gibt es eine wesentlich schnellere Suchmethode:
binarySearch():
public static int binarySearch(List liste, Object key)
// sucht ein Element in der Liste. Gibt die Position zurück oder ein Wert kleiner 0,
// falls key nicht in der Liste ist.
public static int binarySearch(List liste, Object key, Comparator c)
// Sucht ein Element mit Hilfe des Comparator Objekts in der Liste. Gibt die Position zurück oder
// einen Wert kleiner als 0, falls der key nicht in der Liste ist.
Bsp. : Das folgende Programm sortiert (zufällig ermittelte) Daten und bestimmt
Daten in Listen mit Hilfe der binären Suche.
32
import java.util.*;
public class ListSort
{
public static void main(String [] args)
{
final int GR = 20;
// Verwenden einer natuerliche Ordnung
List a = new ArrayList();
for (int i = 0; i < GR; i++)
a.add(new VglClass((int)(Math.random() * 100)));
Collections.sort(a);
Object finde = a.get(GR / 2);
int ort = Collections.binarySearch(a,finde);
System.out.println("Ort von " + finde + " = " + ort);
// Verwenden eines Comparator
List b = new ArrayList();
// Bestimmt zufaellig Zeichenketten der Laenge 4
for (int i = 0; i < GR; i++)
b.add(Felder.randString(4));
// Instanz fuer den Comparator
AlphaVgl av = new AlphaVgl();
// Sortieren
Collections.sort(b,av);
// Binaere Suche
finde = b.get(GR / 2);
ort = Collections.binarySearch(b,finde,av);
System.out.println(b);
System.out.println("Ort von " + finde + " = " + ort);
}
}
2.2.9.5 Typsichere Datenstrukturen
Die Datenstrukturen des Pakets java.util haben einen großen Nachteil: Die
eingesetzten typen sind immer vom Typ Object. Typsicherheit über Templates, wie
C++ es bietet, ist bisher nicht vorgesehen. Es spricht einiges dafür, daß in den
nächsten Javagenerationen generische Typen Berücksichtigung finden.
32
Vgl. pr22122
59