Experimentelle Methoden Atomphysik
Werbung

Vorlesung an der Universität Heidelberg im Wintersemester 2001/02 Experimentelle Methoden der Atomphysik Gerald Gwinner Max-Planck-Institut für Kernphysik Note: this document is best viewed with Acrobat 5 or higher, with antialiasing of fonts,line art, and images and “cooltype” enabled (Preferences — Display menu). Inhaltsverzeichnis 1 . . . . . 1 1 5 7 8 12 2 Nachweis von Atomen 2.1 Zähler für geladene Teilchen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2.2 Ionisation von Atomen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 13 17 3 Optische Spektroskopie 3.1 Allgemeines . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3.2 Wechselwirkung zwischen Atom und Strahlung . . . . . . . . . 3.3 Linienbreiten . . . . . . . . . . . . . . . . . . . . . . . . . . . 3.3.1 Verbreiterungsmechanismen . . . . . . . . . . . . . . . 3.3.2 Sättigung und Sättigungsverbreiterung . . . . . . . . . . 3.4 Laserspektroskopische Methoden . . . . . . . . . . . . . . . . . 3.4.1 Frequenzmodulation und phasenempfindliche Detektion 3.4.2 Laserinduzierte Fluoreszenz . . . . . . . . . . . . . . . 3.4.3 Photoakustische Spektroskopie . . . . . . . . . . . . . . 3.5 Nichtlineare Methoden zur dopplerfreien Spektroskopie . . . . . 3.5.1 Sättigungsspektroskopie . . . . . . . . . . . . . . . . . 3.5.2 Zweiphotonenspektroskopie . . . . . . . . . . . . . . . . . . . . . . . . . . . 24 24 24 29 31 34 37 38 39 44 45 45 50 . . . . . . 56 56 56 60 62 63 63 . . . . . . . 70 70 71 72 77 79 79 82 . . . . . 93 93 93 94 98 101 4 5 6 Atom- und Molekularstrahlquellen 1.1 Effusive Quellen . . . . . . . . . . . . . . . . . . . . . . . 1.2 Adiabatische Strahlexpansion durch eine Düse . . . . . . . . 1.3 Quellen für dissoziierte Atome . . . . . . . . . . . . . . . . 1.4 Umladung von Ionenstrahlen . . . . . . . . . . . . . . . . . 1.5 Elektronenablösung (Photodetachment) von negativen Ionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Hochfrequenzspektroskopie 4.1 Allgemeines . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4.2 Magnetische Dipolübergänge . . . . . . . . . . . . . . . . . . . . . 4.3 Übergänge im Zweiniveausystem, quantenmechanische Behandlung 4.4 Bestimmung von Kernmomenten mit dem Rabischen Apparat . . . 4.5 Methode der separierten oszillierenden Felder . . . . . . . . . . . . 4.6 Messungen der Hyperfeinstruktur, Prinzip der Atomuhr . . . . . . . Fallen und Kühlung für neutrale Atome 5.1 Einführung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5.2 Formale Probleme bei der Fallenkonstruktion . . . . . . . . . . . . 5.3 Der Weg zur magneto-optischen Falle, Laserkühlung . . . . . . . . 5.4 Einige technische Details zur MOT . . . . . . . . . . . . . . . . . . 5.5 Weitere Fallen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5.6 Optische Dipolfallen . . . . . . . . . . . . . . . . . . . . . . . . . 5.7 Anwendung von Fallen am Beispiel der Bose-Einstein-Kondensation Atomphysik mit geladenen Teilchen 6.1 Erzeugung von Elektronen-, Positronen- und Ionenstrahlen 6.1.1 Elektronen . . . . . . . . . . . . . . . . . . . . . 6.1.2 Positronen . . . . . . . . . . . . . . . . . . . . . 6.1.3 Ionenquellen . . . . . . . . . . . . . . . . . . . . 6.2 Ionenfallen . . . . . . . . . . . . . . . . . . . . . . . . . i . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6.2.1 6.2.2 6.2.3 6.2.4 6.2.5 Kingdonfalle (1923) . . . . RF-Ionenfalle oder Paulfalle Penningfalle . . . . . . . . Kühlung in Ionenfallen . . . Experimente in Ionenfallen . . . . . . . . . . . ii . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101 101 106 109 113 Abbildungsverzeichnis 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 Abstrahlungscharakteristik einer dünnen Apertur . . . . . . Beispiel einer effusiven Atomstrahlquelle . . . . . . . . . . Vorwärtsbündelung eines Atomstrahls . . . . . . . . . . . . Prinzip der adiabatischen Strahlexpansion . . . . . . . . . . Abkühlung des Strahls mit zunehmender Geschwindigkeit . Hochfrequenzentladungsquelle . . . . . . . . . . . . . . . . Termschema von Helium . . . . . . . . . . . . . . . . . . . Langmuirsches Raumladungsgesetz . . . . . . . . . . . . . Raumladungsbegrenzte Ionenstrahlströme . . . . . . . . . . Geschwindigkeitskomprimierung durch Beschleunigung . . Aufbau für kollineare Spektroskopie . . . . . . . . . . . . . Photodetachment . . . . . . . . . . . . . . . . . . . . . . . LAMPF meson facility, Los Alamos. . . . . . . . . . . . . . Wasserstoffspektrum . . . . . . . . . . . . . . . . . . . . . Das Experiment von L AMB und R ETHERFORD . . . . . . . Prinzip des Elektronenvervielfachers . . . . . . . . . . . . . Prinzip des Channeltrons . . . . . . . . . . . . . . . . . . . Microchannelplates . . . . . . . . . . . . . . . . . . . . . . Ionisationsenergien und Austrittsarbeiten . . . . . . . . . . Atom im externen Feld . . . . . . . . . . . . . . . . . . . . Vergleich zwischen ‘normalen’ und Rydbergatomen . . . . . Parameter für Feldionisation . . . . . . . . . . . . . . . . . Modifikation der spontanen Lebensdauer in einem Resonator Messung zur Modifikation der spontanen Emission . . . . . Elektromagnetisches Spektrum . . . . . . . . . . . . . . . . Beam-foil Spektroskopie . . . . . . . . . . . . . . . . . . . Zweiniveauatom mit Strahlungsprozessen . . . . . . . . . . Suche nach EDM . . . . . . . . . . . . . . . . . . . . . . . Oszillierendes elektrisches Übergangsdipolmoment . . . . . Linienverschiebung bei Kollisionen im Gas . . . . . . . . . Durchflugsverbreiterung. . . . . . . . . . . . . . . . . . . . Voigtprofil . . . . . . . . . . . . . . . . . . . . . . . . . . . Frequenzbereich abstimmbarer Laser . . . . . . . . . . . . . Absorptionsspektroskopie . . . . . . . . . . . . . . . . . . . Prinzip des ‘noise-eaters’ . . . . . . . . . . . . . . . . . . . Ein- und Ausgangssignal der Intensitätsstabilisierung . . . . Ableitungen einer Resonanz . . . . . . . . . . . . . . . . . Lock-in-Verstärker . . . . . . . . . . . . . . . . . . . . . . Yb-Spektroskopie . . . . . . . . . . . . . . . . . . . . . . . Yb-Spektroskopie 2 . . . . . . . . . . . . . . . . . . . . . . Yb-Spektroskopie 3 . . . . . . . . . . . . . . . . . . . . . . Yb-Spektroskopie 4 . . . . . . . . . . . . . . . . . . . . . . Yb-Spektroskopie 5 . . . . . . . . . . . . . . . . . . . . . . Photoakustische Spektroskopie . . . . . . . . . . . . . . . . Prinzip der Sättigungsspektroskopie . . . . . . . . . . . . . Aufbau zur Sättigungsspektroskopie . . . . . . . . . . . . . Sättigung in Rb . . . . . . . . . . . . . . . . . . . . . . . . iii . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 4 5 6 6 7 8 9 10 11 11 12 13 14 14 15 16 16 17 21 22 22 23 23 25 25 26 27 28 31 32 33 37 37 38 39 40 41 41 42 42 43 43 44 45 46 46 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 Rb Termschema . . . . . . . . . . . . Sättigung in Rb . . . . . . . . . . . . Jodspektroskopie, Aufbau . . . . . . . Jodspektrum . . . . . . . . . . . . . . Zweiphotonenübergänge, Schema . . Zweiphotonenspektroskopie . . . . . Genauigkeit der 1s → 2s Frequenz . . 1s → 2s Aufbau . . . . . . . . . . . Temperatur und Linienform . . . . . . Spektroskopie an langsamen Atomen . Vergleich 1s → 2s zu 2s → 4s (I) . . Vergleich 1s → 2s zu 2s → 4s (II) . . Effektive Magnetfeld . . . . . . . . . Rabioszillation 1 . . . . . . . . . . . Rabioszillation 2 . . . . . . . . . . . Linienform . . . . . . . . . . . . . . Rabische Apparatur . . . . . . . . . . Ramseysche Apparatur . . . . . . . . Ramsey-Resonanz 1 . . . . . . . . . . Ramsey-Resonanz 2 . . . . . . . . . . Ramsey-Interferometer . . . . . . . . Breit-Rabi-Formel . . . . . . . . . . . Atomuhr 1 . . . . . . . . . . . . . . . Atomuhr 2 . . . . . . . . . . . . . . . Atomuhr 3 . . . . . . . . . . . . . . . Atomuhr 4 . . . . . . . . . . . . . . . Wasserstoffmaser . . . . . . . . . . . Spontane Lichtkraft . . . . . . . . . . Magnetische Falle . . . . . . . . . . . Dopplerkühlung . . . . . . . . . . . . Optische Melasse . . . . . . . . . . . MOT 1D . . . . . . . . . . . . . . . . Kühlkraft . . . . . . . . . . . . . . . Einfangeffizienz der MOT . . . . . . NIST MOT . . . . . . . . . . . . . . Rückpumplaser . . . . . . . . . . . . Zeeman-Slower . . . . . . . . . . . . Optische Dipolfalle I . . . . . . . . . Optische Dipolfalle II . . . . . . . . . Anwendung in der Biologie . . . . . Pyramidenfalle . . . . . . . . . . . . GOST-Falle . . . . . . . . . . . . . . BEC, Prinzip . . . . . . . . . . . . . BEC Phasenraum . . . . . . . . . . . Evaporatives Kühlen I . . . . . . . . . Evaporatives Kühlen II . . . . . . . . Optischer Propf . . . . . . . . . . . . Kleeblattfalle I . . . . . . . . . . . . Kleeblattfalle II . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . iv . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47 47 48 49 50 51 52 52 53 54 54 55 58 59 60 62 62 64 64 65 65 66 67 67 68 69 69 70 72 73 73 74 76 76 77 78 78 79 80 81 83 83 84 84 85 85 86 87 87 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 Phasenraumdichte . . . . . . . . . . . . . Entstehung eines Kondensats . . . . . . . Phasenkontrastmethode . . . . . . . . . . Interferenz zweier Kondensate . . . . . . Entwicklung der BEC Forschung . . . . . Gepulster Atomlaser . . . . . . . . . . . Kontinuierlicher Atomlaser . . . . . . . . Fermidruck . . . . . . . . . . . . . . . . Mikrofalle . . . . . . . . . . . . . . . . . Elektronenkanone . . . . . . . . . . . . . Positronenproduktion mit Beschleunigern Positronenmoderation . . . . . . . . . . . Lebensdauer von Orthopositronium . . . Produktion von Ps− . . . . . . . . . . . . Annihilationsspektrum von Ps− . . . . . . Ps− am MPIK . . . . . . . . . . . . . . . Einfache Ionenquelle . . . . . . . . . . . Duoplasmatronquelle . . . . . . . . . . . EZR Quelle . . . . . . . . . . . . . . . . EBIS Quelle . . . . . . . . . . . . . . . . 2D Quadrupol . . . . . . . . . . . . . . . Mathieusche DGl.: Stabilität I . . . . . . Mathieusche DGl.: Stabilität II . . . . . . Hyperbolische Paulfalle . . . . . . . . . . Hyperbolische Paulfalle . . . . . . . . . . Stabilität in der 3-dim. Paulfalle. . . . . . Makroskopische Teilchen in der Paulfalle. Mechanisches Modell der Paulfalle. . . . Lithographische Falle I . . . . . . . . . . Lithographische Falle II . . . . . . . . . . Penningfalle. . . . . . . . . . . . . . . . Penningfalle II. . . . . . . . . . . . . . . Widerstandskühlung . . . . . . . . . . . Laserkühlung für langsame Ionen . . . . Laserkühlung für schnelle Ionen . . . . . Ionensorten für Laserkühlung . . . . . . . Geonium . . . . . . . . . . . . . . . . . Leveldiagramm von Hg . . . . . . . . . . Quantensprünge . . . . . . . . . . . . . . Ionenkristall I . . . . . . . . . . . . . . . Ionenkristall II . . . . . . . . . . . . . . Ionenkristall III . . . . . . . . . . . . . . Ionenkristall IV . . . . . . . . . . . . . . Antiprotonen . . . . . . . . . . . . . . . v . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88 88 89 89 90 91 91 92 92 93 94 95 96 96 97 97 98 99 99 100 102 103 104 104 105 106 107 108 108 109 109 110 111 111 112 112 114 114 115 115 115 116 116 117 . vi 1 Atom- und Molekularstrahlquellen Für die Arbeit mit Atomen und Molekülen im freien Raum sind geeignete Strahlquellen notwendig. In einzelnen Fällen kann z.B. ein Gas direkt in einer passenden Zelle, in die es permanent eingefüllt ist, spektroskopiert werden (vor allem Edelgase); man hat dann jedoch wenig Kontrolle über die Stöße der Teilchen untereinander und mit der Zellenwand. Deshalb verwendet man im überwiegenden Teil der Experimente einen Atom- bzw. Molekülstrahl, der nach dem Verlassen der Quellkammer (“Ofen”) praktisch keine Wechselwirkung mit externer Materie hat und auch wenig strahlinterne Kollisionen aufweist. Unter einer Vielzahl von Methoden sind vor allem folgende Techniken relevant: • effusive Quellen • Düsenstrahlmethoden • Dissoziationsquellen • umgeladene Ionenstrahlen 1.1 Effusive Quellen D UNOYER, 1911 (Comptes Rendus 152, 594). Effusiver Fluß: Stöße zwischen den Teilchen sind zu vernachlässigen. Λ: mittlere freie Weglänge d: Durchmesser der Quellöffnung ΛQuelle d Stoßrate R: R = vrel σn Λ = v/R v = vrel σn 1 = √ 2σn v: mittlere Geschwindigkeit eines Teilchens vrel : mittlere relative Geschwindigkeit zwischen √ 2 Teilchen im Gas = 2v σ: Stoßquerschnitt n: Teilchendichte Der gaskinetische Wirkungsquerschnitt σ entspricht in der Größenordnung der Fläche der klassischen Elektronenbahn: σ ≈ πa20 = 10−16 cm2 a0 : Bohrscher Radius 1 Anmerkung: der Wirkungsquerschnitt (engl. cross section) ist eine nützliche und viel benutzte Größe in Streuexperimenten, d.h. Anordnungen mit einem Projektilstrahl, der auf ein sog. Target trifft. Der Wirkungsquerschnitt σ ist definiert durch Anzahl der Reaktionen = Fluß von Projektilteilchen × σ Sekunde × Targetteilchen Der Ausdruck auf der linken Seite entspricht gerade der vom Experimentator beobachteten Rate pro Targetatom. Der Fluß Φ von Projektilteilchen, d.h. die Zahl der Teilchen die pro Zeiteinheit durch eine Einheitsfläche senkrecht zur Strahlrichtung gehen, errechnet sich zu Φ = nProjektil × vProjektil. Der Wirkungsquerschnitt gibt also die Reaktionsrate pro Targetteilchen und pro Einheitsfluß einfallender Teilchen und hat die Dimension einer Fläche (typischerweise cm2 ). Beispiel für die freie mittlere Weglänge Λ: Ideales Gas bei T = 800 K: p = 1 mbar → Λ = 8mm p = 10−3 mbar → Λ = 8m Der Druck in der Quelle sollte so hoch sein wie die Bedingung der Effusivität erlaubt, um den Teilchenfluß im Experiment zu maximieren. Für typische Öffnungen (≈ 1 mm) ist dies im mbar-Bereich. Außerhalb der Öffnung muß der Druck im Vakuumgefäß dann auf mindestens 10−3 mbar abfallen. Austretender Strahl dN dt = n0 f (v) dN/dt: Anzahl austretender Moleküle pro Zeiteinheit n0 : Dichte in der Quelle f (v): Geschwindigkeitsverteilung in der Quelle (Maxwell) dΩ: Raumwinkelelement v: Geschwindigkeit des austretenden Teilchens θ: Winkel zur Öffnungsnormalen S: Öffnungsfläche dv: Breite der beobachteten Geschwindigkeitsgruppe dΩ v cos θ S dv 4π Mit der Definition ṽ = v/vw , wobei vw = Maxwell-Boltzmann-Verteilung ist, folgt: q 2kT /m die wahrscheinlichste Geschwindigkeit in der 4 2 f (ṽ)dṽ = √ ṽ 2 e−ṽ dṽ, π und somit dN n0 S 2 (θ, ṽ) = 3/2 vw ṽ 3 e−ṽ dṽ cos θ dΩ dt π 2 Abbildung 1: Abstrahlungscharakteristik einer dünnen Apertur und eines Kanals mit L = d. Quelle: Ramsey, S. 13. Die Geschwindigkeitsverteilung in einem Strahl skaliert mit v 3 : fStrahl (ṽ) = 2 ṽ 3 e−ṽ Wahrscheinlichste Geschwindigkeit im Strahl: vwB = √ Mittlere Geschwindigkeit: v̄B = 3/4 π vw . 2 q 3/2 vw . Integration über alle Geschwindigkeiten: √ v̄ = (2/ π) vw ≈ 1.13vw : mittlere Geschwindigkeit im Quellgas n0 v̄ dΩ S cos θ I(θ)dΩ = 4 π Die Gesamtrate von Molekülen, die die Öffnung verlassen ist also no v̄S/4, und die Winkelverteilung folgt einem Cosinusgesetz analog dem Lambertschen Gesetz in der Optik. Intensität in Vorwärtsrichtung (θ = 0): n0 v̄S (Atome pro sr und sec) 4π p0 S = 8.55 × 1021 √ MT I(0) = p0 : Quellendruck in mbar S: Quellenöffnung in cm2 M : Molekulargewicht (amu) T : Temperatur in K Die Bedingung d ≈ Λ führt dazu, daß man für eine typische Apertur d = 1 mm für alle Gase einen ähnlichen Standardstrahl mit I(0) ≈ 5 × 1016 (sr sec)−1 erhält. Formel für die Geschwindigkeit von Atomen: 3 Abbildung 2: Beispiel einer effusiven Atomstrahlquelle, hier für die Produktion von atomarem Li. Quelle: U. Schünemann, Diplomarbeit Max-Planck-Inst. für Kernphysik, Heidelberg 1994 vw = 127 m/s s T : Temperatur des Gases in K M : Molekulargewicht T M Erhöhung des Flusses in Vorwärtsrichtung durch Kanäle Bedingung des stoßfreien Durchgangs durch den Kanal: KnL = K: K NUDSEN-Zahl L: Länge des Kanals Λ 1 L L/d → 0 : L/d 1 : I = n0 v̄ S/4 IKanal = W I mit W = 4d/3L Ein langer Kanal erhöht die Intensität in Vorwärtsrichtung relativ zur Gesamtrate und reduziert damit die erforderliche Vakuumpumpleistung: IKanal (0) L ∝ . IKanal d Dieser Aspekt ist besonders wichtig bei Verwendung von seltenen Spezies (z.B. radioaktiven Isotopen): das verfügbare Material wird effektiver ins Experiment gestrahlt (und z.B. die Kontamination der Vakuumkammer minimiert). 4 Abbildung 3: Vorwärtsbündelung eines Atomstrahls für verschiedene Kanallängen und KnudsenZahlen. Quelle: Scoles Band I, S. 89. Problem: Pumpleistung in lange Kanäle begrenzt, schlechtes Vakuum limitiert Λ. Hohe Direktionalität und hoher Fluß können durch den Einsatz einer Matrix von parallelen Kanälen erreicht werden. Dafür bieten sich sog. microchannel plates an, die auch als Teilchendetektor eine wichtige Rolle spielen (siehe unten). 1.2 Adiabatische Strahlexpansion durch eine Düse Gas strömt unter hohem Druck aus einer Düse (mit Durchmesser d) aus mit der Bedingung Λ d. Findet kein Wärmeaustausch mit der Umgebung statt, führt dies zu einer adiabatischen Strahlexpansion hinter der Düse. Ungerichtete thermische Bewegung wird in gerichtete Bewegung umgewandelt. Die Enthalpie des Gases bleibt bei der Expansion unverändert: U0 + p0 V0 + 1/2M u20 = U + pV + 1/2M u2 vor der Expansion: u0 = 0 nach der Expansion: p ≈ 0 → U0 + p0 V0 = U + 1/2M u2 U = Utrans + Urot + Uvib : innere Energie des Gases pV : Kompressionsenergie 1/2M u2 : Strömungsenergie Daraus folgt, daß mit zunehmender Geschwindigkeit u die innere Energie des Gases abnimmt. Neben der Translation kann auch die interne Rotationsenergie von Molekülen gekühlt werden. Abkühlung führt im Extremfall zur Kondensation im Strahl. Dieser Effekt ist bei Messungen an Atomen unerwünscht und wird verhindert durch Verwendung eines seeded beam: 5 Abbildung 4: Prinzip der adiabatischen Strahlexpansion. Quelle: Bergmann-Schäfer, Bd. 4, S. 181. Abbildung 5: Abkühlung des Strahls mit zunehmender Geschwindigkeit. Quelle: Bergmann-Schäfer, Bd. 4, S. 182. 6 Abbildung 6: Beispiel für eine Hochfrequenzentladungsquelle, Toennies et al., Göttingen. Quelle: Scoles, Band I, S. 108. das zu messende Atom/Molekül wird verdünnt in einem He- (oder Ar) Strahl expandiert; damit kann die Kondensation vermieden oder eingestellt werden. Die Kondensation ist für die Clusterphysik sehr nützlich. Aufgrund des hohen Drucks vor der Düse produziert die Expansion einen hohen Hintergrundgasdruck in der Vakuumkammer. Deshalb werden häufig gepulste Jets verwendet. 1.3 Quellen für dissoziierte Atome Viele Gase liegen ursprünglich als Molekül vor, z.B. H2 . Gerade atomarer Wasserstoff ist in der Spektroskopie sehr bedeutend. Dissoziation der Gasmoleküle in der Quelle: • thermische Dissoziation: hohe Temperaturen im Ofen notwendig (Wasserstoff: > 2500 K). • Gasentladung über Elektroden direkt im Quellgas: sehr empfindlich gegen Verunreinigung. • Hochfrequenz-/Mikrowellenentladung: beste Methode, Hochfrequenz wird extern angelegt. 7 Abbildung 7: Termschema von Helium. Quelle: Haken und Wolf. Herstellung metastabiler Atome Hochfrequenzquellen können auch zur Produktion metastabiler Atomstrahlen verwendet werden (z.B. He∗ oder Ne∗ ). Metastabile Zustände eines Atoms/Moleküls können sich nicht durch spontane Emission von Licht in den Grundzustand abregen, da der Zerfall Auswahlregeln für elektrische Dipolstrahlung verletzen würde (z.B. ∆L = 0 oder ∆S = 1 Übergänge). Prominente Beispiele sind Wasserstoff im 2s1/2 Zustand (siehe Versuch von L AMB und R ETHERFORD) und Orthohelium (siehe Abbildung 7). In der Hochfrequenzentladung können Atome durch Stoßanregung in einen metastabilen Zustand gehoben werden. 1.4 Umladung von Ionenstrahlen Die kinetische Energie von thermisch erzeugten Atomen beträgt maximal nur einige zehntel eV. Viele interessante Phänomene spielen sich bei höherer Energie ab. Zwischen 1 und 20 eV: • Chemie: Dissoziationsenergien chemischer Bindungen und Aktivierungsenergien • Ionisationsschwellen • Geschwindigkeit von Satelliten etc. in der oberen Atmosphäre Bei noch höheren Energien: • Atomare Stöße: Untersuchung der kurzreichweitigen, abstoßenden Komponente des Streupotentials 8 • Elektronische Anregungen, Ionisation, Anregung innerer Schalen Plasmaphysik: • Zum Heizen des Plasmas werden energetische Teilchen eingeschossen. Bei magnetischem Einschluß (‘confinement’) ist es vorteilhaft, neutrale Teilchen einzuschießen, die ionisiert werden und erst dann dem Einschluß unterliegen (es wurden z.B. neutrale Strahlen mit 100 A bei bis zu 100 keV Energie realisiert). Ionenstrahlen können sehr leicht beschleunigt werden. Schnelle, einfach geladene Ionen werden dann in einer ‘charge exchange cell’ in einen neutralen Strahl umgeladen. Die Intensität des Ionenstrahls folgt dem Langmuirsches Raumladungsgesetz: j: Stromdichte c: Quellenabhängige Proportionalitätskonstante U : Abzugsspannung M : Molekulargewicht √ j = c U 3/2 / M Abbildung 8: Herleitung des Langmuirschen Raumladungsgesetzes: Auszug aus The Effect of Space Charge and Residual Gases on Thermionic Currents in High Vacuum, I. Langmuir, Phys. Rev. 2, 450-486 (1913). Im Schritt von (7) nach (8) wird partielle Integration mit u(x) = v(x) = dV /dx verwendet. √ Empirisch: j = 2 × 109 × U 3/2 / M Teilchen pro cm2 und sec (siehe Abb. 9). Clou der Umladungszelle: der Umladequerschnitt ist wesentlich größer (≈ 10−14 − 10−15 cm2 ) als der kinetische Stoßquerschnitt (≈ 10−16 cm2 ). Deshalb findet Ladungsaustausch durch periphere Stöße statt, und die Strahlqualität wird kaum beeinflußt. 9 Abbildung 9: Raumladungsbegrenzte Ionenstrahlströme in Abhängigkeit von der Energie. Quelle: Scoles Bd. 1, Seite 128. Kollineare Spektroskopie an schnellen neutralen Atomen Dem Teilchenstrahl wird ein Laserstrahl kollinear überlagert (Abb. 11). Warum verzichtet man nicht auf Umladung und spektroskopiert Ionen? Die Valenzelektronen sind in Ionen stärker gebunden, und deshalb gibt es im Sichtbaren und nahen IR, wo exzellente durchstimmbare Laser existieren, nur wenige geeignete Spektrallinien für Ionen. Kollineare Spektroskopie ist eine Sub-Dopplermethode: E = 1 2 mv 2 dE = mv dv δE = mv δv δE δv = mv Ein Teilchenensemble mit Energiebreite δE wird (z.B. elektrostatisch) auf Energie E beschleunigt. Das Ensemble hat dann immer noch die Energieunschärfe δE (siehe Abb. 10). Aber die Geschwindigkeitsunschärfe δv ist verringert. 10 E=1/2mv2 E δE Beschleunigung um E=eU δE δv2 δv1 v Abbildung 10: Schematische Darstellung der Geschwindigkeitskomprimierung durch Beschleunigung. Dopplereffekt (∆ν: Dopplerverschiebung, δν: Dopplerverbreiterung): v ∆ν = γβν ≈ ν c ν δν = δv c 2 c δE = m ∆ν δν ν = const ∆ν δν ist eine Konstante → je größer die Linienverschiebung, desto schmaler wird die Linie. Falls ein ruhendes thermisches Gas der Temperatur T um eU beschleunigt wird, erhält man: Abbildung 11: Typischer Aufbau für kollineare Spektroskopie. Quelle: Artikel von E.W. Otten in Bromley, Bd. 7. 11 Abbildung 12: Photodetachment- und Spektroskopieeinheit des LAMPF Experiments. Quelle: D.W. MacArthur et al., Physical Review A56, 282 (1986). δνDoppler (v) = s kT δνDoppler (0) 4eU (1) Beispiel: T = 2000 K U = 60 kV λ = 535 nm → δνDoppler ≈ 1 MHz In Realität werden Breiten von 10-50 MHz beobachtet (Schwankungen der Hochspannungsversorgung etc.). Anmerkung: Umladung ist auch geeignet für die Herstellung metastabiler Atome. 1.5 Elektronenablösung (Photodetachment) von negativen Ionen Kollisionsfreie Umladung, da durch Laser. Beispiel: extrem relativistischer Wasserstoffstrahl am LAMPF ( Los Alamos Meson Production Facility). Verwendet wird ein 800 MeV H− -Strahl (β = 0.84) (Abbn. 12 und 13). 12 Abbildung 13: LAMPF meson facility, Los Alamos. 2 Nachweis von Atomen • direkter Nachweis des Teilchens im Detektor • indirekt, z.B. durch optische Beobachtung von Resonanzfluoreszenz Historisch: z.B. makroskopischer Niederschlag des Atomstrahls auf einer Auffangplatte und anschließendes Wiegen; oder Erwärmung eines Bolometers (jetzt wieder aktuell mit kryogenen, supraleitenden Bolometern). Gewünscht: Einzelatomnachweis Neutrale Atome mit typischen thermischen Energien von 1 eV sind schwer direkt in einem Detektor nachweisbar. • Beobachtung durch Resonanzfluoreszenz. Diese Methode ist besonders empfindlich bei der Verwendung von geschlossenen Übergängen (‘cycling transitions’): Kann das mit dem Laser angeregte Atom nur in den ursprünglichen Zustand zurückfallen, kann dasselbe Atom sofort wieder angeregt werden usw. Für erlaubte elektrische Dipolübergänge sind Photonenstreuraten von 107 sec−1 leicht zu realisieren und erlauben die Detektion von wenigen (oder sogar einzelnen) Atomen mit Resonanzfluoreszenz, ohne daß dabei das Atom wie z.B. bei der Ionisation ‘zerstört’ wird. D.h. man kann z.B. in einer Falle die gleichen Atome über Minuten hinweg über ihre Resonanzfluoreszenz verfolgen. Oft verhindert jedoch schon die Existenz der Hyperfeinaufspaltung des Grundzustandes (typ. einige GHz) einen geschlossenen Übergang. • Umwandlung in ein Ion (z.B. durch Elektronenstoß, auf Oberflächen oder durch Photoionisation); anschließend Beschleunigung und effiziente Detektion in Zählern für geladene Teilchen. Beispiel für direkte Atomdetektion: metastabile Atome, wie z.B. im LAMB - RETHERFORD Experiment. Auf einer Oberfläche kann das metastabile Atom abgeregt werden und die gewonnene Energie zum Ausstoß eines Elektrons verwendet werden (Abbn. 14 und 15). 2.1 Zähler für geladene Teilchen Hier beschränken wir uns auf Energien unterhalb des MeV-Bereichs. 13 Abbildung 14: Aufspaltung des n=2 Zustandes in Wasserstoff. Quelle: Haken-Wolf. Abbildung 15: Das Experiment von L AMB und R ETHERFORD. W.E. Lamb und R.C. Retherford, Physical Review 72, 241 (1947). Bildquelle: Haken-Wolf. 14 Abbildung 16: Prinzip des Elektronenvervielfachers. Quelle: Moore, Seite 339. • Direkte Strommessung (Faraday cup): nicht empfindlich • Sekundärelektronenvervielfacher (‘electron multipliers’) Herkömmlicher Sekundärelektronenvervielfacher Verwandt mit dem Photomultiplier (siehe Kapitel über Spektroskopie). Abb. 16 zeigt den schematischen Aufbau. Als Dynodenmaterial wird z.B. eine Be-Cu-Legierung mit hoher Austrittsarbeit verwendet, um thermisch erzeugte Elektronen (Dunkelrate) zu unterdrücken. Nachteil: ein einfallendes Teilchen muß einige hundert eV Energie haben. Verstärkung: etwa 3 Sekundärelektronen pro Primärteilchen pro Stufe, d.h. mit 10-20 Dynoden werden Verstärkungen zwischen 106 und 107 erzielt. Die Zeitdispersion an der Anode beträgt typisch 10 ns. Der Ausgangspuls hat eine Höhe von 500 µV bis 500 mV, d.h. einzelne einfallende Teilchen sind leicht zu detektieren. Keine Ortsauflösung. Kontinuierliche Dynode: das Channeltron Im Channeltron wird die Dynodenstruktur durch eine kontinuierliche Metalloxidschicht mit hohem Widerstand (100 MΩ) ersetzt. Die Verstärkung kann wieder bis zu 108 betragen (Abb. 17). Microchannelplate: ortsauflösend 15 Abbildung 17: Prinzip des Channeltrons. Quelle: Moore, Seite 340. Abbildung 18: Microchannelplates. Quelle: Leo, Seite 174 Das Microchannelplate (MCP) (Abb. 18) setzt sich aus unzähligen Kapillaren zusammen (Innendurchmesser ≈ 10µm, Länge ≈ 0.5 mm). Jede Kapillare funktioniert wie ein Channeltron. Die Anode (oder ein nachgeschalteter Phosphorschirm) kann ortsauflösend ausgelesen werden. Durch den kurzen Weg der Elektronen von der Kathode zur Anode werden Zeitauflösungen im 100 ps-Bereich erzielt. Zählraten bis zu 105 sind möglich. MCPs sind mit bis zu 4 Inch Durchmesser erhältlich. Weiterer Vorteil der Umwandlung von Atomen in Ionen: vor der Detektion kann noch eine Massenfilterung, z.B. in einem RF-Quadrupolmassenfilter (siehe Kapitel über Ionenspeicherung) zur Untergrundunterdrückung vorgenommen werden. Anmerkung: alle vorgestellten Ionendetektoren können auch als Photonendetektoren eingesetzt werden, wenn eine Photokathode zum Einsatz kommt, d.h. das einfallende Photon startet die Kaskade durch den Photoeffekt (siehe Spektroskopie-Kapitel). 16 Abbildung 19: Ionisationsenergien und Austrittsarbeiten für diverse Elemente. Quelle: Scoles Band 1, Seite 169. 2.2 Ionisation von Atomen Oberflächenionisation Atome mit Ionisationsenergie EI treffen auf eine Oberfläche eines Materials mit einer Austrittsarbeit für Elektronen φ. Der Ionisationsgrad der Atome ist dann gegeben durch die S AHA -L ANGMUIRGleichung: s+ e(φ − EI ) = exp . (2) s0 kT Nach der Ionisation wird das Ion durch die attraktive Kraft seiner induzierten Spiegelladung an der Oberfläche festgehalten und kann nur durch thermische Energie entweichen. Typischerweise sollte φ mindestens 0.5 V größer sein als EI zur (fast) vollständigen Ionisation. Standarddetektor für schwere Alkalis: heißer (1000-2500 K) Wolframdraht (‘hot wire ionization detector’). Die Reinheit des Drahtmaterials ist wesentlich. Resonante Laserionisation Vorteil: • Atom wird im Vakuum ionisiert, keine komplizierten Oberflächeneffekte. • Beim Einsatz von gepulsten Lasern kann durch Flugzeitmessung (‘time-of-flight’) massenselektiert werden. 17 • Mehrstufige (resonante) Laserionisation ist extrem elementspezifisch und in vielen Fällen isotopenspezifisch (Isotopentrennung mit Lasern). Anmerkung: Einstufige (nichtresonante) Ionisation erfordert für die meisten Elemente Laser im VakuumUV. Resonante Laserionisation ist vermutlich die empfindlichste Methode, um aus einem makroskopischen Ensemble extrem seltene Elemente/Isotope nachzuweisen (Spurenelementanalyse, Kernwaffentests etc., siehe Beispiel). Beispiel: G. Herrmann et al., Physikalische Blätter 50, 929 (1994). Feldionisation Im (z.B. homogenen) elektrischen Feld sieht das Elektron ein modifiziertes Potential, gezeigt in Abb. 20. Es bildet sich ein Sattelpunkt. Elektronen oberhalb der Sattelpunktsenergie ESP können dem Atom durch Feldionisation entkommen. Klassisch betrachtet ergibt sich eine Sattelpunktsenergie und eine zugehörige Sattelpunktshauptquantenzahl (wasserstoffähnliches Atom) s ESP = − nSP v u u = Zt 4e3 E Z 4π0 Ry 3 EZ 2( e4π )1/2 0 , wobei Ry= 13.6 eV und E die elektrische Feldstärke sind. Z ist die effektive Rumpfladung. In diesem simplen Modell sind z.B. die Verschiebungen der atomaren Zustände durch den Starkeffekt in keiner Weise berücksichtigt. Insbesondere beim Wasserstoff (l-Entartung, linear Starkeffekt) ist dieses Modell qualitativ. Bei im Labor zugänglichen elektrischen Feldern findet Feldionisation nur bei relativ großen Hauptquantenzahlen n statt. Beispiel: Zeff = 1, E = 1000V/cm → nSP = 24. Daher ist Feldionisation relevant für sog. Rydbergatome, d.h. Atome mit einem Valenzelektron weit außerhalb des Atomrumpfes. Rydbergatome haben außergewöhnliche Eigenschaften, wie Abb. 21 zeigt. Extrembeispiel: Bariumatome in n = 500. Der Radius der Elektronenbahn beträgt dann 25 µm und die spontane Lebensdauer 1 sec (J. Neukamer et al., Phys. Rev. Lett. 59, 2947 (1987)). Semiklassische Formel für die spontane Lebensdauer von angeregten Zuständen in wasserstoffartigen Systemen nach Marxer und Spruch (Phys. Rev. A43, 1268 (1991)): τ (n, l) ≈ τ0 n3 l(l + 1) Z4 τ0 ≈ 93.42 psec Atome können, meistens durch Mehrphotonenanregung, in Rydbergzustände gehoben werden und dann mit moderaten Feldern feldionisiert werden. 18 Zur Sättigung des ersten Anregungsschritts ist in der Regel nur wenig Intensität notwendig (I1 ≈ 10 mW/cm2 ). Der zweite Schritt erfordert mehr, je nach zu erreichendem n typisch 1-100 W/cm2 . Feldionisation ist sehr zustandsselektiv: der Übergangsbereich zwischen Ionisation und Nichtionisation ist nur wenige 10−7 eV und damit meistens schmaler als der Abstand von n nach n + 1. Beispiel für Feldionisation: Messung zur Unterdrückung des spontanen Zerfalls in einem Resonator R.G. Hulet, E.S. Hilfer und D. Kleppner (MIT), Phys. Rev. Lett. 55, 2137 (1985). Idee: Spontane Emission eines Photons durch ein angeregtes Atom kann aufgefaßt werden als Emission stimuliert durch das Vakuumfeld. Befindet sich das angeregte Atom zwischen zwei ‘unendlich’ ausgedehnten leitenden Feldplatten, wird die Modenstruktur des Vakuums modifiziert; Moden, die an den leitenden Platten elektrische Felder parallel zur Oberfläche erfordern, können nicht aufgebaut werden und spontane Emission in diese Vakuummoden hinein wird unterdrückt. Der schematische Aufbau des Experiments ist in Abb. 23 gezeigt. Cs-Atome werden in zwei Schritten nach n = 22, m = 2 gepumpt (Anregung und Experiment im elektrischen Feld, deshalb ist l keine gute Quantenzahl). Weiterhin werden Hochfrequenzübergänge genutzt, um die Atome in einen ‘circular state’ mit n, m = n − 1 zu pumpen. Spontaner Zerfall ist dann nur mit ∆m = −1 nach n = 21, m = 20 möglich. Im Zerfallsresonator liegt ein elektrisches Feld an, das die Quantisierungsachse definiert. ∆m = −1-Übergänge erfordern ein induziertes Übergansdipolmoment senkrecht zur Quantisierungsachse, was wiederum zu elektrischen Feldern parallel zur Leiteroberfläche führen würde. Beträgt der Plattenabstand d weniger als λ/2 (Wellenlänge der spontanen Strahlung, ≈ 0.45 mm), wird der Zerfall in diese Mode unterdrückt. Im Feldionisator, einem zugespitzten Kondensator, nimmt die Feldstärke kontinuierlich zu. Zuerst werden die n = 22 Atome ionisiert, etwas später die n = 21 Atome. Das Verhältnis der beiden beobachteten Raten in Abhängigkeit vom Plattenabstand d gibt Aufschluß über die spontane Zerfallsrate im Resonator. Ergebnisse sind in Abb. 24 dargestellt. 19 20 E E r r ESP 2 V = -Ze /4πε0r 2 V = -Ze /4πε0r + eE r Abbildung 20: Modifikation des Potentials im externen elektrischen Feld, stark überhöht gezeichnet. 21 Abbildung 21: Vergleich zwischen ‘normalen’ und Rydbergatomen. Quelle: Demtröder, S.460 Abbildung 22: Parameter für Feldionisation. Quelle: Demtröder, S.461 22 (a) (b) n=22,m=21 n=22, m=2 m=3 ... ∆m= -1 λ=0.45 mm E E Dye Laser 1 6s (c) Feldionisator Anregungszone Cs Quelle Cs 6s1/2 n=21,m=20 Dye Laser 2 D Zerfallsresonator n=22 |m|=21 + - d n=22 2 Dye Laser Hochfrequenz elektrisches Feld n=21 Abbildung 23: Prinzip des Experiments zur Modifikation der spontanen Lebensdauer von Rydbergatomen in einem Resonator. (a) Dipolabstrahlung im Falle eines induzierten Dipolmoments senkrecht zur Quantisierungsachse (∆m = ±1). (b) Anregung von Cäsium in den n = 22, m = 21 Zustand, die Hochfrequenzanregung findet durch ‘rapid adiabatic passage’ statt (hier nicht näher erläutert), Energieskala nicht im Maßstab. (c) Schema des experimentellen Aufbaus. Abbildung 24: Ergebnis der Messung zur Modifikation der spontanen Emission. Kurve (b) zeigt ein Flugzeitspektrum der unzerfallenen Atome für d < λ/2. Bei (a) ist d > λ/2. (Auch Scannen will gelernt sein). 23 3 Optische Spektroskopie 3.1 Allgemeines Zugang zu den Energieniveaus in Atomen und Molekülen durch Wechselwirkung mit Photonen. Laser und Hochfrequenztechniken haben diesem Gebiet zu überragender Präzision verholfen. Atomare Systeme können in einem extrem weiten Energiebereich durch Photonen an/abgeregt werden: • Bindungsenergie des wasserstoffähnlichen Urans im Grundzustand ist EB = Z 2 Ry ≈ 115keV, also im Röntgen/Gammastrahlenbereich. • Anregung innerer Schalen: eV bis viele keV • Valenzelektronen im eV Bereich (IR, optisch, UV) • Feinstruktur: 10 GHz bis 1 eV • Hyperfeinaufspaltung: MHz bis 50 GHz (HF, Mikrowellen) • Mokelüle: – Rotationsniveaus: Erot = h̄2 J(J + 1)/2I, 10−4 ..0.1 eV, mittleres IR bis Mikrowellen (λ = 1cm..25µm). – Vibrationszustände: Ev = h̄ω(v + 1/2), 10−2 ..1eV, λ = 0.1mm..1µm. Optische und RF Spektroskopie sind sicherlich am weitesten perfektioniert worden und werden hier näher besprochen. Historisch: ‘Passive’ Beobachtung von spontaner Emission mit Spektrographen. Die Probe wird z.B. durch Stoß (Entladung) angeregt und der Zerfall optisch beobachtet. Die dabei entdeckten Linienspektren sind der Anfang der Quantenphysik. 1868 wurde das Element Helium im Spektrum der Sonne während einer Sonnenfinsternis von J.N. Lockyear ‘entdeckt’. Mitte des 19. Jahrhunderts beobachtete Fizeau das Na-Dublett mit einem Interferometer, lange bevor diese Aufspaltung als Feinstruktur (Spin- Bahn-Kopplung) erkannt wurde. Auch heute sind passive Methoden aktuell, vor allem natürlich in der Astronomie (CCD revolutioniert Spektrographen). Im Labor z.B. sog. ‘beam-foil’ Spektroskopie zur Messung der Lebensdauer angeregter atomarer Zustände (siehe Abb. 26). Ansonsten aber dominieren heute aktive Techniken: Resonante Anregung mit Laserstrahlung. 3.2 Wechselwirkung zwischen Atom und Strahlung Vereinfachte Annahme eines Zweiniveausystems: Die Einsteinkoeffizienten sind natürlich von den Details im Atom abhängig. Für die stimulierten Prozesse werden sie quantenmechanisch, z.B. in Störungtheorie berechnet (siehe z.B. [8] etc.). Im 24 Abbildung 25: Elektromagnetisches Spektrum. Quelle: http:// bvsd.k12.co.us/ cent/ science/ Spectra%20Images/ SpectraImages.html. Abbildung 26: Aufbau zur beam-foil Spektroskopie und typisches Spektrum. Quelle: BergmannSchäfer, Band 4, Seite 234/35. 25 Abbildung 27: Zweiniveauatom mit den Strahlungsprozessen, die durch die Einsteinschen Koeffizienten beschrieben werden. Wab beschreibt die Wahrscheinlichkeit einer An- bzw. Abregung und ρ(ν) ist die Strahlungdichte des elektromagnetischen Feldes. Rahmen dieses Skripts soll nur eine Beziehung zwischen den Bab und dem spontanen Koeffizienten A21 mithilfe der Planckschen Strahlungsformel hergeleitet werden. Weiterhin soll die spontane Zerfallsrate durch eine klassische Herleitung plausibel gemacht werden. Die Relation zwischen A und B kann aus dem Gleichgewicht zwischen einer thermischen Verteilung von Atomen (Maxwell-Boltzmann) und einem Strahlungsfeld (Planck) abgeleitet werden. Im Gleichgewicht sind Anregung und Abregung von Atomen gleich häufig: (A21 + B21 ρ(ν)) n2 = B12 ρ(ν) n1 . Die Boltzmannverteilung ergibt: ! n2 g2 hν = exp − , n1 g1 kT wobei ni die Populationen der beiden Zustände sind und gi die jeweiligen statistischen Gewichte. Aus den beiden obigen Gleichungen erhält man: 26 ρ(ν) = g1 B12 g2 B21 A21 /B21 . exp (hν/kT ) − 1 Weiterhin wird ρ aber natürlich durch die Plancksche Strahlungsformel beschrieben: 8πν 3 h 1 ρ(ν) = . 3 c exp (hν/kT ) − 1 Hieraus ergibt sich: g1 B12 = g2 B21 8πhν 3 A21 = B21 . c3 Diese Herleitung beruht auf dem Gleichgewicht mit thermischer Strahlung, die Relationen gelten aber für beliebige Strahlungsfelder. Übergangsraten In der elektrischen Dipolnäherung betrachtet man die Wechselwirkung zwischen dem elektrischen Feld der Lichtwelle und dem elektrischen Dipolmoment des Atoms. Allerdings haben Atome kein permanentes elektrisches Dipolmoment, denn dies würde zu einer Verletzung der Zeitumkehrinvarianz führen. Abbildung 28 illustriert diese Tatsache. Die Suche nach extrem kleinen permanenten elektrischen Dipolmomenten in Atomen und Neutronen ist derzeit ein aktives Forschungsgebiet (z.B. Commins/Berkeley, Fortson/Seattle, DeMille/Yale, Hinds/Sussex etc.), hier kann die Atomphysik mit der Hochenergiephysik bei der Erforschung des Standardmodells und potentieller Erweiterungen konkurrieren. Abbildung 28: Suche nach einem permanenten elektrischen Dipolmoment (EDM). Quelle: FortsonGruppe, Univ. of Washington, Seattle; www.phys.washington. edu/ ˜ romalis/EDM/. Diese möglichen winzigen permanenten Dipolmomente haben natürlich nichts mit unseren elektrischen Dipolübergängen in Atomen zu tun. In diesem Falle wechselwirkt das elektrische Feld der Lichtwelle mit einem elektrischen Übergangsdipolmoment. 27 Eine Überlagerung zweier Zustände entgegengesetzter Parität erzeugt ein oszillierendes Übergangsdipolmoment. Dieses Phänomen ist an einem einfachen 1-D “Atom” im Berkeley Physics Course (Vol. 3 ,S. 557) anschaulich erläutert: überlagert man die untersten beiden Zustände im 1-D Kastenpotential (bei einer Spiegelung an der Kastenmitte ist der Grundzustand symmetrisch, der erste angeregte Zustand antisymmetrisch, d.h. die Parität ist verschieden), erhält man eine hin- und herlaufende Ladungsdichte mit einer Oszillationsfrequenz |E2 − E1 | , h d.h. das “Atom” strahlt auf der Frequenz ν21 elektromagnetische Strahlung ab. Wie kommt es aber zu einer solchen Überlagerung ? Im Falle der stimulierten Prozesse kann man sich vorstellen, daß das elektrische Feld der Lichtwelle das Elektron bzgl. des trägen Kerns “hin- und herschüttelt” und damit die Überlagerung schafft. In Analogie zu getriebenen klassischen Oszillatoren hängt es von der Phase zwischen Welle und Oszillator ab, ob dem Oszillator Energie hinzugefügt (stimulierte Absorption) oder entzogen wird (stimulierte Emission). Abbildung 29 zeigt das oszillierende Moment für s-p Übergänge. ν21 = Abbildung 29: Oszillierendes elektrisches Übergangsdipolmoment. Quelle: Siegmann, Seite 140; (special thanks to Guido Saathoff). Bei der spontanen Emission ist es intuitiv schwieriger, diese Überlagerung zu verstehen. Um diesen Prozeß richtig zu berechnen, muß man zur Quantenelektrodynamik übergehen. Auch ohne eine externe Anregung ist das gemittelte Quadrat der elektrischen Feldamplitude < E 2 > nicht Null aufgrund der sog. Vakuumfluktuationen (analog zur Nullpunktsenergie des quantenmechanischen harmonischen Oszillators, diesen Fluktuationen sind wir schon im Kapitel über Feldionisation begegnet). Mit einigen “leaps of faith” kann man die spontane Emission klassisch sehr einfach herleiten. Klassisch strahlt eine beschleunigte Ladung die Leistung 28 P = = = = 2 e2 v̇ 2 3c3 4π0 4 2 1 2 v e 3 4π0 c3 r2 4 2 ω (e · r)2 3 4π0 c3 2 ω4 D2 , 3 4π0 c3 ab, wobei von Gl. 1 nach 2 eine kreisförmige Bewegung angenommen wurde und D = e · r das elektrische Dipolmoment definiert. Nun setzt man ad hoc für das Dipolmoment das quantenmechanische Übergangsdipolmoment ein: D = e Z ψ1∗ r ψ2 d3 r. Mit P = h̄ω21 A21 erhalten wir Afastrichtig = 21 3 16 π 3 ν21 D2 . 6 0 hc3 Dieses Ergebnis unterscheidet sich um einen Faktor 1/2 vom richtigen Resultat (vermutlich Polarisation?). Eine Möglichkeit zur “Beschaffung” dieses Faktors kann man in Demtröder, S. 34 finden. In Quantum Mechanics von I. Schiff wird die ganze Rechnung ausführlich dargestellt. Abschliessend seien nun die Einsteinkoeffizienten noch einmal gelistet (B hängt davon ab, ob man ρ(ν) oder ρ(ω) verwendet): 3 16 π 3 ν21 |D|2 3 0 hc3 2 π2 = |D|2 2 3 0 h π = |D|2 2 3 0 h A21 = ν B21 ω B21 3.3 Linienbreiten Natürliche Linienbreite Hier verwenden wir wieder ein klassisches Modell: bei spontaner Emission wird durch das oszillierende Dipolmoment elektromagnetische Leistung abgestrahlt, was die Oszillation dämpft. Die Abstrahlung soll nun durch einen klassischen gedämpften harmonischen Oszillator beschrieben werden. ẍ + γ ẋ + ω02 x = 0, q wobei ω0 = k/m. Unter der Annahme schwacher Dämpfung (γ 2 ω02 , gerechtfertigt für erlaubte optische Übergänge im Sichtbaren, wo ω0 ≈ 5 × 1014 Hz und A21 ≈ 108 Hz) erhält man als reelle Lösung (siehe z.B. Greiner, Bd. 1) mit x(0) = x0 , ẋ(0) = 0: 29 x(t) = x0 exp mit ω = −γt 2 cos ωt, q ω02 − γ 2 /4. Das Energiespektrum erhalten wir durch eine Fouriertransformation: 1 Z∞ A(ω) = √ x(t) exp (−iωt)dt 2π −∞ 1 Z∞ = √ x0 exp (−γ/2 t) cos ωt exp (−iωt)dt. 2π −∞ Daraus resultiert ein komplexes A(ω): A(ω) = q γ/2π i . ω0 − ω + iγ/2 Das Intensitätsspektrum wird durch I = A∗ A beschrieben: I(ω) = γ/2π , (ω0 − ω)2 + γ 2 /4 gültig für γ ω0 , |ω0 − ω| ω0 . Das Profil G(ω0 − ω) = γ/2π (ω0 − ω)2 + γ 2 /4 wird Lorentz-Profil genannt undR beschreibt die natürliche Linienform einer atomaren Linie. In der hier verwendeten Form ist 0∞ G(ω0 − ω)dω = 1. D.h. ein Vorfaktor wäre ein Indikator für die Gesamtstärke der Linie. Volle Halbwertsbreite γ der Lorentzkurve (FWHM für full width at half maximum): γ = δωn δνn = γ/2π = A21 /2π = 1 , 2πτ2 hierbei ist τ2 die spontane Lebensdauer des angeregten Zustands. Alternativ kann man die Linienbreite auch mit Hilfe der Heisenbergschen Unschärferelation bestimmen: ∆E 1 = . δν = h 2πτb Schließlich kann man auch auf Übergänge zwischen zwei angeregten Zuständen verallgemeinern: δνab = 1 1 (γb + γa ) = 2π 2π Beispiele für natürliche Linienbreiten: 30 1 1 + . τb τa • Natrium D-Linie (3p → 3s): τ3p = 16 nsec → δν = 10 MHz. Dieser Wert ist typisch für erlaubte elektrische Dipolübergänge (E1) in neutralen Atomen. • 2s-Zustand in Wasserstoff: ∆l = 0 → kein E1 erlaubt, im feldfreien Raum Zerfall durch Zweiphotonenabregung (siehe unten). τ2s ≈ 0.15 sec → δν = 1 Hz! Anmerkung: die zur optischen Spektroskopie zur Verfügung stehenden durchstimmbaren Laser (Farbstofflaser, Diodenlaser) können routinemäßig auf etwa 1 MHz Linienbreite stabilisiert werden und sind daher ausreichend schmal zur Spektroskopie erlaubter Übergänge. 3.3.1 Verbreiterungsmechanismen Stoßverbreiterung 1. inelastische Stöße regen den oberen Zustand strahlungslos ab und verkürzen damit die Lebensdauer, dadurch wird δν größer. 2. elastische Stöße führen zu Verbreiterungen und Linienverschiebungen. Findet die An- oder Abregung während eines nahen Vorbeifluges zweier Atome statt, sind die Bindungsenergien im Atom gegenüber den Eigenzuständen des isolierten Atoms verschoben (in der Regel um verschiedenen Beträge für Anfangs- und Endzustand). Dies ist in Abbildung 30 illustriert. E |2> |1> R Abbildung 30: Illustration der Linienverschiebung bei Kollisionen im Gas. R ist der internukleare Abstand und die beiden Potentialkurven stellen die Energiezustände im zu spektroskopierenden Atom dar. Beispiel: Natrium D-Linie, Natrium in Argongas: δν = 23 MHz/ mbar, Verschiebung = −6 MHz/mbar. 31 Durchflugsverbreiterung (time-of-flight broadening) Wird die Durchflugszeit T durch den anregenden Laser kleiner als die Lebensdauer des atomaren Zustandes, dominiert die Durchflugszeit die Linienbreite (Abb. 31). Atomstrahl d Laser Abbildung 31: Durchflugsverbreiterung. Abrupte Anregung: Z A(ω) ∝ t=T t=0 E0 cos ω0 t exp (−iωt) dt 0 (sin ω−ω T )2 2 , (ω − ω0 )2 → I(ω) ∝ mit |ω − ω0 | ω0 . Für eine solche Anregung ergibt sich dann δωtofu ≈ 5.6 . T In der Regel wird der Laserstrahl jedoch ein gaussförmiges Profil besitzen, dann erhält man v δωtof,Gauss ≈ 4.7 . d Beispiel: • Na (vtherm ≈ 1000 m/s), d = 1 cm: → δνtof = 75 kHz, dies ist unbedeutend im Vgl. zur natürlichen Linienbreite. • Li+ Ionenstrahl: Ekin = 200 eV, d = 1 mm → δνtof ≈ 50 MHz, dies ist groß im Vgl. zur natürlichen Linienbreite von δνn = 4 MHz. Molekulare Schwingungsanregungen haben oft spontane Lebensdauern im msec- Bereich, hier kann es bereits bei thermischen Molekularstrahlen zur Durchflugsverbreiterung kommen. Dopplerverbreiterung Dopplereffekt: ν 0 = ν0 γ (1 + β cos θ), mit dem Winkel θ zwischen Laser und Atomstrahl. Im Folgenden sei β 1, d.h. ω 0 = ω0 (1 + β cos θ) und der Laserstrahl laufe entlang der z-Richtung. Im thermischen Gleichgewicht erhalten wir dann die Anzahl dn der Atome mit Geschwindigkeit vz : dn(vz ) = N √ vw vz exp − π vw 32 2 dvz , wobei vw die oben definierte wahrscheinlichste Geschwindigkeit ist. Ersetzt man nun vz durch das durch den Dopplereffekt zugehörige ω, erhält man: Nc c ω − ω0 √ exp − dn(ω) = vw ω0 π vw ω0 2 dω. Der Dopplereffekt führt also zu einer Gaußverteilung mit Halbwertsbreite (FWHM): δνD ν0 = c s 8 kT ln2 = 7.16 × 10−7 ν0 m s T , M wobei der letzte Ausdruck die Breite in Hz angibt, wenn T in K und M als Molmasse eingesetzt wird. Beispiel: Na D-Linie, λ = 589 nm, T = 500 K → δνD = 1.7 GHz, dies ist viel größer als die natürliche Linienbreite. Es besteht ein qualitativer Unterschied zwischen natürlicher und Dopplerbreite: die Gaußfunktion fällt in den Flügeln exponentiell ab, das Lorentzprofil hat hingegen sehr weite Flügel. Es gibt oft Situationen, wo weder die natürliche noch die Dopplerverbreiterung vernachlässigt werden können. In diesem Falle muß das Lorentzprofil mit einer Gaußfunktion gefaltet werden, und man erhält das sog. Voigtprofil (Abb. 32): I(ω) ∝ Z 0 ∞ dω 0 2 c ω−ω 0 0 vw ω , ω 0 )2 + γ 2 /4 exp − (ω − es gibt keine analytische Darstellung für das Voigtprofil, daher ist es etwas schwierig zu handhaben. Abbildung 32: Voigtprofil, Quelle: Demtröder, S. 56. 33 Homogene und inhomogene Verbreiterungen Ist für eine bestimmte Lichtfrequenz ν die Wahrscheinlichkeit einer Anregung für alle Atome/Moleküle gleich, handelt es sich um eine homogene Verbreiterung, ansonsten spricht man von inhomogener Verbreiterung. Die Dopplerverbreiterung ist der wichtigste Vertreter der inhomogenen Effekte. Alle anderen vorgestellten Mechanismen sind homogen (mit Ausnahme gewisser Stoßprozesse). 3.3.2 Sättigung und Sättigungsverbreiterung Im Folgenden wird gezeigt, daß ein Atom nicht beliebig viele Photonen pro Zeiteinheit streuen kann, sondern daß bedingt durch die Existenz der stimulierten Emission eine Sättigung der Streuung einsetzt. Annahme: Zweiniveausystem mit (zunächst) gleichen statistischen Gewichten (d.h. B12 = B21 = B, A21 = A, weiterhin sind N1,2 die Populationen von Grund- und angeregtem Zustand und N = N1 + N2 ), keine Stöße. dN1 dN2 = − = −Bρ N1 + Bρ N2 + A N2 . dt dt Im stationären Fall erhält man: BρN2 + AN2 − BρN1 = 0, und damit N1 = Bρ + A N. 2Bρ + A Hier kann man bereits einen wichtigen Schluß ziehen. Für schwache Strahlungsfelder (ρ → 0) sind fast alle Atome im Grundzustand (N2 ≈ 0). Im Limit ρ → ∞ hingegen stellt man fest, daß N1 → N/2. D.h. man kann nie mehr als die Hälfte der Atome in den angeregten Zustand heben , also gilt immer N2 < N1 und ∆N = N1 − N2 > 0. ∆N = N 1 1 + 2Bρ A Die Absorption dieses Ensembles von N Atomen ist gegeben durch: α12 tot = σ12 tot ∆N = σ12 tot N 1 , 1 + 2Bρ A d.h. die Absorption ist der Unterschied von Anregungsrate (∝ N1 σ12 tot ) und stimulierter Emissionsrate (∝ N2 σ12 tot ). Für hohe Laserintensitäten wird die Absorption kleiner, und im Limit unendlicher Intensität wird das Medium transparent, man spricht von Sättigung des Mediums und definiert den Sättigungsparameter S = 2Bρ , A der proportional zum Verhältnis der stimulierten Abregungsrate zur spontanen Abregung ist. 34 Die bisher verwendeten Einsteinkoeffizienten sind integral über die Resonanz definiert. Um die Sättigung frequenzabhängig über die Linienbreite zu untersuchen, betrachten wir jetzt den frequenzabhängigen Absorbtionswirkungsquerschnitt. Die Übergangswahrscheinlichkeit kann man auf zwei Weisen betrachten: W12 = B12 ρ(ν) = σ12 tot I , hν wobei I/(hν) den Fluß einfallender Photonen angibt, wenn I die Laserintensität ist (z.B. in W/cm2 ). Mit I = ρc folgt dann ω σ12 tot = B12 h̄ω . 2πc Von W12 = σ12 tot I hν verallgemeinern wir zu W12 (ω) = σ12 (ω) I hν und nehmen an, daß die Laserintensität I von der Frequenz unabhängig ist. Der frequenzabhängige Wirkungsquerschnitt hat natürlich Lorentzform: σ12 (ω) = σ12 tot G(ω − ω0 ) ω h̄ω G(ω − ω0 ) = B12 2πc πc2 A21 G(ω − ω0 ), = 2ω 2 wobei B mithilfe der hergeleiteten Relation in den spontanen Einsteinkoeffizienten verwandelt wurde. Damit kann auch ein frequenzabhängiger Sättigungsparameter bestimmt werden:1 2σ12 (ω)I A21 h̄ω 4πc2 I = L(ω − ω0 ), h̄ω 3 A21 S(ω) = mit der Definition γ 2 /4 . L(ω − ω0 ) = (ω − ω0 )2 + γ 2 /4 Hierbei handelt es sich wiederum um ein Lorentzprofil, jedoch mit anderer Normierung als im Falle von G(ω − ω0 ): ein Vorfaktor ergibt hier den Wert der Funktion in der Resonanzmitte. Diese Normierung ist hier vorzuziehen, da der Sättigungsparameter in den Flügeln des Profils bzgl. der Sättigung auf Resonanz ausgedrückt werden soll. Somit erhalten wir 1 In der folgenden Gleichung wird der zuvor hergeleitete Ausdruck für σ12 (ω) eingesetzt, und auf den ersten Blick scheinen sich dann die beiden A21 -Koeffizienten wegzukürzen. Gleichzeitig wurde jedoch die Lorentzfunktion anders normiert, d.h. von G nach L übergegangen. Dabei bleibt ein Faktor 1/γ übrig, aber γ und A21 sind synonym. Zugegebenermassen ist die Notation hier durchaus verbesserungsfähig. 35 S(ω) = I Isat L(ω − ω0 ) mit Isat = hπcA21 . λ3 Dieses Resultat für die Sättigungsintensität wäre korrekt für den unrealistischen Fall eines J = 0 → J = 0 Übergangs (seit beginn des Kapitels wurden die statistischen Gewichte der Zustände ignoriert!). Für den einfachsten realistischen Fall J = 0 → J = 1 muß man die statistischen Gewichte berücksichtigen und erhält (siehe Jackson, Electrodynamics, Kap. 17.8 für eine detaillierte Ausführung): Isat (J = 0 → 1) = hπcA21 , 3λ3 d.h. strahlt man mit einem schmalbandigen Laser auf der Linienmitte mit Intensität I ein, wird die Absorption um 1/(1 + I/Isat ) verringert. Verbleibt noch der Einfluß der Sättigung auf die Linienbreite. S(ω) = S0 L(ω − ω0 ) mit S0 = I/Isat . Damit ist α12 (ω) = σ12 (ω) ∆N = σ12 tot = σ12 tot γ/2π 1 (ω − ω0 )2 + γ 2 /4 1 + S(ω) γ/2π , 2 (ω − ω0 ) + (1 + S0 )γ 2 /4 somit√ hat der Absorptionskoeffizient auch unter Sättigung Lorentzform, aber mit der Halbwertsbreite γs = 1 + S0 γ, die Linie ist jetzt sättigungsverbreitert. Beispiel: erlaubte Dipolübergänge in Alkaliatomen (z.B. D1 , D2 ), haben Sättigungsintensitäten im Bereich von einigen mW/cm2 , dies ist mit durchstimmbaren Lasern leicht zu erreichen. Die meisten atomaren Übergänge sind durch ein Zweiniveausystem nur schlecht beschrieben, und deshalb muß obige Formel mit Vorsicht angewendet werden. Die Sättigung limitiert die maximale Streurate von Photonen (Absorption) an Atomen, dies ist z.B. wichtig für die Realisierung von Atomfallen (siehe unten). 36 3.4 Laserspektroskopische Methoden Mit dem Laser werden Übergänge angeregt. Als Signal wird entweder die Absorption oder die gestreute Fluoreszenz beobachtet. Im optischen Bereich steht eine grössere Anzahl von geeigneten Lasern zur Verfügung, die Hauptrolle spielen Farbstofflaser, Titan-Saphir-Laser und Halbleiterdiodenlaser (siehe Abb. 33). Abbildung 33: Frequenzbereich abstimmbarer Laser. Quelle: Demtröder, S. 233. Vorteile der Laserspektroskopie: • sehr hohe spektrale Auflösung, 1 MHz Standard, kHz bis Hz heute möglich • hohe Leistung, mW bis W für typische durchstimmbare Dauerstrichlaser (CW = continuous wave) Bild 34 vergleicht die Laserabsorptionsmethode mit herkömmlicher Spektroskopie. Abbildung 34: Absorptionsspektroskopie. Quelle: Demtröder, S. 283. Bei der Detektion schwacher Absorptionssignale ist es wichtig, daß die Laserintensität während des Scans stabil bleibt. Zwar kann man einen Vergleichsstrahl, der nicht der Absorption unterliegt, zum 37 Vergleich heranziehen, wie in Abb. 34 angedeuted, da aber die verschiedenen Photodioden keine identischen Kennlinien haben, ist dieser Methode eine Grenze gesetzt (“common mode rejection”). Abhilfe kann hier eine optische Intensitätsstabilisierung schaffen: eine elektronisch steuerbare Phasenplatte (z.B. aus Flüssigkeitskristallen) dreht die Polarisation des Laserlichts. Der folgende Analysator lässt nur einen Bruchteil entsprechend der Projektion der Polarisation auf seine Achse durch. Durch Anlegung einer Spannung an den Modulator kann die den Analysator durchlaufende Intensität somit elektronisch geregelt werden. Eine am Ausgang des Stabilisators befindliche Photodiode steuert über eine Rückkopplung den Modulator. Das Prinzip ist in Abb. 35 gezeigt und Abb. 36 zeigt die Wirksamkeit dieser Methode. Abbildung 35: Prinzip des ‘noise-eaters’. Quelle:www.cri-inc.com. Weitere Probleme sind Steulicht, das auf die Detektoren fällt, Rauschen in der Elektronik, so z.B. langsame Driften (DC-shift) und 50 Hz Störsignale, die man sich sowohl elektronisch als auch optisch über Fluoreszenzlampen einfangen kann. Eine extrem nützliche Methode zur Unterdrückung solcher Störungen ist die phasenempfindliche Detektion. 3.4.1 Frequenzmodulation und phasenempfindliche Detektion Die Laserfrequenz wird sinusförmig mit Frequenz Ω variiert, wobei der Modulationshub a klein gegen die Breite der absorbierenden Resonanz sein soll. Somit geht die langsame Frequenzrampe ωL (t) über in ωL (t) + a sin(Ωt). Schaut man dann das Absorptionssignal bei den Harmonischen der Modulationsfrequenz an, erhält man die Ableitungen des Absorptionsprofils (siehe Demtröder, Sec. 6.2.1) dα d2 α S(nΩ) ≈ a L const + sin(Ωt) − a/4 2 cos(2Ωt) − ... . dω dω " # Der Nachweis der Absorption erfolgt dann bei nΩ, am besten mit einem phasenempfindlichen Verstärker. Damit können Störquellen bei allen anderen Frequenzen und selbst Signale mit gleicher Frequenz aber falscher Phase eliminiert werden. 38 Abbildung 36: Ein- und Ausgangssignal der Intensitätsstabilisierung. Quelle: THORLABS Inc. Katalog. Lock-in-Verstärker Lock-in-Verstärker werden zur phasenempfindlichen Detektion verwendet. In Abbildung 38 ist das Prinzipschaltbild eines typischen Lock-in-Verstärkers gezeigt. Ein interner Oszillator, in Frequenz und Amplitude in weiten Bereichen einstellbar (subHz bis 100 kHz) kann von außen abgegriffen werden und wird zur Modulation des Lasers eingesetzt. Das Detektorsignal spiegelt diese Modulation wieder und wird in den Verstärkereingang gegeben. Dann wird das Signal mit der internen Referenz verglichen. Da die Elektronik und die Details des Experiments natürlich die Phase des Signals gegenüber der Referenz verschieben, muß noch die Möglichkeit zur Phasenanpassung gegeben sein. Der phasenempfindliche Detektor ist im wesentlichen ein Multiplikator/Integrator, heute oft digital ausgeführt. Am Ausgang erhält man ein DC-Signal, das proportional zur Amplitude der Signalmodulation im Detektor ist. Mit einem solchen System kann man in geeigneten Fällen die Empfindlichkeit ohne weiteres um einen Faktor 1000 steigern. 3.4.2 Laserinduzierte Fluoreszenz In diesem Falle wird nicht nach Absorption geschaut, sondern nach den gestreuten Photonen. Im Prinzip sollte diese Methode empfindlicher sein als Absorptionsmessungen, weil bei optimaler Streulichtunterdrückung kein Laserlicht direkt in den Detektor gelangt. In Fällen mit einer Abregung über Zwischenzustände kann man das Anregungslicht auch effektiv mit einem optischen Filter vor dem Photomultiplier blockieren. Ein Nachteil ist die Tatsache, daß die Fluoreszenz in den ganzen Raumwinkel gestreut wird, der Detektor technisch bedingt aber nur etwa einige Prozent Raumwinkel überdecken kann. Beispiel: Kernradienstudien mit neutronenarmen Yb-Isotopen (Abb. 39). In diesem Experiment wurde neutronenarmes Ytterbium in einer Kernreaktion on-line am Beschleuniger hergestellt (A=158152, stabile Yb-Isotope: A=168-176). Das Reaktionsprodukt wird durch den Impuls des beschleunigten Projektils durch das Target durchgestoßen und kommt in einer mit Edelgas gefüllten Zelle (einige 39 Abbildung 37: Ableitungen einer Resonanz. Quelle: Demtröder. mbar) zum Stillstand (die Yb-Atome diffundieren dann in etwa 100 ms zu den Wänden). In der Zellenmitte wird Laserspektroskopie durchgeführt. In diesem Aufbau wird viel Laserlicht durch das Puffergas in den Photomultiplier gestreut, die beobachtete Fluoreszenz hat die gleiche Wellenlänge wie die Anregung. Allerdings gibt es hier einen anderen Ausweg: die Lebensdauer des angeregten Zustands beträgt 800 nsec. Dies ist lange genug, um zuerst mit dem Laser die Atome anzuregen, dann den Laser abzuschalten und erst danach Fluoreszenz zu beobachten. Das schnelle An- und Ausschalten des Lasers (nsec-Schaltzeiten) wird mit einem akusto-optischen Modulator bewerkstelligt (siehe z.B. Saleh und Teich, Photonics [10]). Mit dieser Technik konnten Spektren bei 154 Yb mit einer Rate von nur 900 Atomen/sec gewonnen werden. 40 Abbildung 38: Lock-in-Verstärker und externe Beschaltung. Quelle: Stanford Research Systems, SRS830 Manual. Abbildung 39: Laserinduzierte Fluoreszenz, Beispiel Yb-Spektroskopie. Auch hier wurde Iodspektroskopie und Etalon-Frequenzmarker zur Frequenzkalibrierung verwendet. Quelle: SprouseGruppe, Stony Brook, NY. A. Berger et al., Nucl. Instr. and Meth. A 311, 224 (1992). 41 Abbildung 40: Laserinduzierte Fluoreszenz in Ytterbium, Teil 2. AO steht für akusto-optischer Modulator, der Modulator wird hier verwendet, um den Laserstrahl im 100 nsec Bereich an- und auszuschalten. Abbildung 41: Laserinduzierte Fluoreszenz in Ytterbium, Teil 3. 42 Abbildung 42: Laserinduzierte Fluoreszenz in Ytterbium, Teil 4. Abbildung 43: Laserinduzierte Fluoreszenz in Ytterbium, Teil 5. 43 3.4.3 Photoakustische Spektroskopie Im vorigen Beispiel konnte die relativ lange spontane Lebensdauer zur Untergrundunterdrückung genutzt werden. Werden die Lebensdauern noch länger, wie dies insbesondere bei Molekülen der Fall sein kann, hat man einfach zu wenig Absorption oder Fluoreszenz für ein vernünftiges Signal. Aber auch hier gibt es Lösungen: einer schnellen Anregung durch einen ausreichend kräftigen Laser läßt man eine schnelle strahlungslose Abregung durch Stöße folgen. Hierbei wird die vom Laser aufgenommene Energie in kinetische Energie verwandelt, was zu einer Druckerhöhung im Zellgas führt, wenn man sich auf Resonanz befindet. In typischen Zellen mit etwa 1 mbar erfolgt die Druckänderung in wenigen µsec. Unterbricht man den Laserstrahl mit einem “Chopper”, erhält man eine periodische Druckschwankung, die mit einem Mikrophon und Lock-in-Verstärker registriert wird (Abb. 44). Abbildung 44: Aufbau für die photoakustische Spektroskopie. Quelle: Demtröder, S. 302. Weitere Methoden der optischen Spektroskopie Es gibt eine Unzahl von weiteren Varianten der optischen Spektroskopie, hier seien einige wenige genannt: • Laserresonanzionisation (siehe oben) • FM-Seitenbandspektroskopie, Lasermodulationen im MHz- bis GHz-Bereich. • Optogalvanische Spektroskopie Mehr Informationen über diese und weitere Methoden findet man im Buch von Demtröder. 44 3.5 Nichtlineare Methoden zur dopplerfreien Spektroskopie 3.5.1 Sättigungsspektroskopie Sättigungsspektroskopie ist eine einfache Methode zur Unterdrückung des Dopplereffekts und wird sehr oft eingesetzt. Abbildung 45 erläutert das Prinzip: durch eine Gaszelle, z.B. mit Rb gefüllt, wird ein starker Laserstrahl geführt, der in der Lage ist, die zu untersuchende Resonanz zu sättigen. Nach dem Durchlauf wird der Strahl auf sich selbst rückreflektiert, weit unter Sättigungsintensität abgeschwächt und dann wieder durch die Zelle gesandt. Befindet sich der Laser nicht in der Mitte der Geschwindigkeitsverteilung, sprechen die zwei Strahlen zu verschiedenen Geschwindigkeitsgruppen, d.h. sie “merken” nichts voneinander. Der Sättigungsstrahl “brennt” ein Loch in die Grundzustandsverteilung N1 , die lokal auf etwa die Hälfte zurückgeht (angedeuted durch die gestrichelte Linie). Der Probestrahl hebt einen viel kleineren Teil hoch. Die beiden Strahlen kommen sich nur bei einer Geschwindigkeitsklasse (v=0) in die Quere. Dort sättigt der starke Strahl bereits alle Atome und der Probestrahl findet ein transparentes Medium vor. Deshalb hat die Absorption des Probestrahls bei v = 0 → ωL = ω0 einen lokalen Einbruch, den sog. Lambdip. Dieser ist ein dopplerfreies Merkmal für die Linienmitte. Sättigungsstrahl Probestrahl N2 v ω0 ωL N1 α v ω0 "Lambdip" Abbildung 45: Prinzip der Sättigungsspektroskopie. Ein typischer Aufbau für Sättigungsspektroskopie ist in Abbildung 46 gezeigt. Hier wird ein zweiter Probestrahl verwendet, der nicht mit dem Sättigungsstrahl überlappt. Dieser kann dann elektronisch vom anderen abgezogen werden und man erhält ein Signal, das nur die Lambdips zeigt und die Dopplerverteilung unterdrückt. Abbildung 47 zeigt die Signale für die Rubidium D2 Linie: Dopplerspektrum, Dopplerspektrum mit Lambdips und Lambdips mit subtrahiertem Doppleruntergrund. Abb. 48 zeigt das zugehörige Termschema. Die vier Dopplerresonanzen stammen von den Grundzustandshyperfeinaufspaltungen in den Isotopen 85 Rb und 87 Rb. Die beiden äußeren Peaks gehören zu 87 Rb und sind vergrößert in Abb. 49 gezeigt. Erstaunlicherweise erkennt man bis zu 6 Lambdips in jedem dieser Peaks, obwohl wir nur 3 Übergänge von jedem Grundzustandsniveau aus erwarten. Dies ist das Phänomen der Crossover-Resonanzen: 45 MO BS λ /2-Platte Speicheroszilloskop Sig.Out Ref. Out Lock In PD Sig. In Pumpstrahl D PD M Probestrahlen M M Rubidium-Zelle Sättigungsspektroskopie Abbildung 46: Aufbau zur Sättigungsspektroskopie. Abbildung 47: Sättigungssignal in Rb. Sättigung kann auch eintreten, wenn ein Atom auf einem Übergang gesättigt und auf einem anderen vom Probestrahl abgefragt wird. Befinde sich nun der Laser genau in der Mitte zwischen zwei Übergängen eines Grundzustandsniveaus. Dann gibt es eine Geschwindigkeitsgruppe von Atomen, die sich mit der passenden Geschwindigkeit bewegt, so daß sie den starken Laserstrahl auf eine der beiden Resonanzen dopplerverschoben sieht und somit gesättigt wird. Gleichzeitig ist dann natürlich der Probestrahl auf die andere Linie dopplerverschoben und sieht dort trotz erfüllter Resonanzbedingung nur ein transparentes Medium. Bei drei Übergängen kommt man dann auf 3 “echte” Lambdips und 3 weitere Crossovers (dies funktioniert natürlich nur, wenn die Dopplerverbreiterung größer ist als die Aufspaltung der Levels, deshalb gibt es natürlich keine Crossovers zwischen verschiedenen Grundzuständen). Sättigung in molekularem Jod Sättigungsspektroskopie in I2 ist eine wichtige Anwendung. Das Jodmolekül hat über den gesamten sichtbaren und nahen IR-Bereich Linien (Rotationsvibrationsspektren elektronischer Übergänge). Typischerweise findet man alle paar GHz eine solche Linie. Diese Linien wurden von Luc und Gerstenkorn vermessen und in einem Atlas zusammengefaßt. Wie schon in obigen Beispielen gezeigt, kann man bei der Spektroskopie beliebiger anderer Spezies einen Teil des Lichts abzweigen und 46 F F 3 267 MHz 4 124 MHz 2 3 5p3/2 157 MHz 1 72 MHz 0 63 MHz 2 1 29 MHz D2 Linie 780 nm 2 3 5s1/2 6 GHz 3 GHz 2 1 Rb 87 Rb 85 Abbildung 48: Termschema für die Rb D2 Linie. Abbildung 49: Sättigungssignal in Rb. 47 durch eine Jodzelle senden. Das simultan aufgenommene Jodspektrum dient dann zur absoluten Frequenzkalibration. Allerdings sind diese Linien wegen des Dopplereffektsetwa 1 GHz breit, was zu Genauigkeiten bis zu einigen 10 MHz führt. Nun kann man Sättigungsspektroskopie an Jod durchführen und die Hyperfeinstruktur auflösen. Damit erreicht man Genauigkeiten von besser als 100 kHz. Allerdings ist eine Eichung aller Linien so zu aufwendig, und es gibt nur eine begrenzte Zahl von solchen hochgenau vermessenen Linien, in der Regel in der Umgebung von wichtigen Resonanzen (z.B.He-Ne- und verdopplte Nd:YAGLaser). Vermessung solcher Linien wird z.B. von der Physikalisch-Technischen Bundesanstalt (PTB) in Braunschweig durchgeführt. Mithilfe eines Lock-in Verstärkers kann man die Ableitung einer solchen Jod-HFS Linie generieren und mit einer Rückkoppkungselektronik den Laser auf die Linienmitte stabilisieren. Dies ist in Abb. 50 gezeigt. Abbildung 50: Aufbau für die Jodsättigungsspektroskopie und die Stabilisierung des Farbstofflasers auf die Jodlinie. Quelle: Diplomarbeit Stefan Dickopf, Mainz 1993. 48 Abbildung 51: Jodspektroskopie, im oberen Teil sieht man ein dopplerverbreitertes Jodspektrum über 15 GHz und Etalonfrequenzmarker. Im unteren Bild ist eine Linie herausvergrößert und das Sättigungsspektrum (Lock-in) gezeigt. Quelle: Diplomarbeit Ines Hoog, Mainz 1991. 49 3.5.2 Zweiphotonenspektroskopie ..... Resonante und nichtresonante Zweiphotonenanregungen sind in Abb. 52 dargestellt. Der Übergang 2 2 hν2 i2 i1 hν i v realer Zwischenzustand `virtueller' Zwischenzustand hν1 hν 1 1 (b) (a) Abbildung 52: Schema eines resonanten (a) und eines nichtresonanten (b) Zweiphotonenübergangs. 1 → 2 ist für E1-Einphotonenanregungen verboten (die Parität von 1 und 2 ist identisch, die intrinsische Parität eines einzelnen Photons ist aber negativ). Es gebe nun, energetisch durchaus weit entfernte Niveaus in mit geeigneter Parität, so daß E1-Übergänge 1 → in , 2 → in erlaubt sind (z.B. wenn 1 und 2 s-Zustände sind und in p-Zustände). Treffen nun die Photonen h̄ω1 und h̄ω2 innerhalb eines ausreichend kurzen Zeitintervalls ∆t am Atom ein, so daß aufgrund der Unschärferelation ∆E ≈ h̄ ≥ |Ein − Ev |, ∆t dann kann das Atom quasi durch einen ‘Umweg’ über in von 1 nach 2 gelangen. Diese zweistufige, nichtresonante Anregung wurde erstmals 1931 von Maria Göppert-Mayer quantenmechanisch in Störungsrechnung zweiter Ordnung angegeben. Experimentell verlangt die ‘Gleichzeitigkeit’ der beiden Photonen sehr hohe Photonenflüsse, so daß Zweiphotonenspektroskopie erst 1961, gleich nach Erfindung des Lasers, realisiert wurde. Quantenmechanische Übergangswahrscheinlichkeit (ohne Herleitung, für eine detaillierte Darstellung siehe B. Cagnac et al., Journal de Physique 34, 845 (1973)): W12 ≈ γ2 I1 I2 (ω12 − (ω1 + v · k1 ) − (ω2 + v · k2 ))2 + γ22 /4 2 X < ψ |r · |ψ >< ψ |r · |ψ > < ψ2 |r · 2 |ψin >< ψin |r · 1 |ψ1 > 2 1 in in 2 1 × + . n ωn1 − ω1 − k1 · v ωn1 − ω2 − k2 · v Die Summe über n erstreckt sich über alle möglichen Zwischenzustände, oft muß man sogar Kontinuumszustände mitnehmen. Ist ein Zwischenzustand n0 besonders nahe am virtuellen Zustand, kann man näherungsweise die anderen Zwischenniveaus vernachlässigen. Da ωn0 1 − ω2 und ωn0 1 − ω1 dem Abstand ∆ωn0 zwischen virtuellem und realem Niveau n0 entsprechen, sieht man daß dann die Anregungsrate des Zweiphotonenübergangs mit 1/(∆ωn0 )2 skaliert. Der Clou bei der Zweiphotonenspektroskopie: laufen die zwei Laserstrahlen entgegengesetzt, z.B. ω1 = ω2 , k1 = −k2 , hebt sich der Dopplereffekt 1. Ordnung weg. Dies führt zum Standardaufbau der 50 Zweiphotonenspektroskopie, wie in Abb. 53 gezeigt, wo der Laserstrahl auf sich selbst rückreflektiert wird. Die Übergangswahrscheinlichkeit pro Atom ist sehr klein, da es sich um einen Prozeß zweiter Ordnung handelt, und man benötigt in der Regel sehr hohe Laserintensitäten. Die Rate skaliert mit dem Quadrat der Intensität; daher sollte die Spektroskopie im Fokus des Laserstrahls durchgeführt werden, mit Foki im Bereich von einigen zehn µm. Laser Atomstrahl k1= -k2 k1= k2 ω12 /2 ω Abbildung 53: Zweiphotonenspektroskopie, im oberen Bild ist ein typischer Aufbau gezeigt. Unten sieht man die Form des Signals: werden zwei Photonen aus entgegengesetzter Richtung absorbiert, erhält man einen dopplerfreien Peak, bei Absorption aus gleicher Richtung ergibt sich ein dopplerverbreiterter Untergrund, der jedoch bei geeigneten Polarisationen eliminiert werden kann (siehe z.B. Artikel von Cagnac oder Demtröder). Auswahlregeln: ∆L = 0, ±2, ∆π = 0. Anmerkung: die Fläche des Untergrunds sollte vergleichbar mit der des schmalen Peaks sein (genauer gesagt halb so groß) und ist hier übertrieben dargestellt. Wichtig: alle Geschwindigkeitsklassen tragen zum dopplerfreien Signal bei, bei Sättigungsspektroskopie nur ein Bruchteil ∆νn /∆νDoppler , das macht den Nachteil der geringeren Übergangswahrscheinlichkeit zumindest teilweise wieder wett. Anmerkung: in gepulsten Lasern ist natürlich die Peakintensität des Lasers sehr hoch, und Zweiphotonenspektroskopie (sowie Mehrphotonenspektroskopie) ist viel leichter durchzuführen als mit CW-Lasern. Da aber typische gepulste Laser Pulslängen von wenigen nsec aufweisen, ist ihre fourierlimitierte Frequenzbandbreite entsprechend groß, und deshalb kommen sie für Präzisionsmessungen nicht in Frage. Beispiel: Dopplerfreie Spektroskopie des 1s → 2s Übergangs in atomarem Wasserstoff (HänschGruppe, Max-Planck-Institut für Quantenoptik, München). Das Wasserstoffatom ist wegen seiner ‘simplen’ Struktur immer interessant (Test der Diractheorie, der Quantenelektrodynamik QED und in Zukunft Spektroskopie von Antiwasserstoff als Test des CPT Theorems). 51 Im feldfreien Raum lebt der 2s Zustand 0.15 sec, daher ist die natürliche Linienbreite etwa 1 Hz, und man kann am 1s → 2s Übergang sehr präzise spektroskopieren. Die chronologische Verbesserung der 1s → 2s Frequenzmessung ist in Abb. 54 gezeigt. Abbildung 54: Genauigkeit der 1s → 2s Frequenz, Quelle: Dissertation M. Niering, MPQ 2000. Das Prinzip des experimentellen Aufbaus des Münchner Experiments ist in Abb. 55 gezeigt: die Lyman-α-Wellenlänge ist 121 nm, d.h. man benötigt zwei Photonen von je 243 nm. Ein Farbstofflaser erzeugt Licht bei 486 nm, das dann in einem nichtlinearen Medium (BBO Kristall) verdoppelt wird. Abbildung 55: Schema des Münchner 1s → 2s Experiments. Das verdoppelte 243 nm Licht wird kollinear einem Wasserstoffstrahl überlagert. Um die Wechselwirkungszeit zwischen einem Atom und dem Licht zu optimieren und auch Dopplereffekte 2. Ordnung auszuschalten, wird der Wasserstoff so stark wie möglich abgekühlt. Die angeregten Atome fliegen dann durch eine Region, wo ein elektrisches Feld durch Starkmischung 2s und 2p1/2 mischt. Hier regt 52 sich das Atom in nsec unter Aussendung von Lyman-α Licht ab. Dieses Licht liefert das Detektorsignal. Die so gewonnene Resonanzkurve wird mit einem parallel mitaufgenommenen Te2 Spektrum (analog zum oben diskutierten Iod) absolut frequenzkalibriert. Darüberhinaus kann nun auch mithilfe der Frequenzkette die optische 1s → 2s Frequenz phasenkohärent mit der Cs Atomuhr verglichen werden (die Frequenzkette wird evtl. später diskutiert). Bild 56 zeigt den Einfluß der Wasserstofftemperatur auf die Linienform. Abbildung 56: Der Einfluß der Strahltemperatur auf die Linienform. Quelle: Dissertation M. Niering, MPQ 2000. Weiterhin kann man auch langsame Atome aus der Geschwindigkeitsverteilung speziell selektieren. Hierzu pulst man den Laser mithilfe eines mechanischen Choppers (siehe Abb. 55). Nach dem Blocken des Lasers durch den Chopper wartet man eine gewisse Zeit bevor man Detektorsignale registriert und verwirft somit schnelle Atome. Der Einfluß dieser Verzögerung auf die Linie ist in Abb. 57 dargestellt. Bestimmung der 1s → 2s Frequenz in Wasserstoff mithilfe der Frequenzkette und der Cs-Atomuhr lieferte die genaueste Absolutfrequenz im optischen Bereich: ν1s→2s = 2 466 061 413 187 103 (46)Hz, dies entspricht einer Präzision von 1.8 × 10−14 . Relative 1s → 2s zu 2s → 4s Messung: In der Bohrtheorie hat man die Relation ν1s→2s = 4. ν2s→4s Abweichungen entstehen durch Relativität, QED und Kerneffekte und befinden sich im GHz-Bereich. Diese Abweichungen von der Bohrschen Theorie wurden von der Münchner Gruppe auf sehr elegante Weise gemessen, wie in Abbildungen 58 und 59 illustriert. Zwei getrennte Lasersysteme werden für die Spektroskopie beider Übergänge verwendet. Befinden sich beide Laser auf der jeweiligen Resonanz, kann man die Grundfrequenz des Farbstofflasers (486 nm) mit der verdoppelten Frequenz des Titan-Saphir-Lasers (972nm/2) vergleichen, indem man beide Lichtstrahlen auf einer schnellen Photodiode überlagert, die dann Schwebungen registriert, die dem Frequenzunterschied beider Lichtwellen entspricht. Da dieser Unterschied im GHz-Bereich liegt, können diese Schwebungen elektronisch gezählt und mit der Cs-Uhr verglichen werden. Das Resultat ist eine extrem genaue Messung der Lambshift des Grundzustands. 53 Abbildung 57: Selektion von langsamen Atomen durch Flugzeitauswahl. Quelle: Dissertation M. Niering, MPQ 2000. Abbildung 58: Vergleich 1s → 2s zu 2s → 4s (I) 54 Abbildung 59: Vergleich 1s → 2s zu 2s → 4s (II) 55 4 Hochfrequenzspektroskopie 4.1 Allgemeines Hochfrequenzmethoden verwenden typischerweise Wellen im MHz bis 100 GHz Bereich. Je nach Frequenz spricht man von Radiofrequenz (RF), Hochfrequenz (HF) oder Mikrowellen. Obwohl Licht und HF Manifestationen des gleichen Phänomens, elektromagnetischen Wellen, sind, gibt es in der Praxis erhebliche Unterschiede zwischen beiden. Zum Beispiel können HF-Wellen elektronisch direkt synthetisiert werden, mit voller Phasenkontrolle. Dies führt dazu, daß HF-Generatoren als Fertiggeräte angeboten werden, in die man Frequenz, Amplitude, optionale FM oder AM Modulationen etc. digital eingibt. Abstimmbare Laser hingegen verlangen auch als kommerzielle Produkte intensive Betreuung durch einen Experten. • hνLicht ≈ eV • hν1MHz = 4 × 10−9 eV • hν1GHz = 4 × 10−6 eV Die spontane Zerfallswahrscheinlichkeit eines angeregten Zustands skaliert mit ν 3 , daher spielt im HF-Bereich, im Gegensatz zur optischen Region, spontane Emission keine Rolle. Da kT (T = 300K) ≈ 1/40 eV ist, sind z.B. die Hyperfeingrundzustände (Separation ungefähr GHz) praktisch gleichbesetzt, d.h. gewöhnliche Absorptionsspektroskopie ist nicht möglich, da der Absorptionskoeffizient ja vom Besetzungsunterschied abhängt. Dies ist auch ein Problem für Kernspinresonanzmethoden (NMR). Übergänge im HF-Bereich: • Magnetische Dipolübergänge (M1), < f |µ · B|i >, ∆π = 0. – Zeemanspektroskopie, d.h. Messung der Zeemanaufspaltung bei angelegtem Magnetfeld – Feinstruktur und Hyperfeinstruktur • Elektrische Dipolübergänge (E1), < f |eE · r|i >, ∆π = 1. – Übergänge zwischen Rydbergniveaus – Lambshift in Wasserstoff – Rotationsniveaus in Molekülen 4.2 Magnetische Dipolübergänge Einfachstes Beispiel sind die zwei Einstellungen für ein Spin-1/2 Teilchen im Magnetfeld. 1 E = gs µB Bz ms mit ms = ± . 2 D.h. im Magnetfeld sind die zwei Zustände um ∆E = gs µB Bz aufgespalten. Quantenmechanisch liegt nur µz fest. Im Vektorbild kommt dies durch die Präzession von ~µ in der x-y Ebene zum Ausdruck. 56 Elektron: ~µ = −gs µB ~s/h̄ eh̄ µB = ≈ 5.8 × 10−5 eV/Tesla 2me µB /h ≈ 14GHz/Tesla. Proton: ~ ~ K = gK µK I/h̄ µ µK = µB /1836 µK /h ≈ 7.6MHz/Tesla. Das Proton hat z.B. einen g-Faktor von 5.59. Klassisch bewirkt das Drehmoment M = µ × B die Präzession des Drehimpulses mit der Frequenz ωp = gs µB B/h̄. Damit ist h̄ωp auch die Energiedifferenz zwischen spin-up und spin-down Zustand. Die klassische Präzessionsgleichung kann für die quantenmechanischen Erwartungswerte übernommen werden: d ~ < ~s > = < ~µ > ×B dt µB ~ = −gs < ~s > ×B h̄ = ω ~ p × < ~s > . Dies ist die sogenannte Blochsche Gleichung. Der Erwartungswert < ~s > rotiert um den Präzessionsvektor ω ~ p. Bisher rotiert also < ~s > langweiligerweise um die (statische) Magnetfeldrichtung, die z-Komponente von ~s bleibt erhalten, die Präzessionsbewegung läuft in der x-y Ebene ab. Als nächstes wollen wir ein zusätzliches oszillierendes Magnetfeld einstrahlen, das z.B. die magnetische Komponente eines Hochfrequenzfeldes ist. Die folgende Betrachtung wird einfacher, wenn wir ein in der x-y Ebene rotierendes B-Feld hinzufügen (anstatt z.B. einer linearpolarisierten Welle, die sich jedoch aus solchen rotierenden Feldern aufbauen läßt): Bx = B1 cos ωt By = B1 sin ωt. Um die Blochgleichung zu lösen, erweist es sich nun als vorteilhaft, in ein mit ω ~ mitrotierendes Koordinatensystem zu gehen. Im folgenden wird klassisch gerechnet, das Resultat kann aber auf die Erwartungswerte übertragen werden. Die Darstellung folgt der von N. Ramsey [11], S. 145 ff. Im rotierenden Koordinatensystem nimmt die Blochgleichung folgende Form an: d~s ∂~s = + ω ~ × ~s, dt ∂t wobei ~s der vom stationären Beobachter gemessene Drehimpuls ist und ∂~s/∂t die vom mitrotierenden Beobachter wahrgenommene Änderung von ~s . Daraus folgt 57 ∂~s −gs µB ~ h̄ ~− ω = ~s × B ∂t h̄ gs µB gs µB ~ eff , = − ~s × B h̄ ! ~ eff = B ~ − ω~ h̄ . Das rotierende System kann nun so gewählt werden, mit dem effektiven Magnetfeld B gs µB daß in ihm das Gesamtmagnetfeld Bz = B, Bx = B1 , By = 0 ist und ω ~ = −ωẑ. Dann ist im rotierenden System das effektive Magnetfeld ~ eff = B h̄ω B0 − gs µB ! ẑ + B1 x̂, wobei B0 das ursprüngliche statische Feld ist. Die Reduktion der z-Komponente kann man anschaulich verstehen: ist ω ~ so gewählt, daß das rotierende System im ruhenden System die gleiche Rotationsrichtung hat wie die Larmorpräzession des magnetischen Moments, sieht der mitrotierende Beobachter die Präzession stark verlangsamt, nämlich mit ωp − ω; dieser modifizierten Präzessionsfrequenz ordnet er dann ein effektives Magnetfeld passender Stärke zu, entsprechend dem ersten Term in obiger Gleichung. Hinzu kommt dann natürlich noch das Wechselfeld B1 in x-Richtung. Im rotierenden System ist nun also Beff ebenfalls statisch, siehe Abbildung 60. z B0 hν/gs µB Beff θ B1 x Abbildung 60: Effektives Magnetfeld im mitrotierenden Koordinatensystem. Weiterhin gilt |Beff | = v u u t h̄ω B0 − gs µB !2 + B12 s ah̄ B1 2 = mit a = (ωp − ω)2 + (ωp ). gs µB B0 58 ~ eff ist Der Winkel θ zwischen B0 ẑ und B ωp − ω . a Für den mitrotierenden Beobachter präzediert nun das magnetische Moment um das statische Beff . Das heißt aber, daß die z-Komponente des Spins nicht länger erhalten bleibt, unter Einfluß des Wechselfeldes werden Übergänge zwischen den beiden Spinzuständen up und down induziert. cos θ = Besonders anschaulich ist dieser Effekt für ωp = ω. Dann sieht man im rotierenden System keine von B0 herstammende Präzession mehr und Beff liegt parallel zur x-Achse. Startet man in diesem Falle mit einem Ensemble von Teilchen z.B. im down-Zustand, befindet sich das Ensemble nach einer Präzession von π komplett im up-Zustand (siehe Abb. 61). Die Frequenz Ω, mit der die Spins an- und z t=π/2Ω y t=3π/4Ω Beff t=π/4Ω t=0 x Abbildung 61: Rabioszillation für ωp = ω. Zur Zeit t = 0 steht der Spin nach unten und rotiert dann in der y-z Ebene mit Kreisfrequenz Ω. abgeregt werden, heißt Rabifrequenz (nach Isidor Rabi) und beträgt auf Resonanz (ωp = ω): gs µB 2Ω0 = B1 , h̄ wobei der Faktor 2 Konvention ist 2 . Befindet sich das HF-Feld nicht genau auf Resonanz, sind die Rabiflops nicht komplett, d.h. man kann das Ensemble nie ganz in den anderen Zustand pumpen. Abbildung 62 zeigt solche Rabioszillationen. Die Rabifrequenz beeinflußt man nicht durch die Frequenz der HF, sondern durch die Amplitude. Interessant sind zeitlich begrenzte HF-Pulse der Länge ∆t. Ein sog. π-Puls auf Resonanz, d.h. 2Ω0 · ∆t = π transferiert den Spin von einem Zustand in den anderen. Ein π/2-Puls hingegen produziert ausgehend von einem reinen Spinzustand eine kohärente Superposition von up und down, dies 2 Achtung, es gibt auch andere Definitionen der Rabifrequenz in der Literatur, in der quantenmechanischen Beschreibung (siehe unten) erhält man unsere (d.h. Ramsey’s) Definition, wenn man die Wechselwirkungsenergie des magnetischen Wechselfeldes B1 exp iωt mit dem magnetischen Moment durch h̄Ω exp iωt parametrisiert. 59 Abbildung 62: Rabioszillationen, im Vgl. zum Text steht κE für 2Ω und w für 2sz . Quelle: AllenEberly. ist z.B. wichtig in experimentellen Test der Quantenmechanik und in Quantencomputern. Es sollte noch erwähnt werden, daß dieser Formalismus zwar für den anschaulichen Fall des magnetischen Moments entwickelt wurde (von Felix Bloch, 1940), aber auch für beliebige andere Zweiniveausysteme angewendet werden kann. Dann muß eben die entsprechende Wechselwirkungsenergie eingesetzt werden (statt µ · B); weiterhin hat dann der Spinvektor nicht mehr eine räumliche Interpretation, seine Projektion auf die z-Achse wird dann lediglich als Indikator der Population der zwei Zustände interpretiert; dies ist der Grund für die Achsenbeschriftung in Figur 62, sie weist auf eine Anwendung mit elektrische Dipolübergängen hin. Eine extrem wichtige Anwendung von induzierten Spinflips ist die magnetische Kernspinresonanz (NMR), die in der Medizin eine wichtige Rolle spielt. Auf eine Besprechung wird verzichtet (siehe z.B. Haken und Wolf). 4.3 Übergänge im Zweiniveausystem, quantenmechanische Behandlung Diese Darstellung betont mehr die allgemeine Anwendbarkeit (M1, E1, etc.). Auch hier soll wieder der Einfluß der spontanen Emission vernachlässigt werden. Die Darstellung folgt Ramsey [11], Seite 118 ff, allerdings mit einigen zusätzlichen Erläuterungen. Die oszillierende Störung V entspricht nichtdiagonalen Matrixelementen 60 V12 = < 2|V |1 >= h̄Ω exp iωt V21 = < 1|V |2 >= h̄Ω exp −iωt V11 = V22 = 0. Um den Einfluß dieser oszillierenden Wechselwirkung mit Frequenz ω und Stärke h̄Ω auf das System herauszufinden, muß die zeitabhängige Schrödingergleichung gelöst werden. Für das Zweiniveausystem kann man eine analytische Lösung finden. ih̄ dΨ(t) = (H0 + V )Ψ(t), dt Hierbei ist H0 der Hamiltonian für das zeitunabhängige System, d.h. H0 ψ1 = E1 und H0 ψ2 = E2 . Die Wellenfunktion Ψ(t) kann als c1 (t)ψ1 + c2 (t)ψ2 angesetzt werden. Nun multipliziert man die Schrödingergleichung von links mit ψ1∗ und integriert die Gleichung über den gesamten Raum. Man erhält dann ih̄ċ1 (t) = E1 c1 (t) + h̄Ω exp (iωt) c2 (t), und wenn man das gleiche mit ψ2∗ macht ih̄ċ2 (t) = E2 c2 (t) + h̄Ω exp (−iωt) c1 (t). Anmerkung: in der allgemeinen zeitabhängigen Schrödingergleichung müsste man eigentlich zeitabhängige Funktionen Ψa (t) = ψa exp −iEa t/h̄ einsetzen. In diesem Falle würde man nicht sofort auf die beiden letzten Gleichungen kommen. Arbeitet man statt in diesem sog. Schrödingerbild im Diracbild, erhält man eine Gleichung, wo nur die Koeffizienten ca zeitabhängig sind, aber die Wellenfunktionen ψa zeitunabhängig sind. Auf Details kann hier nicht eingegangen werden, aber im Buch von Sakurai [13] wird dies ab Seite 318 ausführlich diskutiert. Für die Anfangsbedingungen c1 (0) = 1, c2 (0) = 0, d.h. mit den Atomen anfänglich im Grundzustand, erhält man als Lösung dieser zwei gekoppelten Differentialgleichungen: 1 1 ω E1 + E2 )t] c1 (t) = (i cos (Θ) sin ( at) + cos ( at)) exp [i( − 2 2 2 2h̄ 1 −ω E1 + E2 c2 (t) = i sin (Θ) sin ( at) exp [i( − )t] 2 2 2h̄ ω0 − ω cos Θ = a 2Ω sin Θ = − q a a = (ω0 − ω)2 + 4Ω2 E2 − E1 ω0 = h̄ Aus dieser Lösung erhält man die Übergangswahrscheinlichkeit P1→2 = |c2 (t)|2 = q 4Ω2 2 1 sin (ω0 − ω)2 + 4Ω2 t . (ω0 − ω)2 + 4Ω2 2 In Abhänigkeit von der Zeit erhält man Rabioszillationen, wie in 62 gezeigt. Die Abhängigkeit von der HF-Frequenz ω ist in Abb. 63 gezeigt. 61 Abbildung 63: Linienform der Rabilösung; die Rabifrequenz Ω ist hier als b bezeichnet. Quelle: Ramsey. 4.4 Bestimmung von Kernmomenten mit dem Rabischen Apparat Mit der Stern-Gerlach Apparatur kann man das magnetische Moment von Atomen durch Ablenkung im Magnetfeldgradienten messen. Ein großes Problem hierbei ist, daß die Geschwindigkeitsverteilung zu unterschiedlichen Ablenkungen führt. Deshalb ging I. Rabi in den 30er Jahren zu Momentmessungen mit Resonanzmethoden über. Dazu verwendete er den berühmten Aufbau mit den A,B und C Magneten, wie in Abbildung 64 dargestellt ist. Abbildung 64: Rabischer Apparat zur Messung von Kern- (und Atom) Momenten. Quelle: Bergmann-Schäfer. Magnete A und B sind im wesentlichen Stern-Gerlach Magnete, jedoch mit entgegengesetztem Feld62 gradienten. Läßt man C zunächst aus, werden die Atome in A abgelenkt und dann in B wieder auf einen Detektor refokussiert, unabhängig von der Teilchengeschwindigkeit. Ein in C angelegtes homogenes Feld ändert dies nicht. Induziert man jedoch mit einem Wechselfeld in der C Region einen Spinflip, lenkt B das Atom in die gleiche Richtung wie A weiter ab und das Signal verschwindet vom Detektor (flop-out Methode). Dies geschieht nur, wenn die HF sich in Resonanz mit der Hyperfeinaufspaltung und/oder Zeemanaufspaltung in C befindet. Anwendung auf Atome mit Kernspin, aber ohne elektronischen Spin, z.B. I = 1/2: ~ E±1/2 = −~µI · B µI = − mI Bc I µI ω0 = Bc , h̄I wobei Bc das homogene Feld in C und ω0 die Resonanzfrequenz zum Umklappen des Spins ist. So kann man bei bekanntem Kernspin I das magnetische Moment messen, natürlich muß dabei auch Bc entsprechend genau bekannt sein. Die optimale Linienform dieser Resonanz hat man bei Einstrahlung eines π-Pulses (2Ω∆t = π), aber Ω sollte möglichst klein sein, da hiervon die Breite abhängt (siehe Abb. 63); folglich möchte man eine möglichst lange Wechselwirkungszeit ∆t mit der HF. Im Strahlapparat ist ∆t = lWW /vatom . Zum einen ist die Wechselwirkungszeit für einen thermischen Strahl nicht eindeutig definiert, und zudem bereitet es Schwierigkeiten, Bc über große Wechselwirkungslängen lWW homogen zu halten, dies ist typischerweise der begrenzende Faktor für die Linienbreite im Rabischen Apparat. 4.5 Methode der separierten oszillierenden Felder Diese Methode wurde von Norman Ramsey 1949 vorgeschlagen (Nobelpreis 1989). Abbildung 65 zeigt den Aufbau und das Prinzip. Am Anfang und am Ende der Sektion C sind zwei kurze HFRegionen, die phasensynchron betrieben werden. Nun wähle man z.B. in A die Projektion spin-up. Bei geeigneter HF-Intensität gibt man dann in HF1 einen π/2-Puls auf das Atom, der den Spin in die x-y Ebene klappt, wo er dann in Sektion C im Feld Bc präzediert. In HF2 wird dann wieder ein π/2-Puls eingestrahlt. Dieser vollendet den Spinflip nach down, wenn die HF-Frequenz der mittleren Larmorfrequenz ω̄L in C entspricht, weil dann die Phase der HF und des Spins während des Fluges durch C synchron bleiben. Bei allen anderen Phasen zwischen Spin und HF ist der Flip unvollständig. Der wesentliche Punkt ist, daß nur das Mittel des homogenen Feldes eingeht, d.h. man kann lWW viel länger machen als im Rabiapparat. Im Prinzip erhält man auch Spinflips, wenn sich die Phase der Larmorpräzession beim Eintritt in HF2 um 2π oder ein Mehrfaches von der HF-Phase unterscheidet. Allerdings sind diese Phasen dann geschwindigkeitsabhängig. In Figur 66 sieht man eine experimentelle Resonanzkurve, in Bild 67 theoretische Kurven. Es ist noch anzumerken, daß selbst für den Fall eines perfekt homogenen CMagneten die Breite des zentralen Peaks 40 % schmaler ist als im Rabiapparat. Die Ramseysche Methode hat große Bedeutung erlangt, z.B. in der Cäsium- Atomuhr (siehe unten). In Abb. 68 ist noch illustriert, daß man den Ramseyschen Apparat als Interferometer betrachten kann. 4.6 Messungen der Hyperfeinstruktur, Prinzip der Atomuhr Die Hyperfeinaufspaltung atomarer Niveaus kommt durch die Wechselwirkung zwischen Kernmoment und elektronischem Bahn- und Spinmoment zustande. 63 HF1 HF2 A B C HF Generator z z µ y z y x z y x x y x Abbildung 65: Ramseysche Apparatur. Im unter Teil wird das Prinzip erläutert: ein π/2-Puls in HF1 klappt den Spin auf die x-Achse, dann rotiert er frei in der C-Zone, waren die Phasen von HF und Spinpräzession synchron, klappt der zweite π/2-Puls in HF2 den Spin vollends nach unten, bei z.B. π Phasenunterschied findet kein Flip statt (gestrichelte Pfeile). Abbildung 66: Experimentell gemessene Resonanz im Ramseyschen Apparat. Quelle: Ramsey. Im Falle von Cäsium haben wir im Grundzustand 6s1/2 : l = 0, s = 1/2, I = 7/2 I und J koppeln zu einer neuen Quantenzahl F. 64 Abbildung 67: Theoretische Linienformen im Ramseyschen Apparat. Quelle: Ramsey. HF2 HF1 |2> Weg b |1> Weg a |2> |1> Abbildung 68: Der Ramseysche Apparat als Interferometer. Der erste π/2-Puls schafft eine Superposition von beiden Zuständen, die dann in HF2 wieder zusammengeführt werden. Da die beiden Zustände in C unterschiedliche Wechselwirkungsenergien haben, evolvieren ihre Phasen unterschiedlich, und am Ausgang beobachtet man deswegen ein frequenzabhängiges Interferenzmuster, wie in obigem Bild gezeigt. HHFS = C (I · J), h̄2 dies führt zu einer Hyperfeinaufspaltung ohne externe Felder von ∆EHFS = C (F (F + 1) − I(I + 1) − J(J + 1)), 2 C ist die Hyperfeinkonstante und wird experimentell bestimmt durch C = ∆E(F + 1) − ∆E(F ) . F +1 65 In Cäsium hat man im Grundzustand F = 3 und F = 4 und eine Hyperfeinaufspaltung von 9192.6 MHz. Diese Aufspaltung definiert die Sekunde. Bei keinem oder schwachem externen Magnetfeld ist F eine gute Quantenzahl, d.h. im Vektorbild addiert man I und J vektoriell auf und läßt dann den resultierenden Vektor F um B präzedieren. Legt man starke äußere Felder an, wird die Wechselwirkung zwischen J und B größer als die Hyperfeinwechselwirkung, und I und J koppeln jeweils separat an das externe Feld an. Zwischen diesen beiden Extremfällen gibt es einen Zwischenbereich, wo die Zeemanaufspaltung nichttrivial verläuft. Abbildung 69 zeigt dies für I = 3/2, also z.B. Natrium. Abbildung 69: Breit-Rabi Formel, x ist definiert als (gJ − gI∗ )µB B/∆EHFS , wobei gI∗ der g-Faktor des Kerns bzgl. des Bohrschen Magnetons ist. Quelle: Bergmann-Schäfer. Atomuhr Die Messung der Cs-Hyperfeinaufspaltung im Ramseyschen Apparat wird zur Definition der Sekunde benutzt. Abbildung 70 zeigt den Aufbau. Heutzutage ist es simpler, die Zustandsselektion und Detektion statt mit den A und B Magneten mit Lasern durchzuführen, wie in Abb. 71 gezeigt. Bild 72 demonstriert, daß man separierte Felder auch anders implementieren kann. Zuerst sind die Atome in einer Falle gefangen, dann werden sie durch einen Laserpuls von unten wie in einer Springbrunnenfontäne nach oben gedrückt, dabei fliegen sie durch eine Mikrowellenkavität. Durch die Gravitation werden die Atome dann zum Umkehren gebracht und fliegen auf dem Weg nach unten nochmals durch die gleiche Kavität. Die neuesten Atomuhren sind auf diese Weise implementiert und sind noch genauer als die alten Atomstrahluhren (siehe Abb. 73). Zum Schluß soll noch eine andere interessante, und auch oft verwendete Atomuhr gezeigt werden, der Wasserstoffmaser in Bild 74. Während bei der Cs-Uhr der Hyperfeinübergang durch externe Felder induziert wird, arbeitet der Wasserstoffmaser quasi von alleine. Ein Stern-Gerlach-Magnet selektiert den höherliegenden F = 1 Zustand und der resultierende Strahl läuft in eine Zelle, die z.B. mit 66 Abbildung 70: Prinzip der Cäsiumatomstrahluhr. Quelle: Scientific American. Abbildung 71: Cäsiumatomstrahluhr mit optischer Zustandsselektion und -detektion. Quelle: Scientific American. 67 Abbildung 72: Cs-Uhr mit lasergekühlten Atomen, eine sog. fountain clock. Quelle: Scientific American. Teflon ausgekleidet ist, um Spinflips an den Wänden zu verhindern. Zwar ist der F = 1 Zustand im Prinzip extrem langlebig. Analog zum Laser reichen aber einige wenige spontane Photonen bei 1420 MHz, um im der Resonatorkavität, die das Gefäß umgibt, durch stimulierte Emission eine Lawine loszusetzen. D.h. es bildet sich von selber ein HF-Feld in der Kavität, gespeist von den F = 1 Atomen. Eine kleine Antenne koppelt einen Bruchteil dieser Leistung aus, die Frequenz wird elektronisch gezählt. 68 Abbildung 73: Genauigkeit der amerikanischen Atomuhren am NBS/NIST. Abbildung 74: Prinzip des Wasserstoffmasers. Quelle: Scientific American. 69 5 Fallen und Kühlung für neutrale Atome 5.1 Einführung Atomstrahlmethoden: - hohe Atomgeschwindigkeiten, vw ≈ 200 − 1000 m/s, d.h. typische Wechselwirkungszeiten im Apparat liegen unter 1 ms - ineffizient - präzisionslimitierend, z.B. bei der Ramseyschen Methode Gaszellen: + lange Aufbewahrungszeiten (z.B. Wasserstoff in Teflongefäß) - Wandstöße und Stöße mit anderen Atomen stören das Atom, löschen z.B. die Phase - voller Dopplereffekt Die ideale Kombination wäre eine Falle, die die Atome im Vakuum ohne Wandkontakte festhalten kann und in der man die Atome auch abkühlen kann. Drei Grundmethoden werden hierzu verwendet: Spontane Lichtstreuung Historisch hat O. Frisch als erster die Messung des Lichtdrucks auf einen Na-Atomstrahl gemessen (Zeitschrift f. Physik 86, 42 (1933)). Die Ablenkung war mit einem hundertstel mm winzig. Das Prinzip der spontanen Lichtkraft ist in Abb. 75 gezeigt: das gerichtete Licht eines Lasers (damals Lampe) überträgt bei jeder Anregung den Impuls h̄k auf das Atom. Regt sich das Atom vorwiegend spontan ab, geht die Abstrahlung isotrop vonstatten, d.h. der Nettoimpuls des abgestrahlten Lichts summiert sich zu Null. Für jedes gestreute Photon erfährt das Atom einen Impulsübertrag von h̄k. Durch die spontante Emission hat diese Kraft dissipativen Charakter. Da aber atomare Linien wegen des Effekts der stimulierten Emission in ihrer Absorptions- und Streufähigkeit sättigbar sind, ist dieser spontanen Kraft leider eine obere Grenze gesetzt. hk Na Abbildung 75: Prinzip der spontanen Lichtkraft. Die kollimierten Photonen kommen aus der Lichtquelle, die gestreuten Photonen gehen in alle Richtungen. 70 Kraft durch einen Lichtintensitätsgradienten Letokhov hat 1968 vorgeschlagen, Atome in den Bäuchen einer optischen Stehwelle zu fangen, wobei das Licht nicht resonant ist, d.h. keine Photonen absorbiert werden. Dieser Effekt wird weiter unten diskutiert. Hier sei nur erwähnt, daß diese Kraft extrem schwach und nichtdissipativ ist, d.h. das Teilchen wird nicht gekühlt. Experimentell wurde diese Methode erst 1986 durch S. Chu in einer Falle genutzt. ~ zwischen einem externen Magnetfeld und dem atomaren Magnetkräfte Die Wechselwirkung ~µ · B magnetischen Moment resultiert in einer Kraft auf das Atom, die auch für den Bau einer Falle genutzt werden kann. Auch hier ist die Kraft sehr klein und keine Dissipation vorhanden. Die technischen Voraussetzungen für Fallen basierend auf den beiden letztgenannten Methoden waren schon lange vor der ersten erfolgreichen Atomfalle (1986) gegeben. Aber diese Fallen haben ein sehr flaches Potential, entsprechend Temperaturen kleiner als einige mK. Daher sind solche Fallen mit konventionellen Atomstrahlen nicht zu laden. Man braucht zuerst eine kühlende, dissipative Kraft, die ein Ensemble von Atomen auf entsprechende Temperaturen vorkühlt. 5.2 Formale Probleme bei der Fallenkonstruktion Beim Konzipieren einer Falle wird man mit diversen Problemen konfrontiert. Die Maxwell-Gleichungen schränken die möglichen Konfigurationen von externen Feldern (statisch und dynamisch) erheblich ein. Earnshaw-Theorem Dieses Theorem besagt, daß es unmöglich ist, Ladungen so zu plazieren, daß in einer ladungsfreien Region ein stabiler Gleichgewichtspunkt entsteht. Beweis: sei φ das Potential des Ladungsarrangements. Dann erfüllt dieses Potential im ladungsfreien Raum die LaplaceGleichung: ∆φ = 0. Für eine Funktion, die die Laplace-Gleichung erfüllt, ist aber der Funktionswert an einem beliebigen Punkt P gleich dem Mittelwert der Funktion auf einer Kugel um P . Also kann P kein Extrempunkt sein und φ kein Extremum haben, und die Wechselwirkungsenergie U = eφ kein Minimum. “No-field-maximum”-Theorem kales Maximum haben. Im ladungs- und stromfreien Raum können |E| und |B| kein lo- Allerdings kann man lokale Minima von |E| und |B| erzeugen, z.B. im Quadrupolfeld einer Antihelmholtzspule (d.h. Stromfluß in entgegengesetzte Richtung in den Spulen): dort hat man einen Punkt mit B = 0 genau im Zentrum zwischen den Spulen. Hieraus folgt dann wieder, daß man neutrale Atome nicht mit statischen elektrischen Feldern fangen kann, da man nur induzierte elektrische Dipole zur Verfügung hat, und diese sind parallel zum extern angelegten Feld. Deshalb wird die Wechselwirkungsenergie W = −dind · E nur im Maximum von |E| minimal. Anzumerken ist, daß dies nicht für Moleküle gilt, die permanente elektrische Dipolmomente besitzen können. Hingegen kann das magnetische Moment des Atoms antiparallel zum Magnetfeld eingestellt werden, indem man z.B. das geeignete mF im Stern-Gerlach-Apparat oder durch optisches Pumpen auswählt. 71 Ist das magnetische Moment dann antiparallel zum Magnetfeld, wird die Wechselwirkungsenergie im Feldminimum minimiert. Atomare Zustände mit mF dieser Art heißen weak-field-seeker. Mit diesem Effekt kann man sofort eine Falle aufbauen, wie in Abbildung 76 gezeigt. Das Problem bei einer solchen Falle ist, daß das magnetische Moment des Atoms bei seiner Bewegung durch die Falle immer der lokalen Magnetfeldrichtung adiabatisch folgen muß. W µ || Β µ || Β J=1/2 B µ || Β x µ || Β Abbildung 76: Magnetische Falle. In dieser eindimensionalen Version müßte jedes gefangene Atom beim Hin- und Herpendeln in der Falle durch die magnetische Null laufen und potentiell einen Spinflip in den antigebundenen Zustand erleiden. In zwei- und dreidimensionalen Fallen gehen aber die meisten Trajektorien genügend weit am Nullpunkt vorbei. Hat man eine Feldkonfiguration mit Nullpunkt in der Mitte, ist dieses adiabatische Folgen in einer genügend kleinen Umgebung um die Null nicht mehr gewährleistet, da sich dort die Feldrichtung örtlich sehr schnell ändert. Das Resultat sind Spinflips im Zentrum der Falle, das Atom wird vom weakzum strong-field- seeker und spürt dann ein Antifallenpotential. Insgesamt hat man mit zusätzlichen Wechselfeldern mehr Optionen. 5.3 Der Weg zur magneto-optischen Falle, Laserkühlung Laserkühlung von Atomen Wir gehen wieder vom Zweiniveauatom aus. Der Laser sei bezüglich des atomaren Übergangs ω12 um wenige Linienbreiten rotverschoben, d.h. ∆ω = ωL − ω12 ≈ −Γ. Betrachten wir nun ein Atom, das die Laserstrahlung von beiden Seiten sieht, wie in Abbildung 77 gezeigt. Bewegt sich das Atom z.B. nach rechts, sieht es Strahl 2 durch den Dopplereffekt blauverschoben, Strahl 1 rotverschoben. Damit ist das Atom mit Strahl 2 stärker in Resonanz und streut Photonen vorwiegend aus Strahl 2, erhält also einen Impulsübertrag entgegengesetzt seiner eigenen Bewegung, es wird abgebremst. Das Atom wird mithilfe des Dopplereffekts lasergekühlt. Dieses Schema kann leicht auf drei Dimensionen verallgemeinert werden, in dem man drei Paare jeweils senkrecht einstrahlt. Dieser Aufbau heißt optische Melasse, und wurde 1985 von S. Chu (Nobelpreis 1997) in den Bell-Labs realisiert (siehe Abb. 78). Wird das Atom langsamer, wird der Streuratenunterschied zwischen den 6 Strahlen immer kleiner und man erreicht ein Kühllimit bei kTDoppler = h̄Γ 2 Die Lebensdauer eines kalten Atoms (das Dopplerlimit bei Cs entspricht etwa 120µK) ist bestimmt durch Stöße mit warmem Hintergrundgas. Solche Atome (T ≈ 300 K) sind so schnell, daß praktisch 72 2 ωL 1 v 1 ωL 2 ωL Abbildung 77: Prinzip der Dopplerkühlung. Abbildung 78: Optische Melasse, im Kreuzungspunkt der 6 Strahlen leuchten die gekühlten Atome extrem hell. Quelle: Spektrum Sonderheft “Anwendungen des Lasers”. jede Kollision mit einem kalten Atom zu dessen Verlust aus der Melasse führt. Bei 10−9 mbar Vakuum kann man nur mit einer knappen Sekunde Aufenthaltsdauer in der Melasse rechnen. Optische Melasse übt eine geschwindigkeitsabhängige, aber ortunabhängige Kraft aus, deshalb ist die Dichte der Melasse relativ gering. Jetzt soll eine ortsabhängige Kraft hinzugefügt werden, um eine echte Falle zu konstruieren. 73 Ausnutzung der Lichtpolarisation Das Prinzip der magneto- optischen Falle wird am besten direkt an einem Bild erläutert (Abb. 79): Von links und rechts wird nun Licht unterschiedlicher zirkularer Polarisation eingestrahlt, z.B. σ + von links und σ − von rechts (Anmerkung: in der Atomphysik wird die zirkulare Polarisation als die Projektion des Photonenspins auf eine global definierte Quantisierungsachse definiert. Nimmt man die z.B. in der Teilchenphysik übliche Definition der Händigkeit als Projektion des Spins bzgl. des linearen Impulses des Photons, hätten in diesem Bild beide Photonen die gleiche Händigkeit). Gleichzeitig wird ein Magnetfeldgradient angelegt, der im Falle des hier gezeigten J = 0 → J = 1 Atoms den angeregten Zustand ortsabhängig aufspaltet. Der nach wie vor rotverstimmte Laser ist auf der rechten Seite mehr in Resonanz mit dem J = 0, m = 0 → J = 1, m = −1 Übergang, dieser wird aber von σ − Licht getrieben, das von rechts kommt, analog wird ein Teilchen auf der linken Seite nach rechts gedrückt, d.h. immer zum Punkt B = 0, der zur Fallenmitte wird. Gleichzeitig ist der Laser aber immer noch netto rotverstimmt, die Dopplerkühlung findet also auch noch statt. Also haben wir jetzt Orts- und Geschwindigkeitsabhängigkeit. ω 1 1 0 -1 ω Laser σ+ σ− B 0 x J 0 m Abbildung 79: Prinzip der eindimensionalen magneto-optischen Falle MOT. Quelle: Doktorarbeit, G. Gwinner, Stony Brook, NY 1995. Im Falle dieser magneto-optischen Falle (MOT) ist es nicht so klar wie bei der Melasse, daß eine Verallgemeinerung auf drei Dimensionen klappt, da man die Polarisation berücksichtigen muß. Experimentell wurde dies aber eindrucksvoll 1987 von S. Chu und D. Pritchard (MIT) demonstriert (Phys.Rev.Lett 59, 2631 (1987)). Ursprünglich kam die Idee von Jean Dalibard der Ecole Normale Superieure in Paris. Bedingt durch ihren relative großen Einfangbereich und die Kühlung ist die MOT der Ausgangspunkt für praktisch alle Fallenexperimente. 74 Quantitative Betrachtung in einer Dimension Die Kraft auf ein Atom in der MOT läßt sich für den Fall schwacher Sättigung angegen als: ∆p ∆t S0 S0 h̄kΓ − = 4(∆ω−~k·~v −βx)2 4(∆ω+~k·~v +βx)2 2 1 + S0 + 1 + S0 + Γ2 Γ2 FMOT = Der Faktor vor der Klammer stellt die Kraft auf das Atom auf Resonanz dar, entsprechend einer Streurate eines Photons alle 2 spontane Lebensdauern, d.h. bei Sättigung = 1. In der Klammer stehen die Beiträge von den zwei Lasern. Die Lorentzprofile entsprechen denen aus dem Kapitel über Sättigungsverbreiterung, sie sind ergänzt durch den Einfluß des Doppler- und Zeemaneffekts auf das Detuning, d.h. ∆ω → ∆ω ± ~k · ~v ± βx, wobei βx den Zeemaneffekt im räumlich konstanten Magnetfeldgradienten repräsentiert. Es ist noch anzumerken, daß man für schwache Sättigung, d.h. S0 < 1 die Nenner entwickeln kann und in dieser Näherung das Fallenpotential der MOT einem gedämpften harmonischen Oszillator entspricht. Nun muß noch ein optimales Detuning des Lasers und der Magnetfeldgradient gefunden werden. Ist ∆ω zu groß, werden zu wenig Photonen gestreut, und die Lichtkraft ist schwach. Ist es zu klein, können Atome mit großer Anfangsgeschwindigkeit nicht erreicht werden. Typischerweise verwendet man ein Detuning von ein bis zwei natürlichen Linienbreiten Γ und einen Gradienten von etwa 10 Gauß/cm. Eine weitere Bedingung zum Einfang schneller Atome ist, daß die Durchflugstrecke lang genug zum Abstoppen sein muß, ehe das Atom die MOT wieder verläßt. Daraus ergibt sich die Forderung nach großen Laserstrahlen und hoher Laserintensität. Als Beispiel ist in Abb. 80 die Dopplerkraft für das schwerste Alkali Francium gezeigt. In Figur 81 ist der Bruchteil der einfangbaren Atome in einer thermischen Verteilung in Abhängigkeit von der maximalen Falleneinfangsgeschwindigkeit gezeigt. Generell kann man nur einen sehr kleinen Bruchteil mit der MOT erreichen. Typische Daten einer MOT • Zahl der gefangenen Atome: bis zu 1010 , typisch 106 , aber auch einzelne Atome können beobachtet werden. • Teilchendichte ρ < 1011 cm−3 . • Durchmesser der Falle: sub-mm bis 1 cm, je nach Zahl der geladenen Atome. • Temperatur der Atome: TDoppler ≈ 100µK. • Kollisionsbedingte Lebensdauer in der Falle: 1 sec bei 10−8 mbar Vakuum bis Stunden bei 10−12 mbar. Lädt man zuviele Atome, sinkt die Lebensdauer jedoch durch falleninterne Stöße. • Atomsorten: alle Alkalis, ansonsten noch Edelgase in metastabilen Zuständen, einige Erdalkalis, leider ist Wasserstoff wegen der Wellenlänge kaum zu machen. Siehe auch www.mpihd.mpg.de/ato/lasercool/atomtraps.html. 75 2 Acceleration ][m/s 80000 D=-G D=-2G D=-G/2 40000 D=-G/10 0 -40000 -80000 -25 -20 -15 -10 -5 0 5 10 15 20 25 Velocity [m/s] Fraction of atoms below v Abbildung 80: Kühlkraft, bzw. die daraus resultierende Beschleunigung(in m/s2 ), für Francium. Zum einen sind die Beschleunigungen enorm, zum anderen ist der Fangbereich von etwa 10 m/s sehr klein zur typischen Geschwindigkeit im Franciumatomstrahl (200 m/s). Quelle: fehlerhaftes Postscriptfile von G. Gwinner, ca. 1995. Lehre: Fonts immer im Dokument mit abspeichern. 0 10 -1 10 -2 10 -3 10 -4 10 -5 10 -1 0 10 10 v/v thermal Abbildung 81: Bruchteil der einfangenen Atome als Funktion der maximalen Fanggeschwindigkeit v der MOT. Zwei der stärksten MOTs, S. Chus Cs-MOT und die Fr-Falle des Autors, erreichen Fanggeschwindigkeiten von v/vw ≈ 0.2. Selbst in diesem Fall kann man nur etwa 1/200 aller Atome erreichen. Diodenlaserbetriebene Fallen haben in der Regel v/vw < 0.1. Quelle: G. Gwinner, ca. 1995. Anmerkung: bald nach der Erfindung der MOT wurde festgestellt, daß die gemessenen Temperaturen in der Falle deutlich unter dem von der Dopplertheorie vorhergesagten Limit lagen, zumindest bei Cs und Na; hier fand man Temperaturen deutlich unter 100µK. Dies ist einer der (leider) seltenen Fälle, wo man mehr bekommt als man ursprünglich wollte. Die Erklärung dieser kälteren Temperaturen hat mit Lichtpolarisationsgradienten in der Falle zu tun und sprengt den Rahmen dieser Ausführung, Details findet man z.B. in [14]. 76 Abbildung 82: Photo einer Na-MOT am NIST, Washington DC aus der Gruppe von W.D. Philips (Nobelpreis 1997). 5.4 Einige technische Details zur MOT Der Rückpumper Um eine große spontane Kühlkraft zu erhalten, muß man einen geschlossenen Übergang wählen, wie er im Zweiniveauatom per Definition natürlich immer vorhanden ist. “Echte” Atome sind komplizierter, und schon das Vorhandensein einer Grundzustandshyperfeinaufspaltung (bei Alkalis immer) schafft Probleme, die aber relativ leicht zu lösen sind. Abbildung 83 illustriert dies im Falle von 87 Rb. Der Übergang 2 → 3 ist fast geschlossen, da durch die Auswahlregel ∆F = 0, ±1 der angeregte F = 3 Zustand in den Ausgangszustand F = 2 zurückzerfallen muß. Bedingt durch die Linienbreite im Atom und des Lasers kann es aber gelegentlich passieren, daß man 2 → 2 anregt, dann ist aber ein Zerfall in den F = 1 Grundzustand möglich, das Atom wird dunkelgepumpt. Legt man aber nun einen “Rückpumplaser” auf 1 → 2, werden diese Atome dem 2 → 3-Zyklus wieder zugeführt. Effizientes Laden • Abbremsung eines Atomstrahls mit einem “Zeeman-Slower” (siehe Abb. 84). Dem Atomstrahl läuft ein Laserstrahl entgegen. Um ihn während des Abbremsens in Resonanz mit den langsamerwerdenden Atomen zu halten, wird die atomare Resonanz in einem konischen Solenoid mithilfe des Zeemaneffekts entlang der Flugstrecke variiert. Für Natrium ist ein Zeeman-Slower etwa 80 cm lang. • Dampfzellen-MOT: die MOT befindet sich innerhalb einer Dampfzelle, die mit einem Dampf des gewünschten Elements gefüllt wird (p < 10−8 mbar). Die MOT fängt dann die Atome, die in der Maxwell-Boltzmann-Verteilung unterhalb der Einfangsgeschwindigkeit liegen. Diese Atome werden also dem Dampf entzogen, der Rest wird durch Stöße wieder in eine M-BVerteilung evolvieren, von der wieder die langsamen Atome abgezapft werden können. 77 F 3 267 MHz 2 5p3/2 157 MHz 1 72 MHz 0 Rückpumper (schwach) Kühllaser (stark) D2 Linie 780 nm 2 5s1/2 6 GHz 1 Abbildung 83: Prinzip des Rückpumplasers. Abbildung 84: Das Prinzip des Zeeman-Slowers. Quelle: Spektrum Sonderheft “Anwendungen des Lasers”. 78 5.5 Weitere Fallen Die magneto-optische Falle hat auch gravierende Nachteile: • starke Lichtstreuung, die Atome befinden sich ständig in resonantem Licht im Bereich der Sättigung • Magnetfeldgradient, dies schließt viele Präzisionsmessungen in der MOT aus Deshalb wird die MOT oft nur zur Produktion kalter Atome eingesetzt. Zur eigentlichen Messung werden dann die Atome in andere Fallen umgeladen. 5.6 Optische Dipolfallen Dieser Fallentyp wurde zuerst mit makroskopischen, dielektrischen Kügelchen realisiert (A. Ashkin, Bell Labs, 70er Jahre). Die auf das Kügelchen ausgeübte Kraft ist anschaulich verständlich und das Prinzip ist in Abbildung 85 erläutert. Ein Teilchen mit einem bzgl. der Umgebung größeren Brechungsindex wird in das Intensitätsmaximum des Strahls hineingezogen. Mit einem fokussierten Strahl, wie in Abb. 85 gezeigt, kann man ein dreidimensionales, lokales Intensitätsmaximum realisieren (zur Erinnerung: dies war mit statischen elektrischen Feldern nicht möglich, hier handelt es sich jedoch um elektrische Wechselfelder). Abbildung 85: Prinzip der optischen Dipolfalle, hier wird ein lokales Intensitätsmaximum durch die Fokussierung eines Laserstrahls realisiert. Quelle: Spektrum Sonderheft Anwendungen des Lasers. 79 Abb. 86 zeigt wie ein Kügelchen (heller Punkt rechts oben) vom Laser in der Schwebe gehalten wird. Um die Adhäsion an der Küvettenoberfläche zu überwinden, werden die Kügelchen vom Boden mit einem Piezokristall losgerüttelt. Abbildung 86: Falle für ein makroskopisches Kügelchen. Quelle: Spektrum Sonderheft Anwendungen des Lasers. Anwendung der optischen Dipolfalle in der Biologie Die optische Dipolfalle hat als ’Optische Pinzette’ Einzug in die Biologie und Medizin gehalten. Dies ist in der Abbildung 87 erläutert. Optische Dipolfalle für atomare Teilchen Hier bedienen wir uns wieder des klassischen Modells der durch das elektrische Feld des Laserstrahls erzwungenen Schwingung des Elektrons. Liege die erste Anregungsfrequenz des Atoms bei ω0 . Befindet sich die Laserfrequenz unterhalb ω0 , hat man einen Phasenverschub φ zwischen Anreger (Laserfeld) und Elektron kleiner als π/2, d.h. die Wechselwirkungsenergie W = −|d||E| cos φ ist negativ, wobei d~ das induzierte Dipolmoment ist. Folglich erfährt das Atom eine Kraft in Richtung ansteigender Lichtintensität in dieser rotverschobenen Falle. Analog sind für Laserfrequenzen oberhalb von ω0 die Welle und das induzierte Dipolmoment gegenphasig, d.h. W = −|d||E| cos φ > 0, somit wird das Atom aus dem Lichtfeld in der blauverschobenen Falle herausgedrückt. Mit stark fokussierten Laserstrahlen kann man Fallentiefen entsprechend Teilchentemperaturen von etwa 1 mK erreichen, deshalb muß man optische Dipolfallen indirekt, etwa durch die MOT, laden. Das wesentliche Merkmal der Dipolfallen ist die Tatsache, daß das Licht nichtresonant ist, das heißt es daß das Atom (fast) keine Photonen streut, spontane Emission wird extrem reduziert, somit wird das Atom “in Ruhe gelassen”, im Gegensatz zur MOT, wo man einen atomaren Übergang geradzu sättigt. Deshalb sind optische Dipolfallen potentiell sehr geeignet für Präzisionsmessungen. 80 Abbildung 87: Quelle: Optische Dipolfallen, M. Weidemüller und R. Grimm, Physikalische Blätter 55, Nr. 12, 41-47 (1999). 81 Verschiedenen Typen von Dipolfallen: • FORT (far-off-resonance trap, die der Autor aus offensichtlichen Gründen gerne far-awayresonance trap genannt hätte): dies war die erste erfolreiche Dipolfalle, gebaut von D. Heinzen, U.o.Texas, Austin 1993. Hier wurden ungefähr 103 − 104 85 Rb Atome im 10 µm weiten Fokus eines 65 nm rotverstimmten Lasers gefangen. Trotz der geringen Anzahl von Atomen betrug die Dichte 1012 cm−3 , also deutlich mehr als in der MOT, die zum Laden verwendet wurde. Die Streurate für Photonen betrug lediglich 100 pro Sekunde, im Vergleich zu etwa 107 in der MOT. Zu erwähnen sei noch, daß die Fokusfallen ein sehr unterschiedliches Fallenpotential in radialer und axialer Richtung haben, da radial die Lichtintensität sehr schnell abfällt, typischerweise hat man ein Gaußprofil. • QUEST, (quasi-electrostatic trap), der Extremfall einer rotverstimmten Falle, entwickelt von R. Knize (U.o.Southern California), 1995. Hier wird ein CO2 Laser bei λ = 10.6 µm verwendet. Bei Atomen mit der niedrigsten Anregung im nahen Infrarot oder Sichtbaren führt dies zu Streuraten von weniger als 0.001 pro Sekunde! Gefangen wurden etwa eine Million Atome mit einem 20W CO2 Laser, fokussiert auf 0.1 mm (hier macht sich bereits die große Wellenlänge bemerkbar). Die Fallentiefe betrug nur 115 µK. • Blauverschobene Pyramidenfalle von S. Chu, Stanford. Mithilfe von zylindrischen Linsen wurden flache Lichtblätter (light sheets) erzeugt und gekreuzt, wie im Bild 88 gezeigt. Die Idee hier ist, daß die Atome aus dem Lichtfeld herausgedrückt werden und deshalb wenig Photonen streuen, ohne daß man so extreme Verstimmungen wie beim CO2 Laser nehmen muß. Na Atome (λ = 589 nm) wurden mit einem Ar-Laser (16 W auf den 514 un 488 nm Linien) gefangen, das Strahlprofil war 15 µm × 1 mm. Die Abstoßung entsprach einem Potential von 100 µK, etwa 3000 Atome wurden beoabachtet. • Blauverschobene Falle mit einer evaneszenten Welle. In Dipolfallen ist es offensichtlich wichtig, starke Lichtintensitätsgradienten zu verwenden. Selbst bei einem extrem fokussierten Strahl (typisch einige µm Durchmesser im Fokus) erstreckt sich der Abfall der Intensität über etliche Wellenlängen. Eine elegante Methode zur Erzeugung extrem steiler Lichtgradienten ist die Verwendung von evaneszenten Wellen: wird ein Lichtstrahl an einer Oberfläche totalreflektiert, erstreckt sich das Lichtfeld ein kleines Stück über die Oberfläche hinaus, und fällt exponentiell mit einer charakteristischen Länge von ≈ λ/2π ab. Dies ist in Abb. 89 anhand der gravitooptische Falle GOST illustriert. Die Atome werden aus der MOT fallengelassen und hüpfen dann auf der evaneszenten Welle wie auf einem Trampolin. Damit sie nicht seitlich entweichen, wird die Falle mit einem blauverstimmten Hohlstrahl umgeben, diese Anordnung ist dem in der Quantenmechanik theoretisch so viel verwendeten Kastenpotential sehr ähnlich. 5.7 Anwendung von Fallen am Beispiel der Bose-Einstein-Kondensation Wenn bosonische Teilchen mit genügend Phasenraumdichte vorliegen, so daß der Abstand zwischen den Teilchen kleiner als die de-Broglie Wellenlänge wird, d.h. die Wellen der einzelnen Teilchen überlappen, kommt es zum Phänomen der Bose-Einstein-Kondensation. Das Kondensat wird dann durch eine einzige, makroskopische Wellenfunktion beschrieben. Dies ist grafisch in Abbildung 90 dargestellt. Bisher war der BEC-Effekt nur in Helium bekannt, verknüpft mit dem Phänomen der Suprafluidität etc. Allerdings handelt es sich bei flüssigem Helium um ein stark-wechselwirkendes System, d.h. die hohe Phasenraumdichte wird erzielt mit hoher räumlicher Dichte und kurzen de-BroglieWellenlängen. Deshalb sind sich die He-Atome sehr nahe und die Beschreibung der Atom-Atom 82 Abbildung 88: Blauverstimmte invertierte Pyramidenfalle. Die V-förmigen Flächen werden von den Laserstrahlen gebildet, die Gravitation drückt die Atome von oben in die invertierte Pyramide. Quelle: H.J. Lee et al., Physical Review Letters 76, 2658 (1996). Abbildung 89: Gravito-Optische Falle GOST. Quelle: M. Weidemüller und R. Grimm, Physikalische Blätter 55, Nr. 12, 41-47 (1999). Wechselwirkung ist ungleich komplizierter als im Falle eines sehr verdünnten Gases, wo man hohe Phasenraumdichte mit großen Teilchenabständen und großen de-Brogliewellenlängen erzielt (siehe Abb. 91. Dazu braucht man natürlich ultrakalte Atome, und es war frühzeitig erkannt worden, daß Laserkühlung die beste Chance dazu bietet. In vieler Hinsicht wurde die rasante Entwicklung von Fallenmethoden in den letzten zehn Jahren vom Wettlauf zur Herstellung eines Kondensats getrieben. Für n λ3dB ≥ 2.612 besetzen alle Bosonen den gleichen, tiefsten Zustand, und es findet ein Phasenübergang statt; n ist hierbei die Teilchendichte (der genaue numerische Faktor hängt übrigens vom Fallenpotential ab), die de-Broglie Wellenlänge ist λdB = = h 1 ∝ √ mv T s 2πh̄2 mkT Am Beispiel von Natrium in einer MOT (T ≈ 20µK,n ≈ 1011 cm−3 ) kann man sich leicht überzeugen, daß man die notwendige Phasenraumdichte nicht schaffen kann, da nλ3dB ≈ 10−5 bei weitem zu klein ist. Deshalb muß man die Atome in magnetische oder optische Fallen umladen. Da diese Fallen 83 Abbildung 90: Grafische Darstellung des Kondensationsprozesses, Quelle: Webseite von W. Ketterles Gruppe am MIT, Boston. Abbildung 91: Beziehung zwischen Teilchenabstand und de-Broglie Wellenlänge für BEC. Quelle: Physikalische Blätter. jedoch konservative Potentiale nutzen, müssen zusätzliche Mechanismen zur Erhöhung der Phasenraumdichte eingesetzt werden. Der richtige Weg wurde mit dem sogenannten evaporativen Kühlen gefunden. Evaporatives Kühlen Diese Methode wird hier anhand der magnetischen Falle demonstriert. Wie in Abb. 92 gezeigt, wird Radiofrequenz der passenden Wellenlänge eingestrahlt, so daß Teilchen ab 84 einer bestimmten Energie im Fallenpotential so weit nach außen wandern können, daß die RF einen Spinflip induzieren kann. Effektive schneidet man das Potential somit bei einer bestimmten Höhe ab. µ || Β W µ || Β B µ || Β J=1/2 hνRF x µ || Β Abbildung 92: Evaporatives Kühlen in der magnetischen Falle. Die Radiofrequenz induziert Spinflips bei einer bestimmten Fallenhöhe. Die heißen Teilchen in der Falle werden also “verdampft”. Zurück bleibt ein kälteres Ensemble, das zudem noch eine höhere Dichte hat. Wichtig ist, daß man die Teilchen langsam verdampft, damit die verbleibenden Atome wieder Zeit zum Thermalisieren haben. Dazu wird die RF-Frequenz langsam abgesenkt. Dies ist in Abb. 93 verdeutlicht. Abbildung 93: Evaporatives Kühlen. Quelle: Webseite der Ertmer-Gruppe, Univ. Hannover. Wie schon weiter oben erwähnt, hat man das Problem der Spinflips im Zentrum der Falle, falls man dort ein verschwindendes Feld hat. Da das evaporative Kühlen recht langsam geht (über viele Sekunden hinweg), sind die Verluste zu hoch. Historisch wurde diese Problem zuerst mit der sog. TOP-Trap in Boulder gelöst, wo das erste Kondensat hergestellt wurde. Da dieses Prinzip technisch etwas unhandlich ist, sollen hier die moderneren Methoden vorgestellt werden. 85 • Die Atome werden optisch vom Fallenzentrum ferngehalten mit einem blauverstimmten Lichtstrahl, quasi eine Kombination von magnetischer und optischer Falle, man spricht vom optischen Propf. Das resultierende Potential ist in Abb. 94 gezeigt. • Verwendung einer magnetischen Falle ohne Magnetfeldnull, zum Beispiel die Kleeblattfalle (cloverleaf-trap), benannt nach dem Aussehen der Spulen (Abbn. 95 und 96). Abbildung 94: Verhinderung von ungewollten Spinflips im Fallenzentrum durch einen blauverstimmten Lichtstrahl. Mit diesen Methoden war es nun möglich, BEC zu produzieren. Zuerst war die Gruppe um C. Wieman und E. Cornell am JILA in Boulder/Colorado mit Rubidium erfolgreich, gleich darauf R. Hulet (Rice U./Houston) mit 7 Li, diese Messung wurde jedoch angezweifelt und erst ein Jahr später überzeugend wiederholt. Drei Monate nach der Erstentdeckung war dann auch die Gruppe von Wolfgang Ketterle am MIT mit 23 Na erfolgreich, die dann schnell die Führung auf diesem Gebiet übernahm. Das Diagramm 97 zeigt nochmals die Entwicklung der Phasenraumdichte in den Jahren der Entdeckung von BEC. Abschließend nun noch einige schöne Bilder rund um BEC: in Bild 98 sieht man die zeitliche Entwicklung eines Kondensats. Die z-Achse ist ein Maß der Anzahl der Atome in Abhänigkeit ihrer kinetischen Energie entlang der 2 Hauptachsen der Falle. Im ersten Bild sieht man die Verteilung in der Falle vor der Entstehung des Kondensats. Im zweiten Bild schießt plötzlich ein schmaler, also kalter, Peak in der Mitte heraus, der nicht einer thermischen Verteilung von Atomen entspricht — das Kondensat. Treibt man das evaporative Kühlen noch weiter, sind schließlich in Bild 3 praktisch alle Atome Teil des Kondensats. Zum Erstellen von Bild 98 war es notwendig, für jede einzelne Temperaturmessung die Falle abzuschalten und mit einer ballistischen Flugmessung die Temperatur der Atome zu bestimmen, d.h. jedesmal wird das Kondensat zerstört. Eine viel effizientere Methode der zerstörungsfreien Beobachtung der Evolution des Kondensats wurde von Ketterle eingeführt: die Phasenkontrastmethode. Ein von der atomaren Resonanz verstimmter, also wenig Photonen streuender, Laserstrahl durchläuft die 86 Abbildung 95: Layout der Kleeblattfalle. Quelle: Webseite der Ketterle-Gruppe am MIT. Abbildung 96: Feld der Kleeblattfalle. Achtung: die Abszisse zeigt B − B0 . Quelle: Webseite der Ketterle-Gruppe am MIT. Falle, erfährt aber durch die Gegenwart der Atome einen Phasenverschub (das Fallengas hat ja einen Brechungsindex der vom Vakuumwert verschieden ist). Hinter der Falle wird dieser Strahl mit einem Referenzstrahl, der nicht durch die Falle ging, überlagert und zum Interferieren gebracht. Damit kann man die Kondensatsevolution in Echtzeit beobachten, wie in Abb. 99 gezeigt. Weiterhin kann man zwei Kondensate miteinander interferieren lassen. Man erzeugt diese z.B. durch einen blauverstimmten Laserstrahl, der die ursprüngliche Falle und das Kondensat in zwei Teile spal- 87 Abbildung 97: Entwicklung der erzielten Phasenraumdichte, Quelle: Webseite der Ketterle-Gruppe am MIT. Abbildung 98: Entstehung eines Kondensats mit fortschreitendem evaporativem Kühlen. Quelle: Webseite der Ketterle-Gruppe am MIT. tet, analog zum optischen Pfropf. Dann kann man die Kondensate wieder zusammenführen und beobachtet Interferenz, wie Bild 100 bezeugt. Seit 1995 gibt es zahlreiche Gruppen, die erfolgreich BEC hergestellt haben, die BEC-Homepage an der Georgia State University enthält eine aktuelle Liste (Abb. 101). Alle Experimente verwenden die gleichen Alkaliatome wie die ersten drei Gruppen mit der Ausnahme des Wasserstoffexperiments von D. Kleppner am MIT. Mit diesem Experiment hatte in den 70ern die Suche nach BEC in atomaren Gasen angefangen. Da man für Wasserstoff keine MOT zur Verfügung hat, basierte dieser Versuch ausschließlich auf magnetischen Fallen und evaporativer Kühlung. Da Wasserstoff theoretisch viel einfacher ist als schwere Alkalis, bedarf dieses Experiment besonderer Erwähnung. Abschließend sei noch der sogenannte Atomlaser erwähnt. Reduziert man die RF-Frequenz soweit, 88 Abbildung 99: Evolution eines Kondensats beobachtet mit der Phasenkontrastmethode. Die Farbcodierung entspricht dem Phasenverschub und damit der lokalen integrierten Dichte entlang der Beobachtungsrichtung. Das Kondensat macht sich durch das Erscheinen einer sehr dichten Komponente in der Fallenmitte bemerkbar. Die Zigarrenform der Atomwolke rührt von den unterschiedlichen Potentialgradienten in axialer und radialer Richtung in der Kleeblattfalle her. Quelle: Webseite der Ketterle-Gruppe am MIT. Abbildung 100: Interferenz zweier Kondensate. Quelle: Webseite der Ketterle-Gruppe am MIT. daß auch Atome des Kondensats durch Spinflips aus der Falle gelangen, kann man damit einen kontinuierlichen, kohärenten Materiewellenstrahl auskoppeln. Ob dieser Atomlaser nun wirklich das exakte Äquivalent zum optischen Laser ist, sei an dieser Stelle dahingestellt. Mit den Bildern des gepulsten Atomlasers vom MIT (Bild 102) und des kontinuierlichen vom MPI f. Quantenoptik in München (Bild 103) ist es nun zunächst einmal mit den bunten Bildern vorbei. Neue Entwicklungen Der Rice-Gruppe gelang es, bosonisches 7 Li und auch fermionisches 6 Li in einer identischen Falle zu speichern. Abbildung 104 zeigt, daß während des evaporativen Kühlens die Wolke bosonischen Lithiums immer kleiner wird, wohingegen das Fermionengas aufgrund des Pauliprinzips am weiteren Kollaps gehindert wird (dies ist der sog. Fermidruck, der in entarteter Materie wie weissen Zwergen und Neutronensternen eine wichtige Rolle spielt, A.G. Truscott et al, “Observation of Fermi Pressure in a Gas of Trapped Atoms”, Science Express (2001) and Science 291 (2001), siehe auch http://atomcool.rice.edu/Welcome.html). 89 Abbildung 101: Entwicklung der BEC Forschung in den letzten Jahren. Quelle: GSU-Webseite http://amo.phy.gasou.edu/bec.html/. Am MPQ in München und auch hier in Heidelberg wird an Mikrofallen gearbeitet, in denen das Magnetfeld durch Ströme auf Leiterbahnen geformt wird. So erzeugt z.B. die Kombination eines extern angelegten homogenen Feldes mit den kreisförmigen Feldlinien um eine Leiterbahn ein Quadrupolfeld unmittelbar oberhalb der Oberfläche. Abb. 105 zeigt den Aufbau aus verschiedenen Perspektiven. Wechselströme mit passendem Phasenverschub durch die zwei mäandrierenden Leiterbahnen erzeugen Potentialtäler die monoton in eine Richtung laufen. Das in der Magnetfalle (links) erzeugte Kondensat wurde mit diesem “Potentialfließband” einige Millimeter transportiert. Diese Methode könnte der Ausgangspunkt für diverse neue, kompakte atomoptische Bauteile sein. 90 Abbildung 102: Gepulster Atomlaser, ausgekoppelte Teile vom Kondensat als Phasenkontrastbild. Quelle: Webseite von W. Ketterle, MIT. Abbildung 103: Kontinuierlicher Atomlaser. Quelle: Webseite der Hänsch-Gruppe am MPQ in München. 91 Abbildung 104: Verhalten von bosonischem und fermionischem Lithium während des evaporativen Kühlens. Quelle: http://atomcool.rice.edu/Welcome.html. Abbildung 105: Mikrofalle am MPQ. Das Bild rechts unten kann als Animation unter http://www.mpq.mpg.de/ jar/conveyer animation.html angeschaut werden. Quelle: MPQ München, Hänsch Gruppe. 92 6 Atomphysik mit geladenen Teilchen 6.1 Erzeugung von Elektronen-, Positronen- und Ionenstrahlen 6.1.1 Elektronen Elektronen erzeugt man typischerweise mit einer “Elektronenkanone”, im Prinzip ähnlich der Fernsehröhre. Elektronen treten aus einer Glühkathode aus und werden durch eine Abzugsspannung aus der Raumladungswolke vor der Kathodenoberfläche in einen Strahl abgezogen, wie in Abb. 106 gezeigt. Anzumerken ist hierbei, daß ein optimal kollimierter Elektronenstrahl mit der sog. PierceAnordnung erreicht wird, d.h. die Kathode ist nach außen von einer nach vorne gekippten ringförmigen Elektrode umgeben. Die Elektronenstromdichte aus einer raumladungsbegrenzten Elektronenka- Abbildung 106: Elektronenkanone und der Einfluß der Pierce- Geometrie. Quelle: Moore. none ist limitiert und ist gegeben durch U 3/2 Jmax (e ) = 2.34 2 µAcm−2 , d − wobei U das Beschleunigungspotential in Volt und d die Entfernung zwischen Kathode und Anode in cm sind. Als Strom erhält man somit − Imax (e ) = πra2 Jmax ra = 7.35 d 2 U 3/2 µA. Beispiele: • Bei 20 eV Strahlenergie kann man bei typischen Kathodengrößen einige 10 µA erwarten. 93 • Elektronenkühler am Schwerionenspeicherring TSR (MPIK Heidelberg): die Kathode hat 1 cm Durchmesser, Beschleunigungsspannungen um 5 kV werden verwendet, dabei erhält man einige hundert mA. Der Strahl befördert einige kW Leistung und muß am Ende des Kühlers abgebremst werden, bevor er auf eine Oberfläche aufkommt, sonst kann sich der Strahl leicht durch die Vakuumkammer “hindurchschweißen”. Weitere Methoden zur Erzeugung von Elektronenstrahlen sind Feldemission und Photokathoden (z.B. GaAs, hier kann man besonders bequem polarisierte und gepulste Strahlen herstellen). 6.1.2 Positronen Problem: Positronen werden hochenergetisch erzeugt, z.B. durch β + -Zerfall einer 22 Na Quelle oder durch Paarbildung an Beschleunigern, wie in Abb. 107 gezeigt. In der Atomphysik benötigt man je- Abbildung 107: Positronenproduktion mit einem Elektronenlinearbeschleuniger. Quelle: Webseite der ETL-Facility, Japan. doch in der Regel viel langsamere Positronen. Diese werden durch Positronenmoderation erzeugt. Das Prinzip der Moderation ist in Abbildung 108 gezeigt. Es beruht auf der etwas erstaunlichen Tatsache, daß ein Positron in einem Kristall wesentlich schneller durch Stöße thermalisiert wird als es einen Annihilationspartner finden kann. Wenn dann das Kristallmaterial, so wie im Falle von Wolfram und einigen anderen Metalen, noch eine negative Austrittsarbeit für Positronen hat, d.h. das Material Positronen nahe der Oberfläche quasi “ausspuckt”, kommt das thermalisierte Positron wieder ins Vakuum ehe es annihiliert. An Beschleunigern wie der ETL-Anlage in Japan oder auch Reaktoren (z.B. Garching) kann man bald mit 108 langsamen Positronen pro Sekunde rechnen. Positronenphysik • Positronen werden häufig in der Festkörper- und Oberflächenphysik benutzt. • Herstellung von Positronium (e+ e− ). Ps ist ein rein leptonisches Äquivalent zum Wasserstoffatom und eines der wichtigsten Objekte zum Studium der Quantenelektrodynamik. Momentan 94 Abbildung 108: Positronenmoderation in einer Wolframfolie. Quelle: Webseite der Positronengruppe an der Univ. Halle. interessiert insbesondere eine Diskrepanz zwischen experimenteller und gerechneter Lebensdauer des Triplett-(ortho-)Zustands von Ps (siehe Abb. 109). • In eigener Sache: derzeit findet am MPIK ein Experiment mit dem negativen Ps-Ion, also (e+ e− e− ) statt. Abb. 110 erläutert die Herstellung und den Nachweis von Ps− . Ein Positron durchläuft eine extrem dünne Kohlenstoffolie (≈ 50 Å), dabei kommt es mit einer Wahrscheinlichkeit von etwa 10−4 vor, daß das Positron zwei Elektronen mitreißt. Hinter der Folie wird das Ps− sofort auf einige kV beschleunigt. Wenn es dann nach durchschittlich 400 ps annihiliert, 95 werden im häufigsten Modus 2 511 keV Photonen ausgesandt. Beobachtet man in Vorwärtsrichtung, sieht man eines dieser Photonen um einige 10 keV blauverschoben, d.h. man kann es eindeutig von den 511 keV Photonen, die von der Annihilation “gewöhnlicher” Positronen an Oberflächen der Apparatur stammen, unterscheiden (Abb. 111). Brandaktuell wurde Ps− jetzt auch am MPIK beobachtet (Abb. 112). Abbildung 109: Lebensdauer von Orthopositronium. Abbildung 110: Produktion von Ps− . 96 Abbildung 111: Annihilationsspektrum von Ps− . Quelle: A.P. Mills, Phys.Rev.Lett 50, 671 (1983). Abbildung 112: Produktion von Ps− am MPIK, Feb. 2001. 97 6.1.3 Ionenquellen Oberflächenionisation Aufgrund ihres niedrigen Ionisationspotentials können Alkalis leicht beim Austritt aus Oberflächen ionisiert werden. Eine einfache Implementation ist in Bild 113 gezeigt. Abbildung 113: Einfache Ionenquelle für Alkaliatome, die an der Wolframoberfläche ionisiert werden. Quelle: Moore. Entladungsquellen, Duoplasmatronquelle In Entladungsquellen werden die Ionen in einer Gasentladung produziert. Die technische Herausforderung ist hierbei, die Entladung räumlich zu begrenzen und zu verdichten. Als Beispiel soll hier die Duoplasmatronquelle dienen, wie sie in Abb. 114 gezeigt ist. Hier ist ein Teil des Eisenjochs (das sog. “Zwischen”) so geformt, daß die Entladung auf das Gebiet der Öffnung in der Mitte des Zwischens begrenzt wird und sich die Ionen im “plasma cup” sammeln, wo sie vom Extraktor abgezogen werden können. Typischerweise beträgt der Gasdruck 100 mbar, die Entladung läuft mit 0.5 .. 2 A und man erhält einige mA einfach positiv geladener Ionen, auch einige µA zweifach geladener Ionen. Man kann auch negativ geladene Ionen extrahieren, was zum Beispiel für den Betrieb von Tandem Van-de-Graaff Beschleunigern sehr wichtig ist. Ionenquellen für höhere Ladungszustände: die EZR Um Ionen in höheren Ladungszuständen zu produzieren, bedient man sich z.B. der Elektron-Zyklotronresonanzquelle EZR, die in Abb. 115 gezeigt ist. Hier wird mit geeigneten Magneten (teilweise mit reinen Permanentmagneten) ein Magnetfeldminimum in der Mitte der Kammer erzeugt. Die Idee ist, daß die Elektronen das Kammerzentrum nicht verlassen können, da der Richtung Wand herrschende magn. Feldgradient zu einer magnetischen Spiegelung der Elektronen führt (siehe z.B. Jackson, Kap. 12.6). Weiterhin werden Mikrowellen auf der Zyklotronresonanzfrequenz der Elektronen eingestrahlt; die damit beschleunigten Elektronen ionisieren die Ionen, die dann extrahiert werden könne, da sie durch ihre hohe Masse nicht dem magnetischen Einschluß unterliegen. Die AECR-Quelle am 88” Zyklotron in Berkeley kann z.B. 11 mA U38+ liefern! Höchstgeladene Ionen: die EBIS Um zu den allerhöchsten Ladungszuständen zu gelangen (Stichwort “nacktes Uran”), kann man sich der “electron beam ion source” EBIS bedienen. Ihr liegt ein 98 Abbildung 114: Duoplasmatronquelle. Quelle: Moore. Abbildung 115: Elektron-Zyklotronresonanzquelle. Quelle: Salzborn-Gruppe, Univ. Giessen. hochenergetischer, fokussierter Elektronenstrahl zugrunde. In diesen wird, wie in Abb. 116 gezeigt, ein Atomstrahl eingeführt. Die schnellen Elektronen (bis hunderte von keV) ionisieren dann in Stößen die Ionen zu immer höheren Ladungszuständen. Dazu ist es notwendig, daß die Ionen genügend lang im Elektronenstrahl verweilen. Deshalb wird während des Ladungszustandsbrütens auf beiden Seiten ein abstoßendes Potential angelegt, das die Ionen axial einschließt. Der radiale Einschluß erfolgt durch das Raumladungspotential des Elektronenstrahls, das für die positiv geladenen Ionen in der Mitte des Elektronenstrahls ein Minimum hat. Deshalb kann diese Apparatur auch als EBIT, d.h. electron-beamion-trap eingesetzt werden. Interessanterweise kann man hier wieder das Prinzip umgehen, daß man im freien Raum kein Maximum des elektrischen Feldes produzieren kann. Der Elektronenstrahl stellt zwar im Prinzip Materie dar, ähnlich einem aufgeladenen Draht in der Fallenmitte, ist aber für die schweren Ionen durchdringbar. Nachdem die Ionen dann auf den geeigneten Ladungsbereich gebrütet wurden, werden sie dann extrahiert. Dieser Quellentyp arbeit also gepulst. 99 Abbildung 116: EBIS Quelle. Quelle: CRYEBIS-Gruppe, Kansas-State- University. 100 6.2 Ionenfallen Problem: in statischen elektrischen Feldern enden die Feldlinien auf den geladenen Oberflächen. Man kann keine statischen, stabilen Gleichgewichtspunkte im Vakuum finden. Trotzdem kann man Ionenfallen mit statischen Feldern konstruieren. 6.2.1 Kingdonfalle (1923) Sie besteht einfach aus einem geladenen Draht in der Mitte, der die Ionen anzieht (radialer Einschluß), und zwei abstoßenden Endkappen (axialer Einschluß). Die Erhaltung des Drehimpulses verhindert, daß die Ionen auf den Draht stürzen. Allerdings modifizieren Stöße mit dem Hintergrundgas den Drehimpuls, sodaß die Lebensdauer in dieser Falle recht kurz ist (etwa 1 sec bei 10−8 mbar). Bemerkenswert ist, daß alle zirkularen Orbits die gleiche kinetische Energie aufweisen, alle Orbits haben die gleiche mittlere kinetische Energie. Dieser Fallentyp wird relativ selten benutzt. Eine weitere statische Falle ist die Penningfalle, die später ausführlich diskutiert wird. Wie schon erwähnt, ist auch die EBIT eine statische Falle, die das Problem mit dem zentralen Draht umgeht. 6.2.2 RF-Ionenfalle oder Paulfalle Hier werden dynamische (zeitabhängige) Felder zum Einschluß der Ionen verwendet, und zwar in der Regel Quadrupolfelder. Das Quadrupolfeld weist ein Potential der Form φ = φ0 2 2 2 λx + σy + γz 2r02 auf, wobei φ0 dem extern angelegten Potential entspricht und r0 von der Geometrie abhängt. Außerhalb der Elektroden erfordert die Laplacegleichung λ + σ + γ = 0. Zweidimensionaler Fall Historisch war zunächst der zweidimensionale Quadrupol von Bedeutung, z.B. γ = 0, λ = −σ = 1, mit dem Potential φ(x, y) = φ0 x2 − y 2 . 2r02 Ein derartiges Feld wird experimentell mit einer Struktur wie in Abb. 117 erzeugt. Jetzt sollen an diese Struktur zeitabhängige Spannungen angelegt werden: φ(x, y, t) = (U − V cos (Ωt)) x2 − y 2 . 2r02 Für ein geladenes Teilchen erhält man dann die Bewegungsgleichungen e (U − V cos (Ωt)) x = 0 mr02 e ÿ − (U − V cos (Ωt)) y = 0 mr02 z̈ = 0. ẍ + 101 Abbildung 117: Elektrodenstruktur für den zweidimensionalen Quadrupol. Quelle: Ghosh. Mit den Substitutionen 4eU mr02 Ω2 2eV q = mr02 Ω2 Ωt = 2ζ a = erhält man die Gleichungen d2 x + (a − 2q cos (2ζ))x = 0 dζ 2 d2 y − (a − 2q cos (2ζ))y = 0. dζ 2 Hierbei handelt es sich um Differentialgleichungen des Mathieuschen Typs. Ohne auf die Lösung dieser Gleichungen näher einzugehen, beschränken wir uns hier auf das wesentliche Merkmal: es gibt nur für bestimmte Werte von a und q stabile Lösungen. Das Diagram 118 zeigt dies. Betreibt man den Quadrupol mit Parametern a, q, so daß x und y stabil sind, erhält man in der x-y Ebene gebundene Trajektorien. Anschauliche Beschreibung und Prinzip der starken Fokussierung Ein statischer Quadrupol kann Teilchen natürlich nicht auf einer stabilen Bahn halten. In einer Dimension werden die Teilchen in die Mitte des Quadrupols gedrückt, gleichzeitig ziehen die beiden anderen, senkrecht dazu stehenden Elektroden die Ionen an, diese werden also in einer Richtung zusammengedrückt und senkrecht dazu aus der Anordnung herausgequetscht. Polt man nun die Elektroden zeitlich in geeigneter Weise um, kann man die Teilchen jedoch wieder in die Mitte zurückdrücken, wobei sie dann aber senkrecht dazu wieder anfangen herauszulaufen usw. Der wesentliche Punkt ist nun, daß man bei geeigneter Wahl der RF in beiden Dimension netto eine Kraft in die Quadrupolmitte erhält. Dies resultiert von der Tatsache, daß die nach außen wirkende (defokussierende) Kraft immer angreift, wenn 102 Abbildung 118: Stabilitätsdiagramm der Mathieuschen Differentialgleichung. Quelle: Ghosh. die Teilchen in der Mitte sind, die nach innen drückende (fokussierende) Kraft aber auf die Teilchen wirkt, die schon nach außen gewandert sind. Aus der Form des Quadrupolfeldes erkennt man aber, daß das Feld in der Mitte sehr klein ist und nach außen hin linear ansteigt. Das heißt daß im Mittel die fokussierende Kraft stärker ist als die defokussierende. Dieser Effekt ist die sog. starke Fokussierung, wie sie ursprünglich für die Synchrotrons der Hochenergiephysik erfunden wurde: selbst ein perfekt kollimierter Teilchenstrahl bläht sich, z.B. durch die eigene Raumladung, schnell auf und nach wenigen Umläufen im Synchrotron wäre der Strahl verloren. Deshalb muß man natürlich fokussierende Elemente in den Ring einbauen. Das magnetische Äquivalent zur optischen Linse ist der statische Quadrupolmagnet. Auch der Quadrupolmagnet hat das Problem, daß er nur in einer Richtung fokussiert, in der anderen jedoch defokussiert. Nimmt man jetzt wieder zwei Quadrupolmagnete hintereinander, mit um 90 Grad versetzten Polschuhen, dann hat man auch wieder den Effekt daß für beide transversalen Richtungen Fokussierung und Defokussierung stattfindet, der Nettoeffekt jedoch in beiden Dimensionen einer Fokussierung entspricht. In der Optik kann man den gleichen Effekt beobachten: schaltet man zwei Linsen, eine konvexe (fF > 0) und eine konkave (fD < 0) mit einem Abstand l hintereinander, hat diese Anordnung bei geeignetem l eine fokussierende Wirkung, in der linearen Näherung (dünne Linsen) erhält man für die Gesamtbrennweite f des Linsendoubletts f = fF fD . fF + fD − l In der Speicherringphysik nennt man solch eine Struktur ein FODO-Zelle, F für den fokussierenden Magnet, 0 für die Driftstrecke und D für den defokussierenden Magnet. Das Paulsche Quadrupolmassenfilter Die erste Anwendung der zweidimensionalen RF-Quadrupolstruktur war das Massenfilter (W. Paul, 1952, Nobelpreis 1989). Dabei macht man sich zunutze, daß die Parameter a, q in der Mathieu-Gl. vom Masse-zu- Ladungsverhältnis m/Q der Teilchen abhängen. Hält man z.B. das Verhältnis U/V = a/q konstant und fährt beide Spannungen hoch, läuft man in a − q Diagramm auf einer Ursprungsgeraden (siehe Abb. 119) hoch. Nur in einem bestimmten Bereich von m/Q-Werten befindet man sich innerhalb des Stabilitätsbereichs und nur solche Teilchen können das Massenfilter ungehindert durchlaufen. Die geeignete Wahl des Verhältnisses U/V gestattet es, die Güte des Massenfilters zu beeinflussen. 103 Abbildung 119: Stabilitätsdiagramm der Mathieuschen Differentialgleichung, Vergrößerung des 1. Stabilitätsbereichs. Quelle: Ghosh. Die lineare Paulfalle Man kann den zweidimensionalen Quadrupol auch als Falle verwenden. Anstatt einen Strahl durchzuschiessen, versieht man die beiden Enden mit abstoßenden Endkappen. Diese Art von Falle wurde bei Laserkühlexperimenten (auch Quantencomputern) populär, da das Potentialminimum einer ganzen Linie entspricht, und nicht wie bei der 3D-Falle (siehe unten) nur ein einziger Punkt ist. Dadurch kann man mehr Ionen in die Falle laden und Effekte wie RF-Heizung werden minimiert. Die dreidimensionale Paulfalle Hierzu verwendet man ein “echtes” dreidimensionales Quadrupolfeld, z.B. λ = σ = 1, γ = −2. Die Idealform der Elektroden sind hyperbolische Flächen, wie in Abbn. 120 und 121 gezeigt. Abbildung 120: Hyperbolische Paulfalle. Quelle: W. Paul, Review of Modern Physics, Vol. 62 (1990). 104 Abbildung 121: Hyperbolische Paulfalle. Quelle: W. Paul, Review of Modern Physics, Vol. 62 (1990). In diesem Falle haben wir Rotationssymmetrie in der x-y Ebene, die Feldstärke hängt also nur vom radialen Abstand r um die z-Achse und von z ab. Man erhält dann Stabilitätsdiagramme für r und z. Durch die unterschiedlichen Gradienten sind die Definitionen von a und q achsenspezifisch: az qz ar qr = = = = a2D q2D az /2 qz /2 Das Gesamtdiagramm ist deshalb nicht mehr symmetrisch (Abb. 122). Die Bewegung des Ions in der Falle hat zwei Komponenten: (i) eine niedrigfrequente Säkulärbewegung im Pseudofallenpotential, d.h. dem zeitlich gemittelten, fokussierenden Potential, und (ii) eine schnelle Mikrobewegung mit kleinerer Amplitude aufgrund der direkten Antwort des Teilchens auf die angelegte Hochfrequenz. Übrigens kann man auch makroskopische Metallpartikel in Paulfallen fangen und mithilfe von gestreutem Licht die Trajektorien sichtbar machen (Wuerker et al. 1959, Abb. 123). Ein mechanisches Analogon für die RF-Falle ist in Abb. 124 gezeigt. Eine auf den Sattel gelegt Kugel rollt sofort hinunter, läßt man aber den Sattel mit der geeigneten Frequenz rotieren, kann die Kugel auf dem Sattel stabilisiert werden. Anmerkungen: • Die bisher gezeigten Stabilitätsdiagramme gelten für ein einzelnes Teilchen in der Falle. Größere Mengen von gefangen Ionen sorgen durch Raumladungseffekte für Verschiebungen im Diagramm. 105 Abbildung 122: Stabilität in der 3-dim. Paulfalle. Quelle: Ghosh. • Falls die genaue Form des Potentials keine Rolle spielt, kann man auf hyperbolische Elektroden verzichten und z.B. eine Paulfalle ganz aus gebogenen Drähten herstellen. Ebenso ist es möglich, sehr kleine Fallen lithographisch, quasi auf einem “Chip”, herzustellen, was in den Abbildungen 125 und 126 illustriert ist. 6.2.3 Penningfalle Die Penningfalle ist eine rein statische Falle mit elektrischen und magnetischen Feldern. Die Elektrodenkonfiguration ist ähnlich der der Paulfalle und ist in Abb. 127 gezeigt. Auch in diesem Fall erhält man ideale Potentiale mit hyperbolischen Oberflächen, die die Gleichung r2 z 2 − = ±1 r02 z02 erfüllen. Die beiden Endkappen sorgen in z-Richtung für Abstoßung, was zu einer harmonischen Oszillation mit der axialen Frequenz ω0z = s 4eU m(2z02 + r02 ) führt. In der x-y Ebene drängt das elektrische Feld die Teilchen nach außen, aber das homogenen magnetische Feld in z-Richtung verhindert das Erreichen der Elektroden. Es entsteht eine Zyklotronbewegung um die magnetischen Feldlinien mit ωc = eB/m. Dies führt jedoch zu einer sogenannten E × B-Drift im gemischten magnetischen und elektrischen Feld (Details sind z.B. in Jackson zu finden). Bezüglich der Lösung dieses Problems sei z.B. auf Ghosh [15] verwiesen, das Resultat sieht folgendermaßen aus: in der x-y Ebene erhält man zwei kreisförmige Bewegungen: 106 Abbildung 123: Makroskopische Teilchen in der Paulfalle. Quelle:W. Paul, Review of Modern Physics, Vol. 62 (1990). • eine modifizierte Zyklotronbewegung um die magnetischen Feldlinien mit der Frequenz ω0+ = q 2 2 (ωc + ωc − 2ω0z )/2. q 2 • eine Magnetronbewegung um das Fallenzentrum mit der Frequenz ω0− = (ωc − ωc2 − 2ω0z )/2. Beispiel für Orbitale in der Penningfalle sind im Bild 128 gezeigt. Typische Parameter einer Penningfalle: • r0 = 0.8 cm • U =8V • B =6T • νc = 901 kHz • ν0z = 78 kHz 107 Abbildung 124: Mechanisches Modell der Paulfalle. Quelle:W. Paul, Review of Modern Physics, Vol. 62 (1990). Abbildung 125: Prinzip der lithographischen, linearen Paulfalle. Quelle: Mary Rowe, NIST, Boulder. • ν0+ = 898 kHz • ν0− = 3.4 kHz Bemerkenswert ist daß die Magnetronbewegung eigentlich instabil ist. Ihr Energiebeitrag ist negativ. Wenn das Ion auf eine größere Magnetronbahn kommt, senkt sich die Gesamtenergie ab. Das Wandern nach außen geschieht jedoch sehr langsam, deshalb ist die Magnetronbewegung metastabil. Ein Problem sind jedoch Teilchenkollisionen. 108 Abbildung 126: Photo der lithographischen, linearen Paulfalle. Quelle: Mary Rowe, NIST, Boulder. Abbildung 127: Querschnitt durch eine Penningfalle. Quelle: Ghosh. 6.2.4 Kühlung in Ionenfallen Puffergaskühlung Ionenfallen haben im Vergleich zu Neutralfallen sehr tiefe Potentiale, d.h. Hintergrundgasstöße müssen nicht fatal sein und können daher zum Kühlen herangezogen werden, wenn das Puffergas kälter als die Fallenionen ist (z.B. kaltes Helium). Probleme mit dieser Methode kann es bei Penning- und Kingdonfallen geben. Die Mikroteilchenfalle von Wuerker et al. operierte z.B. mit 0.01 Torr Puffergas. 109 Abbildung 128: Bewegung eines Ions in der Penningfalle. Quelle: Ghosh. Widerstandskühlung Die Ionenfalle wird hier Teil eines externen elektrischen Schwingkreises, der in Resonanz, z.B. mit der axialen Ionenbewegung, gebracht wird. Über die ohmschen Verluste des externen Schwingkreises wird dann der Ionenschwingung Energie entzogen. Allerdings muß hierzu der externe Schwingkreis extrem kalt sein, damit das Temperaturrauschen nicht auf die Ionen übertragen wird (siehe Abb. 129). Die Kühlrate ist recht gering, man benötigt einige Sekunden. Übrigens ist ein solcher Schwingkreis auch ein wichtiges Mittel, um die Ionen in der Falle überhaupt zu detektieren. Stochastisches Kühlen Die vom oszillierenden Ion erzeugte Spiegelladung auf einer Elektrode wird detektiert. Mithilfe schneller Elektronik wird dann auf die Gegenelektrode ein Signal geeigneter Phasenlage gegeben, das die Schwingung abbremst. Im Vergleich zur Widerstandskühlung kann dies schneller geschehen. Diese Methode stammt aus der Beschleunigerphysik. In den großen Protonenspeicherringen (CERN SPPS, Fermilab Tevatron) ist sie der Hauptkühlmechanismus. Synchrotrons für Elektronen haben übrigens einen automatischen Kühlmechanismus eingebaut: die Kreisbewegung der hochenergetischen Elektronen verursacht Synchrotronsstrahlung, die schnellen Elektronen im Ensemble strahlen dabei mehr ab als die langsamen und der Strahl kühlt sich ab, wird allerdings auch immer langsamer, deshalb muß ständig nachbeschleunigt werden. Laserkühlung Genau wie bei neutralen Atomen kann man mit einem rotverstimmten Laser auch Ionen in einer Falle kinetische Energie entziehen (Dehmelt und Wineland, 1975). Für das in der Falle oszillierende Ion gibt es zwei Regimes: 110 Abbildung 129: Widerstandskühlung. Quelle: Ghosh. (i) Schwere Teilchen (ν Γ, wobei ν die Oszillationsfrequenz des Ions in der Falle ist und Γ die Linienbreite des atomaren Übergangs). Falls der Laser nicht zu sehr verstimmt ist, gibt es dann auf der Trajektorie des Ions zwei lokalisierte Punkte wo der Laser in Resonanz mit dem Ion kommt, wie in Abb. 130 gezeigt. (ii) Schnelle Teilchen (ν Γ). Die spontane Emission findet entlang der gesamten Trajektorie statt. Die Ruhefrequenz des Übergangs wird durch den Dopplereffekt frequenzmoduliert. Deshalb erscheinen im Spektrum Seitenbänder. E(t) ∝ exp [−i(ωt + = exp (−iωt) kv0 sin (νt))] + c.c. ν +∞ X Jl (kv0 /ν) exp (−ilν t), l=−∞ wobei Jl eine Besselfunktion ist. Man erhält durch die Frequenzmodulation also Seitenbänder bei ω + lν, l = −∞..∞. In diesem Fall kann man Kühlung durch Anregung auf einem Seitenband und spontanem Zerfall auf dem Träger interpretieren (Abb. 131). Abbildung 130: Laserkühlung für langsame Ionen, die Dopplerbedingung ist genau an zwei Punkten der Ionentrajektorie erfüllt. Quelle: Ghosh. Laserkühlung wurde 1978 von zwei Gruppen zum ersten Mal erziehlt, in Hamburg von der Gruppe um P. Toschek und in Boulder von D. Wineland. Man kann Temperaturen von Kelvin bis hinunter zu einigen mK erreichen. Tabelle 132 gibt einen Überblick über bisher verwendete Ionenspezies. 111 Abbildung 131: Laserkühlung für schnelle Ionen. Im Bild befindet sich das Ion im ersten angeregten Schwingungszustand der Falle (die Bewegung ist jetzt quantisiert); durch Anregung in den angeregten elektronischen Zustand und anschließende spontane Emission kann man in den unteren Schwingungszustand kommen. Quelle: Ghosh. Abbildung 132: Ionensorten für Laserkühlung. Quelle: R.C. Thompson, Advances in Atomic, Molecular, and Optical Physics, Vol. 31, 63 (1993). Sympathetisches Kühlen Zwei Sorten von Ionen werden gleichzeitig geladen, eine davon ist laserkühlbar. Durch Coulombwechselwirkung wird die zweite Spezies “dunkel” mitgekühlt. Dabei kann es sich z.B. auch um zwei Isotope des gleichen Elements handeln. Mithilfe dieser Methode kann man ein Ion kühlen, ohne es direkt resonanter Strahlung auszusetzen. 112 6.2.5 Experimente in Ionenfallen g-2 Experimente In diesen Versuchen mißt man das anomale magnetische Moment des Elekrons (oder Positrons,Müons). Derzeit ist dies der genaueste Test der QED. Im Magnetfeld der Penningfalle hat man ein Larmorbewegung mit ωc = eB/m sowie eine Spinpräzession. Die Spinzustände entsprechen Energien Es = −gms µB B, d.h. zum Spinumklappen ist eine Energie ∆Es = geh̄B/2m notwendig, entsprechend einer RF-Frequenz ωs . Durch Vergleich der Zyklotronfrequenz ωc mit der Spinumklappfrequenz ωs erhält man ωs /ωc = g/2. Gemessen wird im Experiment der Frequenzunterschied ωa = ωs − ωc . Das ganze ist etwas komplizierter, da wie oben erwähnt, die Frequenzen in der Penningfalle modifiziert sind. Experimentell hat man Zugriff auf ωa0 = ωs − ωc + ω0− . Die Anomalie des g-Faktors (d.h. die Abweichung von 2) wird dann gemessen durch 2 g−2 ωa0 − (ω0z /2ω0+ ) = . 2 2 ω0+ + (ω0z /2ω0+ ) Der momentan beste Werte (Gruppe von H. Dehmelt und R. VanDyck, U.o.Washington) ist g − (e ) = 1.001 159 652 188 4(4.3), 2 eine der am genauesten gemessenen Naturkonstanten überhaupt. Die System eines einzelnen Elektrons in einer Penningfalle wurde von Dehmelt Geonium genannt. Geonium ist in gewisser Weise ein künstliches Atom, mit diskreten Anregungen entsprechend der Axial-, Zyklotron- und Magnetronbewegung. Ein Leveldiagramm ist in Abb. 133 gezeigt. Quantensprünge In Ionenfallen kann man die Fluoreszenz eines einzelnen Ions beobachten. Bei geeigneten Zuständen kann man sehen, wie das Ione Sprünge in verschiedene Level macht, so z.B. in Quecksilber. Mithilfe ultravioletter Strahlung (194 nm) kann man das Hg-Ion vom 2 S1/2 in den 2 P1/2 Zustand anregen, von wo es wieder herunterfallen kann. Allerdings zeigt Bild 134, daß auch ein Übergang in die metastabilen D-Zustände möglich ist. Passiert dies, bleibt das Ion dort für einige Zeit und die Absorption und Streuung des Lichts unterbleibt. Man beobachtet dann, wie das Ion plötzlich dunkel wird. Fällt es dann schließlich wieder in den Grundzustand, wird es wieder hell (Abb. 135). Ionenkristalle Mit Laserkühlung kann man in einen Bereich vordringen, wo die kinetische Energie der Ionen kleiner wird als die Coulombwechselwirkung zwischen ihnen, die Ionen arrangieren sich dann in einem Kristall. Interessant ist, daß dann Mechanismen wie die RF-Heizung, die die Ionen in der Paulfalle aufheizen, ausgeschaltet werden, da es zu keinen Stößen mehr kommt. An diesen Kristallen kann man, ähnlich wie bei Clustern, Schalenstrukturen beobachten, Phasenübergänge, Störstellen, Fremdionen etc. Im Kontext der derzeit heißdiskutierten Quantencomputer sind Kristalle in linearen Paulfallen ins Zentrum des Interesses gerückt, seit in einem solchen Aufbau von der Wineland-Gruppe in Boulder die ersten Quantenbitmanipulationen durchgeführt wurden. Die Bilder 136, 137, 138 und 139 zeigen verschiedene Kristalle. Die Masse des Antiprotons Mithilfe der Zyklotronfrequenz in einer Penningfalle kann man natürlich auch die Masse des gespeicherten Ions messen, sofern das Magnetfeld genau genug bekannt ist. Am Antiprotonenspeicherring LEAR am CERN ist es der Gruppe um G. Gabrielse (Harvard) gelungen, Antiprotonen (die in Kollisionen bei mehr als 4 GeV erzeugt werden müssen) abzubremsen und in eine Penningfalle zu laden. Dort wurde dann durch die Zyklotronfrequenz die Masse der Antiprotons 113 Abbildung 133: Geonium. Quelle: Ghosh. Abbildung 134: Leveldiagramm für 199 Hg. Die D Zustände sind metastabil. Quelle: W. Itano et al, Phys. Rev. Lett. 59, 2732-2735 (1987). mit der des Protons verglichen (Bild 140). Im bisher letzten und genauesten Experiment (Gabrielse et al.,Physical Review Letters 82, 3198 (1999)) wurde statt des Protons H− verwendet und als Resultat kam heraus daß die Ladungs- zu-Masse Verhältnisse für das Antiproton und das Proton auf 114 Abbildung 135: Quantensprünge in (1987). 199 Hg. Quelle: W. Itano et al, Phys. Rev. Lett. 59, 2732-2735 Abbildung 136: Ionenkristall aus Kalziumionen. Quelle: Webseite der Werth-Gruppe an der Univ. Mainz. Abbildung 137: Lineare Kette in einer linearen Paulfalle. besser als 10−10 übereinstimmen. Dies ist der genaueste Test des CPT-Theorems, welches besagt daß alle physikalische Prozesse unter einer simultanen Paritäts-, Ladungskonjugations- und Zeitumkehrtransformation invariant sind. Das CPT-Theorem kann aus sehr grundlegenden Annahmen über Feldtheorien hergeleitet werden. 115 Abbildung 138: Aufbau einer Schalenstruktur im Ionenkristall. Abbildung 139: Einbau eines Fremdions in einen Kristall. 116 Abbildung 140: Vergleich der Masse des Antiprotons mit der seines Antiteilchens, des Protons. Quelle: Ghosh. 117 Literatur [1] G. Scoles, Atomic and Molecular Beam Methods, Vol. 1, Oxford Univ. Press. [2] Bergmann-Schaefer, Lehrbuch der Experimentalphysik, Bd. 4. De Gruyter, Berlin. [3] H. Haken und H.C. Wolf, Atom- und Quantenphysik, Springer Verlag. [4] D.A. Bromley, Treatise in Heavy-Ion Science, Bd. 8, Plenum Press, New York. [5] J.H. Moore, C.C. Davis, M.A. Coplan, Building Scientific Apparatus, Addison-Wesley,1989. [6] W.R. Leo, Techniques for Nuclear and Particle Physics Experiments, Springer, 1987. [7] W. Demtröder, Laserspektroskopie 4. Auflage. Springer Heidelberg, 2000. [8] B.H. Bransden und C.J. Joachain, Physics of Atoms and Molecules, Longman, 1983. [9] A.E. Siegman, Lasers, University Science Books, 1986. [10] B. Saleh und M.C. Teich, Fundamentals of Photonics, Wiley 1991. [11] N. Ramsey, Molecular Beams, Oxford 1956. [12] L. Allen und J.H. Eberly, Optical Resonance and Two-Level Atoms, Dover Publications 1975. [13] J.J. Sakurai, Modern Quantum Mechanics, Addison-Wesley 1985. [14] E. Arimondo, W.D. Phillips und F. Strumia, Manipolazione col laser di atomi e ioni, CXVIII corso, Amsterdam 1991. Scuola internazionale di fisica “Enrico Fermi”, North Holland. [15] P.K. Ghosh, Ion Traps, Oxford Clarendon Press, 1995. 118






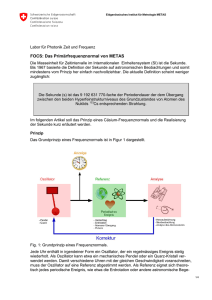
![2. Tag: Atommodelle [1, 2] 1. Atomtheorie 2. Der Aufbau der Atome](http://s1.studylibde.com/store/data/002489402_1-195f0685b92c2c6d270c65292bba19f4-300x300.png)