1. Elementare Dreiecksgeometrie - TU Wien

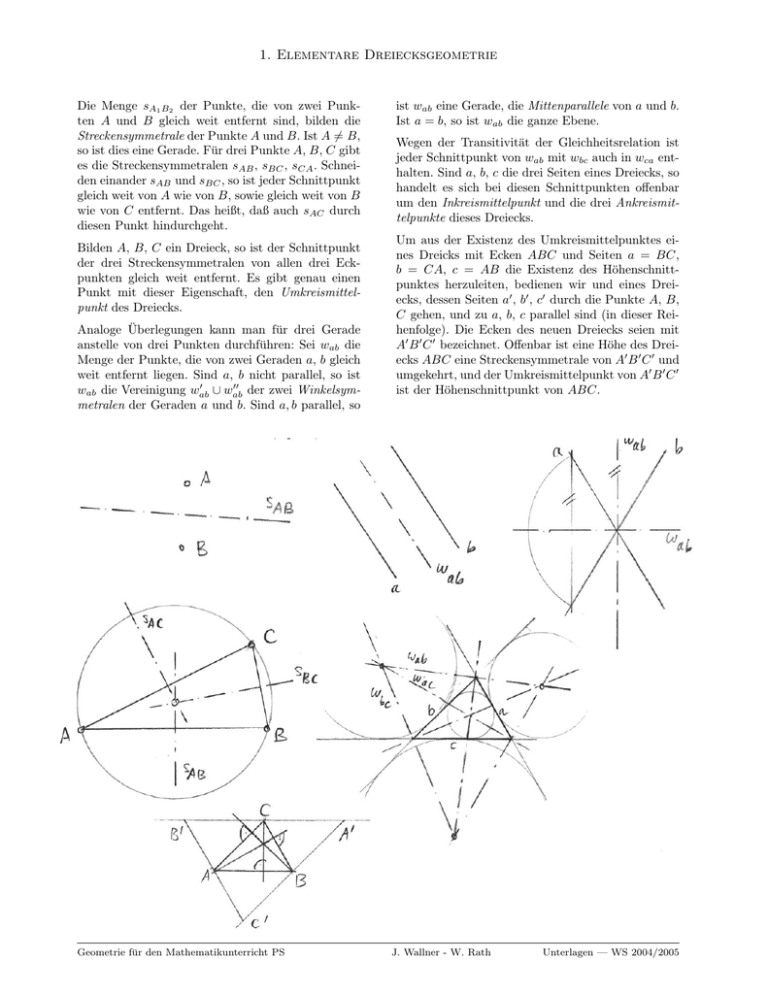
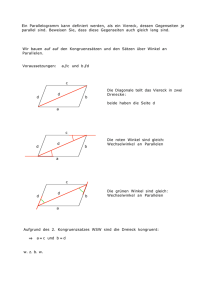
1. Elementare Dreiecksgeometrie
Die Menge sA1 B2 der Punkte, die von zwei Punkten A und B gleich weit entfernt sind, bilden die
Streckensymmetrale der Punkte A und B. Ist A 6= B,
so ist dies eine Gerade. Für drei Punkte A, B, C gibt
es die Streckensymmetralen sAB , sBC , sCA . Schneiden einander sAB und sBC , so ist jeder Schnittpunkt
gleich weit von A wie von B, sowie gleich weit von B
wie von C entfernt. Das heißt, daß auch sAC durch
diesen Punkt hindurchgeht.
Bilden A, B, C ein Dreieck, so ist der Schnittpunkt
der drei Streckensymmetralen von allen drei Eckpunkten gleich weit entfernt. Es gibt genau einen
Punkt mit dieser Eigenschaft, den Umkreismittelpunkt des Dreiecks.
Analoge Überlegungen kann man für drei Gerade
anstelle von drei Punkten durchführen: Sei wab die
Menge der Punkte, die von zwei Geraden a, b gleich
weit entfernt liegen. Sind a, b nicht parallel, so ist
0
00
wab die Vereinigung wab
∪ wab
der zwei Winkelsymmetralen der Geraden a und b. Sind a, b parallel, so
Geometrie für den Mathematikunterricht PS
ist wab eine Gerade, die Mittenparallele von a und b.
Ist a = b, so ist wab die ganze Ebene.
Wegen der Transitivität der Gleichheitsrelation ist
jeder Schnittpunkt von wab mit wbc auch in wca enthalten. Sind a, b, c die drei Seiten eines Dreiecks, so
handelt es sich bei diesen Schnittpunkten offenbar
um den Inkreismittelpunkt und die drei Ankreismittelpunkte dieses Dreiecks.
Um aus der Existenz des Umkreismittelpunktes eines Dreicks mit Ecken ABC und Seiten a = BC,
b = CA, c = AB die Existenz des Höhenschnittpunktes herzuleiten, bedienen wir und eines Dreiecks, dessen Seiten a0 , b0 , c0 durch die Punkte A, B,
C gehen, und zu a, b, c parallel sind (in dieser Reihenfolge). Die Ecken des neuen Dreiecks seien mit
A0 B 0 C 0 bezeichnet. Offenbar ist eine Höhe des Dreiecks ABC eine Streckensymmetrale von A0 B 0 C 0 und
umgekehrt, und der Umkreismittelpunkt von A0 B 0 C 0
ist der Höhenschnittpunkt von ABC.
J. Wallner - W. Rath
Unterlagen — WS 2004/2005
2. Der Satz des Pythagoras
Dieser Satz, der in der Form “a2 + b2 = c2 ”
sprichwörtlich geworden ist, trägt den Namen des
Pythagoras von Samos (ca. 580–ca. 500 v.Chr.), ist
aber sicher nicht von ihm entdeckt worden. In einer
geometrischen Sprache können wir ihn so formulieren:
Satz 1. (des Pythagoras) In einem rechtwinkeligen
Dreieck ist die Summe der Flächeninhalte der Quadrate über den Katheten gleich dem Flächeninhalt
des Quadrates über der Hypotenuse.
Es gibt sehr viele verschiedene Beweise dafür — der
Kuriosität halber sei erwähnt, daß der Beweis von
James Garfield (1831–1881) der einzige dem Autor
bekannte Beitrag eines Präsidenten der USA zur Mathematik darstellt.
Geometrie für den Mathematikunterricht PS
In einem geometrischen Kontext zeigen wir die
Flächengleichheit auf zwei verschiedene Arten: (i)
dadurch, daß sich die zwei Quadrate über den Katheten in endlich viele Teile zerlegen lassen, die
man zu dem Quadrat über der Hypotenuse zusammensetzen kann (die Zerlegungsgleichheit der beiden Flächen) und (ii) dadurch, daß man zu beiden Flächen (nachdem man sie passend kongruent
verlagert hat) jeweils endlich viele kongruente Teile
hinzufügen kann, sodaß das Resultat zwei euklidisch
kongruente Flächen sind (die Ergänzungsgleichheit)
der beiden Flächen.
Eine Zerlegung in fünf Teile und eine Ergänzung
durch vier kongruente Dreiecke sind aus den beiden
untenstehenden Figuren ersichtlich.
J. Wallner - W. Rath
Unterlagen — WS 2004/2005
3. Winkelbegriffe in der euklidischen Geometrie
Das Messen von Winkeln wird hier aufbauend auf
dem Begriff der Bogenlänge am Einheitskreis eingeführt. Auf dessen Präzisierung sei auf die Vorlesungen aus Analysis verwiesen. Hier wird er nur in
naiver Weise verwendet.
Verwendet man die
(−π/2, π/2], so ist
3.1 Der orientierte Winkel von Halbgeraden
und Geraden
Nicht orientierte Winkel ^( g , h) oder ^(g, h) zwischen Halbgeraden oder Geraden sind von der Reihenfolge der beiden Argumente unabhängig. Verwendet man nichtnegative Winkelmaße, so ist
Wir können Kreisen in der euklidischen Ebene eine Durchlaufsinn zuordnen — positiv oder negativ
(gegen den oder mit dem Uhrzeigersinn). Gehen von
−
→
− →
einem Punkt zwei Halbgeraden g , h aus, so ist der
orientierte Winkel
(3)
−
→
− →
− →
Intervalle
−
→
− →
− →
→
−
(−π, π]
bzw.
→
−
^( g , h) = −^( g , h), ^(g, h) = −^(g, h).
3.2 Nicht orientierte Winkel
−
→
− →
(4)
→
−
→
−
^(g, h) = min(^(g, h), ^(h, g)).
Ansonsten ist
(5)
→
−
^(g, h) = |^(g, h)|.
−
→
− →
− →
(1)
^( g , h)
definiert als die Bogenlänge desjenigen Kreisbogens,
→
−
→
−
der von g überstrichen wird, wenn wir g im ma→
−
thematisch positiven Sinn nach h drehen. Auch der
Drehung wird diese Bogenlänge als Winkel zugeordnet. Orientierte Winkel nehmen damit Werte aus
dem Intervall [0, 2π) an. Alternativ kann man auch
Winkel mit Werten in (−π, π] betrachten: In diesem Fall dreht man entweder positiv oder negativ,
je nachdem, wo die Drehung kürzer ist. Der Winkel
bekommt das entsprechende Vorzeichen.
Der orientierte Winkel von Geraden g, h ist entsprechend der Winkel der Drehung von g nach h definiert. Solche Winkel sind aus den Intervallen [0, π)
oder (−π/2, π/2].
Bei orientierten Winkeln ist die Reihenfolge der Argumente wichtig. Verwendet man nichtnegative Winkelmaße, so ist
−
→
− →
− →
− →
→
− →
−
→
−
→
−
(2) ^( g , h) = 2π − ^( h, g ), ^(g, h) = π − ^(h, g).
Geometrie für den Mathematikunterricht PS
Beide, die orientierten und nicht orientierten Winkel bleiben bei orientierungserhaltenden euklidischen
Kongruenztransformationen erhalten, d.h. bei Schiebungen und Drehungen. Die nicht orientierten Winkel bleiben auch bei orientierungsumkehrenden Kongruenztransformationen (z.B. Spiegelungen) erhalten, die orientierten Winkel ändern ihr Vorzeichen
(soferne man Werte in den Intervallen (−π, π] und
(−π/2, π/2] benützt).
3.3 Die Winkel bzw. Drehungen um einen
Punkt als Gruppe
Die Drehungen um einen festen Punkt bilden eine
Gruppe mit der Hintereinanderausführung der Drehung als Gruppenoperation.
Nachdem eine Drehung durch ihren orientierten
Winkel eindeutig festgelegt ist und umgekehrt, bilden auch die orientierten Winkel bzw. die Menge
[0, 2π) eine Gruppe. Die Gruppenoperation ist die
Addition von Winkeln modulo 2π.
J. Wallner - W. Rath
Unterlagen — WS 2004/2005
4. Winkel im Kreis
Wir betrachten einen Kreis k mit Mitte M und drei
verschiedene Punkte A, B, P ∈ k. Wir wollen annehmen, daß M und P auf derselben Seite der Geraden AB liegen. Die Dreiecke AM P und BM P
sind gleichschenkelig, und deshalb gelten die Winkelgleichheiten
(1) α = ^MAP = ^MPA,
β = ^MBP = ^MPB .
Wegen der Winkelsumme im Dreieck ist
(2)
^AMP = π − 2α,
^BMP = π − 2β.
Aus
(3)
^APB = α + β,
Satz 2. (Satz vom Sehnen-Tangenten-Winkel): Der
orientierte Winkel zwischen der Kreistangente tA in
A und der Geraden AB ist gleich
→
−
^(tA , AB) = ω/2.
^AMB = 2α + 2β
1
^AMB
2
Insbesondere ist der Winkel ^APB unabhängig von
der Lage des Punktes P . Eine ähnliche Argumentation zeigt für den Fall, daß M und P auf verschiedenen
Seiten der Geraden AB liegen, daß
1
(5)
π − ^APB = ^AMB
2
gilt. Betrachtet man nicht Winkel der Form AP B,
sondern Winkel zwischen Geraden, so erhält man:
^APB =
Satz 1. (Peripheriewinkelsatz) Wir nehmen an, daß
A, B auf einem Kreis mit Mittelpunkt M liegen. Sei
ω der orientierte Winkel den die Strahlen M A und
M B einschließen (−π ≤ ω ≤ π). Dann ist der orientierte Winkel (∈ [−π/2, π/2]) zwischen den Geraden
AP und BP gleich ω/2.
In dem speziellen Fall, daß B gleich dem A gegenüberliegenden Punkt A0 am Kreis ist (d.h.
^AMB = ω = π), erhält man den Satz von Thales:
(6)
Für die bisher ausgeschlossenen Fälle A = P
und B = P könnten wir einen Grenzübergang
durchführen und die Geraden AP bzw. BP durch
die Kreistangenten in A bzw. B ersetzen. Daß dies
tatsächlich möglich ist, besagt
(7)
folgt
(4)
Dieses sieht man auch dadurch ein, daß man AP A0
durch Spiegelung an AA0 zu einem Rechteck ergänzt.
^APA0 = π/2.
Geometrie für den Mathematikunterricht PS
Beweis. Dies folgt sofort aus dem rechten Winkel
zwischen tA und AM , sowie aus der Winkelsumme
im Dreieck AM B.
Es gilt ferner die folgende Umkehrung des Peripheriwinkelsatzes:
Satz 3. Es seien Punkte A, B auf einem Kreis
mit Mittelpunkt M gegeben, und sei ω der orientierte Winkel zwischen den Strahlen M A und M B
(−π ≤ ω ≤ π). Schließen zwei Gerade g durch A
und h durch B den orientierten Winkel ω/2 ein, so
schneiden sie einander auf dem Kreis.
Beweis. Sei P der Restschnittpunkt der Geraden g
mit dem Kreis. Im Fall P 6= A, B schließen die Geraden g = AP und BP den orientierten Winkel ω/2
ein, und BP ist gleich der Geraden h.
Im Fall P = A ist g die Kreistangente in A. Nach
dem Satz vom Sehnen-Tangentenwinkel muß h =
AB sein.
Im Fall P = B ist g = AB. Nach dem Satz vom Sehnen-Tangentenwinkel muß h die Kreistangente in B
sein.
J. Wallner - W. Rath
Unterlagen — WS 2004/2005
5. Spiegelungen in der euklidischen Ebene
Die euklidische Ebene wird durch eine Gerade in
zwei Halbebenen geteilt. Eine Gerade g wird durch
einen Punkt in zwei Halbgerade (oder Strahlen) geteilt.
→
−
Wir bezeichnen Halbgerade mit dem Symbol g . Die
→
−
Gerade, auf der g liegt, wird dann mit g bezeichnet. Die zu einer Halbebene gehörige Gerade heißt
Randgerade, und der zu einer Halbgeraden gehörige
Punkt heißt Anfangspunkt.
Wir kennzeichnen die Halbgeraden mit Anfangspunkt O durch den orientierten Winkel (modulo 2π)
→
−
zu einer festen Halbgeraden x (‘x-Achse’ mit Winkel 0). Gerade durch O sind ebenfalls durch ihre
orientierten Winkel (modulo π) zur x-Achse festgelegt. Wir indizieren Gerade und Halbgerade mit dem
→
−
Winkel, den sie mit x bzw. x einschließen:
(1)
→
− →
− →
−
^( x, g α ) = α,
→
−
^(x, gβ ) = β.
5.1 Drehungen um einen festen Punkt
Lemma 1. Eine Drehung ρ mit Zentrum O und orientiertem Winkel γ bzw. eine Spiegelung σ an gα
transformiert Halbgerade durch O wie folgt:
(2)
→
−
→
−
→
−
→
−
→
−
→
−
ρ : g φ 7→ g φ+γ , σ : g α−ψ 7→ g α+ψ , g φ 7→ g 2α−φ .
Satz 1. Die Zusammensetzung von zwei Spiegelungen σα , σβ mit Achsen gα , gβ ist eine Drehung mit
dem Winkel 2(β − α).
Beweis. Die Abstände von Punkten von O bleiben
bei Spiegelungen erhalten. Es genügt daher, die Bil→
−
der von Halbgeraden g φ zu untersuchen:
(3)
→
−
→
−
→
−
σβ σα ( g φ ) = σβ ( g 2α−φ ) = g 2β−2α+φ
Geometrie für den Mathematikunterricht PS
5.2 Schiebungen orthogonal zu einer festen
Richtung
Etwas Ähnliches können wir für eine Parallelschar
von Geraden durchführen. Wir messen den orientierten Abstand einer Geraden der Schar zu einer festen
Geraden g0 durch den orientierten Abstand von g0
(d.h. der Abstand ist positiv, wenn die Gerade in einer vorher ausgezeichneten Halbebene mit Rand g0
liegt). Schiebungen orthogonal zu g0 sind durch ihre
orientierte Schiebstrecke gekennzeichnet.
Lemma 2. Eine Schiebung τ orthogonal zu g0 mit
Schiebstrecke c (c ∈ R) bzw. eine Spiegelung σ an
der Geraden ga bildet Gerade gx in der Form
(4)
τa : gx 7→ gx+c , σ : ga−y 7→ ga+y , gx 7→ g2a−x .
Satz 2. Die Zusammensetzung von zwei Spiegelungen σa , σb an ga , gb ist die Schiebung mit Schiebstrecke 2(b − a).
Beweis. Fixieren wir eine Gerade orthogonal zu g0 ,
so bleiben orientierte Abstände zu ihr bei Schiebungen und Spiegelungen erhalten. Es genügt daher, die
Bilder von Geraden gx zu betrachten:
(5)
σb σa (gx ) = σb (g2a−x ) = g2b−2a+x .
Offenbar gilt von Satz 1 und Satz 2 auch die folgende
Umkehrung: Da für beliebig gegebenes γ und α der
Winkel β = α + γ/2 die Eigenschaft 2(β − α) = γ
besitzt, können wir die Drehung mit Drehwinkel γ
zerlegen in die Spiegelung an gα (völlig beliebig) und
die Spiegelung an gα+γ/2 .
Dasselbe gilt für Schiebungen orthogonal zur Geraden g0 : Wir können die Schiebung τ mit Schiebstrecke c zerlegen in die Spiegelung an ga (beliebig)
und ga+c/2 .
J. Wallner - W. Rath
Unterlagen — WS 2004/2005