Netzwerk und gerichteter Graph

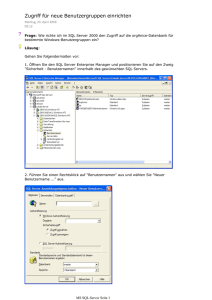
Netzwerk und gerichteter Graph
Zweig 1
3
3
Zweig 3
3
Zweig 2
R1
uq3
Zweig 4
R2
C4
L1
L5
4
2
C3
Zweig 5
1
3
1
R3
2
Elektrisches Netzwerk
1
5
2
zugehöriger gerichteter
Graph
Jedes Netzwerk besteht aus Zweigen – Kanten, die an Knotenpunkten –
Knoten miteinander verbunden sind. Im Beispiel Anzahl der Knoten m = 3
und Anzahl der Zweige n = 5. Festlegung der Bezugsrichtung im Zweig ist
willkürlich – gerichteter Graph.
Masche = geschlossener Weg aus beliebigen Zweigen. Jeder Zweig
und jeder Knoten darf nur einmal durchlaufen werden ausgenommen der
Startknoten der gleichzeitig Zielknoten ist.
VORLESUNG NETZWERKTHEORIE
GRAPHENTHEORIE – Seite 1
Baum und Baumkomplement
3
3
3
1
4
2
1
3
5
4
2
1
gerichteter Graph
5
Baum
3
1
2
2
2
1
Baumkomplement
(vollständiger) Baum – Gerüst = zusammenhängender maschenfreier
Untergraph – Gerüst, der alle Knoten des Graphen enthält. Die Zweige
eines Baumes heißen Äste, nicht zum Baum gehörende Zweige heißen
Sehnen.
Baumkomplement = Untergraph, der alle Sehnen und die zugehörigen
Knoten enthält.
VORLESUNG NETZWERKTHEORIE
GRAPHENTHEORIE – Seite 2
elektrisches Netzwerk und Schnitte
Zweig 1
3
3
3
Zweig 3
Zweig 2
R1
Zweig 4
R2
C4
1
L5
5
2
C3
Zweig 5
1
4
2
R3
L1
3
1
uq3
2
elektrisches Netzwerk
S2
S1
Schnitte S1 und S2
Werden alle Zweige eines Schnittes aus dem Graphen gestrichen,
so geht der Zusammenhang verloren. Trennlinie eines Schnittes =
geschlossene Linie (gestrichelt), die alle Schnittzweige schneidet und eine
der Komponenten umschließt.
VORLESUNG NETZWERKTHEORIE
GRAPHENTHEORIE – Seite 3
elektrisches Netzwerk – neue Zweignummern
Zweig 5
3
3
Zweig 3
Zweig 4
R5
3
uq3
Zweig 2
R4
C2
L5
L1
2
4
C3
Zweig 1
1
3
5
R3
2
elektrisches Netzwerk
1
1
2
Graph des Netzwerkes
Die Äste des Graphen erhalten immer die ersten Nummern d.h. 1 bis (m-1)
und die Sehnen erhalten die restlichen Nummern d.h. m bis n.
Zweig-Impedanzen
Z1 = jω L1; Z2 = 1/jω C2 = −j/ω C2; Z3 = R3 − j/ω C3;
Z5 = R5 + jω L5
Nur eine Spannungsquelle im Zweig 3 → Uq3 !
VORLESUNG NETZWERKTHEORIE
Z4 = R4;
GRAPHENTHEORIE – Seite 4