Kollineare Punkte - walser-h-m.ch

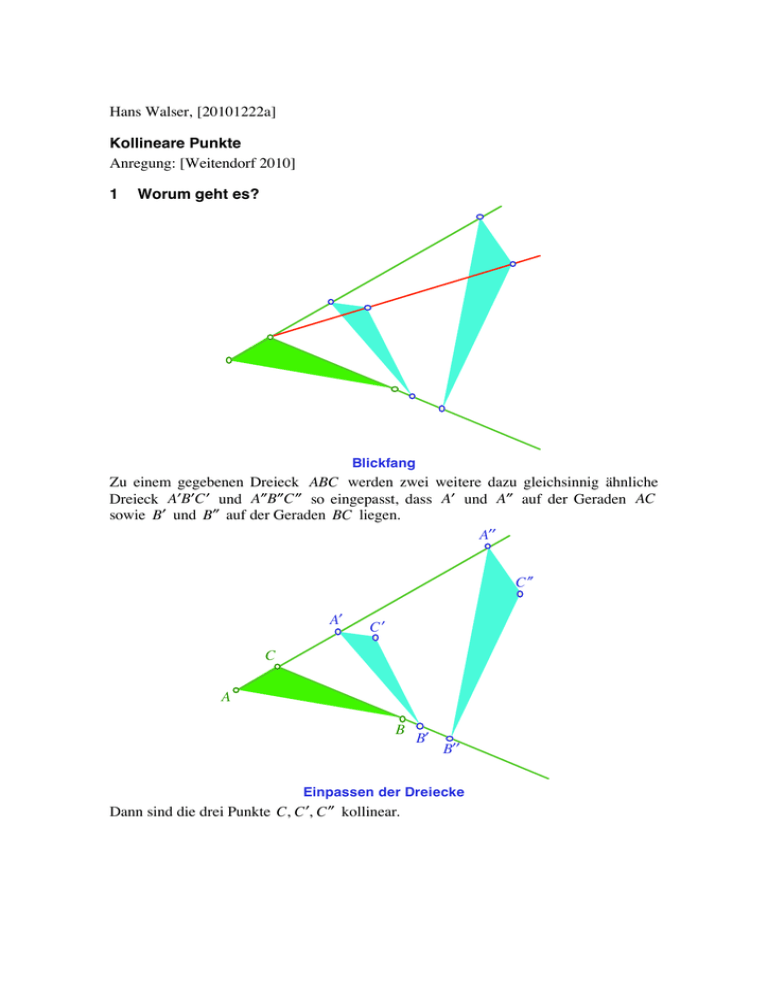
Hans Walser, [20101222a]
Kollineare Punkte
Anregung: [Weitendorf 2010]
1
Worum geht es?
Blickfang
Zu einem gegebenen Dreieck ABC werden zwei weitere dazu gleichsinnig ähnliche
Dreieck ABC und ABC so eingepasst, dass A und A auf der Geraden AC
sowie B und B auf der Geraden BC liegen.
A
C A
C
C
A
B
B
B
Einpassen der Dreiecke
Dann sind die drei Punkte C, C , C kollinear.
2/3
Hans Walser: Kollineare Punkte
2 Beweis
Das Viereck ACBC ist ein Sehnenviereck, da wir bei C und C Winkel beziehungsweise haben, die sich auf ergänzen.
A
C
C
A
B
B
Sehnenviereck
Daher ist BCC = BCC = BAC = . Analog ist BCC = . Daraus folgt die
Behauptung.
3
Variationen
Quadrat im Quadrat
3/3
Hans Walser: Kollineare Punkte
Pentagramme
Literatur
[Weitendorf 2010]
Weitendorf, Jens: Neue Technologien verändern den Mathematikunterricht! Oder: Sind Unterricht mit bzw. ohne Technologie
überhaupt noch vergleichbar? MNU Der mathematische und naturwissenschaftliche Unterricht 63/8 (1. 12. 2010), S. 452-456,
ISSN 0025-5866, © Verlag Klaus Seeberger, Neuss.