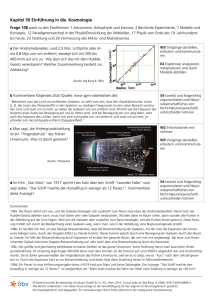
das Standardmodell der Kosmologie

10 h
h
1
5
11 h
g
un
rsc
tve
Ro
0.1
b
hie
0
0.1
2h
5
12h
0.0
1h
h
13
0.5
0
Mi
h
14
rde
n
1.0
0
23 h
llia
Lic
ht
ja
hre
1.5
0
22 h
2dF Galaxy Redshift Survey
0h
T h e m e n d e r W i ss e n s c h a f t
0
0.2
Das Standardmodell der
Kosmologie
Teil 1: Kosmologische Modelle – Ausdehnung und Alter – Entstehung der leichten
Elemente – Dunkle Materie
VON MATTHIAS BARTELMANN
Erstmals in der Geschichte der Astronomie fügen sich so gut wie
alle kosmologischen Beobachtungen in den Rahmen eines einfachen
Modells. Doch müssen wir uns damit anfreunden, dass die meiste
Materie im Universum unbekannter Natur ist und eine rätselhafte
»Dunkle Energie« das Universum beschleunigt auseinandertreibt.
U
nter den Teildisziplinen der Phy­
sik nimmt die Kosmologie eine
Sonderrolle ein. Schon die As­
trophysik kann mit ihren Gegenständen
nicht experimentieren, aber sie macht
die­se Schwierigkeit dadurch wett, dass
ihr eine große Zahl verschiedenster Him­
melskörper für Untersuchungen zur Ver­
fügung steht, etwa Sterne, Galaxien oder
noch größere Objekte. Die Kosmologie
hingegen unternimmt den Versuch, eine
physikalische Erklärung für ein einzelnes
»Objekt« zu finden, das sich ihrer Kon­
trolle entzieht: das Universum als Gan­
zes. Sie verfolgt das ehrgeizige Ziel, aus
den bekannten Naturgesetzen darauf zu
38 Sterne und Weltraum August 2007
schließen, wie das Universum sich entwi­
ckelt haben muss. Sie kann dabei zu Hilfe
nehmen, dass sich das Verhalten des Uni­
versums aus den physikalischen Eigen­
schaften zahlloser Objekte ablesen lässt,
die sie dank der endlichen Ausbreitungs­
geschwindigkeit des Lichts vor umso län­
gerer Zeit sieht, je weiter sie entfernt sind.
Welche Theorien haben wir zur Verfü­
gung, um ein Modell des Universums zu
konstruieren, das mit der beobachtbaren
Wirklichkeit verglichen werden kann?
Von den vier Grundkräften, welche die
Physik kennt, kommt nur eine zur Be­
schreibung des Universums in Frage: die
Gravitation. Die schwache und die starke
Wechselwirkung sind durch ihre endliche
Reichweite auf subatomare Skalen be­
schränkt. Die elektromagnetische Wech­
selwirkung reicht zwar wie die Gravita­
tion unendlich weit, aber da es zwei ge­
gensätzliche Ladungen gibt, kann sie sehr
wirksam abgeschirmt werden; und Mag­
netfelder, die durchaus kosmische Aus­
dehnung erreichen, sind viel zu schwach,
als dass sie einen nennenswerten Einfluss
auf das Universum ausüben könnten.
Bleibt also die Gravitation, die eine un­
endliche Reichweite hat und sich nicht
abschirmen lässt.
Symmetrie als Basis
von Weltmodellen
Nach wie vor ist Albert Einsteins Allge­
meine Relativitätstheorie die überzeu­
gendste Theorie der Gravitation, die wir
kennen. Sie hat bisher jeden noch so ri­
gorosen Test überstanden. Zwar wurde
sie nie auf kosmischen Skalen überprüft,
aber die Tatsache, dass sich ihre Konzepte
Abb. 1: Strukturen in der räumlichen Verteilung der Galaxien
sind klein gegenüber den Abmessungen des beobachtbaren
Universums. Wenn man auf geeigneten Skalen mittelt, wird die
Galaxienverteilung sehr gleichmäßig.

und Vorhersagen überall dort als richtig
erwiesen haben, wo sie experimentell un­
tersucht werden konnten, gibt uns großes
Vertrauen auch in ihre Vorhersagen zur
Kosmologie.
Die Feldgleichungen der Allgemeinen
Relativitätstheorie sind kompliziert. Um
sie zu lösen, muss man bestimmte Eigen­
schaften der Lösungen schon vorweg an­
nehmen, wie etwa ihre erwarteten Sym­
metrien. Die moderne Kosmologie be­
ginnt mit zwei Symme­trieannahmen: Die
für uns beobachtbaren Eigenschaften des
Universums mögen nicht von der Rich­
tung abhängen, in die wir beobachten,
und es gebe keine bevorzugten Beobach­
ter im Universum.
Auf den ersten Blick erscheint die
erste Symmetrieannahme geradezu ab­
surd. Sieht nicht der Nachthimmel in je­
der Richtung anders aus? Hier ist jedoch
nicht eine völlige Gleichmäßigkeit ge­
meint, sondern eine Richtungsabhängig­
keit in einem geeignet gewählten Mittel.
Die Sterne oder Galaxien, die wir hier am
Himmel sehen und dort nicht, sind sehr
klein gegenüber den Ausmaßen des ge­
samten Universums (Abb. 1). Also kann
man auf einer Längenskala mitteln, die
groß gegenüber den Galaxien, aber immer
noch klein gegenüber dem Universum ist.
Angenommen wird nur, dass das Univer­
sum nach dieser Mittelung richtungsun­
abhängig aussieht. Das mag plausibler
klingen, muss aber überprüft werden.
Den überzeugendsten Beleg dafür liefert
der kosmische Mikrowellenhintergrund,
der beinahe vollständig isotrop ist.
Die zweite Annahme erscheint weit
weniger problematisch, weil wir uns seit
Kopernikus daran gewöhnt haben, nicht
im Mittelpunkt der Welt zu stehen. Wir
halten uns jedenfalls nicht mehr für pri­
vilegierte Beobachter und erweitern diese
Erkenntnis in der erwähnten Symmetrie­
annahme auf alle anderen möglichen Be­
obachter im Universum. Wenn das Uni­
versum um uns herum isotrop ist, dann
ist es aufgrund dieser Annahme auch für
alle anderen Beobachter im Universum
isotrop. Dann muss das Universum auch
homogen sein. Damit gehen wir über das
kopernikanische Prinzip erheblich hin­
aus: Nicht nur stehen wir nicht im Mittel­
punkt der Welt, sondern ein solcher Mit­
telpunkt existiert gar nicht.
Diese beiden Symmetrieannahmen
haben nun weitreichende Konsequenzen.
Eingesetzt in Einsteins Feldgleichungen
ergeben sie eine Klasse einfacher Mo­
delle. Sie dürfen nur noch von der Zeit
abhängen, weil jede Ortsabhängigkeit
durch die angenommene Homogenität
ausgeschlossen wird. Zwei Gleichungen
bestimmen das Verhalten dieser Modell­
universen. Die eine, benannt nach dem
russischen Mathematiker Alexander
Friedmann, beschreibt, wie sich das Aus­
dehnungsverhalten des Universums im
Lauf der Zeit ändert. Die andere formu­
liert die Energieerhaltung, die in solchen
hochsymmetrischen Modellen unver­
meidlich ist. Wo es wegen der angenom­
menen Isotropie keine ausgezeichneten
Richtungen geben darf, kann auch keine
Energie fließen, denn jeder Energiestrom
würde eine Richtung markieren. Wenn
aber keine Energie fließen kann, muss sie
in jedem beliebigen Teilvolumen des Uni­
versums erhalten bleiben.
Die Friedmann-Gleichung zeigt, dass
der gesamte Materie- und Energieinhalt
versum vollzieht also folgende Schritte:
Allein maßgeblich für das Verhalten des
Universums ist die Gravitation, die wir
anhand der Allgemeinen Relativitätstheo­
rie beschreiben. Mit Hilfe der beiden Sym­
metrieannahmen, dass das Universum
nach geeigneter Mittelung um uns herum
isotrop sei, und dass es keine ausgezeich­
neten Beobachter im Universum gebe,
folgt aus Einsteins Feldgleichungen die
Friedmann-Gleichung. Zusammen mit
der Energieerhaltung beschreibt sie eine
Klasse einfacher kosmologischer Model­
le, die durch eine Reihe von Parametern
gekennzeichnet sind.
Damit stellen sich zwei Fragen: Sind
die­se Friedmann-Modelle tatsächlich in
der Lage, das Verhalten des Universums
zu beschreiben, und wenn ja, welche Para­
meterwerte kennzeichnen speziell unser
Universum? In jüngster Vergangenheit ist
es nicht nur gelungen zu zeigen, dass die
Friedmann-Modelle ein konsistentes Bild
von der Entwicklung des Universums lie­
fern, sondern auch, ihre wesentlichen Pa­
rameter mit vorher ungeahnter Genauig­
Der Materie- und Energieinhalt des Universums bestimmt,
ob und wie es sich ausdehnt oder zusammenzieht.
des Universums bestimmt, ob und wie es
sich ausdehnt oder zusammenzieht. Sie
zeigt insbesondere auch, dass ein solches
homogenes und isotropes Universum in
der Regel nicht statisch sein kann. Erst
ein Kunstgriff Einsteins, der zunächst von
einem statischen Universum überzeugt
war, erlaubte statische Modelle: Er führ­
te zu diesem Zweck die kosmologische
Konstante ein. Wir stellen heute fest, dass
wir sie brauchen, obwohl wir von einem
nicht-statischen Universum überzeugt
sind, und sie gibt uns gewaltige Rätsel auf.
Die Logik bei der Konstruktion phy­
sikalischer Modelle für das gesamte Uni­
keit festzulegen. Die Kosmologie hat jetzt
ein Standardmodell, das ihr einen festen
theoretischen Rahmen gibt.
Einsteins Spezielle Relativitätstheo­
rie hat gezeigt, dass eine Unterscheidung
zwischen Masse und Energie nicht sinn­
voll ist, weil beide zueinander äquivalent
sind. Dementsprechend entscheiden alle
Beiträge zur kosmischen Energiedichte
über die Entwicklung des Universums,
unabhängig davon, ob sie in Gestalt ge­
wöhnlicher Materie oder exotischer For­
men von Energie auftreten.
Zunächst muss die uns vertraute Ma­
terie eine Rolle spielen, die aus Protonen,
In Kürze
m Was wissen wir heute über den Aufbau und die Entwicklung unseres Universums? Aus der Allgemeinen Relativitätstheorie und zwei grundlegenden Symmetrieüberlegungen folgt eine Klasse von
einfachen Weltmodellen, FriedmannModelle genannt.
m Es zeigt sich, dass die Friedmann-Modelle ein konsistentes Bild von der Entwicklung des Universums liefern. Mehr
noch: Ihre wesentlichen Parameter lassen sich präzise festlegen. Damit ver-
fügt die Kosmologie nun über ein Standardmodell, das ihr einen festen theoretischen Rahmen gibt.
m Beobachtungen bestätigen die Vorhersagen dieses Modells – zum Beispiel,
dass sich das Universum ausdehnt. Aber:
Offenbar besteht das Universum nur zu
einem kleinen Teil aus Materie, wie wir
sie kennen. Es gibt zusätzlich Dunkle
Materie, die wir nicht sehen, und eine
Dunkle Energie, die unser Universum
immer schneller auseinandertreibt.
Sterne und Weltraum August 2007 39

flach
SuW
negativ
gekrümmt
Abb. 2: Ob das Universum räumlich flach ist wie unser gewohnter Euklidischer Raum, oder
positiv bzw. negativ gekrümmt,
entscheidet die Gesamtdichte aller Arten von Energie oder Masse. Ist sie größer oder kleiner als
die kritische Dichte, ist der Raum
positiv oder negativ gekrümmt,
anderenfalls flach.
Galaxienflucht
und Hubble-Konstante
positiv
gekrümmt
Neutronen und Elektronen besteht, oder
aus anderen Elementarteilchen, die da­
mit verwandt sind. Wir bezeichnen sol­
che Materie als baryonisch. Sie tritt unter
anderem in Gestalt elektrisch geladener
Teilchen auf und wechselwirkt daher mit
Licht.
Weiterhin trägt alle Strahlung, die im
Universum enthalten ist, ebenfalls zur
kosmischen Energiebilanz bei. Beobach­
tungen, von denen noch die Rede sein
wird, zeigen uns, dass es darüber hinaus
noch Dunkle Materie gibt, von der wir
mit guten Gründen annehmen, dass sie
gar nicht mit Licht in Wechselwirkung
treten kann und vermutlich aus schwach
wechselwirkenden Elementarteilchen be­
steht. Schließlich kommt das kosmolo­
gische Standardmodell nicht ohne Ein­
steins kosmologische Konstante aus, für
die wir keinerlei wirklich befriedigende
Erklärung haben. Zur Unterscheidung
von der Dunklen Materie bezeichnen wir
den Beitrag der kosmologischen Kons­
tante auch als Dunkle Energie.
Universum räumlich flach, das heißt, die
von der Allgemeinen Relativitätstheorie
erlaubte Krümmung verschwindet dann
(Abb. 2). Üblicherweise werden also vier
Dichteparameter für den heutigen Zeit­
punkt angegeben, nämlich die Baryonen­
dichte Ωb0, die Dichte der Dunklen Mate­
rie Ωm0, die Strahlungsdichte Ωr0 und die
Energiedichte der kosmologischen Kons­
tante ΩΛ0. Sie und die Hubble-Konstante
gilt es zu bestimmen.
Diese vier Parameter, also die Energieoder Massendichten der baryonischen
Materie, der Strahlung, der Dunklen
Materie und der Dunklen Energie, be­
stimmen im wesentlichen das Ausdeh­
nungsverhalten des Universums. Wenn
wir sie kennen, wissen wir anhand der
Fried­mann-Gleichung und aufgrund der
Energieerhaltung, wie sich die Ausdeh­
nungsrate des Universums ändert. Um
ein Friedmann-Modell genau festzulegen,
brauchen wir als fünften Parameter noch
die Ausdehnungsrate zu einem bestimm­
ten Zeitpunkt, zum Beispiel heute. Sie
wird als Hubble-Konstante H0 bezeichnet
und sagt aus, um welchen relativen Betrag
sich beliebige Strecken im Universum pro
Zeiteinheit ändern.
Die kosmischen Energiedichten wer­
den gewöhnlich in Form dimensions­
loser Dichteparameter angegeben, indem
man sie auf eine kritische Dichte bezieht.
Wenn die Dichten aller Komponenten
des kosmischen Materials zusammen ge­
rade die kritische Dichte ergeben, ist das
Kurz nachdem Friedmann gezeigt hatte,
dass kosmologische Modelle im Rahmen
der Allgemeinen Relativitätstheorie in der
Regel nicht statisch sein können, sich also
ausdehnen oder zusammenziehen müs­
sen, zeigte Georges Lemaître, dass daraus
ein linearer Zusammenhang zwischen
den Fluchtgeschwindigkeiten benachbar­
ter Galaxien und ihrer Entfernung folgt
(siehe SuW 6/2007, S. 36). Lemaître führte
einen ersten Vergleich dieses Ergebnisses
mit Messungen durch, die der Amerika­
ner Vesto Slipher gesammelt hatte. Dem­
nach bewegen sich die meisten Galaxien
von uns weg, und zwar umso schneller, je
weiter sie von uns entfernt sind. Mit Hil­
fe erheblich verbesserter Daten bestätig­
ten Edwin Hubble und Milton Humason
schließlich Lemaîtres lineare Beziehung
(Abb. 3). Das war zunächst eine erste
Bestätigung der Friedmann-Modelle, er­
laubte aber auch eine Bestimmung der
Hubble-Konstante H0. Zwar ergab sich
ein viel zu großer Wert, aber wir verste­
hen heute, woher der Fehler kam.
Wenn sich das Universum jetzt aus­
dehnt, war es offenbar in der Vergangen­
heit kleiner als heute. Damit ist aber noch
nicht gesagt, dass es sich immer ausge­
dehnt haben muss. Insbesondere gibt es
Friedmann-Modelle, die, rückwärts in
der Zeit betrachtet, zunächst schrump­
fen, sich nach endlicher Zeit aber wie­
der ausdehnen und immer eine endliche
Größe behalten. Wir wissen aber anhand
sehr einfacher Beobachtungen, dass un­
ser Universum nicht von diesem Typ sein
kann. Daher ist in unserem Universum
der Schluss unvermeidlich, dass es einen
Urknall gegeben haben muss. Da unsere
physikalischen Theorien versagen, wenn
man sich dem Urknall theoretisch zu nä­
hern versucht, können wir nur feststel­
Quelle: Hubble und Humason 1931

40 Sterne und Weltraum August 2007
Abb 3: Die lineare Beziehung
zwischen der Fluchtgeschwindigkeit der Galaxien und ihrer
Entfernung, die Hubble und andere um 1930 fanden, wird als
Hubble-Gesetz bezeichnet. Die
Steigung der Beziehung ist die
Hubble-Konstante.
0.5
(
65
)
79
0.4
65
65
64
0.3
73
0.2
64
77 (Supernovae Ia)
79 (Supernovae II)
78 (Tully-Fisher-Relation)
91 (Fundamentalebene)
76 (Flächenhelligkeit
elliptischer Galaxien)
0.1
0

50
60
70
80
90
Hubble-Konstante H0 [(km/s)/Mpc]
Abb. 4: Im Rahmen des Hubble
Key Project wurde die HubbleKonstante mit Hilfe zahlreicher
verschiedener Entfernungsindikatoren gemessen. Genutzt wurden Supernovae der Typen Ia
und II, die Tully-Fisher-Relation
sowie die Fundamentalebene und
die Flächenhelligkeit von ellip­
tischen Galaxien. Die Graphik
zeigt die Wahrscheinlichkeitsverteilungen für den wahren Wert
von H0, der allen Messungen zu
Grunde liegen muss. Das ausgeprägte Maximum der Verteilung
definiert den heute besten Wert
von H0.
Quelle: Hubble Key Project
relative Verteilung der Wahrscheinlichkeitsdichte
km/s
H0 = (72 ± (3)r ± (7)s) –
Mpc

100
Abb. 5: Zusammen mit der Hubble-Konstante deutet bereits das
Alter des Universums darauf hin,
dass die Materiedichte kleiner als
die kritische Dichte sein muss.
Die beiden farbigen Bänder geben das Alter des Universums
für zwei verschiedene Modelluniversen an, eines mit und eines
ohne kosmologische Konstante.
Die Breite der Bänder ist durch
die Unsicherheit in der HubbleKonstante bestimmt. Wenn das
Universum etwa 13 Milliarden
Jahre alt sein soll, muss die Materiedichte weniger als die Hälfte
ihres kritischen Werts betragen.
20
18
räumlich flach, mit kosmologischer Konstante
16
14
12
10
M. Bartelmann
Alter [Milliarden Jahre]
len, dass dieser Urknall ein sehr heißer
und dichter Anfangszustand gewesen
sein muss, aus dem heraus sich das Uni­
versum entwickelte. Er muss eine end­
liche Zeit zurückliegen, die wir als das Al­
ter des Universums bezeichnen. Es kann
einfach durch den Kehrwert der HubbleKonstante abgeschätzt werden.
Obwohl das Prinzip einfach ist, lässt
sich die Hubble-Konstante sehr schwer
messen. Das liegt daran, dass Galaxien
nur im Mittel der Hubble-Geschwindig­
keit folgen, zusätzlich aber Eigenbewe­
gungen von einigen hundert Kilome­
tern pro Sekunde aufweisen. Erst bei ge­
nügend großen Entfernungen wird die
Hubble-Geschwindigkeit groß genug, um
diese Pekuliargeschwindigkeiten zu über­
treffen. Da die Hubble-Konstante aber das
Verhältnis aus der Geschwindigkeit und
der Entfernung der Galaxien ist, müssen
beide genau gemessen werden. Die Ge­
schwindigkeit ergibt sich einfach aus der
Rotverschiebung der Spektrallinien auf­
grund des Dopplereffekts, aber es ist sehr
schwer, große Entfernungen genau zu
bestimmen. Direkte Messungen sind nur
in unserer unmittelbaren Nachbarschaft
möglich und versagen darüber hinaus.
Die gängigsten Methoden beruhen auf
der kosmischen Entfernungsleiter, bei der
sekundäre Entfernungsindikatoren be­
nutzt werden.
Dazu gehört eine Klasse veränder­
licher Sterne, die Cepheiden. Das sind
Riesensterne in einem fortgeschrittenen
Stadium ihrer Entwicklung, die durch
eine Eigenart ihrer äußeren Schichten re­
gelmäßig pulsieren. Zwischen ihrer Pul­
sationsperiode und ihrer Leuchtkraft be­
steht eine Beziehung, sodass ihre wahre
Helligkeit ermittelt werden kann, indem
man die Periode misst. Aus dem Vergleich
mit der scheinbaren Helligkeit erhält man
dann die Entfernung. Dass die Cepheiden,
ebenso wie die mit ihnen verwandte Klas­
se der RR-Lyrae-Sterne, eine derartige Pe­
rioden-Leuchtkraft-Beziehung aufweisen,
war schon Hubble bekannt. Sie muss an­
hand naher Sterne geeicht werden, deren
Entfernung noch direkt gemessen werden
kann. Wenn es dann gelingt, solche Ster­
ne in fernen Galaxien zu finden, kann de­
ren Entfernung indirekt aus den Cephei­
den abgelesen werden. Natürlich braucht
man dazu Teleskope, die in der Lage sind,
entfernte Galaxien in Einzelsterne aufzu­
lösen. Mit zu diesem Zweck wurde das
Weltraumteleskop Hubble gebaut.
Es gibt etliche solcher Objektklassen,
die sich als sekundäre Entfernungsindi­
katoren eignen, weil ihre wahre Hellig­
keit aus anderen Beobachtungsgrößen
abgeleitet werden kann. Durch deren
gemeinsame Analyse gelang es im so ge­
nannten Hubble Key Project, die Hubble-
offen (negativ gekrümmt),
ohne kosmologische Konstante
8
0.1
0.2
0.3
0.4
0.5
0.6
0.7
Materiedichte-Parameter -M
0.8
0.9
1
Sterne und Weltraum August 2007 41

3He
(4
He
,D
)
p
4He
)
(n, D)
d
(d, p)
Das Alter des Universums
Unabhängig davon können wir das Min­
destalter des Universums auch anhand der
ältesten in ihm enthaltenen Objekte ab­
schätzen. Es ist sicher nicht jünger als die
Erde, das Milchstraßensystem oder ande­
re Himmelskörper, deren Alter wir durch
verschiedene Methoden bestimmen oder
zumindest eingrenzen können.
Das Alter der Erde lässt sich aus den
Häufigkeiten langlebiger Radioisotope
wie Uran-235 und Uran-238 ableiten, die
über verschiedene Zerfallsreihen und mit
verschiedenen Halbwertszeiten in sta­
biles Blei übergehen. Im Lauf der Zeit än­
dert sich also ihr Häufigkeitsverhältnis
auf charakteristische Weise. Zwar kennen
wir seinen anfänglichen Wert bei der Ent­
stehung der Erde nicht, aber er lässt sich
durch geeignete Kombination verschie­
dener Proben eliminieren. Auf diese Wei­
se findet man, dass die Erde etwa (4.6 ± 1)
Milliarden Jahre alt sein muss.
Das Prinzip dieser Methode lässt sich
auf das Milchstraßensystem ausdehnen,
indem man die Isotopenverhältnisse auf
der Erde mit denen vergleicht, die bei ih­
rem Ursprung in Supernova-Explosionen
erzeugt werden. Entsprechende Abschät­
zungen sind deswegen weniger genau,
weil nicht bekannt ist, wie sich die Häu­
figkeit von Supernovae im Verlauf der Ge­
schichte des Milchstraßensystems entwi­
ckelt hat. Verschiedene plausible Annah­
men führen auf Werte zwischen 7 und 13
Milliarden Jahre (Abb. 5).
Weitere Abschätzungen können
aus Kugelsternhaufen bzw. aus weißen
Zwergsternen gewonnen werden. Kugel­
sternhaufen gehören zu den ältesten Be­
standteilen des Milchstraßensystems und
42 Sterne und Weltraum August 2007
t
SuW
p
)
(d, n)
(d, n)
(p, D)
4 He
)
(d, p)
3He
,p
(n
Konstante mit einer zuvor unerreichten
Zuverlässigkeit zu bestimmen (Abb. 4).
Der gemessene Wert beträgt H0 = (72 ± 8)
(km/s)/Mpc. Ihrer Definition gemäß hat
die Hubble-Konstante die Dimension ei­
ner inversen Zeit. Ihr Kehrwert, 1/H0 =
(3.1 ± 0.3)·1017 s = 9.8 Milliarden Jahre,
liefert einen ersten Anhaltspunkt für das
Alter des Universums. Wenn es sich mit
konstanter Rate ausgedehnt hätte, hätte
es genau dieses Alter.
(p,

4He
SuW
n
7Li
(4
He
,D
d
7Be
)
1H
d
n
Abb. 6: Die Fusion von Helium
und weiteren leichten Elementen
setzt die vorherige Fusion von
Deuterium (schwerem Wasserstoff) voraus. Diese Erkenntnis
erlaubte Gamow die Vorhersage
der Temperatur des kosmischen
Mikrowellenhintergrunds.
,p
(n
1H
p
n
anderer Galaxien und enthalten etwa 105
Sterne, die jeweils annähernd gleichzei­
tig entstanden sind. Aus bestimmten be­
obachtbaren Eigenschaften dieser Stern­
populationen kann man rekonstruieren,
dass zumindest einige Kugelsternhaufen
ein Alter von etwa 13 Milliarden Jahren
haben müssen. Weiße Zwerge dagegen
sind die Endprodukte der Entwicklung
massearmer Sterne. Wenn deren Energie­
produktion versiegt, weil ihr Wasserstoff­
vorrat verbraucht ist, schrumpfen sie und
kühlen auf eine Weise aus, die theoretisch
gut verstanden ist. Zudem können Wei­
ße Zwerge keine größere Masse als etwa
1.4 Sonnenmassen haben. Zusammen
mit dem bekannten Kühlverhalten und
der beobachtbaren Helligkeitsverteilung
der Weißen Zwerge kann anhand dieser
oberen Massengrenze bestimmt werden,
wie alt die ältesten von ihnen sind. Damit
kommt man auf etwa (9.3 ± 2) Milliarden
Jahre für das Alter der Population Wei­
ßer Zwerge. Berücksichtigt man plausib­
le Abschätzungen der Zeit, die zwischen
dem Urknall und der Entstehung der ers­
ten Weißen Zwerge vergangen sein muss,
so erhält man daraus etwa (11 ± 2) Milliar­
den Jahre für das Alter des Universums.
Zusammen mit unserer Kenntnis der
Hubble-Konstante ergeben sich daraus
bereits sehr interessante Konsequenzen
für die Materiedichte im Universum.
Wäre sie hoch, so wäre die Ausdehnung
des Universums im Lauf seiner Entwick­
Abb. 7: Die relativen Häufigkeiten der leichten Elemente, die
kurz nach dem Urknall fusioniert
wurden, hängen nur vom Anzahl­
verhältnis der Baryonen und der
Photonen ab.
lung deutlich abgebremst worden. Die
heutige Expansionsrate, also die Hubb­
le-Konstante, wäre dann erheblich klei­
ner als früher. Daraus ergäbe sich dann
eine verhältnismäßig kurze Zeit seit dem
Urknall. Aus dem Alter des Universums
zusammen mit dem Wert der HubbleKonstante folgt also bereits eine obere
Beschränkung der kosmischen Materie­
dichte. Sie muss jedenfalls erheblich klei­
ner als die kritische Dichte sein, um das
Alter des Universums mit der HubbleKonstante in Einklang zu bringen.
Die Entstehung
der leichten Elemente
Eine Reihe weiterer wichtiger Schlussfol­
gerungen über das Universum beginnt
mit der Feststellung, dass die Masse des
baryonischen Materials zu etwa 25 Pro­
zent aus Helium besteht, was zum Bei­
spiel aus den Spektren von Sternen oder
dem interstellaren Gas bestimmt werden
kann. Woher kommt dieses Helium? Seit
den bahnbrechenden Arbeiten zur Ele­
mentfusion in Sternen von Hans Bethe
und Carl Friedrich von Weizsäcker Ende
der 1930er Jahre war erkennbar, dass es
durch Fusion in Sternen aus Wasserstoff
entstehen kann (siehe auch den Beitrag
auf S. 70 in diesem Heft). Schätzt man
aber die gesamte Heliummenge ab, die
seit der Entstehung des Universums durch
Sterne fusioniert werden konnte, so stellt
sich schnell heraus, dass dieser Mechanis­
2MASS
genau die richtige Menge Deuterium ent­
standen sein musste, um zu verstehen,
dass es heute im Universum weder null
Prozent noch 100 Prozent Helium gibt,
sondern etwa 25 Prozent. Wäre zu viel
Deuterium entstanden, so gäbe es heu­
te keinen Wasserstoff mehr, sondern nur
Helium. Wäre zu wenig Deuterium fusio­
niert worden, so gäbe es heute im wesent­
lichen Wasserstoff, aber kein Helium.
Daraus sowie aus einer Schätzung der
Baryonendichte im heutigen Universum
und den bekannten Wirkungsquerschnit­
ten der Fusionsreaktion von Wasserstoff
zu Deuterium konnte Gamow schließen,
dass die heutige Temperatur des Strah­
lungshintergrunds etwa fünf Kelvin be­
tragen müsse. Wäre sie geringer, so hätte
mehr Deuterium und Helium entstehen
müssen, und weniger, wenn sie höher ge­
wesen wäre. Ein Strahlungsfeld bei sol­
cher Temperatur hat seine größte Inten­
sität im Mikrowellenbereich. Auf diese
Weise konnte Gamow aus der HeliumHäufigkeit die Existenz eines kosmischen
Mikrowellenhintergrunds vorhersagen.
Von diesem und seiner außerordent­
lichen Bedeutung für die Kosmologie
wird später noch ausführlich die Rede
sein. Vorläufig betrachten wir die Entste­
hung des Heliums und anderer leichter
Elemente im frühen Universum näher.
Bereits etwa drei Minuten nach dem Ur­
knall war das Universum so weit abge­

mus keinesfalls ausgereicht haben kann,
um ein Viertel der kosmischen Gasmasse
in Helium zu verwandeln.
In den 1940er Jahren begann Geor­
ge Gamow, sich dieser Frage zu widmen.
Der russisch-amerikanische Physiker ver­
mutete, dass das Universum als Ganzes
das Helium erbrütet haben könnte. Dazu
musste es zunächst im frühen Universum
ausreichend heiß gewesen sein, damit Fu­
sionsprozesse ablaufen konnten. Im ther­
modynamischen Gleichgewicht bei sehr
hohen Temperaturen musste dann aber
auch eine thermische Strahlung entstan­
den sein, die zwar inzwischen ähnlich ab­
gekühlt sein musste wie das Universum
selbst, aber immer noch vorhanden sein
sollte. Gamow sagte also aus der Häufig­
keit des Heliums die Existenz eines gleich­
mäßigen Strahlungshintergrunds gerin­
ger Temperatur vorher (Abb. 6).
Gamow konnte noch einen wesent­
lichen Schritt weiter gehen. Da der Kern
eines Wasserstoffatoms aus einem einzel­
nen Proton, der Kern eines Helium­atoms
aber aus zwei Protonen und zwei Neu­
tronen besteht, müssten vier Teilchen
annähernd gleichzeitig aufeinandertref­
fen, um Helium zu fusionieren. Sehr viel
wahrscheinlicher ist aber ein Prozess,
in dem zunächst aus einem Proton und
einem Neutron ein Deuteriumkern und
dann aus zwei Deuteriumkernen ein He­
liumkern gebildet wird. Gamow sah, dass
Abb. 8: Galaxienhaufen wie der
Coma-Haufen enthalten einige
hundert bis etwa tausend Galaxien, die sich mit Geschwindigkeiten von etwa 1000 km/s bewegen. Um sie zu halten, benötigen sie sehr viel mehr als die
sichtbare Masse.
kühlt, dass Fusionsprozesse nicht mehr
in nennenswertem Umfang stattfinden
konnten. Während dieser sehr frühen
Phase spielten außer der elektromagne­
tischen Strahlung keine anderen Kom­
ponenten des kosmischen Materials
eine Rolle, einschließlich der kosmolo­
gischen Konstante. Für den Verlauf der
Elemententstehung war deswegen al­
lein das Anzahlverhältnis zwischen Ba­
ryonen und Photonen entscheidend. Die
Photonendichte und damit die Dichte der
Strahlungsenergie bestimmte die Aus­
dehnungsrate des Universums. Je größer
sie war, desto schneller expandierte das
Universum und kühlte sich ab. Demnach
stand für die Elemententstehung eine
umso kürzere Zeitspanne zur Verfügung,
je größer die Photonen- oder Strahlungs­
dichte war. Umgekehrt konnten umso
mehr Fusionsreaktionen ablaufen, je grö­
ßer die Baryonendichte war. Ein kleines
Baryon-zu-Photon-Verhältnis führte da­
her zu einer geringen Heliumhäufigkeit,
ein großes zu einer hohen.
Sterne und Weltraum August 2007 43
Rotationsgeschwindigkeit [km/s]
gemessen
200
100
berechnet
100000

MPIA, SuW
50 000
Abstand vom Zentrum [Lichtjahre]
Abb. 9: Die Umlaufgeschwindigkeiten der Sterne in Spiralgalaxien nehmen nach außen nicht
wesentlich ab, sondern bleiben
annähernd konstant. Die Massenverteilung der Galaxien muss
demnach sehr viel ausgedehnter
als ihre Lichtverteilung sein.

Abb. 10: Galaxien sind wesentlich größer, als sie optisch erscheinen. Neutraler Wasserstoff,
hier blau leuchtend dargestellt,
ist noch bei wesentlich größeren
Abständen vom Galaxienzentrum
zu finden als die Sterne. Die abgebildete Galaxie ist NGC 2915.
Neben dem gewöhnlichen Helium-4
entstanden weitere leichte Elemente, dar­
unter das bereits erwähnte Deuterium,
außerdem Tritium (überschwerer Was­
serstoff), Helium-3 und Lithium. Beson­
ders das Deuterium ist für die Analyse der
Nukleosynthese im frühen Universum
wichtig. Da es bei der Fusion des Heliums
und der weiteren Elemente verbraucht
wird, nimmt seine erwartete Häufigkeit
mit zunehmendem Baryon-zu-PhotonVerhältnis ab. Die erwarteten Element­
häufigkeiten wurden in großem Detail
numerisch berechnet (Abb. 7).
Durch eine ganze Reihe verschiedener
Beobachtungen können nun die Häufig­
keiten leichter Elemente bestimmt wer­
den. Dabei ist es sehr wichtig, dass mög­
lichst »primordiale« Gase beobachtet wer­
den müssen, die durch die spätere Fusion
in Sternen möglichst wenig verunreinigt
wurden. Besonders Absorptionslinien
des Deuteriums in den Spektren weit ent­
fernter Quellen haben sich dafür als sehr
nützlich erwiesen. Durch Vergleich der
beobachteten mit den theoretisch erwar­
teten Elementhäufigkeiten lässt sich dann
der einzige Parameter bestimmen, von
dem letztere abhängen, eben das Bary­
on-zu-Photon-Verhältnis. Da die Anzahldichte der Photonen aus Beobachtungen
des kosmischen Mikrowellenhinter­
grunds gut bekannt ist, kann schließlich
daraus die Dichte des baryonischen Ma­
terials im Universum abgeleitet werden.
Das Ergebnis ist, dass nur etwa vier Pro­
zent der kritischen Dichte aus baryo­
nischem Material bestehen.
Eso DSS2, blaues Overlay nach: G. R. Meurer, ApJ 111, 1551 (1996)
Dunkle Materie
44 Sterne und Weltraum August 2007
Bei weitem nicht das gesamte baryonische
Material, das aufgrund seiner elektrischen
Ladung elektromagnetisch wechselwir­
ken könnte, ist sichtbar. Wir schließen
auf seine Existenz nur indirekt aus den
Häufigkeitsverhältnissen der leichten Ele­
mente und, wie später noch zu beschrei­
ben sein wird, aus dem kosmischen Mi­
krowellenhintergrund. Was wir vor allem
in Sternen und diffusem Gas direkt zu
sehen bekommen, macht einen kleinen
Bruchteil davon aus.
Dass ein Großteil der Materie im Uni­
versum nicht sichtbar ist, wurde seit den
1930er Jahren erkennbar. Damals unter­
suchte Fritz Zwicky die Geschwindigkeit
der Galaxien im Coma-Galaxienhaufen
(Abb. 8). Galaxienhaufen wurden zu­
nächst als Gebilde identifiziert, in denen
auf recht engem Raum einige hundert Ga­
laxien konzentriert sind. Ihre Geschwin­
digkeiten längs der Sichtlinie lassen sich
anhand der Dopplerverschiebung von
Spektrallinien bestimmen. Zwicky fand,
dass sie im Bereich um 1000 km/s liegen.
Die Frage ist nun, wieviel Masse erfor­
derlich ist, um Galaxien zusammenzu­
halten, die sich mit solchen Geschwin­
digkeiten bewegen. Sind Galaxienhaufen
überhaupt Gebilde von Dauer, oder fin­
den sich in ihnen nur zufällig Galaxien
zusammen, um sich hernach wieder auf­
zulösen? Galaxienhaufen haben typische
Durchmesser im Bereich einiger Megaparsec, also einiger Millionen Lichtjahre.
Bei Geschwindigkeiten um 1000 km/s
braucht eine Galaxie etwa eine Milliarde
Jahre, um eine solche Strecke zu durch­
queren. Galaxienhaufen hätten sich im
Lauf der kosmischen Geschichte längst
aufgelöst, wenn sie nicht gebunden wä­
ren. Ein weiteres zwingendes Argument
dafür, dass Galaxienhaufen stabile Ob­
jekte sind, liefert das heiße Gas, mit dem
sie angefüllt sind und von dem später
noch die Rede sein wird.
GALILEO
/6‡-iÀˆi
£Î{ÓÊ
ÉnΙʀ
/6ÇÈÊvÉÈ]Î
ÊÓ£ÓäÊ
É£ÎÓxÊ€
/6nxÊvÉÇ
ÊÓnÎÓÊ
É£ÇÇäÊ€
/6£äÓ-ÊvÉn]È
{ÈÇÓÊ
ÉәÓäÊ€
*Ɉ-‡-iÀˆi
/6Èäˆ-ÊvÉÈ
ÓÈÎ{Ê
É£È{ÈÊ€
*‡£ä£ˆ-ÊvÉx]{
xÇșÊ
ÉÎÈäÈÊ€
*‡£ÓLj-ÊvÉx]Ó
£ä£ÈÇÊ
ÉÈÎxxÊ€
"ŽÕ>Ài\
>}iÀÊÓ]xʇʣΓ“
,>`ˆ>˜ÊÎʇʣn““
Unter etwas vereinfachenden Annah­
men kann man aus der Geschwindigkeit
der Galaxien und der Größe der Gala­
xienhaufen auf die Masse schließen, die
notwendig ist, so riesige Gebilde in einer
Art von Gleichgewicht zu halten. Zwicky
fand, dass der Coma-Haufen etwa 1015
Sonnenmassen enthalten muss. Das ent­
spricht der Masse von etwa 10 000 Gala­
xien, sichtbar sind aber »nur« etwa 1000.
Was verursacht diese große Diskrepanz?
Ihr
Woher kennen wir überhaupt die Mas­
se einzelner Galaxien? Das Argument
ist ähnlich dem, das wir für Galaxien­
haufen angewandt haben, nur beobach­
tet man die Bewegung der Sterne in den
Galaxien statt der Galaxien in den Gala­
xienhaufen. Spiralgalaxien mit ihrer aus­
geprägten Scheibenstruktur eignen sich
hervorragend, weil sie die plausible An­
nahme erlauben, dass die Sterne in ihren
Scheiben auf angenäherten Kreisbahnen
Astrospezialist
iÕÊLiˆÊ"
ʈ}…ÌÀˆ`}iʜLܘÃÊiÕÝi
n»]Ê£ä»]Ê£Ó»Ê՘`ʣȻ
/ii6Õi
/6ÈäÊvÉÈ
-
Eso DSS2, Overlay nach: H. Böhringer (MPIE) Rosat (1993)

Abb. 11: Die diffuse Röntgen­
emission des Coma-Galaxienhaufens ist hier in roten Schattierungen den optisch sichtbaren
Galaxien überlagert. Offenbar
füllt das heiße Röntgengas den
gesamten Galaxienhaufen aus.
iÊ{{ÇÊ
ÉÓǙʀ
iÊÎÈ{Ê
ÉÓÓnÊ€
iÀ˜}BÃiÀ\
œLܘʈ}…ÌÀˆ`}iÊiÕÝiÊ
ˆ˜ÊiˆV…Ì}i܈V…ÌÊ՘ÌiÀÊ`i˜ÊœLܘÌiiΜ«i˜°ÊiÃÌiÊ
“iV…>˜ˆÃV…iÊ6iÀ>ÀLiˆÌ՘}]ʅœ…iʜ«ÌˆÃV…iÊ+Õ>ˆÌBÌ]Ê
iˆ˜v>V…iÀÊ<ÕÃ>““i˜L>ÕÊ՘`ÊÃi…ÀÊ}ÕÌÊâÕÊÌÀ>˜Ã«œÀ̈iÀi˜°
>LÊ>}iÀʏˆiviÀL>À
ˆÌÌܓ“iÀ‡ŽÌˆœ˜Ê˜œV…ÊLˆÃÊ
âՓʣx°ÊՏˆÊÓääÇ
n¿¿ÊvÉÈ\
Çn£Ê
É{n™Ê€
£ä¸ÊvÉx\
£äΣÊ
ÉÈ{xÊ€
£Ó¿¿ÊvÉx\
£È¸vÉx\Ê
Ên]xÝ{Ó
ÓÇÈxÊ
É£Çәʀ
Ê£äÝ{Ó
ә£xÊ
É£nÓÓÊ€
£ÈÓÓÊ
É£ä£{Ê€
-
Ê£xÝxÈ7
ә£xÊ
É£nÓÓÊ€
ÎÈnnÊ
ÉÓÎäxÊ€
-
Ê£äÝxä7
Óx{äÊ
ɣxnnʀ
*œVŽiÌÊnÝÓäÊ
™ÎäÊ
ÉxnÓÊ€
-«iŽÌˆÛi\
Grüner Laserpointer
iˆÃÌ՘}ÃÃÌ>ÀŽiÀÊ՘`ÊÃi…ÀÊ}ÕÌÊ
-ˆV…iÀ˜Ê-ˆiÊÈV…ʘœV…ÊLˆÃÊâՓʣx°Ç°Ê ÈV…ÌL>ÀiÀ]Ê}ÀؘiÀÊ>ÃiÀ«œˆ˜ÌiÀ°Ê`i>Ê
vØÀʟvvi˜ÌˆV…iÊ؅À՘}i˜Êœ`iÀÊâՓÊ
LiˆÊiˆ˜i“Ê>ÕvÊØLiÀÊÓäääÊ
Ê
iˆ˜i˜ÊŽœÃÌi˜œÃi˜Ê>ÃiÀ«œˆ˜ÌiÀʜ`iÀÊ <iˆ}i˜ÊLiˆÊ/>}iψV…Ì°
149 CHF
iˆ˜Ê>ÀL‡ˆÌiÀÃiÌt
/-ÊÈxÊ
ÓÈÓäÊ
É£ÈÎnÊ€
/-Ênä
Ó{{xÊ
É£xәʀ
/-ÊnäÊ
ÎÈ{äÊ
ÉÓÓÇxÊ€
"ŽÕ>À>`>«ÌiÀ
£{™Ê
ə{Ê€
Ê
Ê
ADM - Argo Navis - ASA - Astrodon - Astronomik - AstroZap - Atik - Bob Knob's - Canon - Celestron - Cercis Astro - Coronado - Denkmeier - Diffraction Limited - Discovery - Equatorial Platforms - FLI - Gemini Geoptik - Importations Chinoises - Intes Micro - Johnsonian Design - Losmandy - Lumicon - Lymax - Meade - Miyauchi - Obsession - OGS - Optec - RCOS - RoboFocus - SBIG - Sirius Observatories - SkyWatcher
SolarScope - Software Bisque - Starlight Instruments - Starlight Xpress - StarryNight - StarWay - StellarCat - Swarovski - Takahashi - TEC - TeleVue - Vixen - William Optics
www.galileo.cc
[email protected]
Limmattalstrasse 206 - CH-8049 Zürich - Tel: +41 (0) 44 340 23 00 - Fax: +41 (0) 44 340 23 02
Rue de Genève 7 - CH-1003 Lausanne - Tel: +41 (0) 21 803 30 75 - Fax: +41 (0) 21 803 30 77
Preise inkl. 7.6% MWSt. Preise, Angaben und Abbildungen ohne Gewähr. Änderungen ohne Vorankündigung vorbehalten.

Abb. 12: Wenn Galaxien als Gravitationslinsen wirken, erzeugen
sie häufig Mehrfachbilder ferner
Quasare, wie hier das Vierfachbild des Quasars H 1413 (oben).
Der Gravitationslinseneffekt von
Galaxienhaufen erzeugt gelegentlich stark verzerrte, bogenförmige Bilder entfernterer Galaxien, wie hier im Galaxienhaufen
SDSS J1004+4112 (rechts).
46 Sterne und Weltraum August 2007
sind als Galaxien, ist ihre Anzahldichte
weit weniger genau zu bestimmen. Des­
halb geht man einen anderen Weg.
Galaxienhaufen sind groß genug, dass
man sie gegenüber ihrer Umgebung als
abgeschlossen betrachten kann. Es findet
also wenig oder kein Materieaustausch
mit ihrer Umgebung statt. Wenn das so
ist, sollte das Mischungsverhältnis aus ba­
ryonischer zu Dunkler Materie in Gala­
xienhaufen typisch für das gesamte Uni­
versum sein. Dann kann man aus dem
Verhältnis der Gesamtmasse der Galaxi­
enhaufen und der in ihnen versammelten
baryonischen Masse darauf schließen, wie
groß das Verhältnis aus gesamter zu bary­
onischer Materiedichte im Universum ist.
Da man aber die Dichte der baryonischen
Materie aus den Häufigkeitsverhältnissen
der leichten Elemente kennt, erhält man
daraus die Dichte der gesamten Materie.
Wie wiegt man
Galaxienhaufen?
Es ist prinzipiell einfach, aber praktisch
schwierig, die Menge der gesamten ba­
ryonischen Materie in Galaxienhaufen
zu messen. Zunächst kann man überle­
gen, wieviel baryonisches Material nö­
tig ist, um das Licht zu erzeugen, das die
Haufengalaxien abgeben. Bereits dieser
Schritt ist im Detail schwierig, weil er
einige Kenntnisse über den Aufbau, die
Entstehung und die Entwicklung der Ster­
ne voraussetzt. Ohne dies nachzuvollzie­
hen, nehmen wir hier an, dass wir solche
Kenntnisse in ausreichendem Maß ha­
ben. Damit können wir aus der gesamten
Leuchtkraft der Haufengalaxien die Men­
Esa, Nasa, K. Sharon (Tel Aviv University) und E. Ofek (Caltech)
stoffgases beobachtet, das im Radiobe­
reich bei 21 cm Wellenlänge ausgesandt
wird, stellt man fest, dass auch das Was­
serstoffgas bis zu sehr viel größeren Ab­
ständen vom galaktischen Zentrum sicht­
bar ist als die Sterne (Abb. 10). Die Um­
laufgeschwindigkeit dieses Gases eignet
sich ebenso wie die der Sterne dazu, die
Verteilung der Materie in Galaxien aus­
zumessen. Dabei stellt sich heraus, dass
die Umlaufgeschwindigkeiten auch dort
noch konstant bleibt, wo nur noch Was­
serstoffgas zu sehen ist, weit jenseits der
Bahnen der äußersten Sterne.
Wo enden also Galaxien? Vermutlich
erst dort, wo sie in ihre kosmische Um­
gebung abtauchen, wo also ihre langsam
abfallende Materiedichte sich der gleich­
mäßigen Dichte des Universums annä­
hert. Solche Überlegungen erlauben eine
einfache Abschätzung der gesamten Ma­
teriedichte im Universum. Anhand der
Geschwindigkeiten der Sterne und des
neutralen Wasserstoffs in Galaxien kön­
nen wir Galaxienmassen messen. Wenn
wir mittlere Galaxienmassen mit der An­
zahldichte der Galaxien multiplizieren,
also mit der Anzahl der Galaxien pro Vo­
lumen, ergibt sich eine mittlere Materie­
dichte. Sie liegt bei knapp zehn Prozent
der kritischen Dichte.
Kehren wir zu Galaxienhaufen zurück.
Im Prinzip ließe sich für sie dieselbe Rech­
nung durchführen wie für die Galaxien:
Das Produkt aus der typischen Masse
eines Galaxienhaufens und der mittleren
Anzahldichte solcher Galaxienhaufen er­
gibt eine Abschätzung der Massendichte.
Da Galaxienhaufen aber sehr viel seltener
CfA-Arizona Space Telescope Lens Survey
das Zentrum der Galaxie umlaufen. Wie­
der bestimmt man die Umlaufgeschwin­
digkeiten mittels Spektralanalyse und
schließt aus ihnen auf die Masse, die not­
wendig ist, um Sterne mit solchen Ge­
schwindigkeiten zu binden (Abb. 9).
Indem man Sterne mit wachsendem
Abstand vom galaktischen Zentrum un­
tersucht, kann man die Umlaufgeschwin­
digkeit in Abhängigkeit vom Radius aus­
messen. Tut man dies mit den Planeten
des Sonnensystems, das von der zentra­
len Masse der Sonne beherrscht wird,
so stellt man fest, dass die Geschwindig­
keiten nach außen hin abnehmen. Bei
Galaxien stellt sich heraus, dass die Um­
laufgeschwindigkeit der Sterne mit dem
Abstand vom Zentrum schnell zunimmt,
dann aber bis zu großen Entfernungen
mehr oder weniger konstant bleibt. Der
Vergleich mit dem Sonnensystem legt den
Schluss nahe, dass Galaxien nicht durch
eine zentrale Masse dominiert werden
können, sondern dass die gesamte Mate­
rie in ihnen sehr breit verteilt sein muss,
wesentlich breiter jedenfalls als das Licht,
das wir von den Galaxien sehen. Je weiter
man sich vom Zentrum einer typischen
Galaxie entfernt, desto größer wird offen­
bar das Verhältnis von nicht-leuchtender
zu leuchtender Materie.
Es ist nicht klar, wo Galaxien enden.
Die Verteilung ihres Sternlichts liefert of­
fenbar keinen guten Anhaltspunkt, weil
wir aus der Bewegung der Sterne wissen,
dass Galaxien auch dort noch beträcht­
liche Materiemengen enthalten, wo kei­
ne Sterne mehr zu sehen sind. Wenn man
Galaxien im Licht des neutralen Wasser­
ge der Baryonen bestimmen, die dafür be­
nötigt wird. Dabei stellt sich heraus, dass
die Baryonen in Sternen nur für wenige
Prozent der Haufenmasse aufkommen.
Galaxienhaufen sind aber starke Rönt­
genstrahler; sie sind sogar die stärksten
Röntgenquellen im Universum. Verant­
wortlich dafür ist heißes Gas, das die Ga­
laxienhaufen anfüllt, und das aufgrund
seiner hohen Temperatur weiche Rönt­
genstrahlung abgibt (Abb. 11). Aus der ge­
samten Röntgenleuchtkraft und der mitt­
leren Energie dieser Strahlung kann man
die Gesamtmasse dieses Röntgengases
abschätzen. Dabei stellt sich heraus, dass
es etwa zehn Prozent zur gesamten Hau­
fenmasse beiträgt und damit die Baryo­
nenmasse in Galaxienhaufen dominiert.
Nun kann man die vorhin angedeute­
te Rechnung zu Ende führen. Wenn etwa
ein Zehntel der Masse in Galaxienhaufen
baryonisch ist, wozu Sterne nur sehr we­
nig beitragen, und wenn dieses Verhält­
nis typisch für das gesamte Universum
ist, dann muss die gesamte Materiedichte
im Universum etwa das Zehnfache der
baryonischen Dichte betragen. Letztere
betrug etwa vier Prozent der kritischen
Dichte, also sollte die gesamte Materie­
dichte etwa 40 Prozent der kritischen
Dichte ausmachen. Genaue Rechnungen
bestätigen dies im Prinzip, kommen aber
auf Materiedichten um 30 Prozent der
kritischen Dichte.
Massenbestimmungen sind notorisch
schwierig, und die erwähnten kinema­
Literaturhinweise:
B. Majorovits,
H.-V. KlapdorKleingrothaus: Das Rätsel der Dunklen Materie, SuW 1/2000, S. 22 – 29
A. Burkert: Das Problem der
fehlenden Dunklen Materie, SuW
12/2000, S. 1055 – 1059
A. Burkert: Auf der Suche nach
Dunkler Materie in Elliptischen Galaxien, SuW 10/2006, S. 22 – 28
SuW Dossier 1/2006 »Struktur
des Kosmos«, Spektrum der Wissenschaft Verlagsges., ISSN 1612 4618
SuW Special 1/2006 »Unsere
kosmische Heimat – das neue Bild
der Milchstraße«, Spektrum der Wissenschaft Verlagsges., ISSN 1434
2057
M. Bartelmann 
Abb. 13: Gravitationslinsen sind
miserable abbildende Systeme,
wie hier am Beispiel der Mona
Lisa gezeigt. Aber gerade auf ihrem Astigmatismus beruht ihre
große Bedeutung für die Astrophysik.
tischen Methoden setzen mindestens vor­
aus, dass die betrachteten Objekte in einer
Art von mechanischem Gleichgewicht
sind. Hier kommt ein Effekt zu Hilfe, der
ebenso wie die gesamte Kosmologie auf
der Allgemeinen Relativitätstheorie be­
ruht. Bereits aus dem Äquivalenzprin­
zip, das der Konstruktion der Allgemei­
nen Relativitätstheorie zu Grunde liegt,
folgt, dass Licht von Gravitationsfeldern
abgelenkt werden muss, und zwar so,
dass Lichtstrahlen zu den ablenkenden
Massen hin gekrümmt werden. Dies ist
dem Verhalten optischer Sammellinsen
vergleichbar, weshalb man von Gravitati­
onslinsen spricht.
Von idealen optischen Linsen, denen
etwa Brillengläser sehr nahe kommen, er­
wartet man eine treue Abbildung, durch
die die betrachteten Gegenstände unver­
zerrt dargestellt werden. Dies ist bei Gra­
vitationslinsen nicht der Fall. Zwei be­
nachbarte Lichtstrahlen erfahren in aller
Regel verschiedene Ablenkwinkel, was
dazu führt, dass Objekte verzerrt erschei­
nen, die durch Gravitationslinsen abge­
bildet werden. In der gewöhnlichen geo­
metrischen Optik spricht man von Astig­
matismus (Abb. 13).
So störend der Astigmatismus op­
tischer Systeme sein kann, so wichtig ist
der Astigmatismus des Gravitationslin­
seneffekts. Wenn Gravitationslinsen treu
abbilden würden, könnten wir sie nicht
wahrnehmen. Erst ihr Astigmatismus
und die dadurch hervorgerufenen Bild­
verzerrungen verraten ihre Anwesenheit
und erlauben es, die Massenverteilungen
zu rekonstruieren, die als Gravitations­
linsen wirken. Wenn die Lichtablenkung
stark genug ist, kann sie dazu führen,
dass das Licht von einer einzelnen Quelle
auf verschiedenen Wegen zum Beobach­
ter gelangt. In einem solchen Fall sieht der
Beobachter die Quelle mehrfach abgebil­
det (Abb. 12).
Objekte ganz verschiedener Art kön­
nen als Gravitationslinsen wirken. Gala­
xien zum Beispiel können Mehrfachbilder
solcher Quellen erzeugen, die ausrei­
chend nahe an der Sichtlinie vom Beob­
achter durch das Zentrum der Galaxie
stehen. Dann treten typische Bildabstän­
de um eine Bogensekunde auf. Wenn die
Entfernungen vom Beobachter zur Gra­
vitationslinse und zur Quelle bekannt
sind, und wenn man plausible Modelle
für die Massenverteilung in Galaxien zu
Grunde legt, kann man aus der Größe der
Bildaufspaltungen auf die Masse der Ga­
laxien schließen. Dabei ist es unwichtig,
in welchem physikalischen Zustand sich
die Massenverteilung in den Galaxien
befindet, insbesondere ob sie im mecha­
nischen Gleichgewicht ist.
Auf ähnliche Weise erlaubt es der Gra­
vitationslinseneffekt, auch die Masse von
Galaxienhaufen zu bestimmen. Galaxi­
enhaufen, die als starke Gravitationslin­
sen wirken, können stark verzerrte, meist
bogenförmige Bilder solcher Galaxien
erzeugen, die vom Beobachter aus gese­
hen weit hinter ihnen stehen. Anhand der
Lage solcher Bögen relativ zum Haufen­
zentrum und ihrer Form lassen sich Mas­
senmodelle für Galaxienhaufen rekons­
truieren. Sowohl bei Galaxien als auch
bei Galaxienhaufen bestätigt der Gravita­
tionslinseneffekt die kinematischen Mas­
senbestimmungen. Von weiteren An­
wendungen des Gravitationslinseneffekts

wird später noch die Rede sein.
Im zweiten Teil: Kosmischer Mikrowellenhintergrund – Supernovae vom Typ Ia – Strukturen im Universum – Konsistenz in der Kosmologie – Inflation und Dunkle Energie.
Matthias Bartelmann ist Direktor
am Institut für Theoretische Astrophysik, einem der drei
Institute des Zentrums für Astronomie
der Universität Heidelberg, und Mitherausgeber von SuW.
Sterne und Weltraum August 2007 47