vierte Übungsblatt

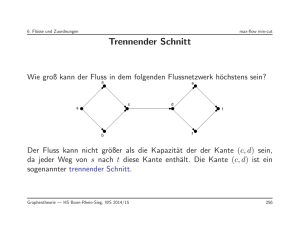
Institut für
Computergraphik und
Algorithmen
Abteilung für
Algorithmen und
Datenstrukturen
Sommersemester 2004
Übungen zur Lehrveranstaltung
Algorithmen und Datenstrukturen 2
4. Übungsblatt
Abgabe persönlich in der 4. Übung am 15.06.2004
Kreuzen Sie bitte in den Kästchen diejenigen Aufgaben an, bei denen Sie sich sicher sind, dass Sie die
richtige Lösung präsentieren können.
A1
A2
A3
A4
A5
A6
A7
A8
A9
A 10
kann präsentieren
Aufgabe 1 Maximale Flüsse – Ford-Fulkerson
Finden Sie zu dem nachfolgenden Flussnetzwerk N1 den maximalen Fluss f ∗ , indem Sie den Algorithmus
von Ford-Fulkerson verwenden:
t
15
3
20
3
5
7
1
9
4
2
12
10
8
s
a) Visualisieren Sie dazu die einzelnen Schritte des Algorithmus, d.h. Flüsse und Restgraphen.
b) Geben Sie anschließend einen Schnitt in N1 an, der von f ∗ saturiert wird.
Aufgabe 2 Maximale Flüsse – Edmond-Karp
Eine Variation des Algorithmus von Ford-Fulkerson verwendet augmentierende Pfade mit möglichst wenig
Kanten, d.h. zuerst werden die augmentierenden Pfade gesucht und anschließend wird entlang desjenigen Pfades mit minimaler Kantenzahl augmentiert. Diese Variation ist als Edmond-Karp-Algorithmus
bekannt.
1
a) Geben Sie den Edmond-Karp-Algorithmus in Pseudocode an.
b) Berechnen Sie den maximalen Fluss des Netzwerks N1 aus Aufgabe 1 und visualisieren Sie die
einzelnen Schritte in analoger Art und Weise.
Aufgabe 3 Maximale Flüsse
Welche der folgenden Behauptungen sind wahr und welche sind falsch? Belegen Sie Ihre Antwort entweder
durch ein Gegenbeispiel oder einen kurzen Beweis:
a) Seien v und w zwei beliebige Knoten in einem Flussnetzwerk N . In jedem maximalen Fluss f ∗ ist
entweder der Fluss von v nach w oder der Fluss von w nach v gleich 0.
b) Sei N ein Flussnetzwerk mit höchstens einer (gerichteten) Kante zwischen jedem Knotenpaar.
Wenn wir jede gerichtete Kante durch eine ungerichtete Kante ersetzen, dann bleibt der maximale
Fluss f ∗ unverändert.
c) Wenn zu allen Kantenkapazitäten eine beliebige positive Zahl λ addiert wird, dann wächst der
maximale Fluss um ein Vielfaches von λ.
d) Wenn zu allen Kantenkapazitäten eine beliebige positive Zahl λ addiert wird, dann ändert sich der
minimale Schnitt nicht.
Aufgabe 4 Maximale Flüsse
Konstruieren Sie drei Flussnetzwerke mit ganzzahligen Kapazitäten, die jeweils die folgenden Eigenschaften besitzen:
a) viele ganzzahlige maximale Flüsse und viele minimale Schnitte;
b) viele ganzzahlige maximale Flüsse und einen einzigen minimalen Schnitt;
c) einen einzigen maximalen Fluss und viele minimale Schnitte;
Aufgabe 5 Maximale Flüsse – Preflow-Push
Es sei ein weiteres Flussnetzwerk N2 mit ganzzahligen Kantenkapazitäten gegeben:
Berechnen Sie mit Hilfe des Preflow-Push-Algorithmus den maximalen Fluss von der Quelle s zur Senke
t. Zeichnen Sie die einzelnen Schritte des Algorithmus und geben Sie den Wert des maximalen Flusses
an.
2
Aufgabe 6 Matchings und Coverings
Gegeben sei ein bipartiter ungerichteter Graph G = (V, E) mit einer Knotenpartition V = L ∪ R und
L, R ⊆ V disjunkt. Alle Kanten in E liegen zwischen Knoten aus L und R. Ein Matching M ⊆ E ist
eine Teilmenge von Kanten aus E, so dass für alle Knoten v ∈ V höchstens eine Kante im Matching M
inzident zu v ist, d.h. keine zwei Kanten besitzen einen gemeinsamen Knoten. Ein maximales Matching
M ∗ ist ein Matching maximaler Kardinalität: es gilt also |M ∗ | ≥ |M | für jedes andere Matching M .
Ein Cover C ⊆ V ist eine Teilmenge von Knoten aus V , so dass jede Kante e ∈ E inzident zu mindestens
einem Knoten im Cover C ist. Ein minimales Cover C ∗ ist ein Cover minimaler Kardinalität: es gilt also
|C ∗ | ≤ |C| für jedes andere Cover C.
Zeichnen Sie zunächst einen Beispielgraphen und geben Sie ein Matching und ein Covering in diesem
Graphen an. Zeigen oder widerlegen Sie dann die folgende Behauptung: Für alle Cover C und alle
Matchings M gilt: |C| ≥ |M |.
Aufgabe 7 Matchings und Coverings
Ist G = (V, E) ein bipartiter Graph, so gilt für ein maximales Matching M ∗ und ein minimales Cover
C ∗ : |M ∗ | = |C ∗ |.
Beweisen Sie diese Behauptung, indem Sie das Problem als maximales Flussproblem formulieren.
Aufgabe 8 Geometrische Algorithmen – Scan-Line Prinzip
Seien P und Q konvexe Polygone in der Ebene mit n bzw. m Eckpunkten. Geben Sie einen effizienten
Algorithmus in Pseudocode an, der den Schnitt P ∩ Q in der Zeit O(n + m) mit Hilfe des Scan-Line
Prinzips berechnet.
Hinweis: Die Polygone P und Q sind gegeben als zirkuläre Liste ihrer Eckpunkte. Der Schnitt P ∩ Q ist
ebenfalls ein konvexes Polygon. Die gesucht Ausgabe ist die zirkuläre Liste der Eckpunkte von P ∩ Q.
Aufgabe 9 Geometrische Algorithmen – Sichtbarkeitsproblem
Wir betrachten das folgende Sichtbarkeitsproblem: Zwei horizontale Liniensegemente s und s0 in einer
gegebenen Menge horizontaler Liniensegmente S sind gegenseitig sichtbar, wenn es eine vertikale Gerade
gibt, die s und s0 , aber kein weiteres Liniensegment der Menge S zwischen den beiden Liniensegmenten
s und s0 schneidet. Es soll nun nach allen gegenseitig sichtbaren horizontalen Liniensegmentpaaren aus
der Menge S gesucht werden. Gehen Sie dabei von folgender vereinfachenden Annahme aus: Sämtliche
x-Werte von Anfangs- und Endpunkten aller Liniensegmente sind paarweise verschieden.
Geben Sie ein Beispiel des Problems mit 8 verschiedenen Liniensegmenten sowie die Lösung für Ihr
Beispiel an.
Aufgabe 10 Geometrische Algorithmen – Sichtbarkeitsproblem
Schreiben Sie unter Zuhilfenahme des Scan-Line Prinzips einen effizienten Algorithmus in Pseudocode,
der das Sichtbarkeitsproblem aus Aufgabe 9 für eine Menge von horizontalen Liniensegmenten löst.
Analysieren Sie die Laufzeit Ihres Algorithmus in O-Notation.
3