Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 4: Flüsse

Flüsse
Ferienkurs zur algorithmischen diskreten
Mathematik
Kapitel 4: Flüsse
Dipl-Math. Wolfgang Kinzner
3.4.2012
Dipl-Math. Wolfgang Kinzner
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 4:
Flüsse
Kapitel 4: Flüsse
Netzwerk, Fluss, s,t-Schnitt, Kapazität
MaxFlow-MinCut-Theorem
Restnetzwerk und Erhöhen des Flusswertes
Ford-Fulkerson-Algorithmus
Edmonds-Karp-Algorithmus
Dipl-Math. Wolfgang Kinzner
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 4:
Flüsse
Definition Netzwerk, Fluss, Wert des Flusses
Ein Netzwerk ist ein Tupel N = (V , A, s, t, c), wobei G = (V , A, c)
ein gerichteter Graph mit Kapazitätsfunktion c : A → R≥0 ist und
s, t ∈ V zwei ausgezeichnetene Knoten sind. Die Knoten s bzw. t
werden Quelle bzw. Senke genannt.
Eine Abbildung f : A → R≥0 heisst s-t-Fluss (engl. flow) in N,
wenn
X
X
f ((x , y )) ∀x ∈ V \{s, t} [Flusserhaltung],
f ((y , x )) =
y∈N − (x)
y∈N + (x)
f ((x , y )) ≤ c((x , y ))
∀(x , y ) ∈ A
Der Wert von f ist definiert als
X
f (s, y ) −
val(f ) :=
y∈N + (s)
[Zulässigkeit] .
X
f (y , s)
y∈N − (s)
Ein Fluss f hat maximalen Wert in N, falls val(f ) ≥ val(f ′ ) für
alle Flüsse f ′ in N gilt.
Dipl-Math. Wolfgang Kinzner
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 4:
Flüsse
Definition Schnitt, Kapazität
Eine Menge X ⊆ V mit s ∈ X und t ∈ V \ X heißt
s-t-Schnitt (engl. cut).
Die Kapazität von X ist definiert durch
cap(X ) :=
X
c(u, v )
u∈X ,v ∈N + (u)\X
Dipl-Math. Wolfgang Kinzner
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 4:
Flüsse
Zusammenhang Fluss-Schnitt
Wenn f ein Fluss und X ein s-t-Schnitt im Netzwerk N sind, dann
gilt
val(f ) ≤ cap(X ).
val(f ) =
P
x ∈X ,y ∈N +(x )\X
f (x, y ) −
MaxFlow-MinCut-Theorem:
max
f : Fluss in N
val(f ) =
Dipl-Math. Wolfgang Kinzner
P
x ∈X ,y ∈N − (x )\X
min
X : s-t-Schnitt in N
f (y , x)
cap(X )
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 4:
Flüsse
Übung 15 (MaxFlow-MinCut-Theorem)
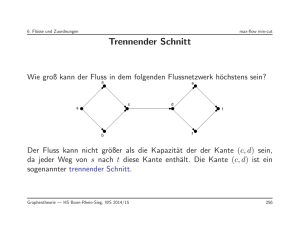
Bestimmen Sie einen minimalen Schnitt im folgenden Graphen.
Wie groß ist der maximale s,t-Fluss? Können Sie anhand eines
oder mehrerer minimaler Schnitte einen maximalen s,t-Fluss
bestimmen?
2
v1
2
5
s
v4
1
7
v3
3
4
4
t
5
6
6
v2
v5
3
Dipl-Math. Wolfgang Kinzner
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 4:
Flüsse
Restnetzwerk
Sei N = (V , A, s, t, c) ein Netzwerk und f ein Fluss in N. Das
Restnetzwerk von N bezüglich f ist definiert als
Nf := (V , Af , s, t, cf ), wobei wir zunächst die Kapazitätsfunktion
c mittels c(x, y ) := 0 für (x, y ) 6∈ A auf ganz V × V erweitern.
Dann setzen wir
cf (x, y ) :=


 c(x, y ) − f (x, y )
c(x, y ) + f (y , x)

 c(x, y )
falls f (x, y ) > 0
falls f (y , x) > 0
sonst
sowie Af := {(x, y ) : cf (x, y ) > 0}.
Dipl-Math. Wolfgang Kinzner
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 4:
Flüsse
Erhöhen des Flusswertes
Wenn f ein Fluss in N und W ein gerichteter s-t-Kantenzug
im Restnetzerk Nf ist, dann kann f entlang W zu einem Fluss
f ′ erhöht werden mit
val(f ′ ) = val(f ) + δ,
wobei 0 < δ := mine∈W cf (e).
Sei f ein Fluss in N. Wenn es in Nf keine s-t-Kantenzug mehr
gibt, dann hat f maximalen Wert.
Dipl-Math. Wolfgang Kinzner
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 4:
Flüsse
Algorithmus von Ford-Fulkerson
Input: Netzwerk N = (V , A, s, t, c)
Output: Fluss f
Ford-Fulkerson(N = (V , A, s, t, c))
(1) f := 0
(2) while ∃ s-t-Kantenzug W in Nf
(3)
erhöhe f entlang von W wie vorher beschrieben.
Dipl-Math. Wolfgang Kinzner
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 4:
Flüsse
Beispiel zum Ford-Fulkerson-Algorithmus
Folie 10
Dipl-Math. Wolfgang Kinzner
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 4:
Flüsse
Übung 16 (Ford-Fulkerson-Algorithmus)
Dipl-Math. Wolfgang Kinzner
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 4:
Flüsse
Übung 16 (Ford-Fulkerson-Algorithmus)
Dipl-Math. Wolfgang Kinzner
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 4:
Flüsse
Laufzeit und Probleme bei Ford-Fulkerson
Sei N ein Netzwerk mit Kapazitäten aus N0 . Dann terminiert
der Ford-Fulkerson-Algorithmus nach höchstens
P
(u,v )∈A c(u, v ) Schritten mit einem Fluss maximalen Werts.
Zwei Probleme können auftreten:
Der Algorithmus ist sehr langsam.
Im Falle nicht natürlicher Kapazitäten kann er eventuell gar
nicht oder gegen einen suboptimalen Fluss konvergieren.
Zwei mögliche Abhilfen:
Erhöhe in jeder
→ Algorithmus
Erhöhe in jeder
→ Algorithmus
Runde entlang des kürzesten s-t-Weges.
von Edmonds-Karp
Runde entlang aller kürzesten s-t-Wege.
von Dinic
Dipl-Math. Wolfgang Kinzner
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 4:
Flüsse
Algorithmus von Edmonds-Karp
Modifikation von Ford-Fulkerson:
Edmonds-Karp(N = (V , A, s, t, c))
(1) f := 0
(2) while ∃ s-t-Kantenzug W in Nf
(2’)
finde kürzesten s-t-Weg in Nf via Breitensuche
(3)
erhöhe f entlang von W um δ := mine∈W cf (e).
Laufzeit: O(|V | · |A|2 )
Dipl-Math. Wolfgang Kinzner
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 4:
Flüsse
Übung 17 (Edmonds-Karp-Algorithmus)
Die folgende Abbildung zeigt ein Netzwerk N mit seinen
Flusskapazitäten.
4
v1
6
5
8
s
6
v3
6
v4
7
3
t
5
v2
Benutzen Sie den Algorithmus von Edmonds-Karp, um einen
maximalen Fluss in N zu finden. Skizzieren Sie dazu die
entsprechenden Restenetzwerke und skizzieren Sie jeweils darin die
Breitensuche zum Finden eines augmentierenden Weges.
Dipl-Math. Wolfgang Kinzner
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 4:
Flüsse
Übung 18 (Diskrete Tomographie und Edmonds-Karp)
Es seien zwei Folgen (ai )i∈[n] , (bi )i∈[n] von natürlichen Zahlen
gegeben. Gesucht ist ein gerichteter Graph G = ([n], A), in dem
jeder Knoten i den Aus-Grad ai und den Ein-Grad bi hat.
Gegen sie ein polynomielles Verfahren an, das eine mögliche
Adjazenzmatrix von G berechnet oder feststellt, dass eine solche
nicht existiert.
Dipl-Math. Wolfgang Kinzner
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 4: