Übung 3 PDF - Informatik 4
Werbung

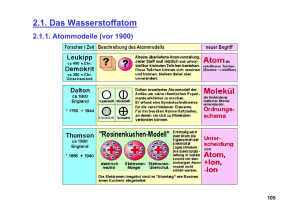
Rechnerstrukturen Sommersemester 2003 3. Übung Ausgabe 13.05.03 Abgabe 21.-23.05.03 Bei Fragen und Problemen können Sie uns per E-mail unter den folgenden Adressen erreichen: Mesut Güneş [email protected] Ralf Wienzek [email protected] Daniel Keysers [email protected] Aufgabe 1 (2+2+2+2+4=12 Punkte): Normalformen Gegeben sei die Boolesche Funktion f (x1 , x2 , x3 ) = (x1 + x2 + x3 ) · (x1 + x2 + x3 ) · (x1 + x2 + x3 ) a) Stellen Sie die Funktionstabelle auf und bestimmen Sie die einschlägigen Indizes! b) Bestimmen Sie die DNF von f ! c) Bestimmen Sie die KNF von f ! d) Bestimmen Sie die KRE von f ! e) Die Boolesche Funktion g = g(x1 , x2 , . . . , xn ) : B n → B habe genau i einschlägige Indizes, d.h. g liefere für genau i der 2n möglichen Belegungen der Variablen eine 1 als Funktionswert (0 ≤ i ≤ 2n ). Geben Sie eine einfache Regel in Abhängigkeit von i dafür an, ob der Term x1 · x2 · . . . · xn in der komplementfreien Ringsummenentwicklung von g vorkommt, sowie eine Begründung für diese Regel. Aufgabe 2 (3+3=6 Punkte): Boolesche Funktionen a) Sei f : B 13 → B die 13-stellige Boolesche Funktion mit f (x12 , x11 , . . . , x1 , x0 ) = 0 genau dann, wenn (x12 x11 . . . x1 x0 )2 durch 4711 teilbar ist. Geben Sie diese Funktion wahlweise in DNF oder KNF an. b) Wie viele 13-stellige Boolesche Funktionen gibt es? Zur Beantwortung dieser Frage bestimmen Sie zwei Zahlen m und d, sodass m · 10d die Anzahl der 13-stelligen booleschen Funktionen ist, 1 d eine ganze Zahl ist, und 10 ≤ m < 1 gilt. 1 Geben Sie m auf vier Nachkommastellen genau an. Aufgabe 3 (5 Punkte): Funktionale Vollständigkeit Ein System {f1 , . . . , fn } Boolescher Funktionen heißt funktional vollständig, wenn sich jede Boolesche Funktion durch Einsetzungen bzw. Kompositionen von Funktionen aus {f1 , . . . , fn } darstellen lässt. Zeigen Sie: {→, 0} ist funktional vollständig. Zur Erinnerung: x → y = x + y (und 0 ist die 0-stellige, konstante Funktion, die immer 0 liefert). m × 10d ist dann eine normalisierte Gleitkomma-Darstellung der Anzahl der 13-stelligen booleschen Funktionen. m heißt die Mantisse und d der Exponent dieser Darstellung zur Basis 10. 1 1 Rechnerstrukturen Sommersemester 2003 Aufgabe 4 (4+4+4+4=16 Punkte): Einfache Ein-/Ausgabe a) Das folgende Programm sehr_einfache_Ausgabe.mms gibt den Wert des Registers x als positive, ganze Zahl mit höchstens vier Stellen aus: Buffer x digit Main Loop BYTE " 0",#a,0 IS $14 IS $42 LOC #100 SET x,242 GETA $17,Buffer SET $18,3 DIV x,x,10 GET digit,rR ADD digit,digit,’0’ STBU digit,$17,$18 SUB $18,$18,1 BNZ x,Loop SET $255,$17 TRAP 0,Fputs,StdOut TRAP 0,Halt,0 vier Zeichen, newline, String-Terminator 0 get address of Buffer -> $17 $18 zaehlt die Stellen herunter 3...0 durch 10 teilen um die letzte Stelle als Rest zu erhalten der Rest der Division steht in rR -> digit addiere den Wert des ASCII Zeichens ’0’ store byte unsigned, schreibe das Zeichen in den Buffer mit dem Offset $18 (3...0) Offset herunterzaehlen branch if x not zero -> loop Adresse des Buffer in $255 laden String, auf den $255 zeigt, ausgeben Was passiert bei Zahlen, die dezimal mehr als vier Stellen benötigen? Wie kann man verhindern, dass außerhalb des Buffers geschrieben wird? Ändern Sie das Programm entsprechend ab. (Dabei sollen von allen Zahlen mit mehr Stellen nur die letzten vier Stellen ausgegeben werden.) b) Ändern Sie das Programm so ab, dass die Zahlen im Dualsystem ausgegeben werden. c) Ändern Sie das Programm so ab, dass auch negative Zahlen ausgegeben werden können. d) Das folgende Programm sehr_einfache_Eingabe.mms benutzt zwei verschiedene Arten zur Eingabe von Daten. Wenn ein Kommadozeilenparameter übergeben wird (z.B. durch mmix sehr_einfache_Eingabe Hallo), so wird der Programmname (der immer der erste Parameter ist) und der erste weitere Parameter ausgegeben. Ansonsten wird von StdIn (üblicherweise die Tastatur) eine Zeichenfolge gelesen und die ersten 7 Zeichen werden ausgegeben. Eingabe OCTA 0,8 Buffer newline BufAddr EinAddr Vergl Main BYTE " " BYTE #a,0 IS $42 IS $43 IS $41 LOC #100 CMP Vergl,$0,1 BP option1 GETA GETA STOU SET TRAP SET TRAP GETA Vergl,option2 BufAddr,Buffer EinAddr,Eingabe BufAddr,EinAddr,0 $255,EinAddr 0,Fgets,StdIn $255,BufAddr 0,Fputs,StdOut $255,newline Platz fuer die Uebergabe der Buffer-Adresse es sollen 8 Zeichen gelesen werden inkl. terminierender 0 an diese Stelle wird die Eingabe geschrieben ein newline-Zeichen mit String-Terminator compare, ist die Anzahl der Kommandozeilen-Parameter groesser als 1 (steht in $0) Wenn ja (Ergebnis positiv) gehe zu option2 sonst hier weiter, Adressen bestimmen Speichere die Adresse des Buffer bei ‘Eingabe’ Setze Register $255 Lies String von StdIn nach Buffer und gib ihn wieder aus 2 Rechnerstrukturen Sommersemester 2003 TRAP 0,Fputs,StdOut TRAP 0,Halt,0 option2 LDOU $255,$1,0 TRAP GETA TRAP LDOU 0,Fputs,StdOut $255,newline 0,Fputs,StdOut $255,$1,8 TRAP GETA TRAP TRAP 0,Fputs,StdOut $255,newline 0,Fputs,StdOut 0,Halt,0 gefolgt von newline lies die Adresse des ersten Kommandozeilen-Parameters in $255 ($1 zeigt darauf) und gib diesen aus die Adresse des zweiten Parameters steht 8 Byte weiter, lies sie ein ... Vollziehen Sie das Programm nach und schreiben Sie mit diesen Informationen ein Programm, das eine kleine, positive, ganze Zahl von StdIn einliest und die Zeichenkette Rechnerstrukturen ausgibt, wenn diese Zahl gleich 42 ist, sonst nichts tut. 3