2.1. Das Wasserstoffatom

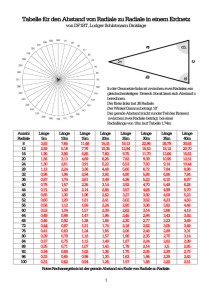
2.1. Das Wasserstoffatom
2.1.1. Atommodelle (vor 1900)
105
2.1.2. Eigenzustände des Wasserstoffatoms
Ein einfaches Beispiel: Wasserstoff in Wechselwirkung mit einem klassischen Feld.
Eigenenergien wasserstoffähnlicher Atome:
Klassisches Feld (monochromatische Lichtwelle):
Annahme: Die Frequenz des Lichtes ist in der Nähe der Übergangsfrequenz vom Übergang:
d.h.:
Für die Beschreibung des Systems müssen i.W. nur zwei Zustände berücksichtigt werden.
106
Die Eigenzustände des Wasserstoffatoms werden aus der stationären Schrödingergleichung
berechnet.
Allgemeines Problem (Zentralkraft):
reduzierte Masse
In Polarkoordinaten löst man die Gleichung durch einen Separationsansatz, d.h.:
Theorielehrbücher
Es ergeben sich 3 zu lösende Differentialgleichungen:
1) Azimutalgleichung (für Φ)
107
2) Polargleichung (für Θ)
3) Radialgleichung (für R)
Diese Separation gilt ganz allgemein für alle Zentralpotentiale V(r)!
Für physikalisch sinnvolle Lösungen (Verschwinden von ψ im Unendlichen;
Eindeutigkeit der Lösung; Quadratintegrierbarkeit) folgen gewisse Bedingungen
für die Separationskonstanten m und l:
m
magnetische Quantenzahl
l
Drehimpulsquantenzahl
108
Gleichzeitig gilt:
oder
Die normierten Funktionen
die die Winkelverteilung der Eigenfunktionen im Zentralpotential angeben,
heissen Kugelflächenfunktionen.
Spezielle Eigenschaften der Kugelflächenfunktionen:
a)
Orthonormalität
b)
Parität
109
Die Radialgleichung lässt sich zur besseren physikalischen Interpretation noch umformen:
mit:
folgt:
Man kann ein effektives Potential definieren:
Es besteht eine Analogie zur Rotationsenergie Erot eines klassischen Teilchens der Masse mr
um ein Zentrum im Abstand r:
mit dem Bahndrehimpuls
110
Aus der formalen Energie ergibt sich die „Mutmassung“:
oder
Quantenmechanischer Drehimpuls
Das Zentrifugalpotential
verschiebt das Minimum der radialen
Wellenfunktion zu größeren Abständen.
Veff
Das rechte Bild zeigt die Kombination
vom Zentrifugalpotential und von einem
Coulombpotential zu einem effektiven
Potential
∝
1
r2
radiale AufenthaltsWahrscheinlichkeit
r
∝−
1
r
111
Das Potentialminimum des effektiven Potentials Veff liegt bei:
mit
Man bezeichnet rl als den Bahnradius.
Spezialfall für das Wasserstoffatom
Radialgleichung:
Es folgt
Theorielehrbücher
Hauptquantenzahl
Drehimpulsquantenzahl
Magnetische Quantenzahl
112
Bemerkungen:
• Jeder Energieeigenwert ist n2-fach entartet.
• Die Unabhängigkeit der Energie von m folgt für alle Zentralpotentiale.
• Die Unabhängigkeit der Energie von l ist ein Spezialfall für das Coulombpotential!
Spektroskopische Notation:
ℓ
|m|
Zustand
Zustand
0
s
0
σ
1
p
1
π
2
d
2
δ
3
f
3
ϕ
4
g
4
γ
…
…
…
…
Beispiel: n = 4 , ℓ = 3 , m = −2
↔
4 f δ - Zustand
113
Einfaches Termschema des Wasserstoffs:
E
0
n=3
s
p
d
(ℓ=0)
(ℓ=1)
( ℓ = 2)
3s
3p
3d
3-fach entartet
−Ry*
n=2
2s
n=1
1s
5-fach entartet
2p
114
2.1.3. Der Drehimpuls
Hypothese: In Anlehnung an die klassische Physik lässt sich ein quantenmechanischer
Drehimpulsoperator für den Bahndrehimpuls aufschreiben:
Schreibweise als Determinante:
Somit in Analogie:
Drehimpulsoperator
115
Zusammenfassung der Eigenschaften des Bahndrehimpulsoperators
1) Der Bahndrehimpuls wird beschrieben durch den Operator
2) Die Eigenwerte von
sind
oder formal:
mit
3)
vertauscht mit
vertauscht nicht mit
und nicht mit
vertauscht nicht mit
und nicht mit
vertauscht nicht mit
und nicht mit
4) Die Eigenwerte der z-Komponente des Drehimpulsoperators
sind
mit
5) Die Drehimpulsquantenzahl l ist die Maximalkomponente des Drehimpulsoperators
gemessen in .
116
Darstellung des quantenmechanischen Drehimpulses im Kreiselmodell:
Beispiel: ℓ = 3
Kugelradius
= l (l + 1) h
m=3
m=2
z
y
m =1
m=0
x
m = −1
m = −2
m = −3
h
Ist eine
Quantisierungsachse
festgelegt (hier zRichtung) und
präpariert man das
quantenmechanische
System mit genau
bestimmter Projektion
auf diese Achse, so
sind die Komponenten
in der x- und yRichtung vollständig
unbestimmt, d.h. sie
liegen auf einem
Kreiskegel.
Bem: Auch für
maximale z-Projektion
(hier m=3) ist der
Drehimpuls nicht
parallel zur Z-Achse.
117
2.1.4. Diskussion der Wasserstoffwellenfunktion
Winkelverteilung
Die Winkelverteilung ist durch die Kugelflächenfunktionen bestimmt.
Die nachfolgende Abbildung zeigt eine Polardarstellung von
für die Hauptquantenzahl n=4.
Allgemeine Bemerkungen:
• Nur Zustände mit l=0 sind kugelsymmetrisch
• Die Winkelverteilung der quantenmechanischen (Wellen-)Lösung kann
als Projektion kreisförmiger Bewegungen eines klassischen Teilchens
interpretiert werden.
118
l=0 m=0
l=1 m=0
l=2 m=0
l=3 m=0
l=1 m=1
l=2 m=1
l=3 m=1
l=2 m=2
l=3 m=2
z
y
x
Bsp.: l=1, m=0
Im klassischen System zeige
der Drehimpuls z.B. in die
x-Richtung. Dies entspricht
einer klassischen Bewegung in
der z-y-Ebene. Eine Projektion
dieser Bewegung auf die z-xEbene liefert maximale
Aufenthaltswahrscheinlichkeit
an den Polen.
l=3 m=3
119
Radiale Verteilung
Zusammenstellung verschiedener Funktionen:
Radiale Wellenfunktion
Radiale Aufenthaltswahrscheinlichkeitsamplitude
Definition der radialen Aufenthaltswahrscheinlichkeitsdichte
:
gibt die Wahrscheinlichkeit an, das Elektron in einer Kugelschale
(Dicke dr) mit Radius r zu finden.
120
Allgemeine Bemerkungen zur radialen Wellenfunktion
:
• Kugelsymmetrische Zustände mit l=0 haben stets bei r=0 das Maximum der
radialen Wellenfunktion.
• Bei gösseren Drehimpulsquantenzahlen verschiebt das Zentrifugalpotential
das Maximum der radialen Wellenfunktionen zu grösseren Abständen.
• Die radiale Wellenfunktion kann auch durch die Anzahl der Knoten
charakterisiert werden.
Es ist:
Mittelwert von r
Bem.: Beim Bohrschen Radius ist
die Aufenthaltswahrscheinlichkeit
maximal. Im Mittel befindet sich das
Elektron aber im Abstand 1,5 a0 zum
Kern.
121
Radiale Aufenthaltswahrscheinlichkeiten der ersten drei Energieniveaus im Wasserstoffatom:
n = 1, ℓ = 0
nr = 0
n = 3, ℓ = 0
nr = 2
n = 3, ℓ = 1
nr = 1
n = 2, ℓ = 0
nr = 1
n = 3, ℓ = 2
nr = 0
n = 2, ℓ = 1
nr = 0
122
Gesamte räumliche Verteilung
Das Gesamtbild der räumlichen Verteilung ergibt sich durch Multiplikation der
Winkelverteilung mit der radialen Verteilung, d.h.
von
mit
Allgemeine Bemerkungen:
• Die Summe über alle magnetischen Quantenzahlen m für alle Stehwellen (zu einer
Drehimpulsquantenzahl l und einer Hauptquantenzahl n) ergibt stets eine
kugelsymmetrische Verteilung, d.h. die Wahl der Quanisierungsachse (meist z-Achse
genannt) ist irrelevant.
123
für die ersten beiden Zustände des Wasserstoffatoms
100
1s
200
2s
210
2p
211
2p
124
300
3s
310
3p
320
3d
311
3p
321
3d
für den Zustand n=3 des Wasserstoffatoms
322
3d
125
2.1.5. Zusammenfassung: Wellenfunktionen des H-Atoms
Die Winkelwellenfunktion
Normierungsfaktor
126
Die Radialwellenfunktion
assoziiertes Laguerre-Polynom
mit:
und:
= 0.529 Angstroem
127
2.1.6. Experimente mit einzelnen Atomen
Atomfallen
Einzelne Ladungen können nicht allein durch statische elektrische Felder stabil im Raum
gehalten werden (Earnshaw-Theorem).
Elektrische Wechselfelder (Paul-Falle)
Elektrische und magnetische Felder (Penning-Falle)
Eine Paul-Falle (Nobelpreis 1989) besteht aus zwei
parabolischen Elektroden und einer Ringelektrode:
128
Wird eine Gleichspannung Udc und eine Wechselspannung Vac mit der Frequenz Ω angelegt,
so hat das Potential nahe des Fallenzentrum die Form:
Wobei r0 und z0 den Abstand vom Fallenzentrum zu den Elektroden angibt.
Das Potential ist harmonisch und stellt für einen bestimmten Zeitpunkt eine
rücktreibende Kraft in einer Dimension dar:
129
Die Trägheit des gefangenen Teilchens verhindert, dass das Teilchen in der anderen
Richtung aus der Falle getrieben wird, bevor cos(Ωt) das Vorzeichen wechselt!
Für bestimmte Ω
rücktreibende Kraft in allen drei Raumrichtungen
Bewegungsgleichungen in der Paul-Falle:
Mit der Transformation:
130
folgt:
Mathieu‘sche Differentialgleichung
Falls
(gilt üblicherweise) ist die Lösung:
mit
Die Lösung besteht aus einer schnellen Bewegung der Frequenz ω (Mikrobewegung)
und einer langsamen Bewegung (Makrobewegung) in einem harmonischen Potential.
Im Fallenzentrum verschwindet die Mikrobewegung!
131
Experimentelle Realisierungen (Beispiel: Iontraps in Innsbruck, AG Blatt)
Linear
LinearIon
IonTraps
Traps
Courtesy: Rainer Blatt, University Innsbruck
Paul mass filter
Innsbruck
Ann Arbor
München
Boulder, Mainz, Aarhus
Innsbruck, Oxford
132
Innsbruck
Innsbrucklinear
linearion
iontrap
trap(2000)
(2000)
1.0 mm
6 mm
ω z ≈ 0.7 − 2 MHz
ω x , y ≈ 1.5 − 4 MHz
133
40
++ ions in a linear Paul trap
40
String
of
Ca
String of Ca ions in a linear Paul trap
row of qubits in a
linear Paul trap forms
a quantum register
70 µm
134
+
Level
Levelscheme
schemeof
ofCa
Ca+
qubit on narrow S - D
quadrupole transition
P3/2
854 nm
P1/2
866 nm
393 nm
D5/2
397 nm
D3/2
729 nm
S1/2
135
Spectroscopy
Spectroscopywith
withquantized
quantizedfluorescence
fluorescence(quantum
(quantumjumps)
jumps)
P
D
monitor
spectroscopy
absorption and emission
cause fluorescence steps
(digital quantum jump signal)
S
detection efficiency:
99.85%
Fluorescence intensity
S
# of measurements
Anzahl
der Messungen
8
7
D-Zustand
besetzt SS-Zustand
D state occupied
state occupied
besetzt
6
5
4
3
2
1
D
time (s)
0
0
20
40
60
80
100
120
Zählrateper
pro 99 ms
ms
counts
136