76 12 Wasserstoffatom Die Aufenthaltswahrscheinlichkeit des

76
12 Wasserstoffatom
Die Aufenthaltswahrscheinlichkeit des Elektrons um den Kern des Wasserstoffatoms ist nicht isotrop.
Sie ist für höhere Nebenquantenzahlen winkelabhängig und fällt durch die asymptotische Lösung stets
exponentiell mit dem Kernabstand ab.
Für höhere Hauptquantenzahlen ergeben sich zum Teil komplizierte Verläufe.
Es muss zwischen den Ausdrücken der Aufenthaltswahrscheinlichkeit in kartesischen (x, y, z) und in Kugelkoordinaten (r, ϑ, ϕ) unterschieden werden. Im Folgenden soll die Radiale Aufenthaltswahrscheinlichkeitsdichte P (r) für die tiefsten Zustände diskutiert werden.
Da die Laguerrepolynome Haupt- und Nebenquantenzahl enthalten, ist auch P (r) von n und l abhängig:
2
Pnl (r) = r2 Rnl
(r)
Warum dieser Ausdruck nicht einfach das Betragsquadrat der Radialfunktion ist, wird weiter unten erläutert.
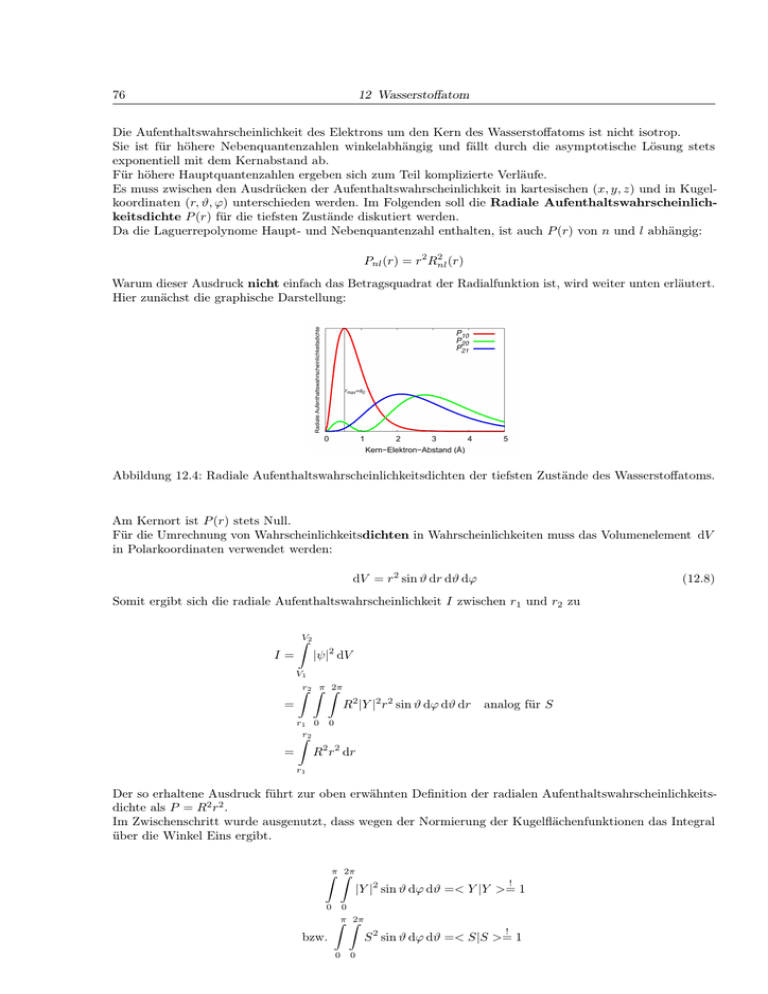
Hier zunächst die graphische Darstellung:
Abbildung 12.4: Radiale Aufenthaltswahrscheinlichkeitsdichten der tiefsten Zustände des Wasserstoffatoms.
Am Kernort ist P (r) stets Null.
Für die Umrechnung von Wahrscheinlichkeitsdichten in Wahrscheinlichkeiten muss das Volumenelement dV
in Polarkoordinaten verwendet werden:
dV = r2 sin ϑ dr dϑ dϕ
(12.8)
Somit ergibt sich die radiale Aufenthaltswahrscheinlichkeit I zwischen r1 und r2 zu
I=
ZV2
|ψ|2 dV
V1
=
=
Zr2 Zπ Z2π
r1 0
Zr2
R2 |Y |2 r2 sin ϑ dϕ dϑ dr
analog für S
0
R2 r2 dr
r1
Der so erhaltene Ausdruck führt zur oben erwähnten Definition der radialen Aufenthaltswahrscheinlichkeitsdichte als P = R2 r2 .
Im Zwischenschritt wurde ausgenutzt, dass wegen der Normierung der Kugelflächenfunktionen das Integral
über die Winkel Eins ergibt.
Zπ Z2π
0
bzw.
!
|Y |2 sin ϑ dϕ dϑ =< Y |Y >= 1
0
Zπ Z2π
0
0
!
S 2 sin ϑ dϕ dϑ =< S|S >= 1
77
12.2 Zeeman-Effekt
I(r) = P (r)dr ist damit die radiale Aufenthaltswahrscheinlichkeit des Elektrons innerhalb einer Kugelschale zwischen r und r + dr.
Davon zu unterscheiden ist die Aufenthaltswahrscheinlichkeit in einem kartesischen Volumenelement
dV = dx dy dz:
I(x, y, z) = |ψ(x, y, z)|2 dV
Das Volumenelement dV in kartesischen Koordinaten ist selbst keine Funktionen von x, y, z, daher ergibt
sich der einfachere Ausdruck.
Die kartesische Aufenthaltswahrscheinlichkeit hat für alle s-Orbitale ihr Maximum am Kernort.
12.1.2 Nomenklatur der Wasserstofforbitale
Die Symbole der Atomorbitale oder Wasserstofforbitale setzen sich zusammen aus dem Zahlenwert der
Hauptquantenzahl n, einem Symbol für die Nebenquantenzahl l, und einem Symbol für die Magnetquantenzahl
m (gemäß den reellen kartesischen Kugelflächenfunktionen) als Index:
Wert von l
Symbol
0
s
1
p
2
d
3
f
···
···
Damit ergibt sich explizit der folgende Zusammenhang zwischen den Zustandsfunktionen ψ und den aus der
Literatur bekannten einfachsten Atomorbitalen:
ψ100 ≡ 1s
ψ200 ≡ 2s
ψ210 ≡ 2pz
Die Übertragung ist jedoch für die komplexen Funktionen nicht einfach möglich:
ψ211 ≡ 2p1 6= 2px
ψ21−1 ≡ 2p−1 6= 2py
Die in der Chemie betrachteten Atomorbitale sind reelle Funktionen und müssen daher durch Linearkombinationen der komplexen Orbitale erzeugt werden.
Die Linearkombinationen führen die entsprechenden Transformationen von komplexen zu reellen Kugelflächenfunktionen durch (siehe 11.5).
1
2px = ψ211̄ = √ (ψ211 + ψ21−1 )
2
1
2py = ψ21−1̄ = √ (ψ211 − ψ21−1 )
i 2
12.2 Zeeman-Effekt
In den entsprechenden Experimenten wurde beobachtet, dass die entarteten Energieniveaus des Wasserstoffatoms mit m 6= 0 durch Anlegen eines äußeren homogenen Magnetfelds aufspalten.
~ angegeben (Einheit
Die Stärke eines Magnetfelds wird durch die sogenannte Magnetische Induktion B
Tesla T).
Die Wechselwirkung zwischen dem Elektron des Wasserstoffatoms und dem äußeren Magnetfeld wird dadurch
verursacht, dass die Kreisbewegung des Elektrons einen magnetischen Dipol erzeugt.
Der Dipolvektor m
~ L ist antiparallel zum Vektor des Drehimpulses.
m
~L=−
e ~
L
2me
Die Wechselwirkung zwischen dem vektoriellen Magnetfeld und dem magnetischem Dipol ergibt sich als
Skalarprodukt:
13.2 Erweiterung der Atomorbitale zu Spinorbitalen
79
nicht nach dem Korrespondenzprinzip aus der klassischen Mechanik herleiten. Er ergibt sich aber aus einer
relativistischen Behandlung im Rahmen der Dirac-Theorie. Hier soll der Elektronenspin als Erweiterung der
nichtrelativistischen Quantenmechanik behandelt werden.
In Analogie zur Wechselwirkung homogener Magnetfelder mit dem magnetischen Dipol wird der zusätzliche
Energiebeitrag empirisch wie folgt beschrieben:
Es = gβe ms Bz
dabei sind
g das gyromagnetische Verhältnis mit dem Wert ∼ 2, 002 für freie H-Atome
ms die Spinquantenzahl in Analogie zur Magnetquantenzahl
Es gibt aber einen fundamentalen Unterschied zwischen Drehimpuls und Spin:
Für Elektronen (Fermionen) gibt es nur einen Wert für den Spin: s = 12 (statt beliebiger natürlicher Zahlen
(und dem Wert Null) für l).
Damit gibt es wegen der analogen Beziehung |ms | ≤ s auch nur zwei erlaubte Werte für ms = − 21 und 12 .
Im Folgenden soll die bisher vorgestellte quantenmechanische Beschreibung des Wasserstoffatoms erweitert
werden.
13.2 Erweiterung der Atomorbitale zu Spinorbitalen
Die Wasserstofforbitale werden erweitert, indem sie mit einer sogenannten Spinfunktion, die nicht ortsabhängig ist, multipliziert werden.
Es ergeben sich die sogenannten Spinorbitale als Produkt von Orts- und Spinfunktion
ϕnlmms = ψnlm ηms
ψ ist eine Funktion von x, y, z oder r, ϑ, ϕ
η ist formal von der sogenannten Spinkoordinate σ abhängig
Auf die explizite Formulierung wird hier verzichtet, stattdessen wird im Folgenden eine einfache Form der
Spinfunktionen als Vektoren vorgestellt.
Da es nur zwei mögliche Werte für ms gibt, werden die entsprechenden Fälle speziell bezeichnet.
η 21 ≡ α
η− 12 ≡ β
↿ spin-up
⇂ spin-down
Beispiel: ϕ200 12 ≡ 2sα
13.3 Spinoperatoren
Sie werden analog zum Bahndrehimpuls definiert. Zunächst genügt es, die Wirkung auf die Spinfunktionen
zu zeigen:
Gesamtspin mit ~s = (sx , sy , sz )
3
ŝ2 α = ~2 s(s + 1) α = ~2 α
| {z }
4
r
p
3
|~s| = ~ s(s + 1) = ~
4
z }| {
3
ŝ2 β = ~2 s(s + 1) β = ~2 β
4
z-Komponente Operatorwirkung: ŝz ϕ = sz ϕ
80
13 Elektronenspin
1
~α
2
1
ŝz β = − ~β
2
ŝz α =
Der Spinoperator wirkt nur auf die Spinfunktion und nicht auf die Ortsfunktion.
ŝ2 ϕ = ŝ2 ψnlm ηms
= ψnlm ŝ2 ηms
= ψnlm ~s2 ηms
= ~s2 ϕ
Die Spinfunktionen sind keine Eigenfunktionen der anderen Komponentenoperatoren ŝx und sŝy .
Es ist wiederum günstiger, Leiteroperatoren einzuführen:
ŝ+ ≡ ŝx + iŝy
ŝ− ≡ ŝx − iŝy
)
ŝ2 = ŝ2x + ŝ2y + ŝ2z = ŝ+ ŝ− + ŝ2z − ~ŝz
ŝ+ α = 0 ŝ− α = ~β
ŝ+ β = ~α
ŝ− β = 0
13.4 Pauli-Spinmatrizen
Nach Pauli lassen sich die Spinoperatoren als 2 × 2-Matrizen und die Spinfunktionen als zweidimensionale
Einheitsvektoren darstellen.
1
0
α≡
β≡
0
1
~ 0 1
~ 0 −i
~ 1 0
ŝx ≡
ŝy ≡
ŝz ≡
2 1 0
2 i 0
2 0 −1
3
1 0
ŝ2 = ŝ2x + ŝ2y + ŝ2z = ~2
0 1
4
Orthonormierung der Spinfunktionen
Auch ohne explizite Angabe der Spinkoordinate (und damit der Vorgehensweise bei einer formalen Integration) lässt sich die Orthogonalitätsrelation der Spinfunktionen angeben. Hier entsprechen die folgenden
Erwartungswerte aber einfachen Skalarprodukten der Vektoren.
hα|αi = hβ|βi = αT α = 1
hα|βi = hβ|αi = β T β = 0
hα|βi = hβ|αi = 0
Damit sind die Spinorbitale über alle vier Quantenzahlen orthonormiert.
hϕnlmms |ϕn′ l′ m′ m′s i = δnn′ δll′ δmm′ δms m′s
(13.1)
13.5 Kommutatoren der Spinoperatoren
Analog zum Drehimpuls sind die Kommutatoren des Gesamtspinoperators mit den Komponentenoperatoren
null, die Kommutatoren der Komponentenoperatoren untereinander aber ungleich null:
ŝ2 , ŝz = ŝ2 , ŝx = ŝ2 , ŝy = 0
[ŝx , ŝy ] = i~ŝz etc.
82
13 Elektronenspin
i.A. ist der Gesamtdrehimpuls nicht die Summe der Einzelkomponenten, da er eine vektorielle Größe ist.
L 6=
n
X
li
i=1
Bei gegebener Gesamtwellenfunktion lässt sich der Gesamtbahndrehimpuls also analytisch berechnen. Für
viele Atome ist die Berechnung jedoch aufwändig.
Daher wurden Regeln für die möglichen Werte von L aufgestellt:
L = |ML |max , |ML − 1|, . . . , 0
13.7 Gesamtspin
Auch hier ist der n-Teilchenoperator der z-Komponente des Spinoperators Ŝz gleich der Summe der Einteilchenoperatoren, die wiederum nur auf je ein bestimmtes Elektron wirken:
Ŝz =
n
X
mit ŝz,i ϕa (i) = ~ms,a ϕa (i)
ŝz,i
i=1
mit Ms =
⇒ Ŝz Ψ = ~Ms Ψ
n
X
ms,a
a=1
~ ein Vektor ist.
Auch bei der Berechnung des Gesamtspins muss berücksichtigt werden, dass S
Ŝ 2 =
n
X
i=1
ŝ2i +
n
XX
(ŝx,i ŝx,j + ŝy,i ŝy,j + ŝz,i ŝz,j )
i6=j
⇒ Ŝ 2 Ψ = ~2 S(S + 1)Ψ
Analog zum Bahndrehimpuls lässt sich der Gesamtspin leichter über die Leiteroperatoren berechnen:
Ŝ 2 = Ŝ+ Ŝ− + Ŝz Ŝz − ~Ŝz
n
n
X
X
ŝ−,i
ŝ+,i , Ŝ− =
mit Ŝ+ =
i=1
i=1
Auch hier wird empfohlen, Ŝ+ Ŝ− Ψ als Ŝ+ (Ŝ− Ψ) durchzuführen.
Wie beim Gesamtbahndrehimpuls gilt allgemein, dass der Gesamtspin nicht die Summe der Einteilchenspins
ist
S 6=
n
X
sa
a
Nach einer Regel können nur folgende Werte von S vorkommen:
n n
0 gerades n
S = , − 1, . . . ,
1
ungerades n
2 2
2
Aus dem Gesamtspin lässt sich die Multiplizität von Spinzuständen berechnen:
M ≡ 2S + 1
Beispiel 17: Gesamtspin und Multiplizität für Zweielektronensysteme
ΨSpin
α(1)α(2)
β(1)β(2)
α(1)β(2) + α(2)β(1)
α(1)β(2) − α(2)β(1)
Ms
1
−1
0
0
S
1
1
1
0
M
3
3
3
1
Zustand
Triplett T
Singulett S