Modell: N unabhängige Spins – Binomialverteilung

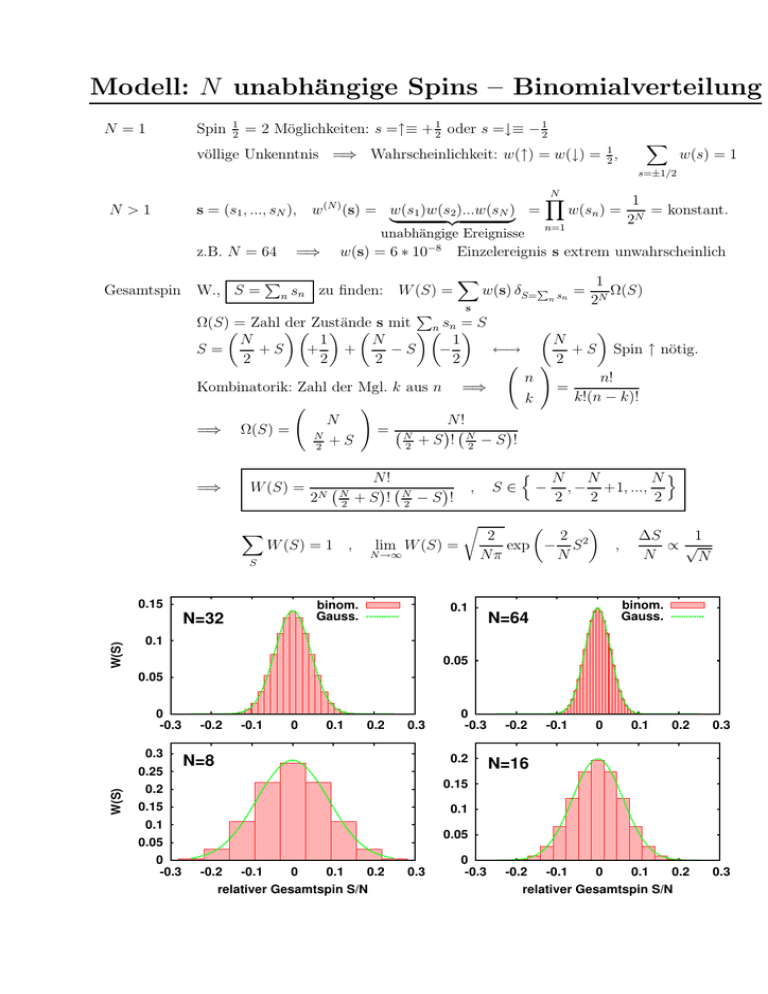
Modell: N unabhängige Spins – Binomialverteilung
N =1
Spin
1
2
= 2 Möglichkeiten: s =↑≡ + 21 oder s =↓≡ − 12
X
völlige Unkenntnis =⇒ Wahrscheinlichkeit: w(↑) = w(↓) = 21 ,
w(s) = 1
s=±1/2
N >1
s = (s1 , ..., sN ), w
(N )
(s) = w(s1 )w(s2)...w(sN ) =
|
{z
}
unabhängige Ereignisse
z.B. N = 64
Gesamtspin
W., S =
w(s) = 6 ∗ 10−8
=⇒
n sn zu finden: W (S) =
X
n
Kombinatorik: Zahl der Mgl. k aus n =⇒
k
!
N
N!
=⇒ Ω(S) =
=
N
N
N
+
S
!
−
S
!
+
S
2
2
2
W (S) =
X
2N
N
2
W (S) = 1 ,
N →∞
binom.
Gauss.
N=32
W(S)
−S !
lim W (S) =
S
0.15
N
2
n=1
w(s) δS=Pn sn =
s
P
Ω(S)= Zahl der
n sn =
s mit S
Zustände
N
1
1
N
+
←→
+S
+
−S
−
S=
2
2
2
2
=⇒
w(sn ) =
1
= konstant.
2N
Einzelereignis s extrem unwahrscheinlich
P
N!
+S !
N
Y
,
r
S∈
n
1
Ω(S)
2N
N
+S
!2
=
Spin ↑ nötig.
n!
k!(n − k)!
N
N
No
− , − +1, ...,
2
2
2
2
2 2
,
exp − S
Nπ
N
0.1
∆S
1
∝√
N
N
binom.
Gauss.
N=64
0.1
0.05
0.05
0
-0.3
0.3
W(S)
0.25
-0.2
-0.1
0
0.1
0.2
0.3
0
-0.3
0.2
N=8
0.2
0.15
0.15
0.1
0.1
-0.1
0
0.1
0.2
0.3
-0.1
0
0.1
0.2
0.3
N=16
0.05
0.05
0
-0.3
-0.2
-0.2
-0.1
0
0.1
0.2
relativer Gesamtspin S/N
0.3
0
-0.3
-0.2
relativer Gesamtspin S/N