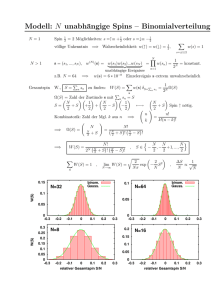
2.2 Wichtige Wahrscheinlichkeitsverteilungen Diskrete

2.2
2.2.1
Wichtige Wahrscheinlichkeitsverteilungen
Diskrete Verteilungen
Diskrete Gleichverteilung
Eine Menge M besteht aus n Elemente, die alle gleichwahrscheinlich sind.
Einzelwahrscheinlichkeit:
1
für k ∈ M
n
Momente für X ∼ U({1, 2, . . . , n}):
P (X = k) =
n+1
2
Anwendung: Laplace-Experiment
EX =
und
(Bez. : X ∼ U(M)).
VarX =
n2 − 1
12
Hypergeometrische Verteilung
Eine Menge besteht aus N Elementen. Dabei gibt es M von der Sorte 1 und N − M
von der Sorte 2. Aus der Menge werden n Stück (durch einmaliges Ziehen oder durch
Ziehen ohne Zurücklegen) gezogen. Die Zufallsgröße X ist die Anzahl der Stücke von
Sorte 1 unter den Gezogenen.
Einzelwahrscheinlichkeit:
¡M ¢ ¡N −M ¢
·
P (X = k) = k ¡N ¢n−k
k = max(0, n−(N −M )), . . . , min(n, M ) (X ∼ Hyp(N, M, n)).
n
Momente:
EX = n ·
M
N
und
VarX = n ·
M N −M N −n
·
·
N
N
N −1
Eigenschaften: Für N → ∞, M → ∞ und M
= p Übergang in eine BinomialverteiN
lung.
Anwendung: Sichprobennahme ohne Zurücklegen, Qualitätskontrolle
Beispiele:
X ∼ U({1, 2, 3, 4})
X ∼ Hyp(100, 40, 12)
8
Bernoulli-Verteilung
Bernoulli-Experiment: Experiment mit 2 möglichen Versuchsausgängen A oder Ac .
Das Ereignis A tritt dabei mit einer Wahrscheinlichkeit p = P (A) ein.
Tritt das Ereignis A ein, dann ist die Zufallgröße X gleich 1 und sonst gleich 0.
Einzelwahrscheinlichkeit:
P (X = 1) = p
und
P (X = 0) = 1 − p
(Bez. : X ∼ B(p)).
Momente:
EX = p
und
VarX = p · (1 − p)
Eigenschaften: Die Summe unabhängiger und identisch bernoulliverteilter Zufallsgrön
P
ßen ist Binomialverteilt: Xi ∼ B(p) i = 1, . . . , n =⇒
Xi ∼ Bin(n, p).
i=1
Binomialverteilung
Es werden n unabhängige Bernoulli-Experimente durchgeführt. Die Zufallsgröße X ist
gleich der Anzahl, wie oft das Ereignis A eintritt.
Einzelwahrscheinlichkeit:
µ ¶
n k
p (1 − p)n−k
P (X = k) =
k
k = 0, 1, . . . , n
(Bez. : X ∼ Bin(n, p)).
Momente:
EX = n · p
und
VarX = n · p · (1 − p)
Eigenschaften: Für n → ∞, p → 0 und n · p = λ Übergang in eine Poissonverteilung
Anwendung: unabhängige Wiederholung von Versuchen, Stichprobennahme mit Zurücklegen, Qualitätskontrolle, Schadenzahlverteilung in der Versicherungsmathematik
Beispiele:
X ∼ Bin(12, 0.4)
X ∼ Bin(100, 0.03)
9
Poissonverteilung
Einzelwahrscheinlichkeit:
P (X = k) =
λk −λ
·e
k!
λ > 0, k = 0, 1, . . .
(Bez. : X ∼ Poi(λ)).
Momente:
EX = λ
und
VarX = λ
Eigenschaften: Die Summe unabhängiger poissonverteilter Zufallsgrößen ist poissonm
P
P
verteilt: Xi ∼ Poi(λi ) i = 1, . . . , m =⇒
Xi ∼ Poi(λ) mit λ = m
i=1 λi .
i=1
Anwendung: Verteilung seltener“ Ereignisse, Bedienungstheorie, Qualitätskontrolle,
”
Schadenzahlverteilung in der Versicherungsmathematik
Beispiele:
X ∼ Poi(3)
X ∼ Poi(0.7)
10
Negative Binomialverteilung
Es werden unabhängige Bernoulli-Experimente solange durchgeführt bis zum r-ten mal
das Ereignis A eingetreten ist. Die Zufallsgöße X ist gleich der Anzahl der Versuche.
Einzelwahrscheinlichkeit:
µ
¶
k−1 r
P (X = k) =
p (1−p)k−r
k = r, r+1 . . .
(Bez. : X ∼ NegBin(r, p)).
r−1
Momente:
r
r(1 − p)
und VarX =
p
p2
Anwendung: Schadenzahlverteilung in der Versicherungsmathematik
EX =
Alternative Definition:
Die Zufallsgöße Y ist gleich der Anzahl der Versuchsausgänge Ac .
Also ist P (Y = k) = P (X = k + r) k = 0, 1 . . . und damit EY = EX − r =
r(1−p)
.
p
Geometrische Verteilung
Es werden unabhängige Bernoulli-Experimente solange durchgeführt bis zum ersten
Mal das Ereignis A eingetreten ist. Die Zufallsgöße X ist gleich der Anzahl der Versuche. (Spezialfall der Negativ-Binomialverteilung mit r = 1.)
Einzelwahrscheinlichkeit:
P (X = k) = p(1 − p)k−1
Momente:
k = 1, . . .
(Bez. : X ∼ Geo(p)).
1
1−p
und VarX =
p
p2
Eigenschaften: Verteilung ohne Gedächtnis“ (P (X = n + k|X > n) = P (X = k)).
”
Anwendung: Lauflänge bei Kontrollkarten (erwartete Lauflänge: ARL)
EX =
Beispiele:
X ∼ NegBin(5, 0.4)
X ∼ Geo(0.4)
11