M EF Rückblick: Trigonometrische Funktionen Mit - KGH auf lo-net

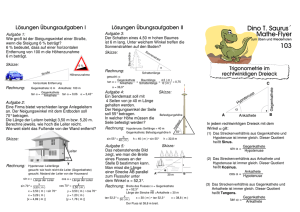
M EF
Rückblick: Trigonometrische Funktionen
Mit Hilfe des Sinus, Kosinus und Tangens werden Verhältnisse zwischen den Seitenlängen
in rechtwinkligen Dreiecken ausgedrückt:
Gegenkathete zu  a
=
Hypotenuse
c
Gegenkathete zu  b
sin =
=
Hypotenuse
c
sin =
Ankathete zu  b
=
Hypotenuse
c
Ankathete zu  a
cos =
=
Hypotenuse
c
cos =
Gegenkathete zu  a
=
Ankathete zu 
b
Gegenkathete zu  b
tan =
=
Ankathete zu 
a
tan =
Kotangens (Kehrwert des Tangens):
cot =
1
Ankathete zu 
b
=
=
tan  Gegenkathete zu  a
cot =
1
Ankathete zu 
a
=
=
tan  Gegenkathete zu  b
Es gilt:
sin 90 ° =cos 
tan 90 ° =−cot 
cos90 ° =−sin 
cot90° =−tan
Umkehrfunktionen
In manchen Situationen werden die trigonometrischen Winkelfunktionen benötigt, um aus
Seitenverhältnissen Winkel zu berechnen. Dazu werden die Arkusfunktionen arcsin, arccos,
arctan und arccot – die sogenannten Umkehrfunktionen zu den trigonometrischen
Funktionen – verwendet:
sin 30° =0,5⇒ arcsin 0,5=30 °
cos 60 ° =0,5⇒ arccos 0,5=60 °
tan 45 ° =1 ⇒arctan 1=45°
M EF
Rückblick: Trigonometrische Funktionen
Mit Hilfe des Sinus, Kosinus und Tangens werden Verhältnisse zwischen den Seitenlängen
in rechtwinkligen Dreiecken ausgedrückt:
Gegenkathete zu  a
=
Hypotenuse
c
Gegenkathete zu  b
sin =
=
Hypotenuse
c
sin =
Ankathete zu  b
=
Hypotenuse
c
Ankathete zu  a
cos =
=
Hypotenuse
c
cos =
Gegenkathete zu  a
=
Ankathete zu 
b
Gegenkathete zu  b
tan =
=
Ankathete zu 
a
tan =
Kotangens (Kehrwert des Tangens):
cot =
1
Ankathete zu 
b
=
=
tan  Gegenkathete zu  a
cot =
1
Ankathete zu 
a
=
=
tan  Gegenkathete zu  b
Es gilt:
sin 90 ° =cos 
tan 90 ° =−cot 
cos90 ° =−sin 
cot90° =−tan
Umkehrfunktionen
In manchen Situationen werden die trigonometrischen Winkelfunktionen benötigt, um aus
Seitenverhältnissen Winkel zu berechnen. Dazu werden die Arkusfunktionen arcsin, arccos,
arctan und arccot – die sogenannten Umkehrfunktionen zu den trigonometrischen
Funktionen – verwendet:
sin 30° =0,5⇒ arcsin 0,5=30 °
cos 60 ° =0,5⇒ arccos 0,5=60 °
tan 45 ° =1 ⇒arctan 1=45°
M EF
Einheitskreis:
Rückblick: Trigonometrische Funktionen