Dino T. Saurus´ Mathe

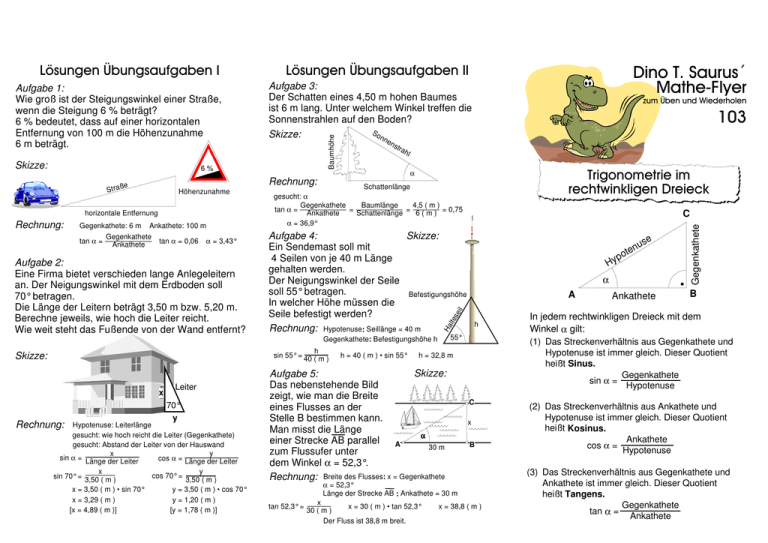
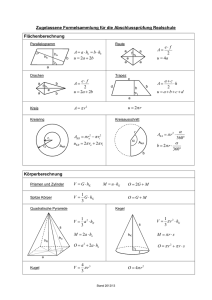
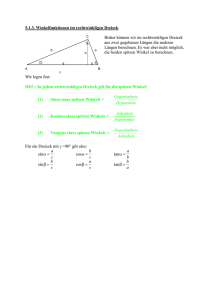
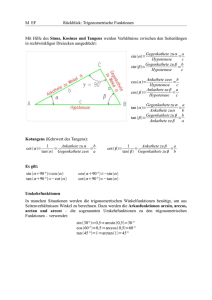
Skizze:
6%
tan a =
Ankathete: 100 m
Gegenkathete
Ankathete
tan a = 0,06
a = 3,43°
Aufgabe 2:
Eine Firma bietet verschieden lange Anlegeleitern
an. Der Neigungswinkel mit dem Erdboden soll
70° betragen.
Die Länge der Leitern beträgt 3,50 m bzw. 5,20 m.
Berechne jeweils, wie hoch die Leiter reicht.
Wie weit steht das Fußende von der Wand entfernt?
gesucht: a
4,5 ( m )
Gegenkathete
Baumlänge
tan a =
=
= 6 ( m ) = 0,75
Ankathete
Schattenlänge
a = 36,9°
x
Rechnung:
70°
y
Hypotenuse: Leiterlänge
gesucht: wie hoch reicht die Leiter (Gegenkathete)
gesucht: Abstand der Leiter von der Hauswand
x
y
sin a = Länge der Leiter
cos a = Länge der Leiter
y
x
cos 70° =
sin 70° = 3,50 ( m )
3,50 ( m )
x = 3,50 ( m ) • sin 70°
y = 3,50 ( m ) • cos 70°
x = 3,29 ( m )
y = 1,20 ( m )
[x = 4,89 ( m )]
[y = 1,78 ( m )]
Hy
h = 40 ( m ) • sin 55°
A
h
C
x
B
a = 52,3°
Länge der Strecke AB : Ankathete = 30 m
tan 52,3° =
x
x = 30 ( m ) • tan 52,3°
30 ( m )
Der Fluss ist 38,8 m breit.
se
Ankathete
B
In jedem rechtwinkligen Dreieck mit dem
Winkel a gilt:
(1) Das Streckenverhältnis aus Gegenkathete und
Hypotenuse ist immer gleich. Dieser Quotient
heißt Sinus.
Gegenkathete
sin a =
Hypotenuse
h = 32,8 m
Skizze:
Aufgabe 5:
Das nebenstehende Bild
zeigt, wie man die Breite
eines Flusses an der
Stelle B bestimmen kann.
Man misst die Länge
a
einer Strecke AB parallel
A
30 m
zum Flussufer unter
dem Winkel a = 52,3°.
Rechnung: Breite des Flusses: x = Gegenkathete
u
ten
po
a
55°
Gegenkathete: Befestigungshöhe h
Leiter
C
Aufgabe 4:
Skizze:
Ein Sendemast soll mit
4 Seilen von je 40 m Länge
gehalten werden.
Der Neigungswinkel der Seile
soll 55° betragen.
Befestigungshöhe
In welcher Höhe müssen die
Seile befestigt werden?
Rechnung: Hypotenuse: Seillänge = 40 m
h
sin 55° =
40 ( m )
Skizze:
Trigonometrie im
rechtwinkligen Dreieck
Schattenlänge
ei l
Gegenkathete: 6 m
103
l
lte
s
horizontale Entfernung
Rechnung:
str
ah
Ha
Höhenzunahme
en
zum Üben und Wiederholen
a
Rechnung:
e
Straß
Dino T. Saurus´
Mathe-Flyer
Aufgabe 3:
Der Schatten eines 4,50 m hohen Baumes
ist 6 m lang. Unter welchem Winkel treffen die
Sonnenstrahlen auf den Boden?
So
Skizze:
nn
Gegenkathete
Aufgabe 1:
Wie groß ist der Steigungswinkel einer Straße,
wenn die Steigung 6 % beträgt?
6 % bedeutet, dass auf einer horizontalen
Entfernung von 100 m die Höhenzunahme
6 m beträgt.
Lösungen Übungsaufgaben II
Baumhöhe
Lösungen Übungsaufgaben I
x = 38,8 ( m )
(2) Das Streckenverhältnis aus Ankathete und
Hypotenuse ist immer gleich. Dieser Quotient
heißt Kosinus.
Ankathete
cos a =
Hypotenuse
(3) Das Streckenverhältnis aus Gegenkathete und
Ankathete ist immer gleich. Dieser Quotient
heißt Tangens.
Gegenkathete
tan a =
Ankathete