sin-cos-tan

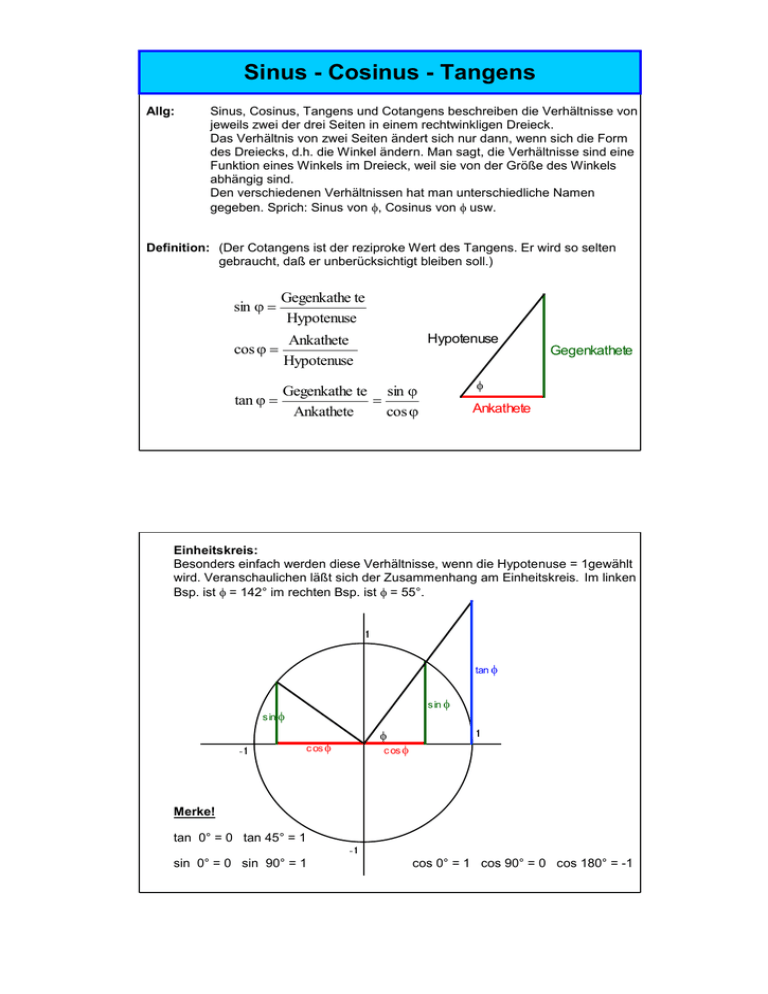
Sinus - Cosinus - Tangens
Allg:
Sinus, Cosinus, Tangens und Cotangens beschreiben die Verhältnisse von
jeweils zwei der drei Seiten in einem rechtwinkligen Dreieck.
Das Verhältnis von zwei Seiten ändert sich nur dann, wenn sich die Form
des Dreiecks, d.h. die Winkel ändern. Man sagt, die Verhältnisse sind eine
Funktion eines Winkels im Dreieck, weil sie von der Größe des Winkels
abhängig sind.
Den verschiedenen Verhältnissen hat man unterschiedliche Namen
gegeben. Sprich: Sinus von , Cosinus von usw.
Definition: (Der Cotangens ist der reziproke Wert des Tangens. Er wird so selten
gebraucht, daß er unberücksichtigt bleiben soll.)
sin  
Gegenkathe te
Hypotenuse
cos  
Ankathete
Hypotenuse
tan  
Gegenkathe te sin 

Ankathete
cos 
Hypotenuse
Gegenkathete

Ankathete
Einheitskreis:
Besonders einfach werden diese Verhältnisse, wenn die Hypotenuse = 1gewählt
wird. Veranschaulichen läßt sich der Zusammenhang am Einheitskreis. Im linken
Bsp. ist = 142° im rechten Bsp. ist = 55°.
tan 
s in 
s in 
c os 

c os 
Merke!
tan 0° = 0 tan 45° = 1
sin 0° = 0 sin 90° = 1
cos 0° = 1 cos 90° = 0 cos 180° = -1