¨Ubung zur Analysis 1 Blatt 12 Aufgabe 1. Der Tangens ist definiert

Prof. Dr. J. Ebert
PD Dr. T. Timmermann
Übung zur Analysis 1
Blatt 12
Abgabe bis Do, 22.01., 12 Uhr
Aufgabe 1 zur Bearbeitung in der Übung
Aufgaben 2-4 zur selbständigen Bearbeitung
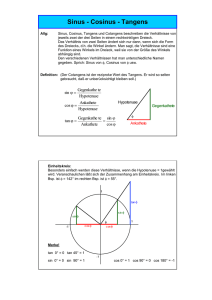
Aufgabe 1. Der Tangens ist definiert durch
tan : R \ {π(n + 21 ) : n ∈ Z} → R,
x 7→
sin x
.
cos x
Zeigen Sie:
(a)
lim tan(x) = −∞ und lim tan(x) = ∞ sowie tan((− π2 , π2 )) = R;
x&−π/2
(b) tan0 (x) =
monoton;
x%π/2
1
cos2 x
= 1 + tan2 x, und der Tangens wächst auf (− π2 , π2 ) streng
(c) der Tangens auf (− π2 , π2 ) hat eine differenzierbare Umkehrfunktion arctan : R →
1
(− π2 , π2 ), und arctan0 (x) = 1+x
2 für alle x ∈ R.
P∞
mit zn = xn + iyn ,
Aufgabe 2. (a) Eine Reihe komplexer Zahlen
P∞ n=0 zn P
xn , yn ∈ R, konvergiert
dann, wenn n=0 xn und ∞
n=0 yn konvergieren,
P∞ genau P
y
.
Zeigen
Sie,
dass
für
alle y ∈ R gilt:
und dann gegen n=0 xn + i ∞
n=0 n
∞
X
1
(iy)n = cos y + i sin y.
n!
n=0
P∞
P
Zahlen ist das Cauchy(b) Für zwei Reihen ∞
n=0 an und Pn=0 bn komplexerP
n
∞
Produkt definiert
n−k . Man kann
P∞ n=0 cn mit cn = k=0 ak bP
P∞ als die Reihe
zeigen: falls n=0 |an | und n=0 |bn | konvergieren, so auch n cn und es ist
! ∞ !
∞
∞
X
X
X
cn ,
bn =
an
n=0
n=0
n=0
siehe z.B. Forster, Analysis 1, S. 78. Zeigen Sie, dass für alle z, w ∈ C gilt:
! ∞
!
∞
∞
X wn
X
X
zn
(z + w)n
=
.
n!
n!
n!
n=0
n=0
n=0
(c) Zeigen Sie mit Hilfe von (a) und (b), dass für alle x, y ∈ R gilt:
ex (cos y + i sin y) =
∞
X
(x + iy)n
n=0
n!
.
Aufgabe 3. Zeigen Sie, dass die Funktion
(
x2 sin x12 , x 6= 0,
g : R → R, x 7→
0,
x = 0,
differenzierbar und ihre Ableitung g 0 auf [−1, 1] weder stetig noch beschränkt ist.
1
Prof. Dr. J. Ebert
Aufgabe 4.
PD Dr. T. Timmermann
(a) Zeigen Sie, dass die Dirichlet-Funktion
(
1, x ∈ Q,
χ : [0, 1] → R, x 7→
0, x 6∈ Q,
nicht Riemann-integrierbar ist.
für k = 0, . . . , n. Wir
(b) Sei f : [a, b] → R monoton, n ∈ N und xk = a + k b−a
n
definieren Treppenfunktionen g, h : [a, b] → R durch
g(a) = f (a) = h(a), g(x) = f (xk+1 ), h(x) = f (xk ) für x ∈ (xk , xk+1 ].
Zeigen Sie, dass
Z b
Z b
b−a
g(x) dx −
h(x) dx = |f (b) − f (a)|
n
a
a
und dass f Riemann-integrierbar ist.
Zusatzaufgabe 5. (a) Bezeichne S 1 := {(x, y) ∈ R2 : x2 + y 2 = 1} den Einheitskreis. Zeigen Sie, dass die Abbildung f : [0, 2π) → S 1 , t 7→ (cos t, sin t),
surjektiv ist.
(b) Zeigen Sie, dass die komplexe Exponentialfunktion z 7→ exp(z) ein surjektiver Homomorphismus der Gruppe (C, +) auf die Gruppe (C \ {0}, · ) ist
und den Kern {2πin : n ∈ Z} hat. (Hinweis: für x, y ∈ R gilt |ex+iy | = ex ,
hierbei bezeichnet |z| der Absolutbetrag von z ∈ C.)
2