Winkelfunktionen - brinkmann-du

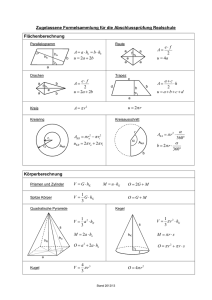
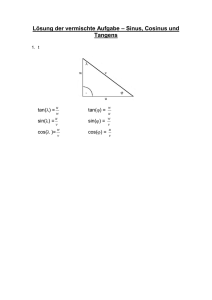
R. Brinkmann http://brinkmann-du.de
Seite 1
17.05.2009
Im rechtwinkligen Dreieck gilt für spitze Winkel α :
Gegenkathete
a
Sinus von
sin α =
α=
Hypotenuse
c
Ankathete
b
Cosinus von
cos α =
α=
Hypotenuse
c
Gegenkathete
a
Tangens von α =
tan α =
Ankathete
b
Ankathete
b
Cotangens von α =
cot α =
Gegenkathete
a
Zusammenhang mit dem Pythagoras:
Gegenkathete
Winkelfunktionen
e
us
n
e
t
po
Hy
α
Ankathete
B
c
a
c 2 = a2 + b2
( sin α )
2
+ ( cos α )
2
2
α
2
a2 + b2 c 2
⎛a⎞ ⎛b⎞
= ⎜ ⎟ +⎜ ⎟ =
= 2 =1
c2
c
⎝c⎠ ⎝c⎠
b
A
Beispiele:
1. Von einem Dreieck sind bekannt:
γ = 900 α = 340 c = 6 cm
gesucht sind die Seiten a und b.
a
sin α = ⇒ a = c ⋅ sin α a = 6 cm ⋅ sin 340 = 3,355 cm
c
b
cos α = ⇒ b = c ⋅ cos α b = 6 cm ⋅ cos 340 = 4,974 cm
c
C
C
900
b
a
α
A
c
B
2. Berechnen Sie die fehlenden Größen:
sin 50,80 =
11,4 cm
11,4 cm
⇒c=
= 14,711cm
c
sin 50,80
tan 50,80 =
11,4 cm
11,4 cm
⇒a=
= 9,298 cm
a
tan 50,80
11,4 cm
a
1
tan 50,80
tan α =
=
=
= 0,816 ⇒ α = 39,20
0
11,4 cm
11,4 cm
tan 50,8
Erstellt von R. Brinkmann bg_winkelfunktionen_01.doc
02.10.2007 20:16
C
,4
11
cm
α
A
900
a
50,8 0
c
Seite 1 von 1
B