Material zur Aufgabe

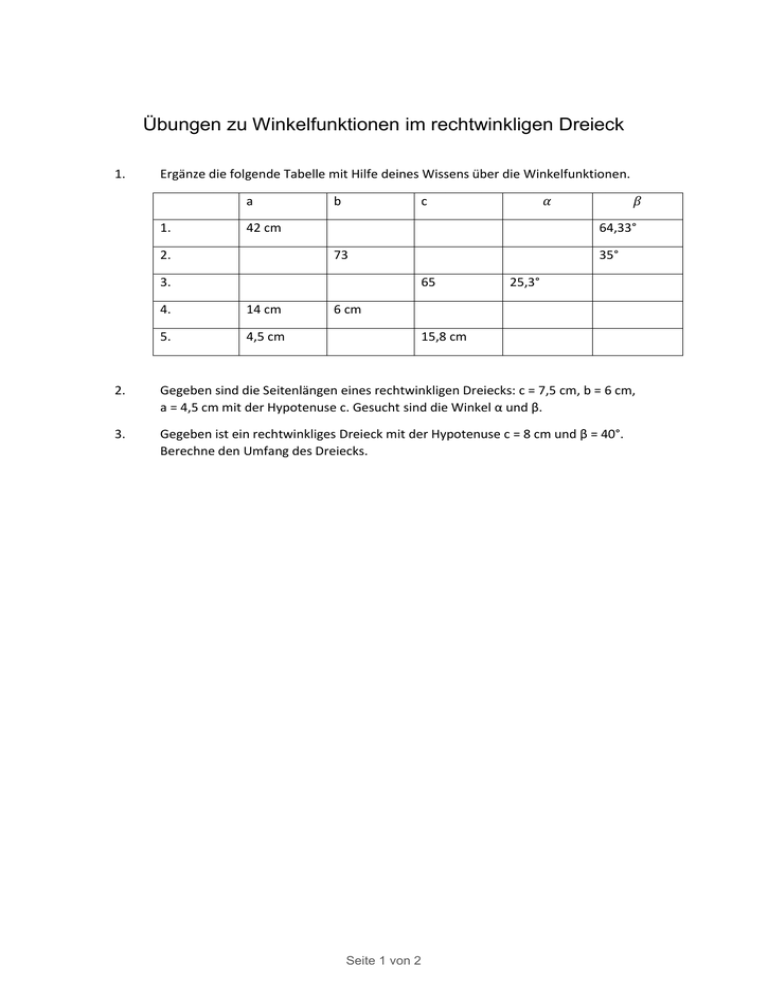
Übungen zu Winkelfunktionen im rechtwinkligen Dreieck
1.
Ergänze die folgende Tabelle mit Hilfe deines Wissens über die Winkelfunktionen.
a
1.
b
𝛼
c
42 cm
2.
64,33°
73
3.
35°
65
4.
14 cm
5.
4,5 cm
𝛽
25,3°
6 cm
15,8 cm
2.
Gegeben sind die Seitenlängen eines rechtwinkligen Dreiecks: c = 7,5 cm, b = 6 cm,
a = 4,5 cm mit der Hypotenuse c. Gesucht sind die Winkel α und β.
3.
Gegeben ist ein rechtwinkliges Dreieck mit der Hypotenuse c = 8 cm und β = 40°.
Berechne den Umfang des Dreiecks.
Seite 1 von 2
Beispiele für Produkte und Lösungen der Schülerinnen und Schüler
1.
𝛼
𝛽
a
b
c
1.
42 cm
87 cm
96,6 cm
25,67°
64,33°
2.
104,3
73
127,3
55 °
35°
3.
27,8
58,8
65
25,3°
64,7 °
4.
14 cm
6 cm
15,2 cm
66,8 °
23,3 °
5.
4,5 cm
15,2 cm
15,8 cm
16,6 °
73,4 °
2.
𝑎
4,5 𝑐𝑚
𝑐
7,5 𝑐𝑚
sin𝛼 = =
𝑏
6 𝑐𝑚
𝑐
7,5 𝑐𝑚
sin𝛽 = =
= 0,6 → sin-1 0,6 = 36,87°
= 0,8 → sin-1 0,8 = 53,13°
Man kommt zu den selben Ergebnissen, wenn man als Ansatz cos 𝛼, cos 𝛽, tan𝛼 oder
tan𝛽 nimmt.
3.
sin 𝛽 =
𝐺𝑒𝑔𝑒𝑛𝑘𝑎𝑡ℎ𝑒𝑡𝑒
𝐻𝑦𝑝𝑜𝑡ℎ𝑒𝑛𝑢𝑠𝑒
=
𝑏
8
𝑏
sin 40° = 8
b = 0,643 ∙ 8
b = 5,14 cm
𝑎
sin α = 8
sin 50° =
𝑎
8
a= 0,766 · 8
a = 6,13 cm
Der Umfang des Dreiecks: a+b+c = 6,13 cm + 5,14 cm + 8 cm = 19,27 cm
Zum gleichen Ergebnis gelangt man mit der Anwendung des Pythagoras.
Seite 2 von 2