) sin( )( x x xf ⋅= ) sin( )( x x xf −= ) cos( ) sin( 2)( x x xf − ⋅= cos 1)( x

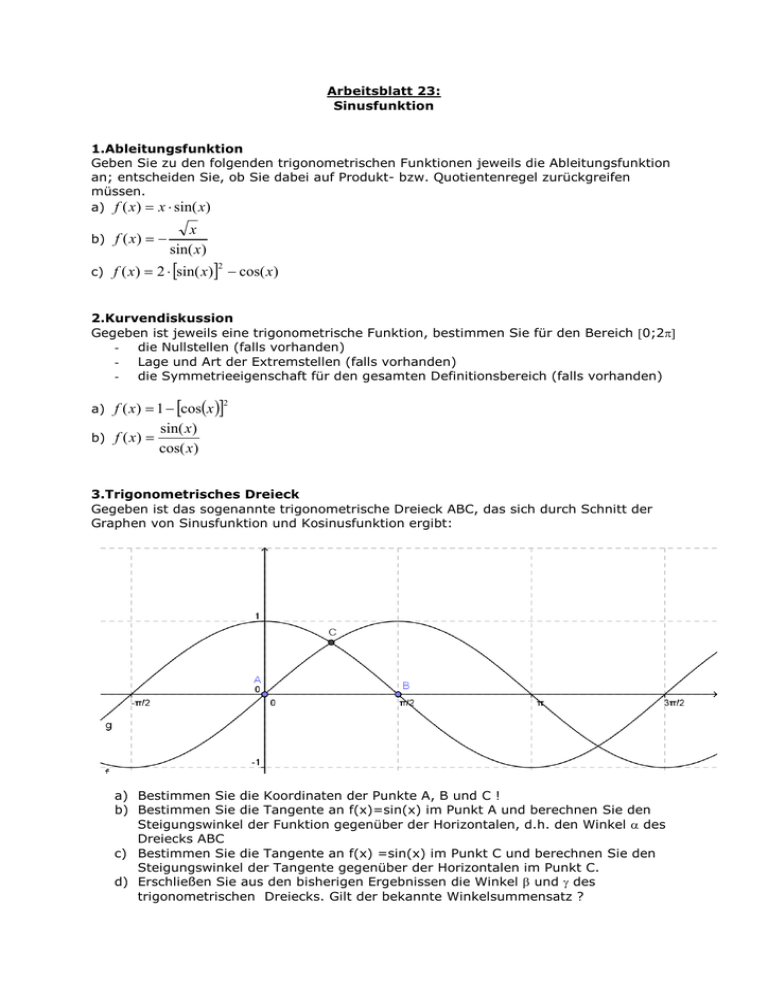
Arbeitsblatt 23:
Sinusfunktion
1.Ableitungsfunktion
Geben Sie zu den folgenden trigonometrischen Funktionen jeweils die Ableitungsfunktion
an; entscheiden Sie, ob Sie dabei auf Produkt- bzw. Quotientenregel zurückgreifen
müssen.
a) f ( x ) = x ⋅ sin( x)
x
sin( x)
b)
f ( x) = −
c)
f ( x) = 2 ⋅ [sin( x)] − cos( x)
2
2.Kurvendiskussion
Gegeben ist jeweils eine trigonometrische Funktion, bestimmen Sie für den Bereich [0;2π]
- die Nullstellen (falls vorhanden)
- Lage und Art der Extremstellen (falls vorhanden)
- die Symmetrieeigenschaft für den gesamten Definitionsbereich (falls vorhanden)
f ( x) = 1 − [cos(x )]
sin( x)
b) f ( x ) =
cos( x)
a)
2
3.Trigonometrisches Dreieck
Gegeben ist das sogenannte trigonometrische Dreieck ABC, das sich durch Schnitt der
Graphen von Sinusfunktion und Kosinusfunktion ergibt:
a) Bestimmen Sie die Koordinaten der Punkte A, B und C !
b) Bestimmen Sie die Tangente an f(x)=sin(x) im Punkt A und berechnen Sie den
Steigungswinkel der Funktion gegenüber der Horizontalen, d.h. den Winkel α des
Dreiecks ABC
c) Bestimmen Sie die Tangente an f(x) =sin(x) im Punkt C und berechnen Sie den
Steigungswinkel der Tangente gegenüber der Horizontalen im Punkt C.
d) Erschließen Sie aus den bisherigen Ergebnissen die Winkel β und γ des
trigonometrischen Dreiecks. Gilt der bekannte Winkelsummensatz ?