doc

Werbung

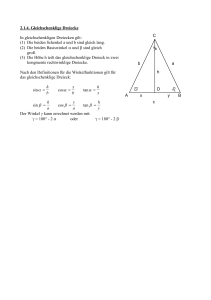
5.2.4. Flächeninhalt von Dreiecken
beliebige Dreiecke
1
ab sin 
2
1
A  ac sin 
2
A
1
bc sin 
2
1
A  gh g
2
A
rechtwinkliges Dreieck
A
1
ab
2
Dabei sind a und b die Seiten, die den rechten Winkel
bilden.
gleichseitiges Dreieck
A
a2
3
4

Herunterladen

Werbung

Random flashcards

2 Karten • oauth2_google_6c83f364-3e0e-4aa6-949b-029a07d782fb

Erstellen Lernkarten