Trigonometrische Funktionen am rechtwinkligen Dreieck

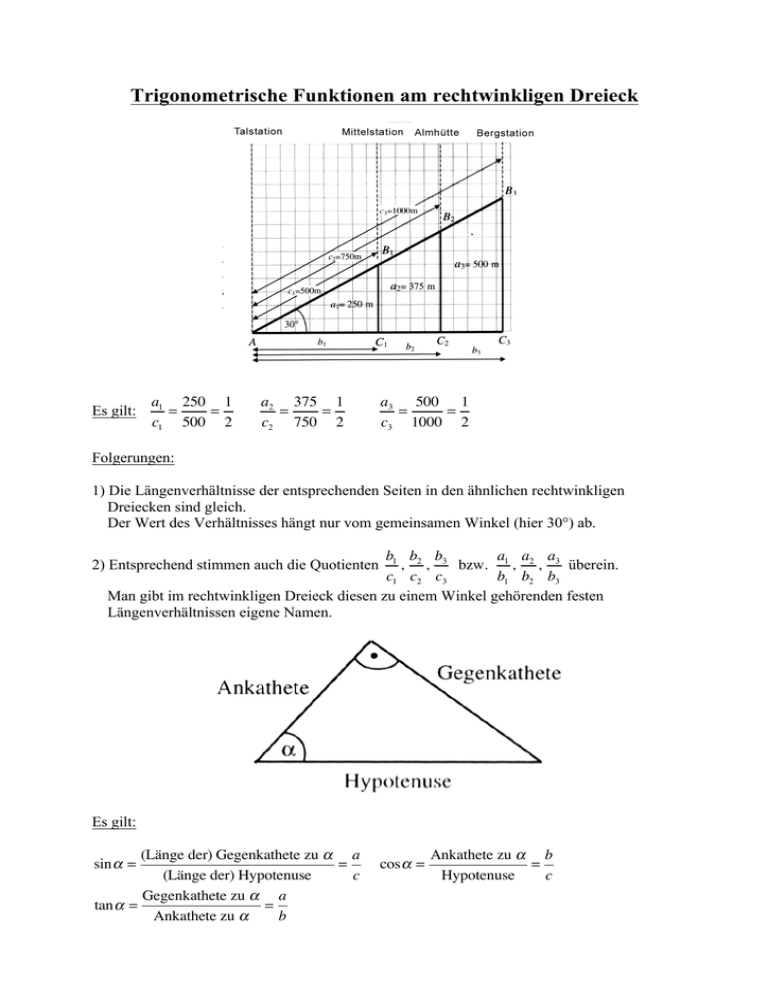
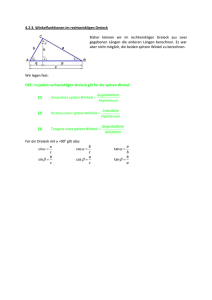
Trigonometrische Funktionen am rechtwinkligen Dreieck
Es gilt:
a1 250 1
=
=
c1 500 2
a2 375 1
=
=
c2 750 2
a3 500 1
=
=
c3 1000 2
Folgerungen:
1) Die Längenverhältnisse der entsprechenden Seiten in den ähnlichen rechtwinkligen
Dreiecken sind gleich.
Der Wert des Verhältnisses hängt nur vom gemeinsamen Winkel (hier 30°) ab.
b1 b2 b3
a a a
, , bzw. 1 , 2 , 3 überein.
c1 c2 c3
b1 b2 b3
Man gibt im rechtwinkligen Dreieck diesen zu einem Winkel gehörenden festen
Längenverhältnissen eigene Namen.
2) Entsprechend stimmen auch die Quotienten
Es gilt:
(Länge der) Gegenkathete zu α a
=
(Länge der) Hypotenuse
c
Gegenkathete zu α a
tan α =
=
Ankathete zu α
b
sin α =
cos α =
Ankathete zu α b
=
Hypotenuse
c
Beziehungen zwischen den Winkelfunktionen
sinα a b a
= : =
cosα c c b
b
= cos α
c
a
cos β = cos(90° − α ) = = sin α
c
sin β = sin(90° − α ) =
Aufgaben:
1. Berechnen Sie die fehlenden Stücke des folgenden Dreiecks (a = b), wenn a = 35m und
γ = 50°.
2. Bestimmen Sie, wie hoch ein Drachen steht, wenn die gespannte Schnur von 50m Länge
einen Winkel von 52° mit dem Erdboden bildet.
3. Ein Ballon mit dem Durchmesser 20m wird unter einem Sehwinkel ε = 0,4° beobachtet
(siehe untenstehende Skizze).
Berechnen Sie die Entfernung e des Ballons vom Beobachter B.
4. In einem gleichschenkligen Trapez sind die Grundseiten 10 cm und 6 cm lang, die
Schenkel 5 cm. Zeichnen Sie das Trapez und berechnen Sie die Maße der Innenwinkel
und die Maßzahl des Flächeninhalts.
1
5. Begründen Sie, dass für die Höhe im gleichseitigen Dreieck gilt: h = a 3
2
Lösungen:
1.
α + β + γ = 180° ⇒ 2α = 180° − γ ⇒ α = 65° = β
c
cosα = 1 ⇒ c1 = cos α ⋅ b = cos65°⋅ 35 ≈ 14,79 ⇒ c ≈ 29,58
b
h
sin α =
⇒ h = sin65°⋅ 35 ≈ 31,72
b
2. sin52° =
h
⇒ h = sin52°⋅ 50 ≈ 39,4
50
ε 10
10
3. sin =
⇒e=
≈ 2864,79
2 e
sin0,2
4.
2
⇒ α ≈ 66,42° ⇒ β ≈ 66,42°
5
γ + δ = 360° − 2 ⋅ 66,42° = 227,16° ⇒ γ ≈ 113,58° ⇒ δ ≈ 113,58°
h
sin66,42° =
⇒ h = sin66,42° ⋅ 5 ≈ 4,58°
5
1
Flächeninhalt : A = 2 ⋅ ADreieck + ARe chteck = 2 ⋅ ⋅ 2 ⋅ 4,6 + 6 ⋅ 4,6 ≈ 36,8
2
cosα =
5.
a
a
a2 3
1
a2 = h 2 + ( )2 ⇒ h 2 = a2 − ( )2 = a2 − = a2 ⇒ h = a 3
2
2
4 4
2