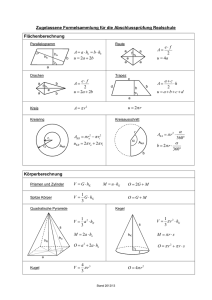
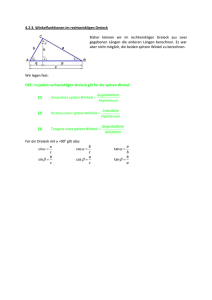
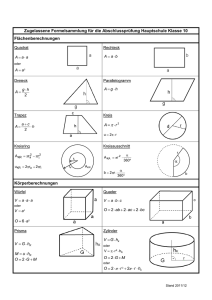
Schulwissen

Schulwissen
Unterstufe:
• Zahlen:
N = {1, 2, 3, 4, . . .},
Z = {. . . , −2, −1, 0, 1, 2, . . .},
Q = nk | k ∈ Z, n ∈ N,
R = Zahlenstrahl
(natürliche)
(ganze)
(rationale)
(reelle)
• Assoziativgesetz:
a + (b + c) = (a + b) + c
und
a(bc) = (ab)c.
• Kommutativgesetz:
a+b=b+a
und
ab = ba.
• Distributivgesetz:
a(b + c) = ab + ac.
• Binomische Formeln:
(a + b)2 = a2 + 2ab + b2 ,
(a − b)2 = a2 − 2ab + b2 ,
(a + b)(a − b) = a2 − b2 .
(1)
(2)
(3)
• Bruchrechnen:
1
x+y
x y
(x + y) =
= + ,
z
z
z z
xy
xy
=
,
ab
ab
ax
x
= .
az
z
• Achtung! Differenzen und Summen kürzen nur die Dummen:
x+y
y
6= .
x+z
z
Mittelstufe:
• Potenzrechnen:
xa xb = xa+b ,
xa y a = (xy)a ,
(xa )b = xab ,
a
1
1
−a
x = a =
.
x
x
• Wurzeln (für x, y > 0):
√
√ √
x y,
√
√
= b xa = ( b x)a .
xy =
xa/b
Achtung! Im allgemeinen ist
√
√
√
x + y 6= x + y.
• Bei Gleichungen der Form
a=b
darf man folgende Äquivalenzumformungen durchführen (das Zeichen
⇔ steht hierbei für ,,äquivalent zu”):
a=b
a=b
⇔
⇔
a + x = b + x,
ax = bx (sofern x 6= 0).
• Die Lösungen der Gleichung
ax2 + bx + c = 0
sind
x1 , x2 = −
b±
√
b2 − 4ac
.
2a
• Satz des Pythagoras: Im Dreieck mit Seitenlängen a, b, c und 90◦ Winkel zwischen den Seiten a, b gilt:
a2 + b 2 = c 2 .
c
b
a
• Im Dreieck mit Seitenlängen a, b, c und 90◦ -Winkel zwischen den Seiten
a, b und Winkel α zwischen den Seiten a, c heißt Seite a die Ankathete,
b die Gegenkathete und c die Hypotenuse.
e
p
c=
Hy
s
nu
e
t
o
b = Gegenkathete
α
a = Ankathete
Es gilt:
cos(α) =
a
Ankathete
=
,
c
Hypotenuse
sin(α) =
b
Gegenkathete
=
,
c
Hypotenuse
tan(α) =
b
Gegenkathete
sin(α)
=
=
.
a
Ankathete
cos(α)
• Am Einheitskreis gilt:
1,5
1
0,5
-2
-1,5
-1
-0,5
0
1
y = sin(α)
α
x = cos(α)
0,5
1
1,5
-0,5
-1
-1,5
Mit Pythagoras folgt:
1 = x2 + y 2 = (cos α)2 + (sin α)2 .
• Allgemeiner:
Die Punkte (x, y) in der xy-Ebene, die auf dem Kreis mit Radius r um
den Ursprung (0, 0) liegen, erfüllen die Gleichung
x2 + y 2 = r 2 .
2