BMT 2013 Lösungen

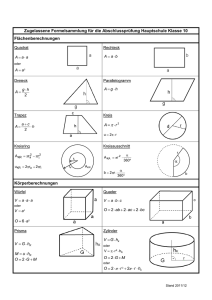
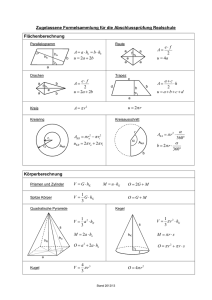
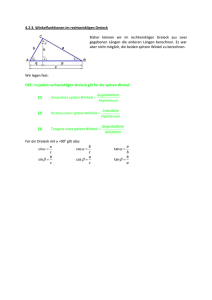
BMT 2013 Gruppe A
1.
Lösung
I x + 2y = 3
II 4x + 5y = 6
Es empfiehlt sich das Einsetzverfahren:
I ⇒
x = 3 − 2y
in II ⇒ 4⋅(3 − 2y) + 5y = 6
⇒
12 − 8y + 5y = 6
⇒
− 3y = − 6 ⇒
y = 2
in I ⇒ x = 3 − 2⋅(2) = − 1
-----------------------------------------------------------------------------------------------------------------2. a) 20% j 40t ⇒ 100% j 200t
b) Masse: 108 ⋅ 20⋅10−3g = 20⋅105 g = 20⋅102 kg
Wert: 20⋅102 ⋅ 40000 € = 20⋅102 ⋅ 4⋅104 € = 80⋅106 € = 80 Millionen Euro
Selbstverständlich lässt sich die Aufgabe auch ohne Verwendung von Zehnerpotenzen
lösen.
-----------------------------------------------------------------------------------------------------------------3. a) Q liegt auf
i) dem Kreis um M mit Radius r
ii) dem Thaleskreis über der Strecke [MP]
2
b) Pythagoras: r2 + PQ = s2
⇒
PQ =
s2 − r2
1
c) ARPQM = 2⋅ ⋅r⋅PQ = r⋅PW´Q
2
d) sinϕ =
Gegenkathete
r
Gegenkathete
r
= und tanϕ =
=
Hypotenuse
s
Ankathete
PQ
Diese beiden Gleichung sind also korrekt.
Ankathete
PQ
und ist nicht angegeben.
=
Hypotenuse
s
-----------------------------------------------------------------------------------------------------------------4. Die Männer dürften eine Größe von 1,80 m haben.
Dagegen ist cosϕ =
Nähert man den Tank durch einen Quader an, dann würde in etwa gelten:
Länge des Tanks: 3 m
Breite des Tanks: 2 m (vgl. Straßenbreite)
Höhe des Tanks : 1 m (vgl. die Größe der Männer)
Volumen: V = 3m ⋅ 2m ⋅ 1m = 6 m3
-----------------------------------------------------------------------------------------------------------------5. a) Strahlensatz:
Verhältnis der Querstrecken = Verhältnis der Abstände entsprecher Endpunkte zum Zentrum
8
5
=
ist korrekt.
x
8−a

8 
b) A(x) = x⋅8 − x = 0 ⇒
5 

x = 0 ∨ 8−
8
x = 0
5
⇒
x = 0 ∨ x = 5
Ein Produkt hat genau dann den Wert Null, wenn (mindestens) ein Faktor den Wert
Null hat.
x- Koordinate des Scheitels: x = 2,5
c) Die x-Koordinate des Scheitels istder Wert von x, für den das Rechteck maximalen
Flächeninhalt hatt.
-----------------------------------------------------------------------------------------------------------------5. a) α = 60°
⇒
Nebenwinkel α∗ = 180° − 60° = 120°
Winkelsumme im gleichschenkligen Dreieck DAC ergibt
δ =
180° − 120°
= 30°
2
b) Analog ergibt sich ε = 40°.
Das Dreieck DEC läss sich als nach WSW aus konstruieren.
Die Punkte A und B erhält durch Antragen der Winkel δ und ε bei C.
Beachte:
Man erhält A und B auch als Schnittpunkte der Mittelsenkrechte von [DC] und [EC].
_________________________________________________________________________