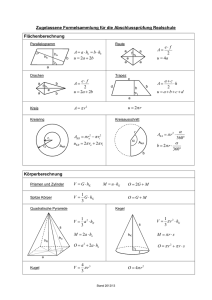
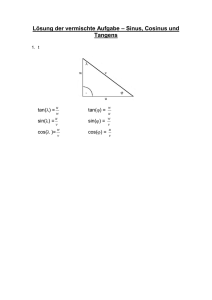
RT 1002 Trigonometrie Grundlagen 1

Übungsaufgaben: Trigonometrie
Gegenkathete
Ankathete
Gegenkathete
COS =
TAN =
Hypotenuse
Hypotenuse
Ankathete
___________________________________________________________________________
SIN =
1.a.
sin α = 0,25
α =
cos α =
tan α =
b.
cos β = 0,67
β =
sin β =
tan β =
c.
tan γ = 1,85
γ =
sin γ =
cos γ =
2. Im rechtwinkligen Dreieck ABC ist der Winkel γ = 90° (an der Ecke C).
a. Beschriftete Zeichnung:
b. Gegeben:
a = 12
c = 20
Gesucht: α, β, hc
c. Gegeben:
b = 9,5
β = 72°
Gesucht: a, hc
3. Im gleichschenkligen Dreieck ABC ist c die Basis und a = b sind die Schenkel.
a. Beschriftete Zeichnung:
b. Gegeben:
a = 6,3
α = 66°
Gesucht: c, γ
c. Gegeben:
c = 7,2
γ = 40°
Gesucht: b, β
4. Im rechtwinkligen Dreieck ABC ist der Winkel γ = 90° (an der Ecke C).
b. Berechne α und β, wenn a = 3,2 cm und c = 5,6 cm.
b. Berechne b und c, wenn a = 4,5 cm und tan α = 1,4
5. Eine Leiter der Länge 7,5 m lehnt in der Höhe 6,6 m an einer Hauswand.
b. Bestimme den Winkel α zwischen Leiter und Fußboden.
c. Wie weit ist das untere Ende von der Hauswand entfernt?
d. Die Leiter wird auf die Hälfte der Wand, d.h. auf 3,3 m, angelegt. Halbiert sich damit
auch der Winkel α?
6. Die Rohrleitung eines Wasserkraftwerks fällt um 360 m. Auf einer Karte 1 : 25 000
misst sie 3,2 cm. Berechne ihren Steigungswinkel und ihre Länge.
7. Welchen Flächeninhalt hat dieses Parallelogramm mit c = 10 cm, d = 8 cm und δ = 60°?
D
δ
c
hd
C
d
b
A
a
B
8. Ein Quader hat die Kanten a = 5 cm, b = 4 cm und c = 3 cm. Berechne die Winkel
α, β und γ, welche die Raumdiagonale mit den Kanten a, b und c bildet.